Section: New Results

Quantum Zeno dynamics

Participants: B. Huard, L. Bretheau, P. Campagne-Ibarcq, F. Mallet.

The results of this section were published in [13] .

Electromagnetic modes are instrumental for realizing quantum physics experiments and building quantum machines. Their manipulation usually involves the tailoring of their Hamiltonian in time. An alternative control scheme, called Quantum Zeno Dynamics (QZD), consists in restricting the evolution of a mode to a subset of possible states. This promising control scheme had been implemented in 2014 on atomic levels of Rb and of a Rydberg atom.

We have made the first observation of QZD of light, using superconducting circuits. By preventing the access to a single energy level, the dynamics of the field is dramatically changed. In this experiment, it was indeed possible to avoid a number of photons $N$, which was arbitrarily chosen between 2 and 5. Under this constraint, and starting in its ground state, a resonantly driven mode is confined to levels 0 to $N-1$. The level occupation is then found to oscillate in time, similarly to an $N$-level system. Performing a direct Wigner tomography of the field reveals its non-classical features. In particular, at half period in the evolution, it resembles a "Schrödinger cat state".

In its original definition, the quantum Zeno effect corresponds to the inhibition of coherent transitions from, or to, the pointer states of a strong measurement or dissipative process. Instead of freezing the dynamics, one can restrict it to a given subspace by choosing a measurement with degenerate eigenvalues.

Similar behavior can also be induced by rapid unitary "kicks", leaving the subspace to protect unaffected. It can be understood considering a model for the original Zeno measurement as a series of coherent interactions with ancillary systems. When the interactions are strong enough, departure from the subspace is perfectly suppressed, so that the outcome of the detector is always the same. Therefore, the ancillas are all left in the same state after the interaction and they do not need to be reset. One can then enforce Zeno dynamics by performing repeatedly unitary operations controlling the state of an auxiliary degree of freedom. This amounts to re-using the same ancilla, at the condition that the unitary evolutions are fast enough to effectively randomize the phase of coherences created with the system. In that sense, QZD is a coherent feedback, which engineers the energy level landscape of a system or its environment by coherent coupling with an ancillary degree of freedom.

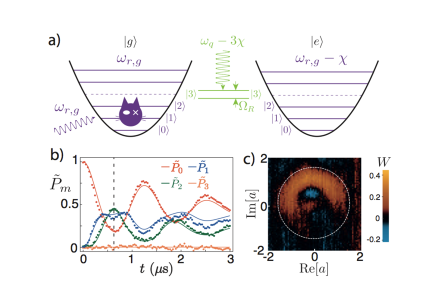
In the experiment, a qubit in the resolved photon number regime plays the role of the ancillary system. A strong Rabi drive is applied on its transition conditioned on the cavity mode hosting $N$ photons ($N$ = 3 on Fig. 7 ). The drive hybridizes the levels $|N,g\rangle$ and $|N,e\rangle$ that repel each other. The level $|N\rangle$ is then moved out from the harmonic ladder of the cavity mode. When starting in the vacuum and applying a coherent drive at ${\omega }_r$, the generated state cannot contain $N$ photons so that it is restricted to $N$ levels.

When measuring the Fock state occupation probabilities as a function of time for this effective driven $N$-level system, characteristic oscillations appear (see Fig. 7 b). Quantum coherence of the field is revealed by direct Wigner tomography (see Fig. 7 c). At half-period of the oscillations, fringes with negativities can be observed. This non classical state is similar to a "Schrödinger cat state", confined in phase space within a circular barrier of radius $\sqrt{N}$.

All these observations are well captured by a model based on $N$ levels only. Our results demonstrate that QZD allows the direct control of the field state in its phase space. This experiment paves the way to the realization of various protocols, such as phase space tweezers, generation and protection of entanglement, and quantum logic operations.