Section: Overall Objectives

Overall Objectives

Computational Biology and Computational Structural Biology. Understanding the lineage between species and the genetic drift of genes and genomes, apprehending the control and feed-back loops governing the behavior of a cell, a tissue, an organ or a body, and inferring the relationship between the structure of biological (macro)-molecules and their functions are amongst the major challenges of modern biology. The investigation of these challenges is supported by three types of data: genomic data, transcription and expression data, and structural data.

Genetic data feature sequences of nucleotides on DNA and RNA molecules, and are symbolic data whose processing falls in the realm of Theoretical Computer Science: dynamic programming, algorithms on texts and strings, graph theory dedicated to phylogenetic problems. Transcription and expression data feature evolving concentrations of molecules (RNAs, proteins, metabolites) over time, and fit in the formalism of discrete and continuous dynamical systems, and of graph theory. The exploration and the modeling of these data are covered by a rapidly expanding research field termed systems biology. Structural data encode informations about the 3D structures of molecules (nucleic acids (DNA, RNA), proteins, small molecules) and their interactions, and come from three main sources: X ray crystallography, NMR spectroscopy, cryo Electron Microscopy. Ultimately, structural data should expand our understanding of how the structure accounts for the function of macro-molecules – one of the central questions in structural biology. This goal actually subsumes two equally difficult challenges, which are folding – the process through which a protein adopts its 3D structure, and docking – the process through which two or several molecules assemble. Folding and docking are driven by non covalent interactions, and for complex systems, are actually inter-twined [48]. Apart from the bio-physical interests raised by these processes, two different application domains are concerned: in fundamental biology, one is primarily interested in understanding the machinery of the cell; in medicine, applications to drug design are developed.

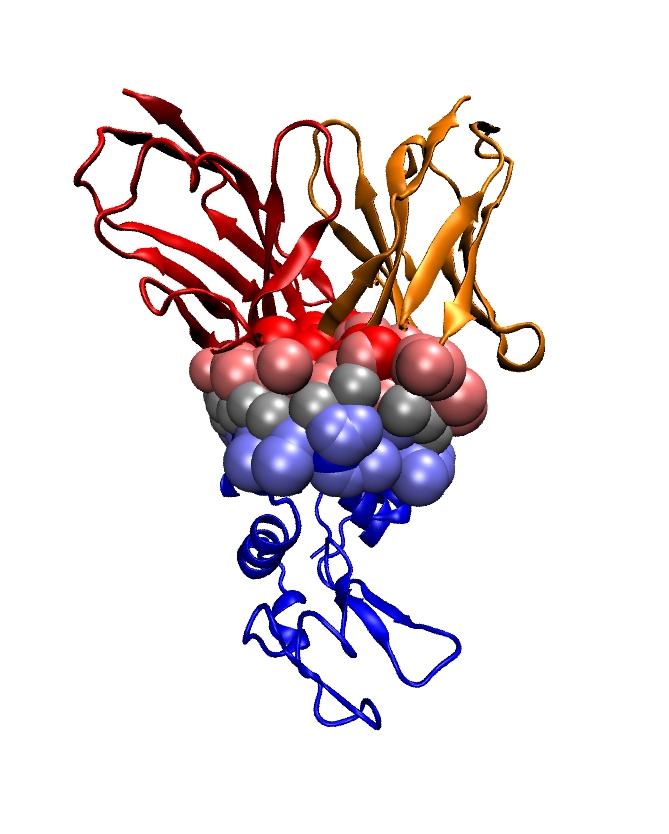
Modeling in Computational Structural Biology. Acquiring structural data is not always possible: NMR is restricted to relatively small molecules; membrane proteins do not crystallize, etc. As a matter of fact, the order of magnitude of the number of genomes sequenced is of the order of one thousand, which results in circa one million of genes recorded in the manually curated Swiss-Prot database. On the other hand, the Protein Data Bank contains circa 90,000 structures. Thus, the paucity of structures with respect to the known number of genes calls for modeling in structural biology, so as to foster our understanding of the structure-to-function relationship.

Ideally, bio-physical models of macro-molecules should resort to quantum mechanics. While this is possible for small systems, say up to 50 atoms, large systems are investigated within the framework of the Born-Oppenheimer approximation which stipulates the nuclei and the electron cloud can be decoupled. Example force fields developed in this realm are AMBER, CHARMM, OPLS. Of particular importance are Van der Waals models, where each atom is modeled by a sphere whose radius depends on the atom chemical type. From an historical perspective, Richards [46], [35] and later Connolly [31], while defining molecular surfaces and developing algorithms to compute them, established the connexions between molecular modeling and geometric constructions. Remarkably, a number of difficult problems (e.g. additively weighted Voronoi diagrams) were touched upon in these early days.

The models developed in this vein are instrumental in investigating the interactions of molecules for which no structural data is available. But such models often fall short from providing complete answers, which we illustrate with the folding problem. On one hand, as the conformations of side-chains belong to discrete sets (the so-called rotamers or rotational isomers) [37], the number of distinct conformations of a poly-peptidic chain is exponential in the number of amino-acids. On the other hand, Nature folds proteins within time scales ranging from milliseconds to hours, while time-steps used in molecular dynamics simulations are of the order of the femto-second, so that biologically relevant time-scales are out reach for simulations. The fact that Nature avoids the exponential trap is known as Levinthal's paradox. The intrinsic difficulty of problems calls for models exploiting several classes of informations. For small systems, ab initio models can be built from first principles. But for more complex systems, homology or template-based models integrating a variable amount of knowledge acquired on similar systems are resorted to.

The variety of approaches developed are illustrated by the two community wide experiments CASP (Critical Assessment of Techniques for Protein Structure Prediction; http://predictioncenter.org) and CAPRI (Critical Assessment of Prediction of Interactions; http://capri.ebi.ac.uk), which allow models and prediction algorithms to be compared to experimentally resolved structures.

As illustrated by the previous discussion, modeling macro-molecules touches upon biology, physics and chemistry, as well as mathematics and computer science. In the following, we present the topics investigated within ABS .