Section: New Results

A Bayesian Framework for Joint Morphometry of Surface and Curve meshes in Multi-Object Complexes

Participants : Pietro Gori [Correspondant] , Olivier Colliot, Linda Marrakchi-Kacem, Yulia Worbe, Alexandre Routier, Cyril Poupon, Andreas Hartmann, Nicholas Ayache, Stanley Durrleman.

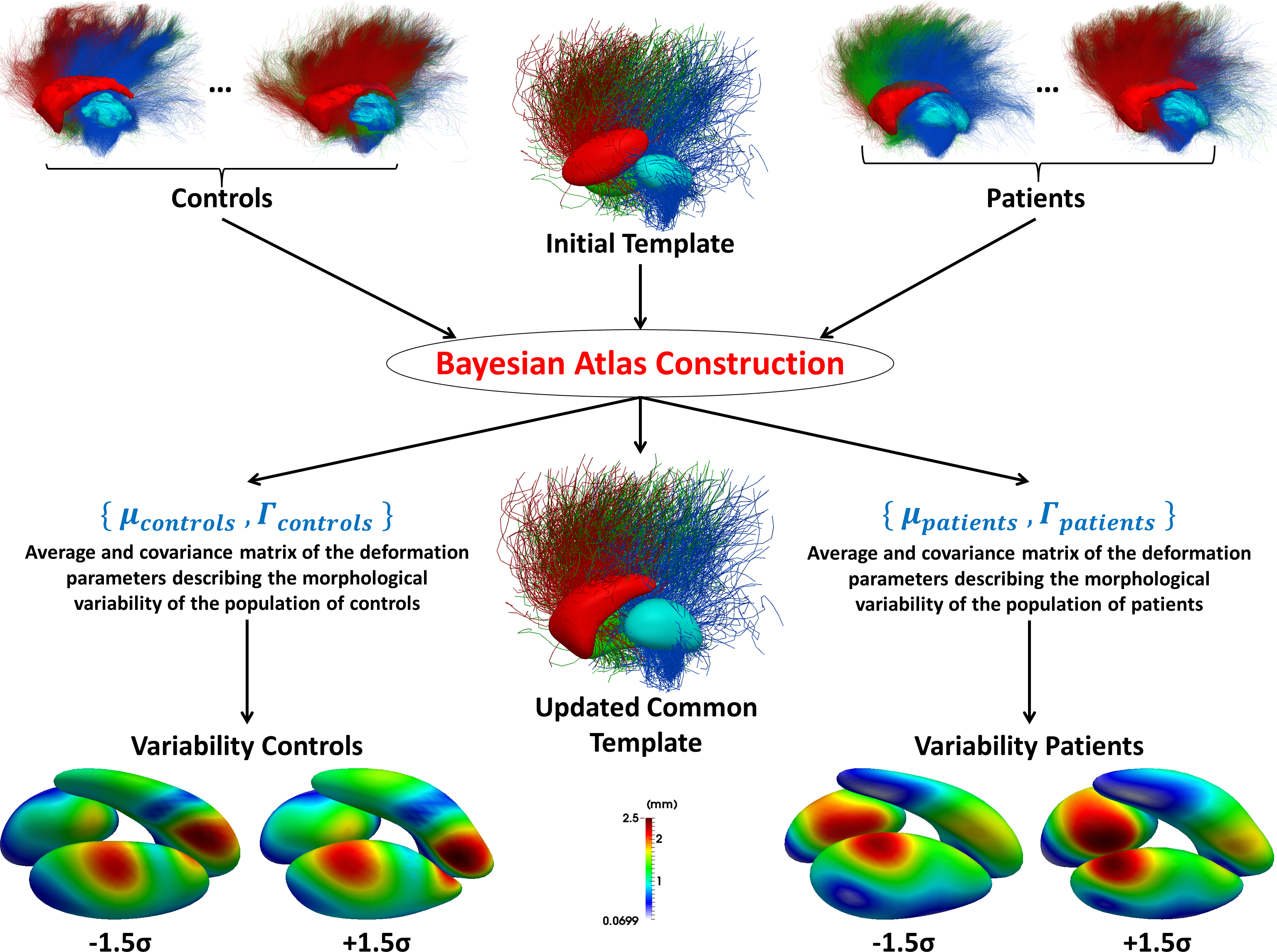
We present a Bayesian framework for atlas construction of multi-object shape complexes comprised of both surface and curve meshes (Figure 1). It is general and can be applied to any parametric deformation framework and to all shape models with which it is possible to define probability density functions (PDF). Here, both curve and surface meshes are modelled as Gaussian random varifolds, using a finite-dimensional approximation space on which PDFs can be defined. Using this framework, we can automatically estimate the parameters balancing data-terms and deformation regularity, which previously required user tuning. Moreover, it is also possible to estimate a well-conditioned covariance matrix of the deformation parameters. We also extend the proposed framework to data-sets with multiple group labels. Groups share the same template and their deformation parameters are modelled with different distributions. We can statistically compare the groups’distributions since they are defined on the same space. We test our algorithm on 20 Gilles de la Tourette patients and 20 control subjects, using three sub-cortical regions and their incident white matter fiber bundles. We compare their morphological characteristics and variations using a single diffeomorphism in the ambient space. The proposed method will be integrated with the Deformetrica software package.

More details in [15].

Figure 1. Bayesian framework for atlas construction of multi-object shape complexes comprised of both surface and curve meshes.