Section: New Results
Fusion of multitemporal and multiresolution remote sensing data and application to natural disasters
Participants : Ihsen Hedhli, Josiane Zerubia [contact] .
This work was carried out in collaboration with Prof. Gabriele Moser and Prof. Sebastiano Serpico from DITEN departement (http://www.dibe.unige.it/index.php?lang=en), University of Genoa, Italy.
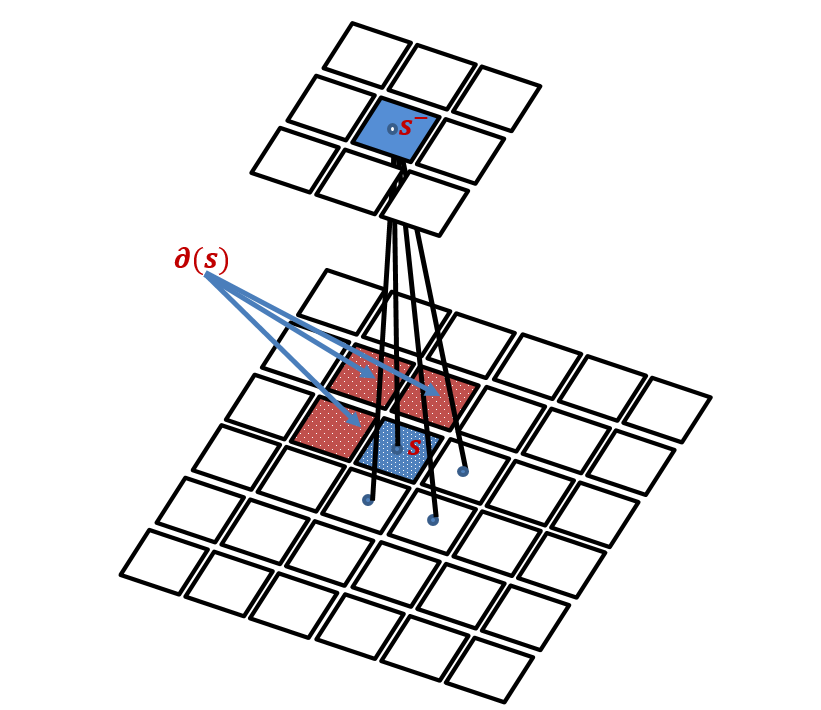
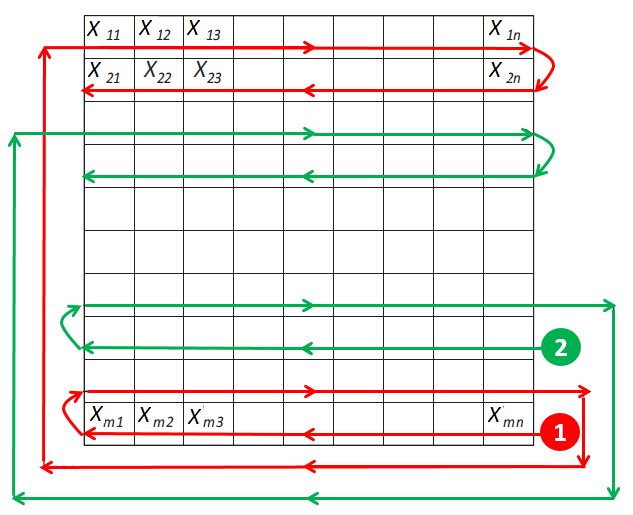
In this work we address the problem of constructing statistical models of images using Hierarchical Hidden Markov modeling techniques for high resolution remotely sensed image classification of urban areas. The main difficulty is to develop a classifier that jointly utilizes the benefits of multi-band and multi-resolution input data while maintaining a good trade-off between accuracy and computation time. In this framework, Markov random field (MRF) models are widely used in classification problems since they provide a convenient and consistent way of integrating contextual information into the classification scheme. Furthermore, MRF models defined according to hierarchical structures exhibit good methodological and application-oriented properties including causality, thanks to the use of appropriate graphs such as a quadtree structure [1]. The input satellite images are inserted in a hierarchical structure on the basis of their spatial resolution. This approach is aimed at both exploiting multi-scale information, which is known to play a crucial role in high-resolution image analysis, and supporting contextual information at each scale. However, hierarchical MRFs on quad-trees rely on a causality concept captured by the factorization of the prior distribution in terms of causal transition probabilities [2]. In practice, this structure tends to generate "blocky" effects in the final classification map. Due to this disadvantage, a new hierarchical MRF based on a Symmetric Markov Mesh Random Field (SMMRF) is proposed in this work, to overcome these limitations from both mathematical and practical points of view, and to establish a causal and symmetrical model. This can be accomplished by scanning the lattice at each level of the hierarchical model based on the visiting scheme shown in Fig 1. Then, for each scale of the quad-tree, the causal SMMRF is integrated into the hierarchical structure. Accordingly, each node at each scale level of the quad-tree, except at the root, is linked to one parent (in the upper level) and three neighbors (in the same level). For each pixel at the root level, there is no parent and only the neighbors remain. The shapes of the neighborhoods of the pixels at the top and left borders of each lattice, at each scale level of the pyramid, are obviously adapted to the image borders [8].
|
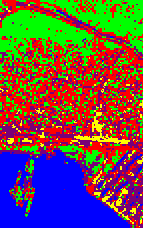
We applied the developed hierarchical classification approach to a multi-resolution dataset that consists of a panchromatic and a multi-spectral Pléiades images acquired over Port-au-Prince (Haiti). Experimental results with HR satellite imagery of a very high-resolution urban scene suggest that the method allows to effectively incorporate spatial information in the hierarchical classification process and provides higher accuracies than previous techniques. Indeed, it is confirmed experimentally (see Fig. 2) that MMRFs and their lattice models are corner-dependent, and that the proposed approach is effective in circumventing this drawback by using a Symmetric Markov Mesh Random Field. The proposed method, in the application to a challenging urban area classification problem, is able to combine the computational and modeling benefits of hierarchical and symmetric mesh MRF models, while preventing their individual artifacts.
|