Section:
New Results
Automatic segmentation of activation periods in an electrogram during atrial fibrillation
Participants: G. Attuel, H. Yahia.
Experiments show that the multiscale properties displayed in signals recording the electrical activity of the heart during (atrial) fibrillation are of the type out of equilibrium dynamics. These dynamics have common features, possibily shared by "subclasses": " power spectrum", large proability laws for the distributions of the amplitude increments, multifractal spectra. Theoretically these dynamics are at least the result of a competition between elastic energies and disorder, which leads to the emergence of collective behaviours. Mathematically, the universality classes involved are not those corresponding to the central limit theorem, but generalize it in its more elaborated forms (Levy & Gnedenko). A class has recently been described completely: directed polymers on a random medium. Scaling exponents are known, together with the fluctuations' statistics. Large deviation theory plays a central role. The fixed point of the associated dynamics is that of KPZ (Kardar-Parisi-Zhang). We have indications that heartbeat dynamics in episodes of atrial fibrillation belongs to that class. In such a context, the questions raised relate to finite size effects when asymptotic convergence is slow. From an experimental point of view, the problem of determining universality classes is very hard. However, it is possible to formulate hypothesis on the universality class so as to extract important information from acquisition signals. A good modus operandi consists in using key properties of a model stated a priori, to combine them with experimental signal analysis in order to produce a posteriori characteristics of interest. Last year, we developed the first model of cardiac dynamics compatible with observed data. The model allows us to test the efficiency of a combined methodology using singularity exponents and Bayesian analysis. This has led us to a first automatic method able to identify periods of cardiac activity and make the distinction with measure noise. From this, the fine automatic determination of activity periods become tractable. This will lead to an automatic quantitative determination of fragmentation, hence opening the way for a determination of universality classes. We illustrate some steps in the figures below.
Figure
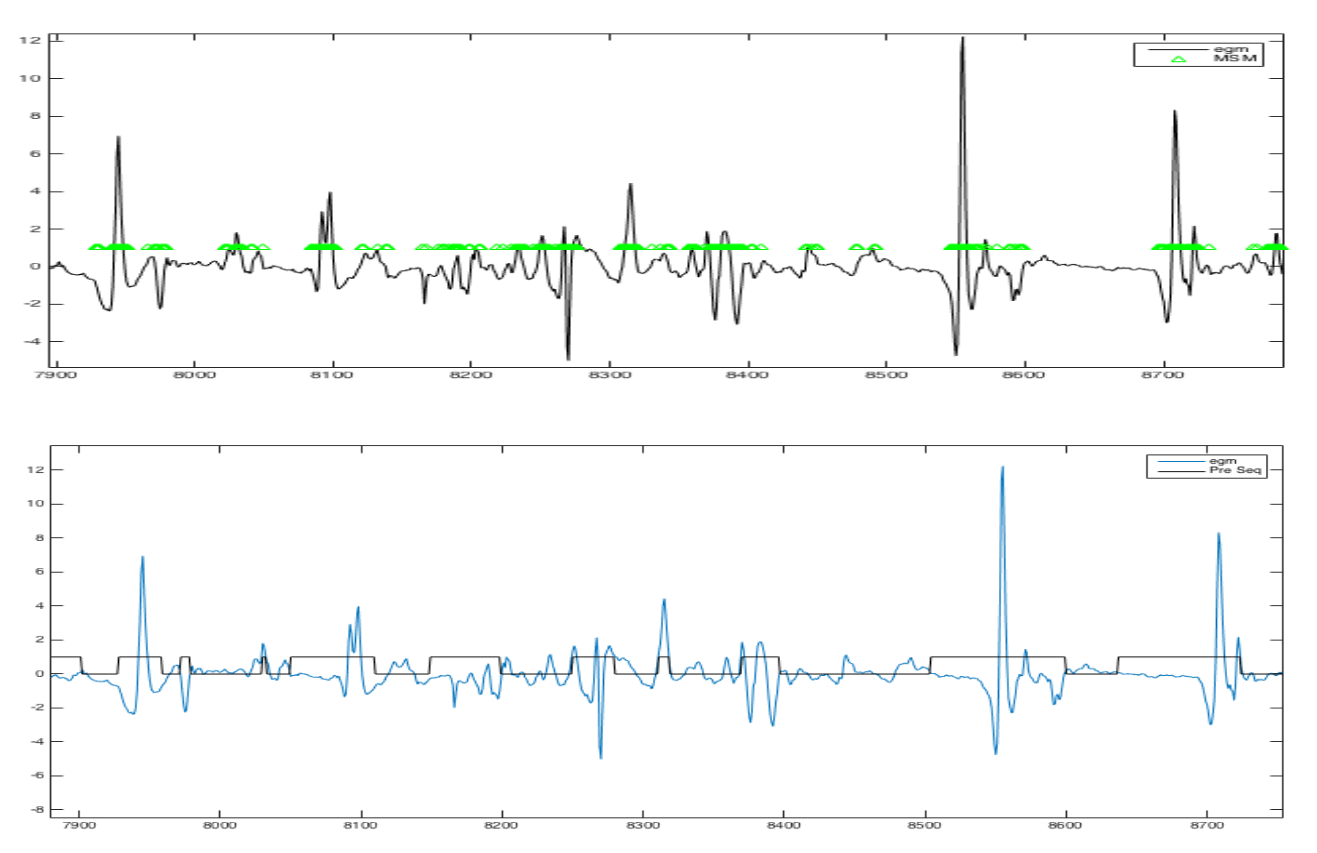
1. Egm during fibrilllation (in black). Density of the most singular manifold (in green). Result of a 2-state HMM (in blue).
|
|
Figure
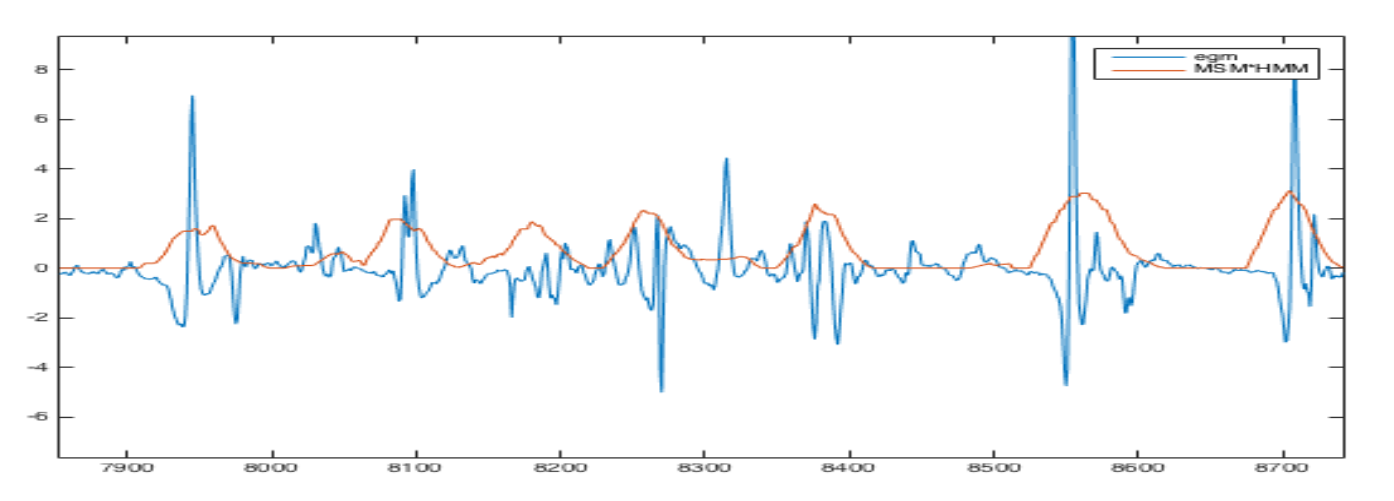
2. Egm during fibrillation (in blue). Signal of activation probability computed with the result of an HMM and the singularity density (in red).
|
|
Figure
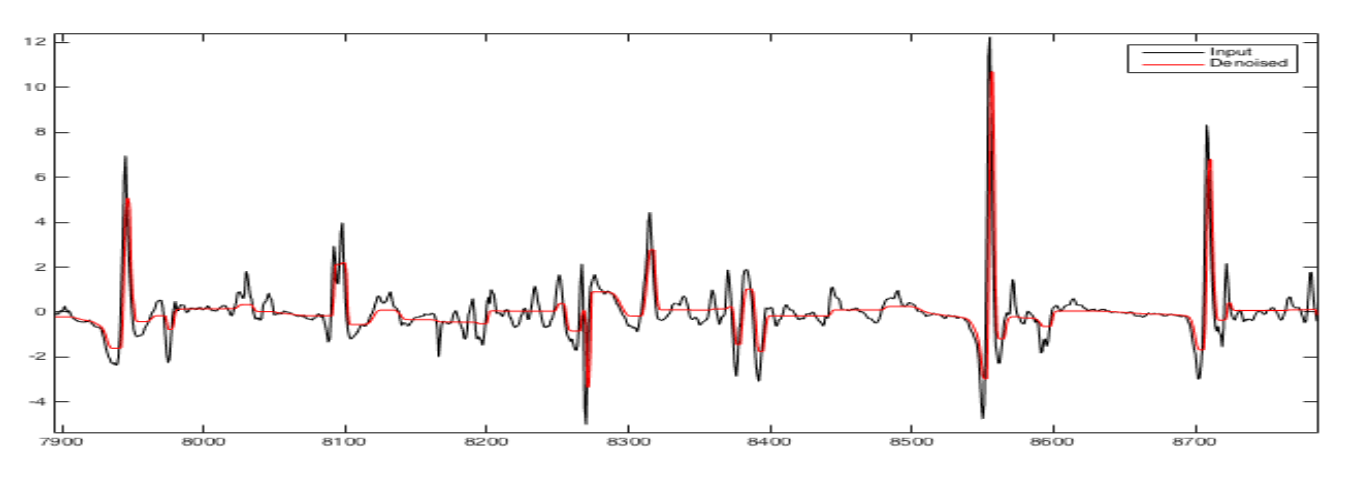
3. Egm during fibrillation (in black). Signal denosised (norm ) (in red).
|
|
Figure
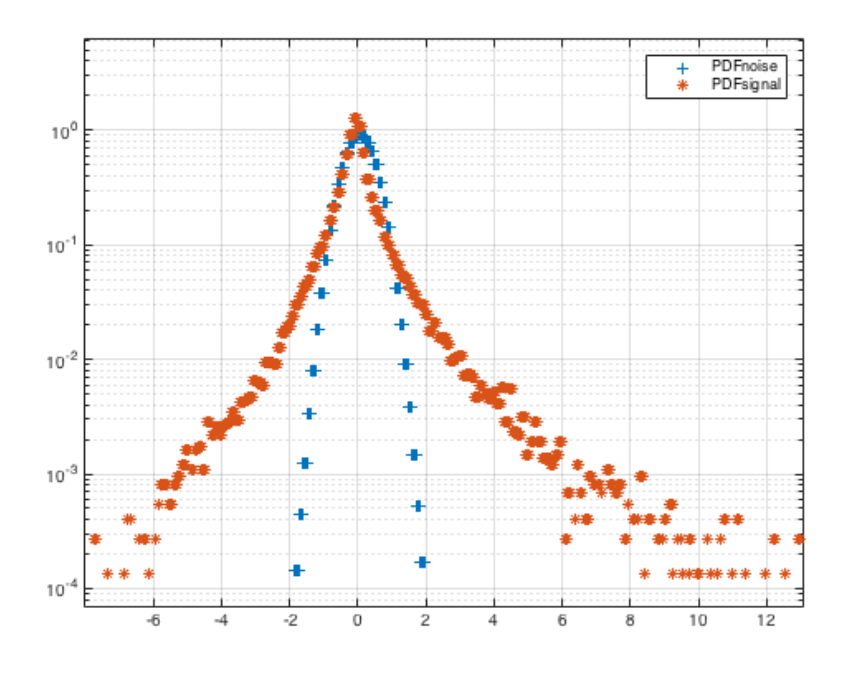
4. Probability distribution of estimated noise (in blue). Distribution of estimated active dynamics (in red).
|
|
Figure
5. Snapshot of the software (written partially in Matlab and which makes use of FluidExponents). The image shows the result of sequencing, with average confidence level, of a real egm
|
|
Publications: [24], [23], [25]