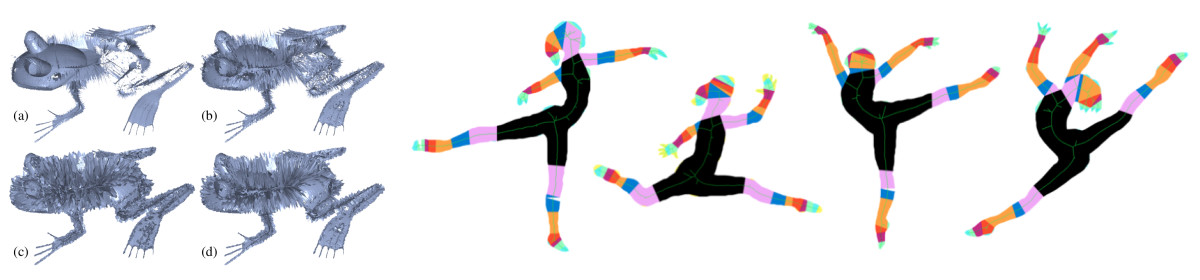Section: New Results
User-centered Models for Shapes and Shape Assemblies
Our goal, is to develop responsive shape models, i.e. 3D models that respond in the expected way under any user action, by maintaining specific application-dependent constraints (such as a volumetric objects keeping their volume when bent, or cloth-like surfaces remaining developable during deformation, etc). We are extending this approach to composite objects made of distributions and/or combination of sub-shapes of various dimensions.
Shape analysis
|
Within the post-doc of Thomas Delame a comparative study between 3D skeletonization methods has been achieved. This work has been summarized as a Eurographics State of the Art [15]. Moreover, a comparative study of the quality between 3D medial axis was assessed and published in Vision, Modeling and Visualization [21].
We developed a multilevel analysis method of 2D shapes and used it to find similarities between the different parts of a shape [22]. Such an analysis is important for many applications such as shape comparison, editing, and compression. Our robust and stable method decomposes a shape into parts, determines a parts hierarchy, and measures similarity between parts based on a salience measure on the medial axis, the Weighted Extended Distance Function, providing a multi-resolution partition of the shape that is stable across scale and articulation. Comparison with our extensive user study on the MPEG-7 database, see below, demonstrates that our geometric results are consistent with user perception. This work has been accomplished within a collaboration between S. Hahmann, Kathryn Leonard (CSUCI), and Geraldine Morin and Axel Carlier (IRIT, ENSEEIHT). K. Leonard was visiting the Imagine team during several month in 2016 as an invited professor funded by the ERC Expressive grant.
We also conducted a large user-study and made the results available throughout an open access data base: The 2D Shape Structure database [9] is a public, user-generated dataset of 2D shape decompositions into a hierarchy of shape parts with geometric relationships retained. It is the outcome of a large-scale user study obtained by crowdsourcing, involving over 1200 shapes in 70 shape classes, and 2861 participants. A total of 41953 annotations has been collected with at least 24 annotations per shape. For each shape, user decompositions into main shape, one or more levels of parts, and a level of details are available. This database reinforces a philosophy that understanding shape structure as a whole, rather than in the separated categories of parts decomposition, parts hierarchy, and analysis of relationships between parts, is crucial for full shape understanding. We provide initial statistical explorations of the data to determine representative (“mean”) shape annotations and to determine the number of modes in the annotations. The primary goal of this work is to make this rich and complex database openly available (through the website http://2dshapesstructure.github.io), providing the shape community with a ground truth of human perception of holistic shape structure. This paper has received the « Reproducibility Award » (http://www.reproducibilitystamp.com).
Surface design
|
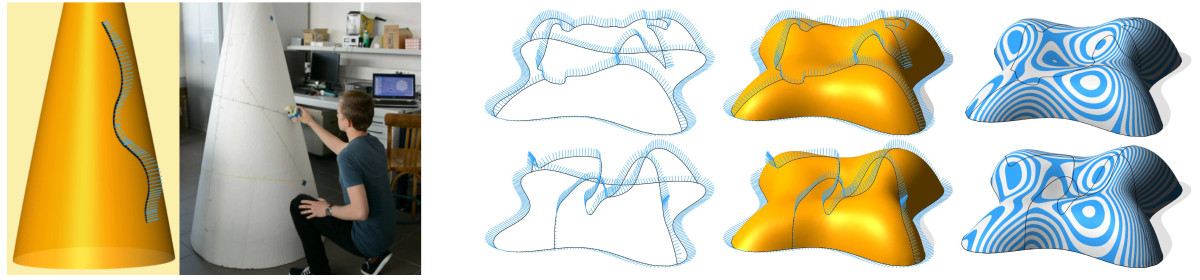
Recent surface acquisition technologies based on micro-sensors produce three-space tangential curve data which can be transformed into a network of space curves with surface normals. In the thesis of Tibor Stanko, which is funded by the CEA-LETI, we dispose such a mobile device equipped with several micro-sensors. The goal of the thesis is to develop surface acquisitions methods using this equipped mobile device. As a first step, we address the theoretical and algorithmic problem of surfacing an arbitrary closed 3D curve network with given surface normals. Thanks to the normal vector input, the patch finding problem can be solved unambiguously and an initial piecewise smooth triangle mesh is computed. The input normals are propagated throughout the mesh. Together with the initial mesh, the propagated normals are used to compute mean curvature vectors. We then compute the final mesh as the solution of a new variational optimization method based on the mean curvature vectors. The intuition behind this original approach is to guide the standard Laplacian-based variational methods by the curvature information extracted from the input normals. The normal input increases shape fidelity and allows to achieve globally smooth and visually pleasing shapes. This work has been presented at Eurographics 2016 as a short paper [25] and GTMG 2016 [26] and has been published as a journal paper [14].
|
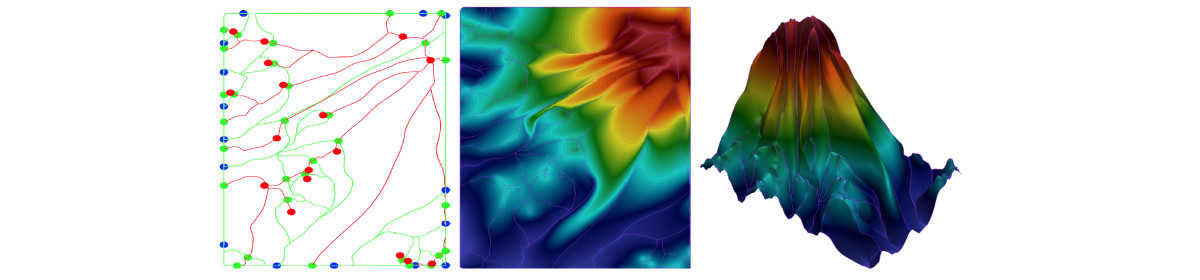
Morse-Smale complexes have been proposed to visualize topological features of scalar fields defined on manifold domains. Herein, three main problems have been addressed in the past: (a) efficient computation of the initial combinatorial structure connecting the critical points; (b) simplification of these combinatorial structures; (c) reconstruction of a scalar field in accordance to the simplified Morse-Smale complex. The PhD thesis of Leo Allemand-Giorgis faces the third problem by proposing a novel approach for computing a scalar field coherent with a given simplified MS complex that privileges the use of piecewise polynomial functions [31]. Based on techniques borrowed from shape preserving design in Computer Aided Geometric Design, our method constructs the surface cell by cell using piecewise polynomial curves and surfaces.