Section: Research Program
Axis 1: Tumor modeling for patient-specific simulations
The gold standard treatment for most cancers is surgery. In the case where total resection of the tumor is possible, the patient often benefits from an adjuvant therapy (radiotherapy, chemotherapy, targeted therapy or a combination of them) in order to eliminate the potentially remaining cells that may not be visible. In this case personalized modeling of tumor growth is useless and statistical modeling will be able to quantify the risk of relapse, the mean progression-free survival time...However if total resection is not possible or if metastases emerge from distant sites, clinicians will try to control the disease for as long as possible. A wide set of tools are available. Clinicians may treat the disease by physical interventions (radiofrequency ablation, cryoablation, radiotherapy, electroporation, focalized ultrasound,...) or chemical agents (chemotherapies, targeted therapies, antiangiogenic drugs, immunotherapies, hormonotherapies). One can also decide to monitor the patient without any treatment (this is the case for slowly growing tumors like some metastases to the lung, some lymphomas or for some low grade glioma). A reliable patient-specific model of tumor evolution with or without therapy may have different uses:
-
Case without treatment: the evaluation of the growth of the tumor would offer a useful indication for the time at which the tumor will reach a critical size. For example, radiofrequency ablation of pulmonary lesion is very efficient as long as the diameter of the lesion is smaller than 3 cm. Thus, the prediction can help the clinician plan the intervention. For slowly growing tumors, quantitative modeling can also help to decide at what time interval the patient has to undergo a CT-scan. CT-scans are irradiative exams and there is a challenge for decreasing their occurrence for each patient. It has also an economical impact. And if the disease evolution starts to differ from the forecast, this might mean that some events have occurred at the biological level. For instance, it could be the rise of an aggressive phenotype or cells that leave a dormancy state. This kind of events cannot be predicted, but some mismatch with respect to the prediction can be an indirect proof of their existence. It could be an indication for the clinician to start a treatment.
-
Case with treatment: a model can help to understand and to quantify the final outcome of a treatment using the early response. It can help for a redefinition of the treatment planning. Modeling can also help to anticipate the relapse by analyzing some functional aspects of the tumor. Again, a deviation with respect to reference curves can mean a lack of efficiency of the therapy or a relapse. Moreover, for a long time, the response to a treatment has been quantified by the RECIST criteria which consists in (roughly speaking) measuring the diameters of the largest tumor of the patient, as it is seen on a CT-scan. This criteria is still widely used and was quite efficient for chemotherapies and radiotherapies that induce a decrease of the size of the lesion. However, with the systematic use of targeted therapies and anti-angiogenic drugs that modify the physiology of the tumor, the size may remain unchanged even if the drug is efficient and deeply modifies the tumor behavior. One better way to estimate this effect could be to use functional imaging (Pet-scan, perfusion or diffusion MRI, ...), a model can then be used to exploit the data and to understand in what extent the therapy is efficient.
-
Optimization: currently, we do not believe that we can optimize a particular treatment in terms of distribution of doses, number, planning with the model that we will develop in a medium term perspective. But it is an aspect that we keep in mind on a long term one.
The scientific challenge is therefore as follows: knowing the history of the patient, the nature of the primitive tumor, its histopathology, knowing the treatments that patients have undergone, knowing some biological facts on the tumor and having a sequence of images (CT-scan, MRI, PET or a mix of them), are we able to provide a numerical simulation of the extension of the tumor and of its metabolism that fits as best as possible with the data (CT-scans or functional data) and that is predictive in order to address the clinical cases described above?
Our approach relies on the elaboration of PDE models and their parametrization with the image by coupling deterministic and stochastic methods. The PDE models rely on the description of the dynamics of cell populations. The number of populations depends on the pathology. For example, for glioblastoma, one needs to use proliferative cells, invasive cells, quiescent cells as well as necrotic tissues to be able to reproduce realistic behaviors of the disease. In order to describe the relapse for hepatic metastases of gastro-intestinal stromal tumor (gist), one needs three cell populations: proliferative cells, healthy tissue and necrotic tissue.
The law of proliferation is often coupled with a model for the angiogenesis. However such models of angiogenesis involve too many non measurable parameters to be used with real clinical data and therefore one has to use simplified or even simplistic versions. The law of proliferation often mimics the existence of an hypoxia threshold, it consists of an O.D.E. or a P.D.E that describes the evolution of the growth rate as a combination of sigmoid functions of nutrients or roughly speaking oxygen concentration. Usually, several laws are available for a given pathology since at this level, there are no quantitative argument to choose a particular one.
The velocity of the tumor growth differs depending on the nature of the tumor. For metastases, we will derive the velocity thanks to Darcy's law in order to express that the extension of the tumor is basically due to the increase of volume. This gives a sharp interface between the metastasis and the surrounding healthy tissues, as observed by anatomopathologists. For primitive tumors like glioma or lung cancer, we use reaction-diffusion equations in order to describe the invasive aspects of such primitive tumors.
The modeling of the drugs depends on the nature of the drug: for chemotherapies, a death term can be added into the equations of the population of cells, while antiangiogenic drugs have to be introduced in a angiogenic model. Resistance to treatment can be described either by several populations of cells or with non-constant growth or death rates. As said before, it is still currently difficult to model the changes of phenotype or mutations, we therefore propose to investigate this kind of phenomena by looking at deviations of the numerical simulations compared to the medical observations.
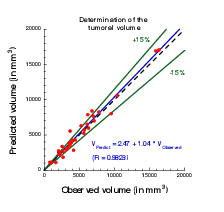
The calibration of the model is achieved by using a series (at least 2) of images of the same patient and by minimizing a cost function. The cost function contains at least the difference between the volume of the tumor that is measured on the images with the computed one. It also contains elements on the geometry, on the necrosis and any information that can be obtained through the medical images. We will pay special attention to functional imaging (PET, perfusion and diffusion MRI). The inverse problem is solved using a gradient method coupled with some Monte-Carlo type algorithm. If a large number of similar cases is available, one can imagine to use statistical algorithms like random forests to use some non quantitative data like the gender, the age, the origin of the primitive tumor...for example for choosing the model for the growth rate for a patient using this population knowledge (and then to fully adapt the model to the patient by calibrating this particular model on patient data) or for having a better initial estimation of the modeling parameters. We have obtained several preliminary results concerning lung metastases including treatments and for metastases to the liver.
|