Section: Research Program
Deductive Program Verification
Permanent researchers: A. Charguéraud, S. Conchon, J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich
The Why3 Ecosystem
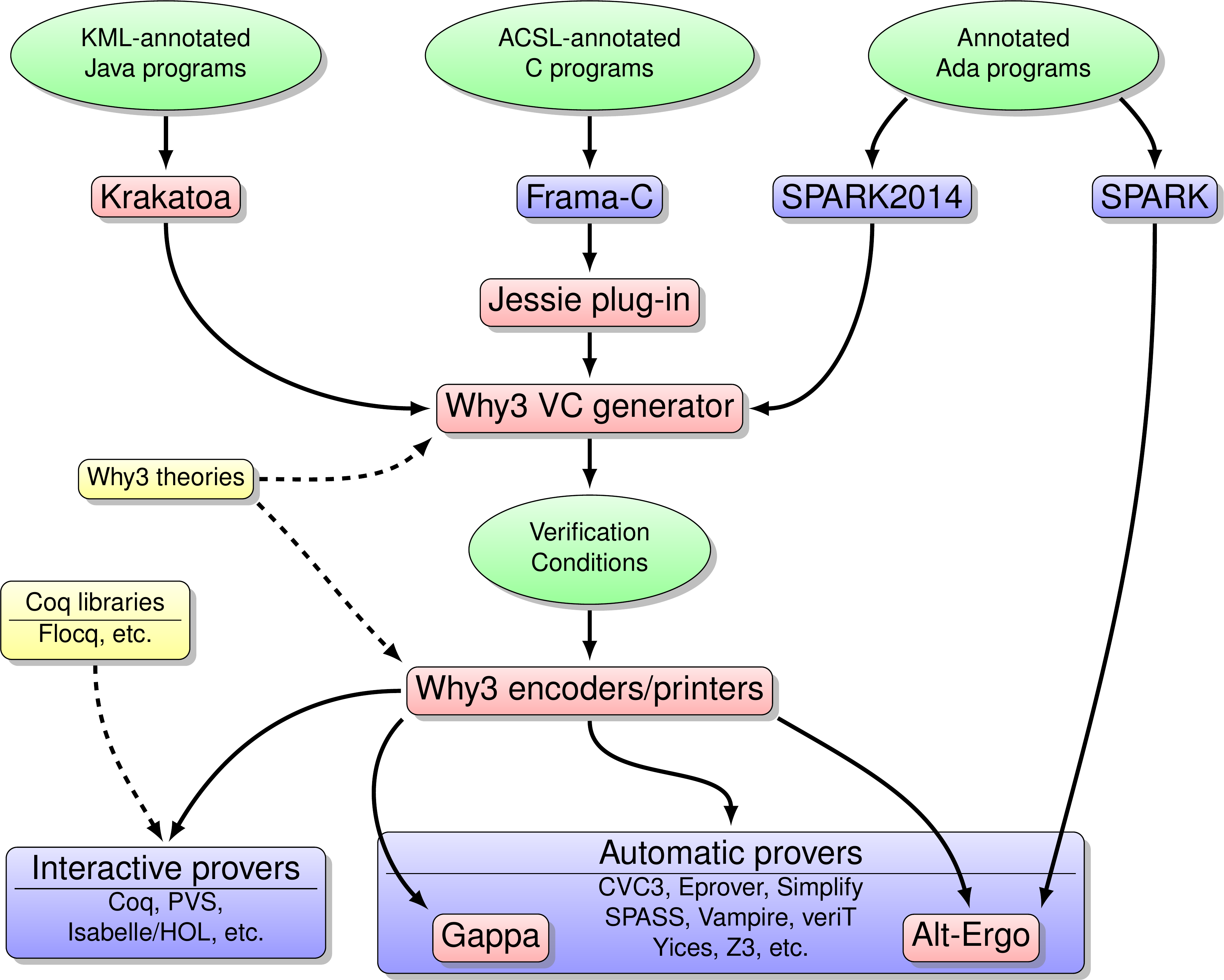
This ecosystem is central in our work; it is displayed on Figure 1. The boxes in red background correspond to the tools we develop in the Toccata team.
-
The initial design of Why3 was presented in 2012 [49], [89]. In the past years, the main improvements concern the specification language (such as support for higher-order logic functions [67]) and the support for provers. Several new interactive provers are now supported: PVS 6 (used at NASA), Isabelle2014 (planned to be used in the context of Ada program via Spark), and Mathematica. We also added support for new automated provers: CVC4, Metitarski, Metis, Beagle, Princess, and Yices2. More technical improvements are the design of a Coq tactic to call provers via Why3 from Coq, and the design of a proof session mechanism [48]. Why3 was presented during several invited talks [88], [87], [84], [85].
-
At the level of the C front-end of Why3 (via Frama-C), we have proposed an approach to add a notion of refinement on C programs [117], and an approach to reason about pointer programs with a standard logic, via separation predicates[47]
-
The Ada front-end of Why3 has mainly been developed during the past three years, leading to the release of SPARK2014 [95] (http://www.spark-2014.org/)
-
In collaboration with J. Almeida, M. Barbosa, J. Pinto, and B. Vieira (University do Minho, Braga, Portugal), J.-C. Filliâtre has developed a method for certifying programs involving cryptographic methods. It uses Why as an intermediate language [40].
-
With M. Pereira and S. Melo de Sousa (Universidade da Beira Interior, Covilhã, Portugal), J.-C. Filliâtre has developed an environment for proving ARM assembly code. It uses Why3 as an intermediate VC generator. It was presented at the Inforum conference [114] (best student paper).
Concurrent Programming
-
S. Conchon and A. Mebsout, in collaboration with F. Zaïdi (VALS team, LRI), A. Goel and S. Krstić (Strategic Cad Labs, INTEL) have proposed a new model-checking approach for verifying safety properties of array-based systems. This is a syntactically restricted class of parametrized transition systems with states represented as arrays indexed by an arbitrary number of processes. Cache coherence protocols and mutual exclusion algorithms are typical examples of such systems. It was first presented at CAV 2012 [7] and detailed further [77]. It was applied to the verification of programs with fences [73]. The core algorithm has been extended with a mechanism for inferring invariants. This new algorithm, called BRAB, is able to automatically infer invariants strong enough to prove industrial cache coherence protocols. BRAB computes over-approximations of backward reachable states that are checked to be unreachable in a finite instance of the system. These approximations (candidate invariants) are then model-checked together with the original safety properties. Completeness of the approach is ensured by a mechanism for backtracking on spurious traces introduced by too coarse approximations [74], [106].
-
In the context of the ERC DeepSea project (Arthur Charguéraud is involved 40% of his time in the ERC DeepSea project, which is hosted at Inria Paris Rocquencourt (team Gallium).), A. Charguéraud and his co-authors have developed a unifying semantics for various different paradigms of parallel computing (fork-join, async-finish, and futures), and published a conference paper describing this work [16]. Besides, A. Charguéraud and his co-authors have polished their previous work on granularity control for parallel algorithms using user-provided complexity functions, and produced a journal article [11].
Case Studies
-
To provide an easy access to the case studies that we develop using Why3 and its front-ends, we have published a gallery of verified programs on our web page http://toccata.lri.fr/gallery/. Part of these examples are the solutions to the competitions VerifyThis 2011 [63], VerifyThis 2012 [3], and the competition VScomp 2011 [90].
-
Other case studies that led to publications are the design of a library of data-structures based on AVLs [66], and the verification a two-lines C program (solving the -queens puzzle) using Why3 [86].
-
A. Charguéraud, with F. Pottier (Inria Paris), extended their formalization of the correctness and asympotic complexity of the classic Union Find data structure, which features the bound expressed in terms of the inverse Ackermann function [39]. The proof, conducted using CFML extended with time credits, was refined using a slightly more complex potential function, allowing to derive a simpler and richer interface for the data structure. A journal article is in preparation.
For other case studies, see also sections of numerical programs and formalization of languages and tools.
Project-team Positioning
Several research groups in the world develop their own approaches, techniques, and tools for deductive verification. With respect to all these related approaches and tools, our originality is our will to use more sophisticated specification languages (with inductive definitions, higher-order features and such) and the ability to use a large set of various theorem provers, including the use of interactive theorem proving to deal with complex functional properties.
-
The RiSE team (http://research.microsoft.com/en-us/groups/rise/default.aspx) at Microsoft Research Redmond, USA, partly in collaboration with team “programming methodology” team (http://www.pm.inf.ethz.ch/) at ETH Zurich develop tools that are closely related to ours: Boogie and Dafny are direct competitors of Why3, VCC is a direct competitor of Frama-C/Jessie.
-
The KeY project (http://www.key-project.org/) (several teams, mainly at Karlsruhe and Darmstadt, Germany, and Göteborg, Sweden) develops the KeY tool for Java program verification [38], based on dynamic logic, and has several industrial users. They use a specific modal logic (dynamic logic) for modeling programs, whereas we use standard logic, so as to be able to use off-the-shelf automated provers.
-
The “software engineering” group at Augsburg, Germany, develops the KIV system (http://www.isse.uni-augsburg.de/en/software/kiv/), which was created more than 20 years ago (1992) and is still well maintained and efficient. It provides a semi-interactive proof environment based on algebraic-style specifications, and is able to deal with several kinds of imperative style programs. They have a significant industrial impact.
-
The VeriFast system (http://people.cs.kuleuven.be/~bart.jacobs/verifast/) aims at verifying C programs specified in Separation Logic. It is developed at the Katholic University at Leuven, Belgium. We do not usually use separation logic (so as to use off-the-shelf provers) but alternative approaches (e.g. static memory separation analysis).
-
The Mobius Program Verification Environment (http://kindsoftware.com/products/opensource/Mobius/) is a joint effort for the verification of Java source annotated with JML, combining static analysis and runtime checking. The tool ESC/Java2 (http://kindsoftware.com/products/opensource/ESCJava2/) is a VC generator similar to Krakatoa, that builds on top of Boogie. It is developed by a community leaded by University of Copenhagen, Denmark. Again, our specificity with respect to them is the consideration of more complex specification languages and interactive theorem proving.
-
The Lab for Automated Reasoning and Analysis (http://lara.epfl.ch/w/) at EPFL, develop methods and tools for verification of Java (Jahob) and Scala (Leon) programs. They share with us the will and the ability to use several provers at the same time.
-
The TLA environment (http://research.microsoft.com/en-us/um/people/lamport/tla/tla.html), developed by Microsoft Research and the Inria team Veridis, aims at the verification of concurrent programs using mathematical specifications, model checking, and interactive or automated theorem proving.
-
The F* project (http://research.microsoft.com/en-us/projects/fstar/), developed by Microsoft Research and the Inria Prosecco team, aims at providing a rich environment for developing programs and proving them.
The KeY and KIV environments mentioned above are partly based on interactive theorem provers. There are other approaches on top of general-purpose proof assistants for proving programs that are not purely functional:
-
The Ynot project (http://ynot.cs.harvard.edu/) is a Coq library for writing imperative programs specified in separation logic. It was developed at Harvard University, until the end of the project in 2010. Ynot had similar goals as CFML, although Ynot requires programs to be written in monadic style inside Coq, whereas CFML applies directly on programs written in OCaml syntax, translating them into logical formulae.
-
Front-ends to Isabelle were developed to deal with simple sequential imperative programs [116] or C programs [113]. The L4-verified project [96] is built on top of Isabelle.