Section:
New Results
User-centered Models for Shapes and Shape Assemblies
-
Scientist in charge: Stefanie Hahmann.
-
Other permanent researchers: Marie-Paule Cani, Frédéric Devernay, Jean-Claude Léon, Damien Rohmer.
Our goal, is to develop responsive shape models, i.e. 3D models that respond in the expected way under any user action, by maintaining specific application-dependent constraints (such as a volumetric objects keeping their volume when bent, or cloth-like surfaces remaining developable during deformation, etc). We are extending this approach to composite objects made of distributions and/or combination of sub-shapes of various dimensions.
Deformation Grammars: Hierarchical Constraint Preservation Under Deformation
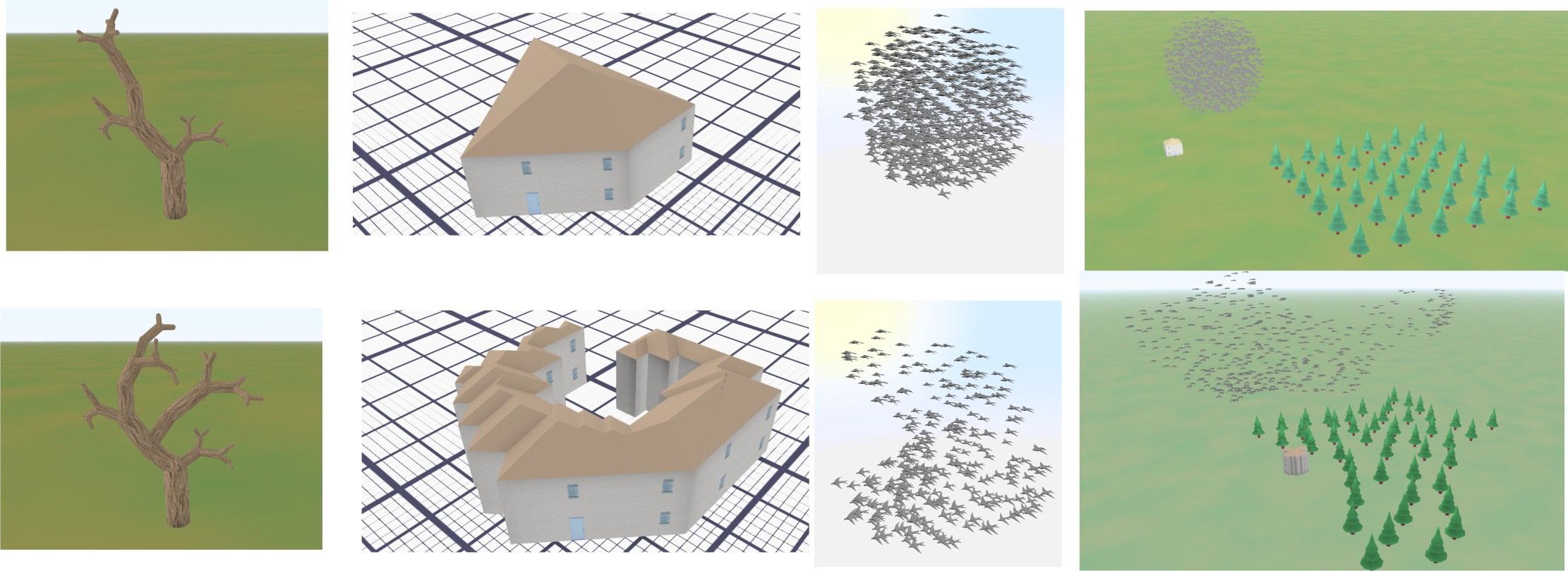
Figure
1. Deformation grammars [25] allow to freely deform complex objects or object assemblies, while preserving their consistency. Top
row: Original hierarchical objects (tree, house, bird flock, scene with mixed elements). The tree and the bird flock are made of parts of the
same type, while the other objects are hetegogeneous hierarchies. Bottom row: Deformed objects, where the interpretation of user-controled
deformations through deformation grammars is used to automatically maintain consistency constraints.
|
|
Deformation grammars are a novel procedural framework enabling to sculpt hierarchical 3D models in an object-dependent manner [25]. They process object deformations as symbols thanks to user-defined interpretation rules. We use them to define hierarchical deformation behaviors tailored for each model, and enabling any sculpting gesture to be interpreted as some adapted constraint-preserving deformation. This is illustrated in Figure 1. A variety of object-specific constraints can be enforced using this framework, such as maintaining distributions of sub-parts, avoiding self-penetrations, or meeting semantic-based user-defined rules. The operations used to maintain constraints are kept transparent to the user, enabling them to focus on their design. We demonstrate the feasibility and the versatility of this approach on a variety of examples, implemented within an interactive sculpting system.
Patterns from Photograph: Reverse-Engineering Developable Products
Figure
2. Patterns from Photograph: Reverse-Engineering Developable Products [17]. Overview of our approach.
(1) Our system takes as input a photograph where the user has traced the object silhouette and the surface patch boundaries.
We also ask users to annotate a global symmetry plane and to indicate symmetric curves. (2) We analyze these annotations to register symmetric curves and to
propagate rulings from the silhouettes towards the interior of the surface patches. The detected symmetric points and rulings provide us with geometric constraints
on the 3D curves, which we express as linear terms in an optimization. (3) Solving this optimization produces a 3D curve network, which we subsequently surface
with developable patches. (4,5) These curves are used as boundaries to generate a piecewise developable mesh of the object.
|
|
Developable materials are ubiquitous in design and manufacturing. Unfortunately, general-purpose modeling tools are not suited to modeling 3D objects composed of developable parts. We propose an interactive tool to model such objects from a photograph [17]. This is illustrated in Figure 2. Users of our system load a single picture of the object they wish to model, which they annotate to indicate silhouettes and part boundaries. Assuming that the object is symmetric, we also ask users to provide a few annotations of symmetric correspondences. The object is then automatically reconstructed in 3D. At the core of our method is an algorithm to infer the 2D projection of rulings of a developable surface from the traced silhouettes and boundaries. We impose that the surface normal is constant along each ruling, which is a necessary property for the surface to be developable. We complement these developability constraints with symmetry constraints to lift the curve network in 3D. In addition to a 3D model, we output 2D patterns enabling to fabricate real prototypes of the object on the photo. This makes our method well suited for reverse engineering products made of leather, bent cardboard or metal sheets.
Defining the Pose of any 3D Rigid Object and an Associated Distance
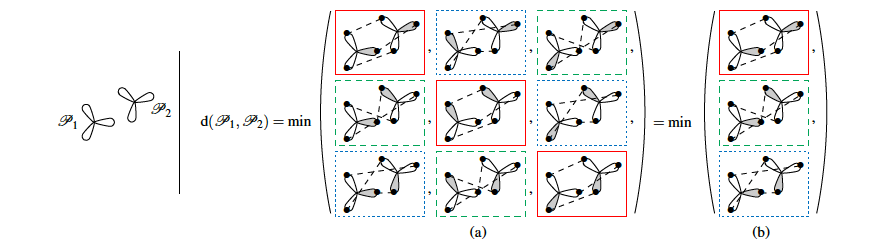
Figure
3. Defining the Pose of any 3D Rigid Object and an Associated Distance [13]. Illustration of our proposed distance for a 2D object with a rotation symmetry of 2p=3. (a) The distance between two poses consists in the minimum distance between two poses of an equivalent object without proper symmetry – here there are 3 possible poses of the equivalent
object for each pose of the original object. The distance between poses of an object without proper symmetry corresponds to the RMS distance
between corresponding object points (dashed segments). (b) Equivalently, the proposed distance can be considered as a measure of the smallest
displacement from one pose to an other – here there are actually only 3 different displacements between those two poses (solid, dotted and dashed boxes).
|
|
The pose of a rigid object is usually regarded as a rigid transformation, described by a translation and a rotation. However, equating the pose space with the space of rigid transformations is in general abusive, as it does not account for objects with proper symmetries – which are common among man-made objects. In our recent work [13], we define pose as a distinguishable static state of an object, and equate a pose with a set of rigid transformations. This is illustrated in Figure 3. Based solely on geometric considerations, we propose a frame-invariant metric on the space of possible poses, valid for any physical rigid object, and requiring no arbitrary tuning. This distance can be evaluated efficiently using a representation of poses within an Euclidean space of at most 12 dimensions depending on the object's symmetries. This makes it possible to efficiently perform neighborhood queries such as radius searches or k-nearest neighbor searches within a large set of poses using off-the-shelf methods. Pose averaging considering this metric can similarly be performed easily, using a projection function from the Euclidean space onto the pose space. The practical value of those theoretical developments is illustrated with an application of pose estimation of instances of a 3D rigid object given an input depth map, via a Mean Shift procedure.