Section: New Results

Electromagnetic wave propagation

Numerical treatment of non-local dispersion for nanoplasmonics

Participants : Stéphane Lanteri, Claire Scheid, Nikolai Schmitt, Jonathan Viquerat.

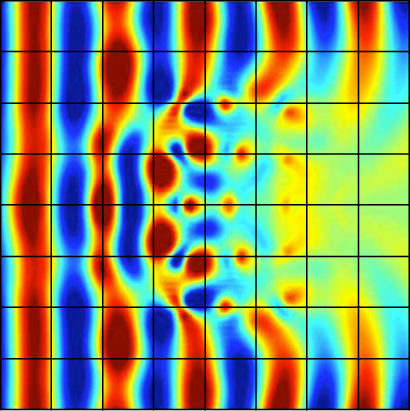
When metallic nanostructures have sub-wavelength sizes and the illuminating frequencies are in the regime of metal's plasma frequency, electron interaction with the exciting fields have to be taken into account. Due to these interactions, plasmonic surface waves can be excited and cause extreme local field enhancements (surface plasmon polariton electromagnetic waves). Exploiting such field enhancements in applications of interest requires a detailed knowledge about the occurring fields which can generally not be obtained analytically. For the numerical modeling of light/matter interaction on the nanoscale, the choice of an appropriate model is a crucial point. Approaches that are adopted in a first instance are based on local (no interaction between electrons) dispersion models e.g. Drude or Drude-Lorentz. From the mathematical point of view, these models lead to an additional ordinary differential equation in time that is coupled to Maxwell's equations. When it comes to very small structures in a regime of 2 nm to 25 nm, non-local effects due to electron collisions have to be taken into account. Non-locality leads to additional, in general non-linear, partial differential equations and is significantly more difficult to treat, though. In this work, we study a DGTD method able to solve the system of Maxwell equations coupled to a linearized non-local dispersion model relevant to nanoplasmonics. This year, we have developed a parallel DGTD solver for the three-dimentional Maxwell equations coupled to a non-local Drude model. Both centered flux-based and upwind flux-based DG schemes have been considered, in combination with with leap-frog and Runge-Kutta time stepping respectively. This is the object of the submitted paper [41]. At the same time, we pursue a study in collaboration with Serge Nicaise (Université de Valenciennes et du Hainaut-Cambresis) on the stability properties of this model both at the continuous and the discrete level.

Numerical modeling of metasurfaces

Participants : Loula Fezoui, Stéphane Lanteri, Liang Li [UESTC, Chengdu, China] , Ronan Perrussel [Laplace laboratory, Toulouse] .

Metamaterials are composed of periodic subwavelength metal/dielectric structures that resonantly couple to the electric and/or magnetic components of the incident electromagnetic fields, exhibiting properties that are not found in nature. Planar metamaterials with subwavelength thickness, or metasurfaces, consisting of a layer of dielectric or plasmonic nanostructures, can be readily fabricated using lithography and nanoprinting methods, and the ultrathin thickness in the wave propagation direction can greatly suppress the undesirable losses. Metasurfaces enable a spatially varying optical response, mold optical wavefronts into shapes that can be designed at will, and facilitate the integration of functional materials to accomplish active control and greatly enhanced nonlinear response. Designing metasurfaces is generally a challenging inverse problem. A recently introduced synthesis techniques is based on so-called General Sheet Transition Conditions (GSTC) that can be leveraged to define the components of general bianisotropic surface susceptibility tensors characterizing the metasurface. A GSTC-based design technique has several advantages: 1) it is exact; 2) it is general, transforming arbitrary incident waves into arbitrary reflected and transmitted waves, 3) it often admits closed-form solutions, 4) it provides deep insight into the physics of the transformations, 5) it allows multiple (at least up to 4) simultaneous and independent transformations. We study the numerical treatment of GSTC in the time-domain and frequency-domain regimes in the DG and HDG settings respectively.

Corner effects in nanoplasmonics

Participants : Camille Carvalho [Applied Mathematics Department, University of California Merced, USA] , Patrick Ciarlet [ENSTA, POEMS project-team] , Claire Scheid.

In this work, we study nanoplasmonic structures with corners (typically a diedral/truangular structure). This is the central subject considered in the PhD thesis of Camille Carvalho. In the latter, the focus is made on a lossles Drude dispersion model with a frequency-domain approach. Several well posedness problems arise due to the presence of corners and are addressed in the PhD thesis. A time-domain approach in this context is also relevant and we propose to use the techniques developed in the team in this prospect. Even if both approaches (time-domain and frequency-domain) represent similar physical phenomena, problems that arise are different. These two approaches appear as complementary; it is thus worth bridging the gap between the two frameworks. We are currently performing a thorough comparison in the case of theses 2D structures with corners and we especially focus on the amplitude principle limit that raises a lot of questions.

Travelling waves for the non-linear Schrödinger equation in 2D

Participants : David Chiron [J.A. Dieudonné Laboratory, Université Nice Sophia Antipolis] , Claire Scheid.

We are interested in the numerical study of the two-dimensional travelling waves of the non-linear Schrödinger equation for a general non-linearity and with nonzero condition at infinity. This equation is appearing in models of nonlinear optics. It has a variational structure that we propose to exploit to design a numerical method. We continue the sudy initiated in [1] and investigate excited states of the Kadomtsev-Petviashvili-I (KP-I) and Gross-Pitaevskii (GP) equations in dimension 2. We address numerically the question of the Morse index of some explicit solutions of KP-I that form a parametrized family of solutions. The results confirm that the lump solitary wave has Morse index one and that the other explicit solutions correspond to excited states. We then turn to the 2D GP equation which in some long wave regime converges to the KP-I equation. We finally perform numerical simulations showing that the other explicit solitary waves solutions to the KP-I equation give rise to new branches of travelling waves of GP corresponding to excited states. This is the object of the submitted paper [37] (currently under a minor revision process).

A structure preserving numerical discretization framework for the Maxwell Klein Gordon equation in 2D.

Participants : Snorre Christiansen [Department of Mathematics, University of Oslo, Norway] , Claire Scheid.

Toward a better understanding of non-linear optical phenomena, we focus on the case of the Maxwell Klein Gordon (MKG) equation in dimension 2. This equation appears in the context of quantum electrodynamics but also in relativity. We propose to develop a numerical discretization framework that takes advantage of the Hamiltonian structure of the equation. The gauge invariance is recovered at the discrete level with the help of the Lattice Gauge theory. We then propose a fully discrete scheme and prove its convergence. The strategy of proof, based on discrete energy principle, is developed in a more general context and next applied in the particular case of MKG equation. This work has been conducted and finalized during a of five month's stay of C. Scheid at the University of Oslo through an invitation in the contexty of the ERC Starting Grant project STUCCOFIELD of S. Christiansen. This work has been presented in 2017 in one conference (see [32] and at the occasion of an invitation for a seminar (see section Invited talks).

Multiscale DG methods for the time-domain Maxwell equations

Participants : Alexis Gobé, Stéphane Lanteri, Raphaël Léger, Diego Paredes Concha [Instituto de Matemáticas, Universidad Católica de Valparaiso, Chile] , Claire Scheid, Frédéric Valentin [LNCC, Petropolis, Brazil] .

Although the DGTD method has already been successfully applied to complex electromagnetic wave propagation problems, its accuracy may seriously deteriorate on coarse meshes when the solution presents multiscale or high contrast features. In other physical contexts, such an issue has led to the concept of multiscale basis functions as a way to overcome such a drawback and allow numerical methods to be accurate on coarse meshes. The present work, which is conducted in the context of the HOMAR Associate Team, is concerned with the study of a particular family of multiscale methods, named Multiscale Hybrid-Mixed (MHM) methods. Initially proposed for fluid flow problems, MHM methods are a consequence of a hybridization procedure which caracterize the unknowns as a direct sum of a coarse (global) solution and the solutions to (local) problems with Neumann boundary conditions driven by the purposely introduced hybrid (dual) variable. As a result, the MHM method becomes a strategy that naturally incorporates multiple scales while providing solutions with high order accuracy for the primal and dual variables. The completely independent local problems are embedded in the upscaling procedure, and computational approximations may be naturally obtained in a parallel computing environment. In this study, a family of MHM methods is proposed for the solution of the time-domain Maxwell equations where the local problems are discretized either with a continuous FE method or a DG method (that can be viewed as a multiscale DGTD method). Preliminary results have been obtained in the two-dimensional case. The corresponding paper submitted at the end of 2016 is currently under revision (preprint available on HAL [14]). This work has also been presented in a conference in 2017, see [33]

HDG methods for the time-domain Maxwell equations

Participants : Alexandra Christophe-Argenvillier [MIT, USA] , Stéphane Descombes, Stéphane Lanteri, Georges Nehmetallah.

This study is concerned with the development of accurate and efficient solution strategies for the system of 3D time-domain Maxwell equations coupled to local dispersion models (e.g. Debye, Drude or Drude-Lorentz models) in the presence of locally refined meshes. Such meshes impose a constraint on the allowable time step for explicit time integration schemes that can be very restrictive for the simulation of 3D problems. We consider here the possibility of using an unconditionally stable implicit time or a locally implicit time integration scheme combined to a HDG discretization method. As a preliminary step, we have investigated a fully explicit HDG method generalizing the classical upwind flux-based DG method for the system of time-domain Maxwell equations. We have study the stability of this new HDG method and in particular, the influence of the stabilization parameter on the CFL condition. We are now assessing the consitions under which we can obtain a superconverging HDG method.

HDG methods for the frequency-domain Maxwell equations

Participants : Stéphane Lanteri, Ludovic Moya.

In the context of the ANR TECSER project, we continue our efforts towards the development of scalable high order HDG methods for the solution of the system of 3D frequency-domain Maxwell equations. We aim at fully exploiting the flexibiity of the HDG discretization framework with regards to the adaptation of the interpolation order ($p$-adaptivity) and the mesh ($h$-adaptivity). In particular, we study the formulation of HDG methods on a locally refined non-conforming tetrahedral mesh and on a non-confoming hybrid cubic/tetrahedral mesh. We also investigate the coupling between the HDG formulation and a BEM (Boundary Element Method) discretization of an integral representation of the electromagnetic field in the case of propagation problems theoretically defined in unbounded domains. The associated methodological contributions are implemented in the HORSE simulation software.

HDG methods for frequency-domain plasmonics

Participants : Stéphane Lanteri, Mostafa Javadzadeh Moghtader, Liang Li [UESTC, Chengdu, China] , Asger Mortensen [DTU Fotonik, Technical University of Denmark] , Martijn Wubs [DTU Fotonik, Technical University of Denmark] .

In this collaboration with physicists at DTU Fotonik, we study HDG methods for solving the frequency-domain Maxwell's equations coupled to the Nonlocal Hydrodynamic Drude (NHD) and Generalized Nonlocal Optical Response (GNOR) models, which are employed to describe the optical properties of nanoplasmonic scatterers and waveguides. The formulations of the HDG method for these two models are exetnsion of our previous works for classical microwave applications. In the present case, two conservativity conditions are globally enforced to make the problem solvable and to guarantee the continuity of the tangential component of the electric field and the normal component of the current density. Numerical results show that the proposed HDG methods converge at optimal rate. These new HDG formulations have been implemented and numerically assessed for two-dimensional problems. Beside, we are also considering the three-dimensional case

Exponential time integrators for a DGTD method

Participants : Stéphane Descombes, Stéphane Lanteri, Bin Li [UESTC, Chengdu, China] , Hao Wang [UESTC, Chengdu, China] , Li Xu [UESTC, Chengdu, China] .

The objective of this study is to design efficient and (high order) accurate time integration strategies for the system of time-domain Maxwell equations discretized in space by a high order discontinuous Galerkin scheme formulated on locally refined unstructured meshes. A new family of implicit-explicit (IMEX) schemes using exponential time integration is developed. The Lawson procedure is applied based on a partitioning of the underlying tetrahedral mesh in coarse and fine parts, allowing the contruction of a time advancing strategy that combines an exact integration of the semi-discrete system for the problem unknowns associated to the elements of the fine part, with an arbitrary high order explicit time integration scheme for the Lawson-transformed system.