Section: Overall Objectives
Presentation
In the Bonus project, the context of optimization, where solving a problem consists in optimizing (minimizing or maximizing) one or more objective function(s) under some constraints, is considered. In this context, a problem can be formulated as follows:
where S is the feasible search space and is the decision variable vector of dimension .
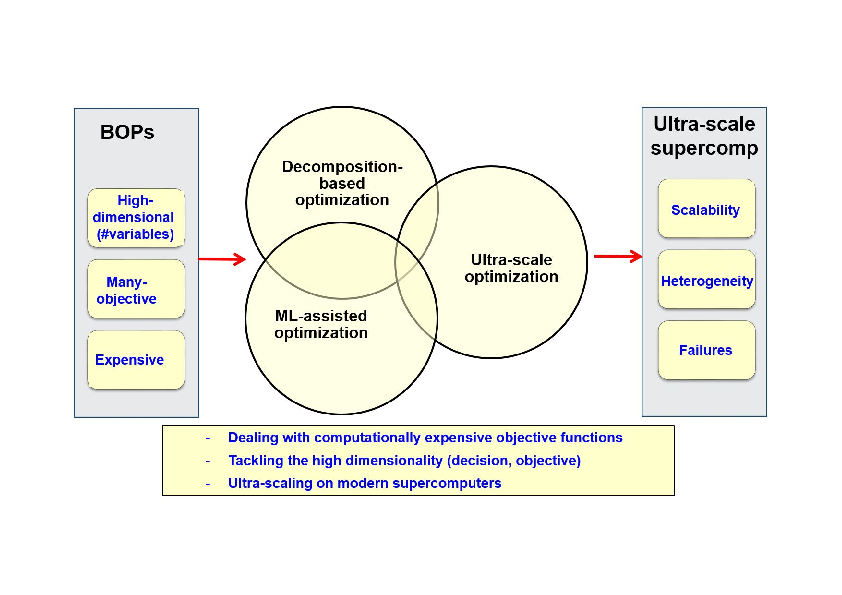
Nowadays, in many research and application areas we are witnessing the emergence of the big era (big data, big graphs, etc). In the optimization setting, the problems are increasingly big in practice. Big optimization problems (BOPs) refer to problems composed of a large number of environmental input parameters and/or decision variables (high dimensionality), and/or many objective functions that may be computationally expensive. For instance, in smart grids, there are many optimization problems for which have to be considered a large number of consumers (appliances, electrical vehicles, etc.) and multiple suppliers with various energy sources. In the area of engineering design, the optimization process must often take into account a large number of parameters from different disciplines. In addition, the evaluation of the objective function(s) often consist(s) in the execution of an expensive simulation of a black-box complex system. This is for instance typically the case in aerodynamics where a CFD-based simulation may require several hours. On the other hand, to meet the high growing needs of applications in terms of computational power in a wide range of areas including optimization, high-performance computing (HPC) technologies have known a revolution during the last decade (see Top500 (Top500 international ranking (Edition of November 2018): https://www.top500.org/lists/2018/11/)). Indeed, HPC is evolving toward ultra-scale supercomputers composed of millions of cores supplied in heterogeneous devices including multi-core processors with various architectures, GPU accelerators and MIC coprocessors.
Beyond the “big buzzword”, solving BOPs raises at least four major challenges: (1) tackling their high dimensionality; (2) handling many objectives; (3) dealing with computationally expensive objective functions; and (4) scaling on (ultra-scale) modern supercomputers. The overall scientific objectives of the Bonus project consist in addressing efficiently these challenges. On the one hand, the focus will be put on the design, analysis and implementation of optimization algorithms scalable to high-dimensional (in decision variables and/or objectives) and/or expensive problems. On the other hand, the focus will also be put on the design of optimization algorithms able to scale on heterogeneous supercomputers including several millions of processing cores. To achieve these objectives raising the associated challenges a program including three lines of research will be adopted (Fig. 1): decomposition-based optimization, Machine Learning (ML)-assisted optimization and ultra-scale optimization. These research lines are developed in the following section.
From the software standpoint, our objective is to integrate the approaches we will develop in our ParadisEO [3] (ParadisEO: http://paradiseo.gforge.inria.fr/) framework in order to allow their reuse inside and outside the Bonus team. The major challenge will be to extend ParadisEO in order to make it more collaborative with other software including machine learning tools, other (exact) solvers and simulators. From application point of view, the focus will be put on two classes of applications: complex scheduling and engineering design.