Section: Research Program

Non-Euclidean computational geometry

Figure 2. Left: 3D mesh of a gyroid (triply periodic surface) [54]. Right: Simulation of a periodic Delaunay triangulation of the hyperbolic plane [24].

Triangulations, in particular Delaunay triangulations, in the Euclidean space ${ℝ}^d$ have been extensively studied throughout the 20th century and they are still a very active research topic. Their mathematical properties are now well understood, many algorithms to construct them have been proposed and analyzed (see the book of Aurenhammer et al. [23]). Some members of Gamble have been contributing to these algorithmic advances (see, e.g. [28], [62], [39], [27]); they have also contributed robust and efficient triangulation packages through the state-of-the-art Computational Geometry Algorithms Library Cgal , (http://www.cgal.org/) whose impact extends far beyond computational geometry. Application fields include particle physics, fluid dynamics, shape matching, image processing, geometry processing, computer graphics, computer vision, shape reconstruction, mesh generation, virtual worlds, geophysics, and medical imaging. (See http://www.cgal.org/projects.html for details.)

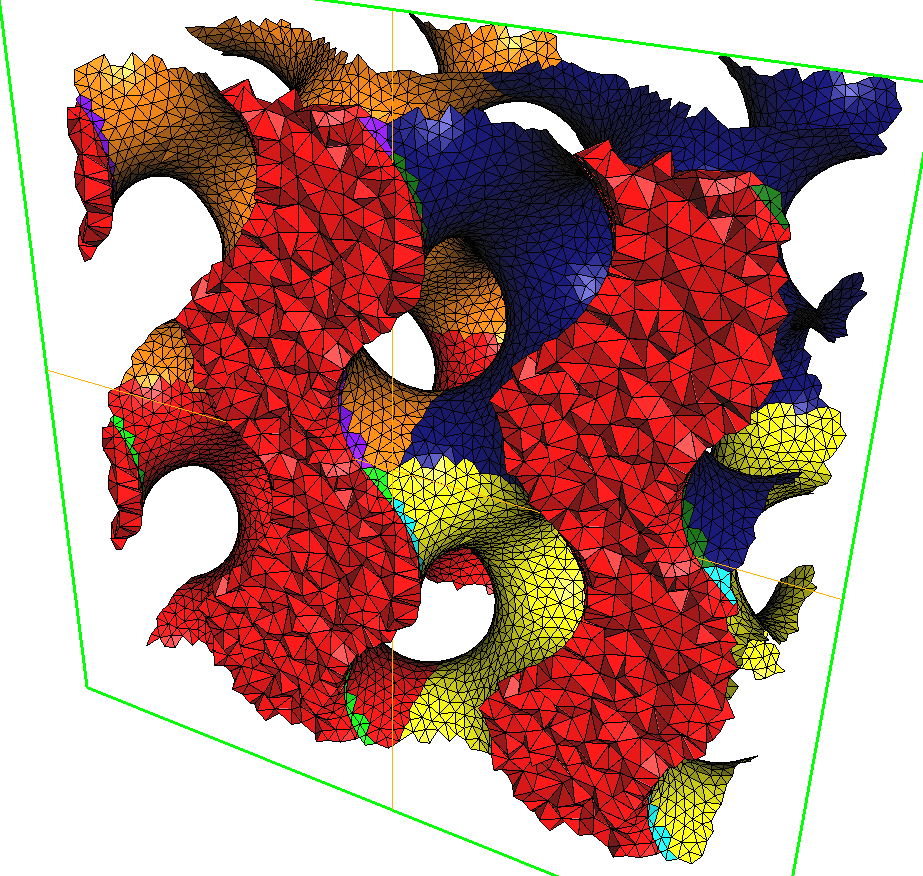
It is fair to say that little has been done on non-Euclidean spaces, in spite of the large number of questions raised by application domains. Needs for simulations or modeling in a variety of domains (See http://www.loria.fr/~teillaud/PeriodicSpacesWorkshop/, http://www.lorentzcenter.nl/lc/web/2009/357/info.php3?wsid=357, http://neg15.loria.fr/ and http://gerdschroeder-turk.org/2015/06/17/shape-up-2015-exercises-in-materials-geometry-and-topology/. ) ranging from the infinitely small (nuclear matter, nano-structures, biological data) to the infinitely large (astrophysics) have led us to consider 3D periodic Delaunay triangulations, which can be seen as Delaunay triangulations in the 3D flat torus, quotient of ${ℝ}^3$ under the action of some group of translations [34]. This work has already yielded a fruitful collaboration with astrophysicists [47], [63] and new collaborations with physicists are emerging. To the best of our knowledge, our Cgal package [33] is the only publicly available software that computes Delaunay triangulations of a 3D flat torus, in the special case where the domain is cubic. This case, although restrictive is already useful. (See examples at http://www.cgal.org/projects.html) We have also generalized this algorithm to the case of general $d$-dimensional compact flat manifolds [35]. As far as non-compact manifolds are concerned, past approaches, limited to the two-dimensional case, have stayed theoretical [53].

Interestingly, even for the simple case of triangulations on the sphere, the software packages that are currently available are far from offering satisfactory solutions in terms of robustness and efficiency [32].

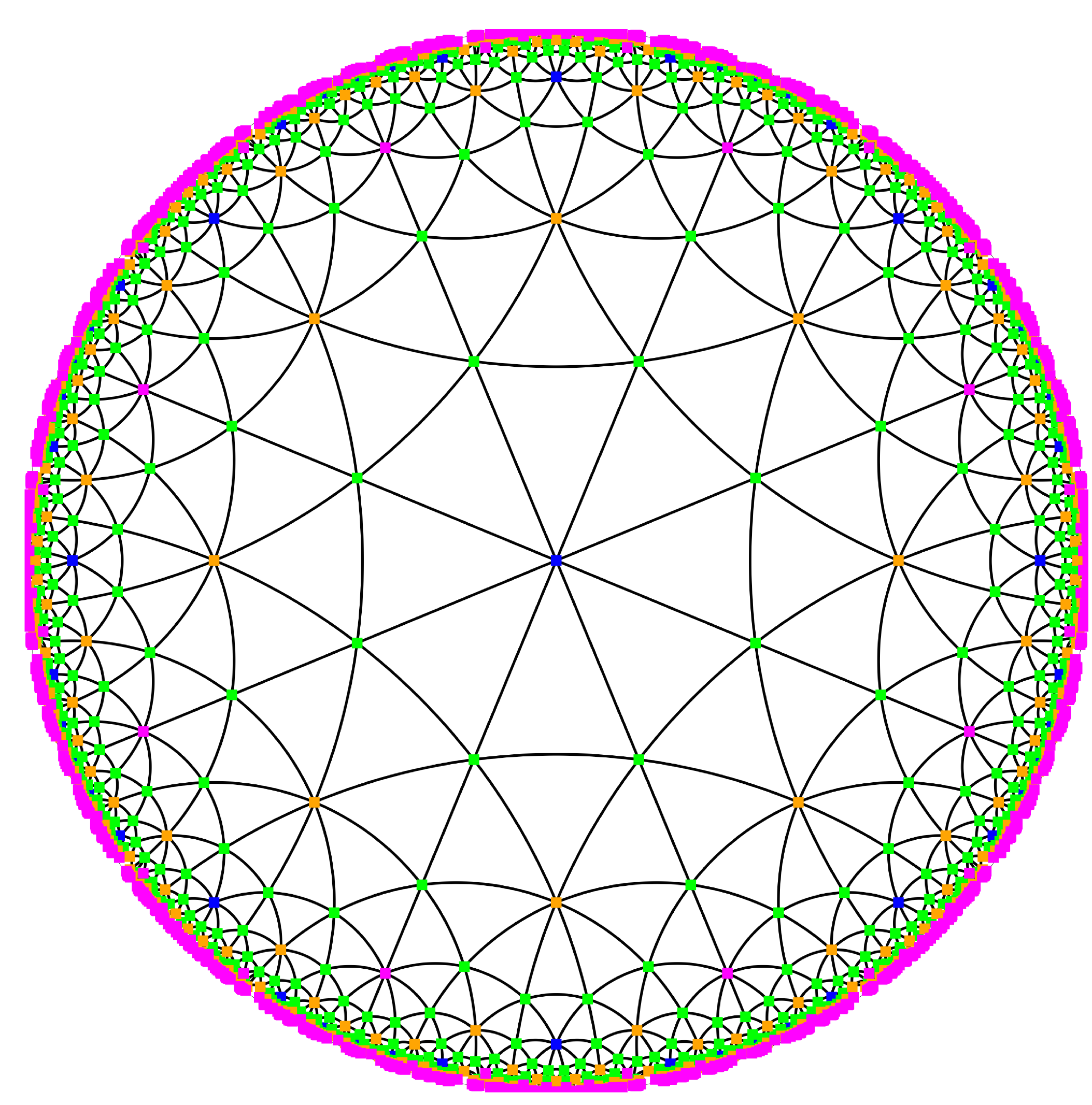
Moreover, while our solution for computing triangulations in hyperbolic spaces can be considered as ultimate [24], the case of hyperbolic manifolds has hardly been explored. Hyperbolic manifolds are quotients of a hyperbolic space by some group of hyperbolic isometries. Their triangulations can be seen as hyperbolic periodic triangulations. Periodic hyperbolic triangulations and meshes appear for instance in geometric modeling [55], neuromathematics [37], or physics [58]. Even the simplest possible case (a surface homeomorphic to the torus with two handles) shows strong mathematical difficulties [25], [60].