Section: Research Program
Slow-fast dynamics in neuronal models
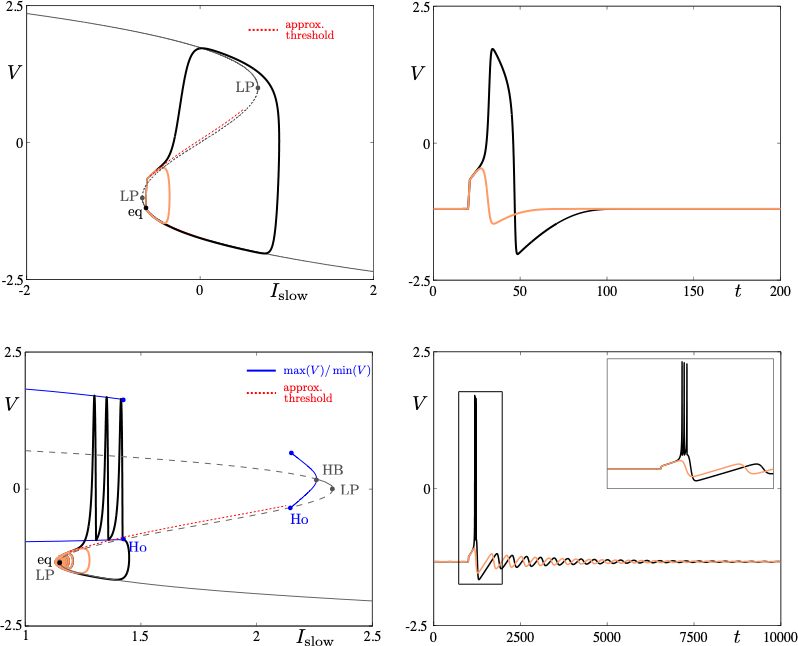
Neuronal rhythms typically display many different timescales, therefore it is important to incorporate this slow-fast aspect in models. We are interested in this modeling paradigm where slow-fast point models, using Ordinary Differential Equations (ODEs), are investigated in terms of their bifurcation structure and the patterns of oscillatory solutions that they can produce. To insight into the dynamics of such systems, we use a mix of theoretical techniques — such as geometric desingularisation and centre manifold reduction [44] — and numerical methods such as pseudo-arclength continuation [36]. We are interested in families of complex oscillations generated by both mathematical and biophysical models of neurons. In particular, so-called mixed-mode oscillations (MMOs) [5], [34], [43], which represent an alternation between subthreshold and spiking behaviour, and bursting oscillations [35], [41], also corresponding to experimentally observed behaviour [32]; see Figure 2. We are working on extending these results to spatially-extended neural models [2].