Section: New Results

Electromagnetic wave propagation

POD-based reduced-order DGTD method

Participants : Stéphane Lanteri, Kun Li [UESTC, Chengdu, China] , Liang Li [UESTC, Chengdu, China] .

This study is concerned with reduced-order modeling for time-domain electromagnetics and nanophotonics. More precisely, we consider the applicability of the proper orthogonal decomposition (POD) technique for the system of 3D time-domain Maxwell equations, possibly coupled to a Drude dispersion model, which is employed to describe the interaction of light with nanometer scale metallic structures. We introduce a discontinuous Galerkin (DG) approach for the discretization of the problem in space based on an unstructured tetrahedral mesh. A reduced subspace with a significantly smaller dimension is constructed by a set of POD basis vectors extracted offline from snapshots that are obtained by the global DGTD scheme with a second order leap-frog method for time integration at a number of time levels. POD-based ROM is established by projecting (Galerkin projection) the global semi-discrete DG scheme onto the low-dimensional space. The stability of the POD-based ROM equipped with the second order leap-frog time scheme has been analysed through an energy method. Numerical experiments have allowed to verify the accuracy, and demonstrate the capabilities of the POD-based ROM. These very promising preliminary results are currently consolidated by assessing the efficiency of the proposed POD-based ROM when applied to the simulation of 3D nanophotonic problems.

Numerical treatment of non-local dispersion for nanoplasmonics

Participants : Herbert de Gersem [TEMF, Technische Universität Darmstadt, Germany] , Stéphane Lanteri, Antoine Moreau [Université Clermont Auvergne] , Claire Scheid, Dimitrios Loukrezis [TEMF, Technische Universität Darmstadt, Germany] , Serge Nicaise [Université de Valenciennes et du Hainaut-Cambresis] , Armel Pitelet [Université Clermont Auvergne] , Nikolai Schmitt, Jonathan Viquerat.

When metallic nanostructures have sub-wavelength sizes and the illuminating frequencies are in the regime of metal's plasma frequency, electron interaction with the exciting fields have to be taken into account. Due to these interactions, plasmonic surface waves (called plasmons) can be excited and cause extreme local field enhancements. Exploiting such field enhancements in applications of interest requires a detailed knowledge about the occurring fields which can generally not be obtained analytically. For the numerical modeling of light-matter interaction on the nanoscale, the choice of an appropriate model is a crucial point. Approaches that are adopted in a first instance are based on local (no interaction between electrons) dispersion models e.g. Drude or Drude-Lorentz. From the mathematical point of view, these models lead to an additional ordinary differential equation in time that is coupled to Maxwell's equations. When it comes to very small structures in a regime of 2 nm to 25 nm, non-local response due to electron collisions have to be taken into account. This leads to additional, in general non-linear, partial differential equations and is significantly more difficult to treat, though. The classical model is based on a hydrodynamical approach that takes non-local response of the electrons into account. We in particular focus our attention on the linearized version of this model called Linearized Hydrodynamical Drude model. We conducted numerical studies in 2D (published in 2016) and 3D on a linearized hydrodynamic model (published in 2018). However differences between local and nonlocal response are still small. Especially for today’s fabrication precision, it remains a challenging task to find reliable structures where non-locality is dominant over e.g. geometrical errors. Motivated by trying to find experimental setups where non-locality is clearly distinguishable from other effects, we studied two promising structures, in close collaboration with physicists. First, in collaboration with A. Pitelet and A. Moreau from Université Clermont Auvergne, and D. Loukrezis and H. De Gersem from Technische Universität Darmstadt, we studied the impact of non-locality on gratings and showed that non-locality can affect surface plasmons propagating at the interface between a metal and a dielectric with a sufficiently high permittivity. We then design a grating coupler that should allow to experimentally observe this influence. Finally, we carefully set up a procedure to measure the signature of spatial dispersion precisely, paving the way for future experiments. Indeed, to ensure that the impact of non-locality exceeds geometric fabrication uncertainties, we proposed a post-fabrication characterization of the grating coupler. Based on the solution of inverse problems leading to the actually fabricated geometry and an uncertainty quantification (UQ) analysis, we conclude that non-locality should clearly be measurable in the grating coupler setting. This work has been submitted in a physics journal. Secondly in collaboration with A. Moreau we considered a nanocube setup that consists of an infinite gold ground layer plus a dielectric spacer of a given height above which a silver nanocube is chemically deposited. Due to this particular setting, the illumination of such a device is creating inside the gap between the nanocube and the ground layer (i.e. inside the dielectric layer) a gap plasmon that is very sensitive to non-locality. We proposed a surrogate-model based telemetry strategy in order to obtain the fabricated cube dimension (inverse problem). Based on this geometric characterization, we decreased the gap-size between the gold substrate and the silver cube and have compared local and non-local numerical simulations. We showed that the influence of non-locality exceeds the experimental error-bars for gap-sizes below 3.1  nm. Additionally, our nonlocal simulations are able to explain the discrepancy between the experiment and local simulations for very small gap-sizes. This project is still ongoing, since we are waiting for another set of experimental results.

On a theoretical side, we pursue the collaboration with S. Nicaise (Université de Valenciennes et du Hainaut-Cambresis) and proved well-posedness of the linearized non-local Drude model for various boundary conditions. We furthermore focused on establishing polynomial stability with optimal energy decay rate. We conducted a thorough study of energy stability for various numerical schemes and DG formulation using a general framework and finally numerically investigate the discrete polynomial stability. This work is almost finalized.

Study of 3D periodic structures at oblique incidences

Participants : Claire Scheid, Nikolai Schmitt, Jonathan Viquerat.

In this work, we focus on the development of the use of periodic boundary conditions with sources at oblique incidence in a DGTD framework. Whereas in the context of the Finite Difference Time Domain (FDTD) methods, an abundant literature can be found, for DGTD, the amount of contributions reporting on such methods is remarkably low. In this work, we supplement the existing references using the field transform technique with an analysis of the continuous system using the method of characteristics and provide an energy estimate. Furthermore, we also study the numerical stability of the resulting DGTD scheme. After numerical validations, two realistic test problems have been considered in the context of nanophotonics with our DIOGENeS DGTD solver. This work is under review.

Toward thermoplasmonics

Participants : Yves d'Angelo, Guillaume Baffou [Fresnel Institute, Marseille] , Stéphane Lanteri, Claire Scheid.

Although losses in metal is viewed as a serious drawback in many plasmonics experiments, thermoplasmonics is the field of physics that tries to take advantage of the latter. Indeed, the strong field enhancement obtained in nanometallic structures lead to a localized raise of the temperature in its vicinity leading to interesting photothermal effects. Therefore, metallic nanoparticles may be used as heat sources that can be easily integrated in various environments. This is especially appealing in the field of nanomedecine and can for example be used for diagnosis purposes or nanosurgery to cite but just a few. This year, we initiated a preliminary work towards this new field in collaboration with Y. D'Angelo (Université Côte d'Azur) and G. Baffou (Fresnel Institute, Marseille) who is an expert in this field. Due to the various scales and phenomena that come into play, the numerical modeling present great challenges. The laser illumination first excite a plasmon oscillation (reaction of the electrons of the metal) that relaxes in a thermal equilibrium and in turn excite the metal lattice (phonons). The latter is then responsible for heating the environment. A relevant modeling approach thus consists in describing the electron-phonon coupling through the evolution of their respective temperature. Maxwell's equations is then coupled to a set of coupled nonlinear hyperbolic equations describing the evolution of the temperatures of electrons, phonons and environment. The nonlinearities and the different time scales at which each thermalization occurs make the numerical approximation of these equations quite challenging.

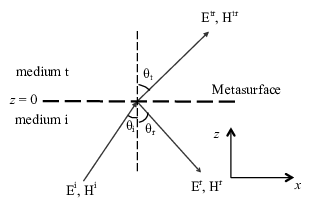
Numerical modeling of metasurfaces

Participants : Loula Fezoui, Patrice Genevet [CRHEA laboratory, Sophia Antipolis] , Stéphane Lanteri, Liang Li [UESTC, Chengdu, China] , Ronan Perrussel [Laplace laboratory, Toulouse] .

Metamaterials are composed of periodic subwavelength metal/dielectric structures that resonantly couple to the electric and/or magnetic components of the incident electromagnetic fields, exhibiting properties that are not found in nature. Planar metamaterials with subwavelength thickness, or metasurfaces, consisting of a layer of dielectric or plasmonic nanostructures, can be readily fabricated using lithography and nanoprinting methods, and the ultrathin thickness in the wave propagation direction can greatly suppress the undesirable losses. Metasurfaces enable a spatially varying optical response, mold optical wavefronts into shapes that can be designed at will, and facilitate the integration of functional materials to accomplish active control and greatly enhanced nonlinear response. Designing metasurfaces is generally a challenging inverse problem. A recently introduced synthesis techniques is based on so-called General Sheet Transition Conditions (GSTC) that can be leveraged to define the components of general bianisotropic surface susceptibility tensors characterizing the metasurface. A GSTC-based design technique has several advantages: 1) it is exact; 2) it is general, transforming arbitrary incident waves into arbitrary reflected and transmitted waves, 3) it often admits closed-form solutions, 4) it provides deep insight into the physics of the transformations, 5) it allows multiple (at least up to 4) simultaneous and independent transformations. We study the numerical treatment of GSTC in the time-domain and frequency-domain regimes in the DG and HDG settings respectively.

Corner effects in nanoplasmonics

Participants : Camille Carvalho [Applied Mathematics Department, University of California Merced, USA] , Patrick Ciarlet [ENSTA, POEMS project-team] , Claire Scheid.

In this work, we study nanoplasmonic structures with corners (typically a diedral/triangular structure). This is the central subject considered in the PhD thesis of Camille Carvalho. In the latter, the focus is made on a lossles Drude dispersion model with a frequency-domain approach. Several well posedness problems arise due to the presence of corners and are addressed in the PhD thesis. A time-domain approach in this context is also relevant and we propose to use the techniques developed in the team in this prospect. Even if both approaches (time-domain and frequency-domain) represent similar physical phenomena, problems that arise are different. These two approaches appear as complementary; it is thus worth bridging the gap between the two frameworks. We are currently performing a thorough comparison in the case of theses 2D structures with corners and we especially focus on the amplitude principle limit that raises a lot of questions.

MHM methods for the time-domain Maxwell equations

Participants : Alexis Gobé, Stéphane Lanteri, Diego Paredes Concha [Instituto de Matemáticas, Universidad Católica de Valparaiso, Chile] , Claire Scheid, Frédéric Valentin [LNCC, Petropolis, Brazil] .

Although the DGTD method has already been successfully applied to complex electromagnetic wave propagation problems, its accuracy may seriously deteriorate on coarse meshes when the solution presents multiscale or high contrast features. In other physical contexts, such an issue has led to the concept of multiscale basis functions as a way to overcome such a drawback and allow numerical methods to be accurate on coarse meshes. The present work, which is conducted in the context of the HOMAR Associate Team, is concerned with the study of a particular family of multiscale methods, named Multiscale Hybrid-Mixed (MHM) methods. Initially proposed for fluid flow problems, MHM methods are a consequence of a hybridization procedure which caracterize the unknowns as a direct sum of a coarse (global) solution and the solutions to (local) problems with Neumann boundary conditions driven by the purposely introduced hybrid (dual) variable. As a result, the MHM method becomes a strategy that naturally incorporates multiple scales while providing solutions with high order accuracy for the primal and dual variables. The completely independent local problems are embedded in the upscaling procedure, and computational approximations may be naturally obtained in a parallel computing environment. In this study, a family of MHM methods is proposed for the solution of the time-domain Maxwell equations where the local problems are discretized either with a continuous FE method or a DG method (that can be viewed as a multiscale DGTD method). Preliminary results have been obtained in the two-dimensional case.

MHM methods for the frequency-domain Maxwell equations

Participants : Théophile Chaumont-Frelet, Zakaria Kassali, Stéphane Lanteri, Frédéric Valentin [LNCC, Petropolis, Brazil] .

We have initiated this year a study of MHM methods for the system of frequency-domain Maxwell equations based on very promising results recently obtained by T. Chaumont-Frelet and F. Valentin for the Helmholtz equation. The design principles are very similar to those underlying MHM methods for the system of time-domain Maxwell equations however we expect to achieve more convincing results for highly multiscale problems since we do not have to deal with the time dimension in the present case. Part of this study is conducted in the context of the PHOTOM (PHOTOvoltaic solar devices in Multiscale computational simulations) Math-Amsud project.

HDG methods for the time-domain Maxwell equations

Participants : Stéphane Descombes, Stéphane Lanteri, Georges Nehmetallah.

This study is concerned with the development of accurate and efficient solution strategies for the system of 3D time-domain Maxwell equations coupled to local dispersion models (e.g. Debye, Drude or Drude-Lorentz models) in the presence of locally refined meshes. Such meshes impose a constraint on the allowable time step for explicit time integration schemes that can be very restrictive for the simulation of 3D problems. We consider here the possibility of using an unconditionally stable implicit time or a locally implicit time integration scheme combined to a HDG discretization method. As a preliminary step, we have investigated a fully explicit HDG method generalizing the classical upwind flux-based DG method for the system of time-domain Maxwell equations. We have studied the stability of this new HDG method and in particular, the influence of the stabilization parameter on the CFL condition. We are now progressing toward the design of a new family of high order in time hybrid explicit-implicit HDG methods to deal efficiently with CFL restriction due to grid-induced stiffness.

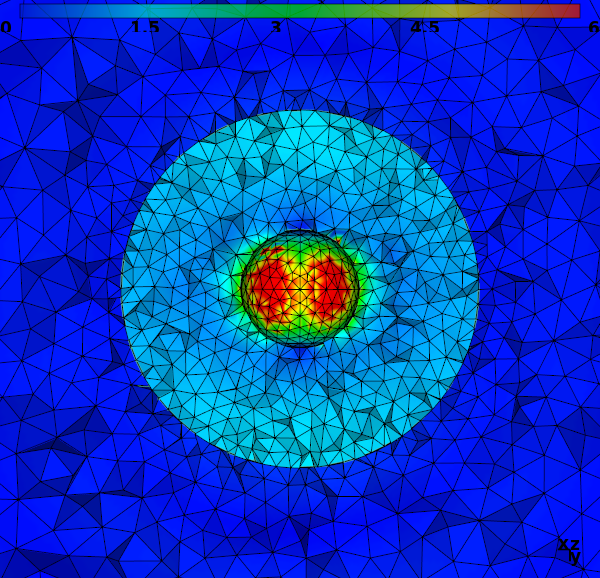
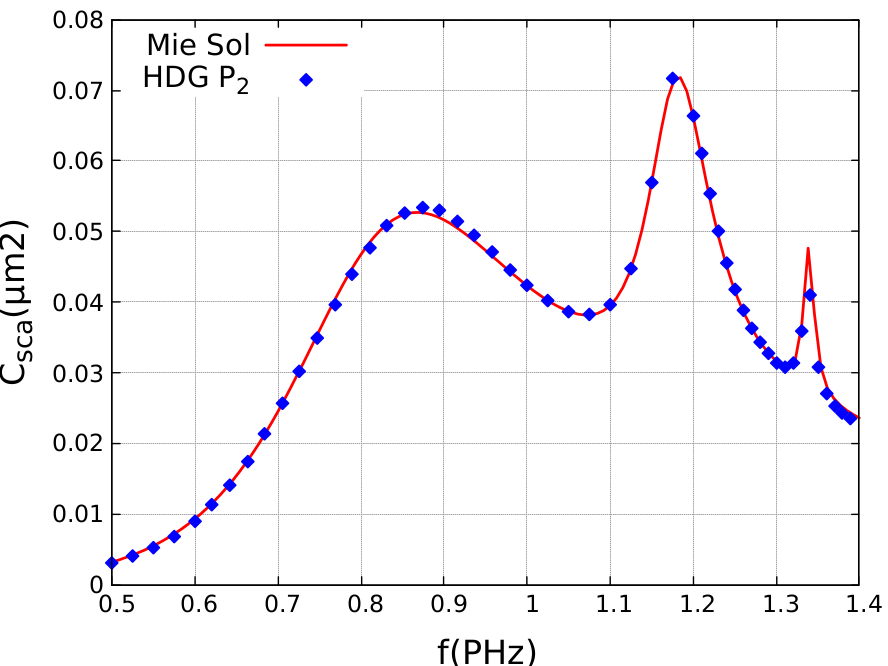
HDG methods for frequency-domain plasmonics

Participants : Stéphane Lanteri, Mostafa Javadzadeh Moghtader, Liang Li [UESTC, Chengdu, China] .

HDG method is a new class of DG family with significantly less globally coupled unknowns, and can leverage a post-processing step to gain super-convergence. Its features make HDG a possible candidate for computational electromagnetics applications, especially in the frequency-domain. The HDG method introduces an hybrid variable, which represents an additional unknown on each face of the mesh, and leads to a sparse linear system in terms of the degrees of freedom of the hybrid variable only. Our HDG method had been first introduced for the system of 3D time-harmonic Maxwell’s, combined to an iterative Schwarz domain decomposition (DD) algorithm to allow for an efficient parallel hybrid iterative-direct solver. The resulting DD-HDG solver has been applied to classical applications of electromagnetics in the microwave regime. In the present study we further focus on this particular physical context and propose a arbitrary high order HDG method for solving the system of 3D frequency-domain Maxwell equations coupled to a generalized model of physical dispersion in metallic nanostructures at optical frequencies. Such a generalized dispersion model unifies most common dispersion models, like Drude and Drude-Lorentz models, and it permits to fit large range of experimental data. The resulting DD-HDG solver is capable of using different element types and orders of approximation, hence enabling the possibilities of $p$-adaptivity and non-conforming meshing, and proves to have interesting potentials for modeling of complex nanophotonic and nanoplasmonic problems.