Section: Application Domains
Applications Domains
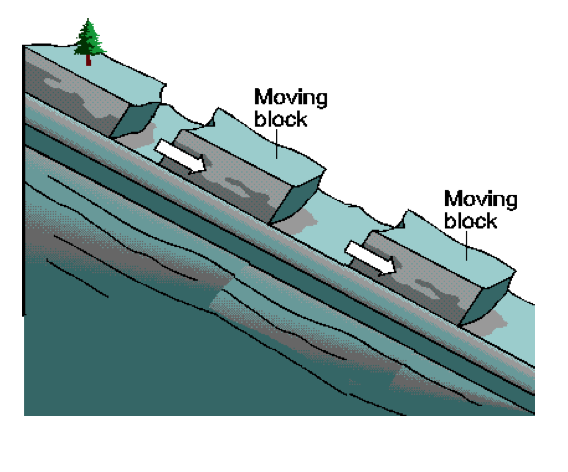
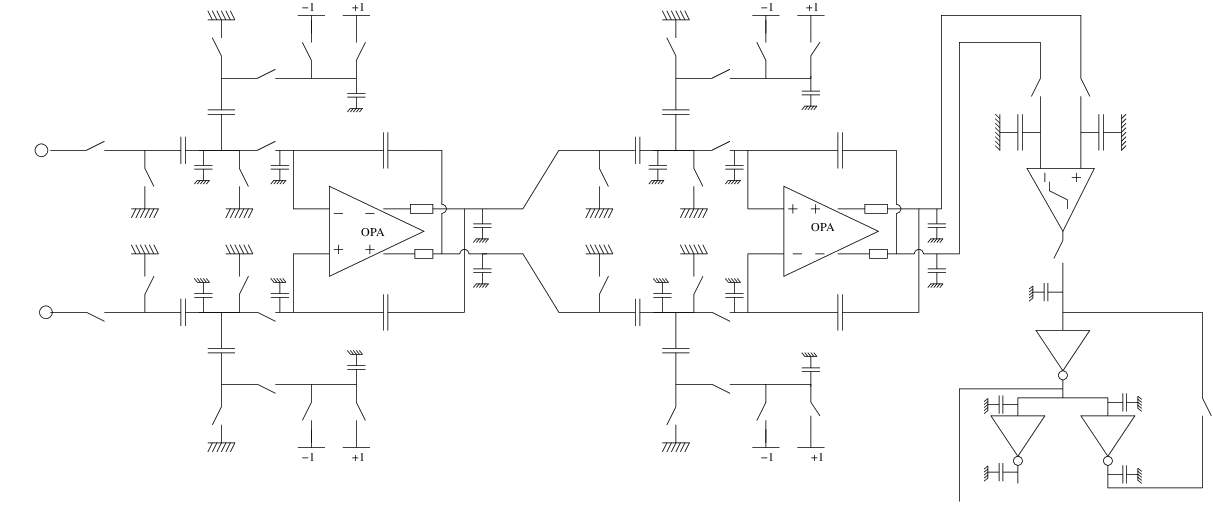
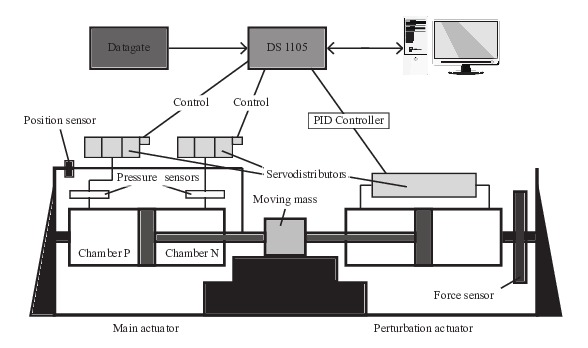
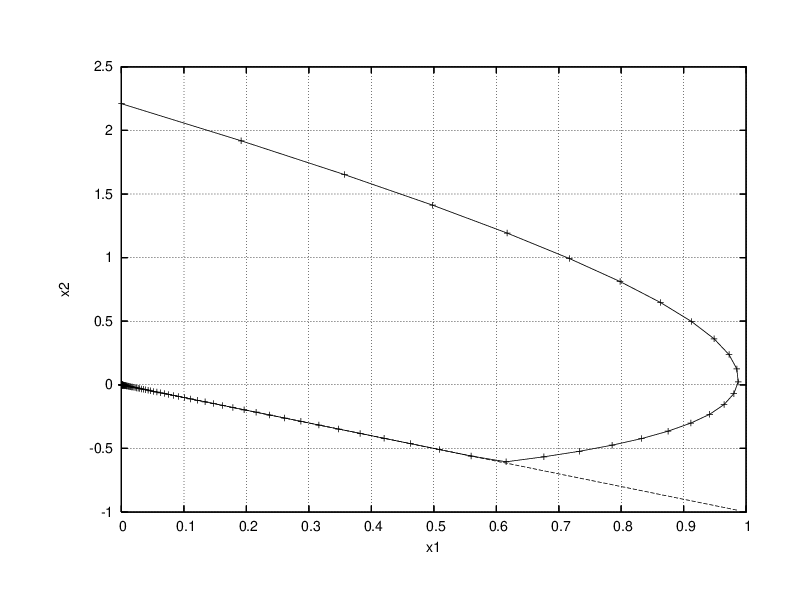
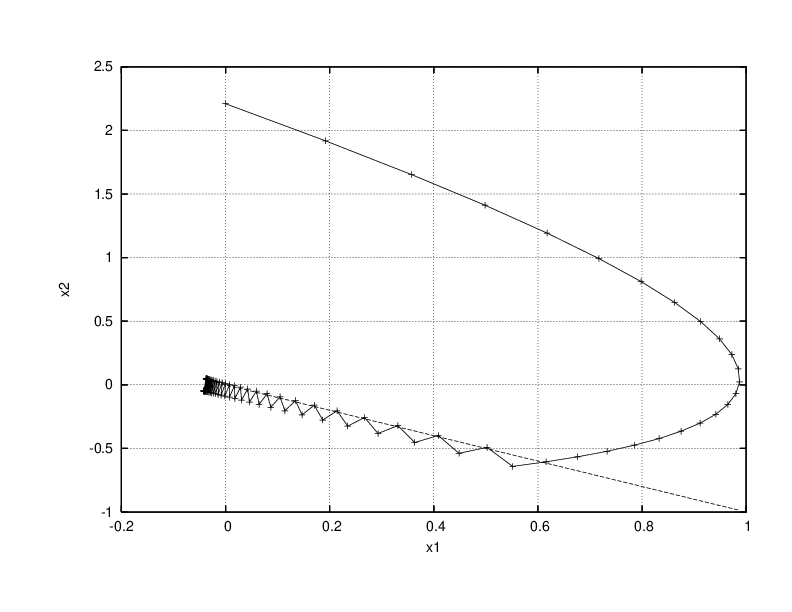
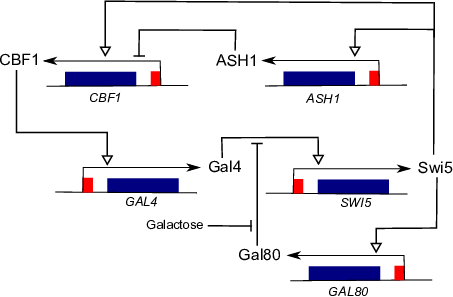
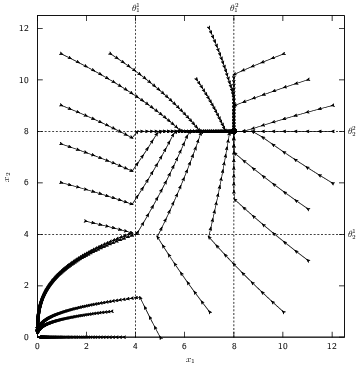
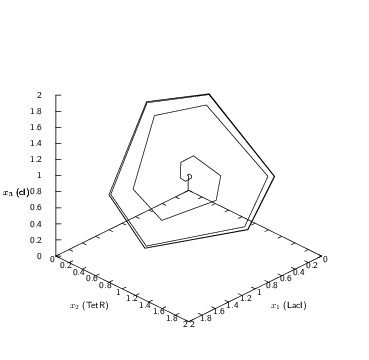
Nonsmooth dynamical systems arise in a lot of application fields. We briefly expose here some applications that have been treated in the BIPOP team and that we will continue in the TRIPOP team, as a validation for the research axes and also in terms of transfer (Sect. 7.1). In mechanics, the main instances of nonsmooth dynamical systems are multibody systems with Signorini's unilateral contact, set-valued (Coulomb-like) friction and impacts, or in continuum mechanics, ideal plasticity, fracture or damage. Some illustrations are given in Figure 4(a-f). Other instances of nonsmooth dynamical systems can also be found in electrical circuits with ideal components (see Figure 4(g)) and in control theory, mainly with sliding mode control and variable structure systems (see Figure 4(h)). More generally, every time a piecewise, possibly set–valued, model of systems is invoked, we end up with a nonsmooth system. This is the case, for instance, for hybrid systems in nonlinear control or for piecewise linear modeling of gene regulatory networks in mathematical biology (see Figure 4(i)). Another common example of nonsmooth dynamics is also found when the vector field of a dynamical system is defined as a solution of an optimization problem under constraints, or a variational inequality. Examples of this kind are found in the optimal control theory, in dynamic Nash equilibrium or in the theory of dynamic flows over networks.