Section: New Results
Modeling for Oceanic and Atmospheric flows
Numerical Schemes for Ocean Modelling
Participants : Eric Blayo, Matthieu Brachet, Laurent Debreu, Emilie Duval, Christopher Eldred, Nicholas Kevlahan, Florian Lemarié, Gurvan Madec, Farshid Nazari.
The increase of model resolution naturally leads to the representation of a wider energy spectrum. As a result, in recent years, the understanding of oceanic submesoscale dynamics has significantly improved. However, dissipation in submesoscale models remains dominated by numerical constraints rather than physical ones. Effective resolution is limited by the numerical dissipation range, which is a function of the model numerical filters (assuming that dispersive numerical modes are efficiently removed). As an example, the stabilization of the coupling between barotropic (fast) and baroclinic (slow) modes in a three dimensional ocean model is a source of large numerical dissipation. This has been studied in details in [6].
F. Lemarié and L. Debreu (with H. Burchard, K. Klingbeil and J. Sainte-Marie) have organized the international COMMODORE workshop on numerical methods for oceanic models (Paris, Sept. 17-19, 2018). https://commodore2018.sciencesconf.org/, see [12] for a summary of the scientific discussions. The next COMMODORE meeting is planned for February 2020 and will take place in Hamburg. https://www.conferences.uni-hamburg.de/event/76.
With the increase of resolution, the hydrostatic assumption becomes less valid and the AIRSEA group also works on the development of non-hydrostatic ocean models. The treatment of non-hydrostatic incompressible flows leads to a 3D elliptic system for pressure that can be ill conditioned in particular with non geopotential vertical coordinates. That is why we favour the use of the non-hydrostatic compressible equations that removes the need for a 3D resolution at the price of reincluding acoustic waves [29].
In addition, Emilie Duval started her PhD in September 2018 on the coupling between the hydrostatic incompressible and non-hydrostatic compressible equations.
The team is involved in the HEAT (Highly Efficient ATmospheric Modelling) ANR project. This project aims at developing a new atmospheric dynamical core (DYNAMICO) discretized on an icosahedral grid. This project is in collaboration with Ecole Polytechnique, Meteo-France, LMD, LSCE and CERFACS. In the context of the HEAT project, we worked on the analysis of dispersion analysis of continuous and discontinuous Galerkin methods of arbitrary degree of approximation ([31]), on compatible Galerkin schemes for shallow water model in 2D ([9]). In addition, we worked on the discrete formulation of the thermal rotating shallow water equations. This formulation, based on quasi-Hamiltonian discretizations methods, allows for the first time total mass, buoyancy and energy conservation to machine precision ([8]).
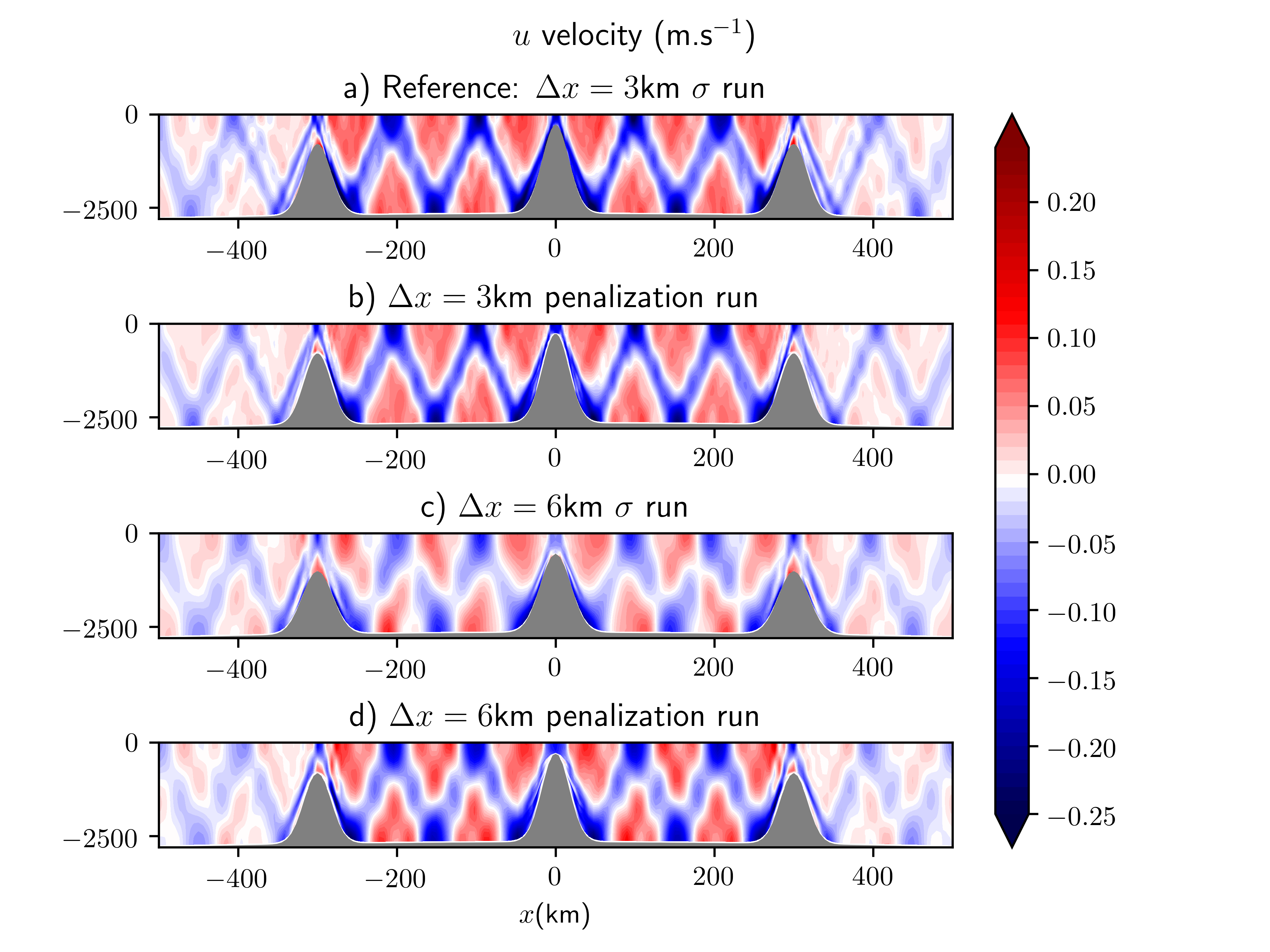
Accurate and stable implementation of bathymetry boundary conditions in ocean models remains a challenging problem. The dynamics of ocean flow often depend sensitively on satisfying bathymetry boundary conditions and correctly representing their complex geometry. Generalized (e.g. ) terrain-following coordinates are often used in ocean models, but they require smoothing the bathymetry to reduce pressure gradient errors. Geopotential -coordinates are a common alternative that avoid pressure gradient and numerical diapycnal diffusion errors, but they generate spurious flow due to their “staircase” geometry. In [5], we introduce a new Brinkman volume penalization to approximate the no-slip boundary condition and complex geometry of bathymetry in ocean models. This approach corrects the staircase effect of -coordinates, does not introduce any new stability constraints on the geometry of the bathymetry and is easy to implement in an existing ocean model. The porosity parameter allows modelling subgrid scale details of the geometry. We illustrate the penalization and confirm its accuracy by applying it to three standard test flows: upwelling over a sloping bottom, resting state over a seamount and internal tides over highly peaked bathymetry features.
Figure (1) shows strong improvements obtained when the penalization method is used in comparison with traditional terrain following simulations. At 6km resolution, the penalization methods (Figure (1) d)), that takes into account details of bathymetry, allows to recover internal tide wave beams closed to the 3km simulation. (Figure (1) a)).
|
Coupling Methods for Oceanic and Atmospheric Models
Participants : Eric Blayo, Florian Lemarié, Sophie Thery, Simon Clément.
Coupling methods routinely used in regional and global climate models do not provide the exact solution to the ocean-atmosphere problem, but an approximation of one [49]. For the last few years we have been actively working on the analysis of ocean-atmosphere coupling both in terms of its continuous and numerical formulation (see [21] for an overview). Our activities can be divided into four general topics
-
Stability and consistency analysis of existing coupling methods: in [49] we showed that the usual methods used in the context of ocean-atmosphere coupling are prone to splitting errors because they correspond to only one iteration of an iterative process without reaching convergence. Moreover, those methods have an additional condition for the coupling to be stable even if unconditionally stable time-stepping algorithms are used. This last remark was further studied in [37] and it turned out to be a major source of instability in atmosphere-snow coupling.
-
Study of physics-dynamics coupling: during the PhD-thesis of Charles Pelletier the scope was on including the formulation of physical parameterizations in the theoretical analysis of the coupling, in particular the parameterization schemes to compute air-sea fluxes [56]. To do so, a metamodel representative of the behavior of the full parameterization but with a continuous form easier to manipulate has been derived thanks to a sensitivity analysis. This metamodel is more adequate to conduct the mathematical analysis of the coupling while being physically satisfactory [57]. More recently we have started to work specifically on the discretization methods for the parameterization of planetary boundary layers in climate models [51] which takes the form of an nonstationary nonlinear parabolic equation. The objective is to derive a discretization for which we could prove nonlinear stability criteria and show robustness to large variations in parabolic Courant number while being consistent with our knowledge of the underlying physical principles (e.g. the Monin-Obukhov theory in the surface layer).This work will continue in the framework of the PhD-thesis of C. Simon.
-
A simplified atmospheric boundary layer model for oceanic purposes: Part of our activities within the IMMERSE project is dedicated to the development of a simplified model of the marine atmospheric boundary layer of intermediate complexity between a bulk parameterization and a full three-dimensional atmospheric model and to its integration to the NEMO general circulation model [24]. A constraint in the conception of such a simplified model is to allow an apt representation of the downward momentum mixing mechanism and partial re-energization of the ocean by the atmosphere while keeping the computational efficiency and flexibility inherent to ocean only modeling. A paper is in preparation and will be submitted in early 2020.
-
Analysis of air-sea-wave interactions in realistic high-resolution realistic simulations: part of our activity has been in collaboration with atmosphericists and physical oceanographers to study the impact on some modeling assumptions (e.g. [50]) in large-scale realistic ocean-atmosphere coupled simulations [16], [53]. Moreover, within the ALBATROS project [23], we have contributed to the development of a 2-way coupling between an ocean global circulation model (NEMO) with a surface wave model (WW3). Such coupling is not straightforward to implement since it requires modifications of the governing equations, boundary conditions and subgrid scale closures in the oceanic model. A paper is currently under open discussion in Geoscientific Model Development journal on that topic [4].
-
Efficient coupling methods: we have been developing coupling approaches for several years, based on so-called Schwarz algorithms. In particular, we addressed the development of efficient interface conditions for multi-physics problems representative of air-sea coupling [61] (paper in preparation). This work is done in the framework of S. Théry PhD (started in fall 2017). During the internship of C. Simon, efficient interface conditions have been derived at a (semi)-discrete level and can thus be systematically compared with the ones obtained from the continuous problem.
These topics are addressed through strong collaborations between the applied mathematicians and the climate community (Meteo-France, Ifremer, LMD, and LOCEAN). Our work on ocean-atmosphere coupling has steadily matured over the last few years and has reached a point where it triggered interest from the climate community. Through the funding of the COCOA ANR project (started in January 2017, PI: E. Blayo), Airsea team members play a major role in the structuration of a multi-disciplinary scientific community working on ocean-atmosphere coupling spanning a broad range from mathematical theory to practical implementations in climate models. An expected outcome of this project should be the design of a benchmark suite of idealized coupled test cases representative of known issues in coupled models. Such idealized test cases should motivate further collaborations at an international level. In this context, a single-column version of the CNRM climate models has been designed and several coupling algorithms have been implemented (work done by S. Valcke, CERFACS). This model will be used to illustrate the relevance of our theoretical work in a semi-realistic context.
Data assimilation for coupled models
In the context of operational meteorology and oceanography, forecast skills heavily rely on proper combination of model prediction and available observations via data assimilation techniques. Historically, numerical weather prediction is made separately for the ocean and the atmosphere in an uncoupled way. However, in recent years, fully coupled ocean-atmosphere models are increasingly used in operational centers to improve the reliability of seasonal forecasts and tropical cyclones predictions. For coupled problems, the use of separated data assimilation schemes in each medium is not satisfactory since the result of such assimilation process is generally inconsistent across the interface, thus leading to unacceptable artefacts. Hence, there is a strong need for adapting existing data assimilation techniques to the coupled framework. As part of our ERACLIM2 contribution three general data assimilation algorithms, based on variational data assimilation techniques, have been developed and applied to a single column coupled model. The dynamical equations of the considered problem are coupled using an iterative Schwarz domain decomposition method. The aim is to properly take into account the coupling in the assimilation process in order to obtain a coupled solution close to the observations while satisfying the physical conditions across the air-sea interface. Results shows significant improvement compared to the usual approach on this simple system. The aforementioned system has been coded within the OOPS framework (Object Oriented Prediction System) in order to ease the transfer to more complex/realistic models.
Following this line of research, CASIS, a collaborative project with Mercator Océan started late 2017 until end of 2019 in order to extend these developments to iterative Kalman smoother data assimilation scheme, in the framework of a coupled ocean-atmospheric boundary layer context.
Optimal control of grids and schemes for ocean model.
Participants : Laurent Debreu, Eugene Kazantsev.
In [28], variational data assimilation technique is applied to a simple bidimensional wave equation that simulates propagation of internal gravity waves in the ocean in order to control grids and numerical schemes. Grid steps of the vertical grid, Brunt-Vaisala frequency and approximation of the horizontal derivative were used as control parameters either separately or in the joint control. Obtained results show that optimized parameters may partially compensate errors committed by numerical scheme due to insufficient grid resolution.
Optimal vertical grid steps and coefficients in horizontal derivative approximation found in the variational control procedure allow us to get the model solution that is rather close to the solution of the reference model. The error in the wave velocity on the coarse grid is mostly compensated in experiments with joint control of parameters while the error in the wave amplitude occurs to be more difficult to correct.
However, optimal grid steps and discretization schemes may be in a disagreement with requirements of other model physics and additional analysis of obtained optimized parameters from the point of view of they agreement with the model is necessary.
Machine learning for parametrisation of the model dissipation.
Participants : Laurent Debreu, Eugene Kazantsev, Arthur Vidard, Olivier Zahm.
Artificial intelligence and machine learning may be considered as a potential way to address unresolved model scales and to approximate poorly known processes such as dissipation that occurs essentially at small scales. In order to understand the possibility to combine numerical model and neural network learned with the aid of external data, we develop a network generation and learning algorithm and use it to approximate nonlinear model operators. Beginning with a simple nonlinear equations like transport-diffusion and Burgers ones, we use artificially generated external data to learn the network by Adam algorithm [47]. Results show the possibility to approximate nonlinear, and even discontinuous dissipation operator with a quite good accuracy, however, several millions iterations are necessary to learn.
Nonhydrostatic Modeling
Participants : Eric Blayo, Laurent Debreu, Emilie Duval.
In the context of the French initiative CROCO (Coastal and Regional Ocean COmmunity model, https://www.croco-ocean.org) for the development of a new oceanic modeling system, Emilie Duval is working on the design of methods to couple local nonhydrostatic models to larger scale hydrostatic ones (PhD started in Oct. 2018). Such a coupling is quite delicate from a mathematical point of view, due to the different nature of hydrostatic and nonhydrostatic equations (where the vertical velocity is either a diagnostic or a prognostic variable). A prototype has been implemented, which allows for analytical solutions in simplified configurations and will make it possible to test different numerical approaches.