Section: Overall Objectives

Scientific grounds

Mesh generation is a notoriously difficult task. A quick search on the NSF grant web page (https://www.nsf.gov/awardsearch) with “mesh generation AND finite element” keywords returns more than 30 currently active grants for a total of $8 million. NASA indicates mesh generation as one of the major challenges for 2030  [36], and estimates that it costs 80% of time and effort in numerical simulation. This is due to the need for constructing supports that match both the geometry and the physics of the system to be modeled. In our team we pay a particular attention to scientific computing, because we believe it has a world changing impact.

It is very unsatisfactory that meshing, i.e. just “preparing the data” for the simulation, eats up the major part of the time and effort. Our goal is to make the situation evolve, by studying the influence of shapes and discretizations, and inventing new algorithms to automatically generate meshes that can be directly used in scientific computing. This goal is a result of our progressive shift from pure graphics (“Geometry and Lighting”) to real world problems (“Shape Fidelity”).

Figure 1. There is a wide range of possibilities to discretize a given domain. (A) Completely unstructured, white noise point sampling; (B) Blue noise point sampling exhibits some structure; (C) tetrahedral mesh; (D) hexahedral mesh.

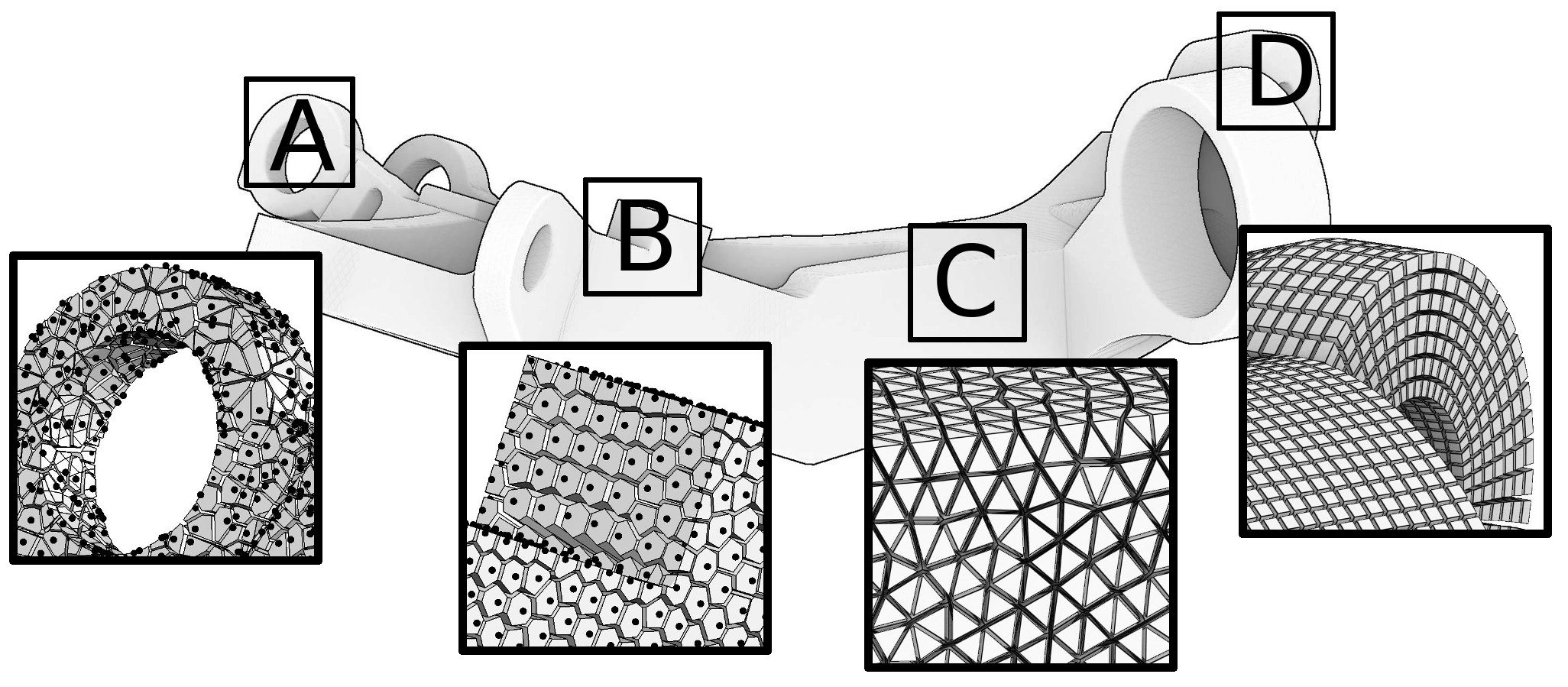
Meshing is so central in geometric modeling because it provides a way to represent functions on the objects studied (texture coordinates, temperature, pressure, speed, etc.). There are numerous ways to represent functions, but if we suppose that the functions are piecewise smooth, the most versatile way is to discretize the domain of interest. Ways to discretize a domain range from point clouds to hexahedral meshes; let us list a few of them sorted by the amount of structure each representation has to offer (refer to Figure 1).

• At one end of the spectrum there are point clouds: they exhibit no structure at all (white noise point samples) or very little (blue noise point samples). Recent explosive development of acquisition techniques (e.g. scanning or photogrammetry) provides an easy way to build 3D models of real-world objects that range from figurines and cultural heritage objects to geological outcrops and entire city scans. These technologies produce massive, unstructured data (billions of 3D points per scene) that can be directly used for visualization purposes, but this data is not suitable for high-level geometry processing algorithms and numerical simulations that usually expect meshes. Therefore, at the very beginning of the acquisition-modeling-simulation-analysis pipeline, powerful scan-to-mesh algorithms are required.

  During the last decade, many solutions have already been proposed  [16], [12], [14], [15], [13], but the problem of building a good mesh from scattered 3D points is far from being solved. Beside the fact that the data is unusually large, the existing algorithms are challenged also by the extreme variation of data quality. Raw point clouds have many defects, they are often corrupted with noise, redundant, incomplete (due to occlusions): they all are uncertain.

• Triangulated surfaces are ubiquitous, they are the most widely used representation for 3D objects. Some applications like 3D printing do not impose heavy requirements on the surface: typically it has to be watertight, but triangles can have an arbitrary shape. Other applications like texturing require very regular meshes, because they suffer from elongated triangles with large angles.

  While being a common solution for many problems, triangle mesh generation is still an active topic of research. The diversity of representations (meshes, NURBS, ...) and file formats often results in a “Babel” problem when one has to exchange data. The only common representation is often the mesh used for visualization, that has in most cases many defects, such as overlaps, gaps or skinny triangles. Re-injecting this solution into the modeling-analysis loop is non-trivial, since again this representation is not well adapted to analysis.

• Tetrahedral meshes are the volumic equivalent of triangle meshes, they are very common in the scientific computing community. Tetrahedral meshing is now a mature technology. It is remarkable that still today all the existing software used in the industry is built on top of a handful of kernels, all written by a small number of individuals [23], [34], [40], [25], [33], [35], [24], [11]. Meshing requires a long-term, focused, dedicated research effort, that combines deep theoretical studies with advanced software development. We have the ambition bring to this kind of maturity a different type of mesh (structured, with hexahedra), which is highly desirable for some simulations, and for which, unlike tetrahedra, no satisfying automatic solution exists. In the light of recent contributions, we believe that the domain is ready to overcome the principal difficulties.

• Finally, at the most structured end of the spectrum there are hexahedral meshes composed of deformed cubes (hexahedra). They are preferred for certain physics simulations (deformation mechanics, fluid dynamics ...) because they can significantly improve both speed and accuracy. This is because (1) they contain a smaller number of elements (5-6 tetrahedra for a single hexahedron), (2) the associated tri-linear function basis has cubic terms that can better capture higher order variations, (3) they avoid the locking phenomena encountered with tetrahedra [18], (4) hexahedral meshes exploit inherent tensor product structure and (5) hexahedral meshes are superior in direction dominated physical simulations (boundary layer, shock waves, etc). Being extremely regular, hexahedral meshes are often claimed to be The Holy Grail for many finite element methods  [19], outperforming tetrahedral meshes both in terms of computational speed and accuracy.

  Despite 30 years of research efforts and important advances, mainly by the Lawrence Livermore National Labs in the U.S. [39], [38], hexahedral meshing still requires considerable manual intervention in most cases (days, weeks and even months for the most complicated domains). Some automatic methods exist [28], [42], that constrain the boundary into a regular grid, but they are not fully satisfactory either, since the grid is not aligned with the boundary. The advancing front method [17] does not have this problem, but generates irregular elements on the medial axis, where the fronts collide. Thus, there is no fully automatic algorithm that results in satisfactory boundary alignment.