Section: Overall Objectives

Overall Objectives

Our research addresses the broad application domain of cryptography and cryptanalysis from the algorithmic perspective. We study all the algorithmic aspects, from the top-level mathematical background down to the optimized high-performance software implementations. Several kinds of mathematical objects are commonly encountered in our research. Some basic ones are truly ubiquitous: integers, finite fields, polynomials, real and complex numbers. We also work with more structured objects such as number fields, algebraic curves, or polynomial systems. In all cases, our work is geared towards making computations with these objects effective and fast.

The two facets of cryptology—cryptography and cryptanalysis—are central to our research. The key challenges are the assessment of the security of proposed cryptographic primitives (both public- and secret-key), as well as the introduction of new cryptographic primitives, or the performance improvement of existing ones.

Our research connects to both symmetric and asymmetric key cryptography. While the basic principles of these domains are rather different—indeed their names indicate different handlings of the key—research in both domains is led by the same objective of finding the best trade-offs between efficiency and security. In addition to this, both require to study design and analysis together as these two aspects nurture each other.

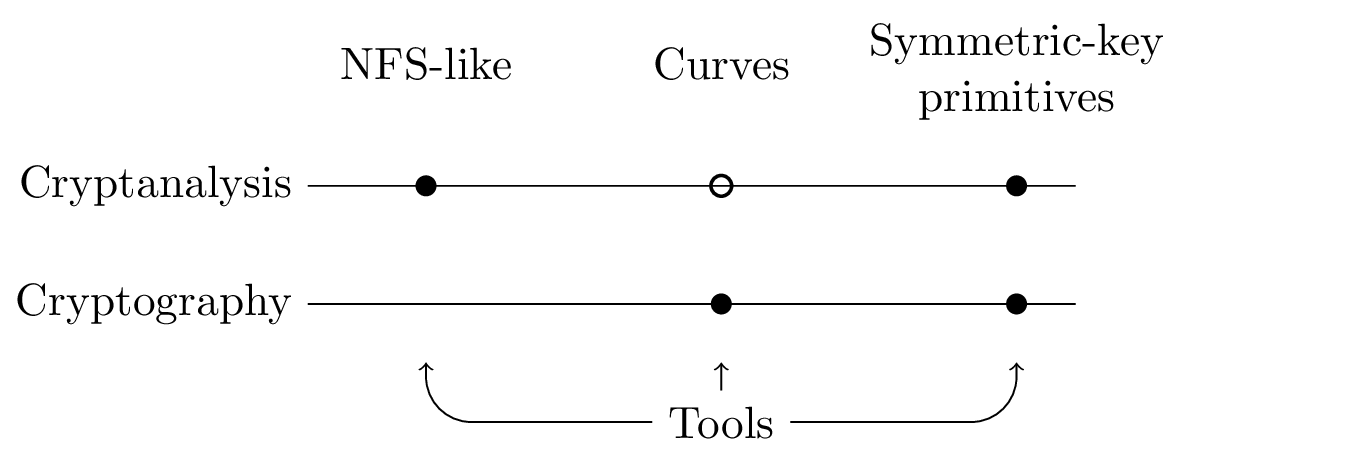
Our research topics can be listed either with broad applications domains in mind (a very coarse-grain view would have us list them under cryptography and cryptanalysis), or more thematically (see Figure 1). Either way, we also identify a set of tools that we sometimes develop per se, but most often as ingredients towards goals that are set in the context of other themes. Following the “vertical” reading direction in Figure 1, our research topics are as follows.

• Extended NFS family. A common algorithmic framework, called the Number Field Sieve (NFS), addresses both the integer factorization problem as well as the discrete logarithm problem over finite fields. We have numerous algorithmic contributions in this context, and develop software to illustrate them.

  We plan to improve on the existing state of the art in this domain by researching new algorithms, by optimizing the software performance, and by demonstrating the reach of our software with highly visible computations.

• Algebraic curves and their Jacobians. We develop algorithms and software for computing essential properties of algebraic curves for cryptology, eventually enabling their widespread cryptographic use.

  One of the challenges we address here is point counting. In a wider perspective, we also study the link between abelian varieties over finite fields and principally polarized abelian varieties over fields of characteristic zero, together with their endomorphism ring. In particular, we work in the direction of making this link an effective one. We are also investigating various approaches for attacking the discrete logarithm problem in Jacobians of algebraic curves. Questions more recently studied include the development of cryptosystems based on isogenies.

• Symmetric key cryptography. This topic has emerged recently in the team, with the recruiting of Marine Minier and Virginie Lallemand. We are interested in particular in automatic tools for new paradigms of cryptanalysis, going beyond the classical linear and differential cryptanalysis techniques. Newer, more intricate techniques are rather hard to apply and are error-prone. The idea is then to automate the analysis process by developing tools implemented in CP, SAT or MILP. We plan to pay special attention to the recent advances in cryptanalysis and to study recently proposed lightweight ciphers.

  In addition, we also study new designs. The challenge of the lightweight world pushes symmetric cryptography to be ever more efficient while guaranteeing the same level of security as before. It is thus very important to scrutinize each building block of the symmetric key primitives to be convinced of their security.

• Tools. Several mathematical objects are pervasive in our research. We sometimes study them per se, but they most often play a key role in the work related to the topics above. In particular, we study computer arithmetic, polynomial systems, linear algebra. In the context of symmetric cryptography, the mathematical objects we deal with are rather different: we are mainly interested in small (4 or 8 bits) non-linear permutations (the so-called S-boxes) and in linear transformations based on coding theory (Maximum Distance Separable (MDS) matrices or quasi-MDS matrices).

  Our goals with all these basic objects include a strong commitment to providing high-quality software that can be used as a dependable building block in our research.

As a complement to the last point, we consider that the impact of our research on cryptology in general owes a lot to the publication of concrete practical results. We are strongly committed to making our algorithms available as software implementations. We thus have several long-term software development projects that are, and will remain, part of our research activity.