Section: Research Program

Enhance the computational and logical power of proof assistants

The democratisation of proof assistants based on type theory has likely been impeded one central problem: the mismatch between the conception of equality in mathematics and its formalisation in type theory. Indeed, some basic principles that are used implicitly in mathematics—such as Church’s principle of propositional extensionality, which says that two propositions are equal when they are logically equivalent—are not derivable in type theory. Even more problematically, from a computer science point of view, the basic concept of two functions being equal when they are equal at every “point” of their domain is also not derivable: rather, it must be added as an additional axiom. Of course, these principles are consistent with type theory so that working under the corresponding additional assumptions is safe. But the use of these assumptions in a definition potentially clutters its computational behaviour: since axioms are computational black boxes, computation gets stuck at the points of the code where they have been used.

We propose to investigate how expressive logical transformations such as forcing [70] and sheaf construction might be used to enhance the computational and logical power of proof assistants—with a particular emphasis on their implementation in the Coq proof assistant by the means of effective translations (or compilation phases). One of the main topics of this task, in connection to the ERC project CoqHoTT, is the integration in Coq of new concepts inspired by homotopy type theory [107] such as the univalence principle, and higher inductive types.

A definitional proof-irrelevant version of Coq.

In the Coq proof assistant, the sort $\mathrm{𝐏𝐫𝐨𝐩}$ stands for the universe of types which are propositions. That is, when a term $P$ has type $\mathrm{𝐏𝐫𝐨𝐩}$, the only relevant fact is whether $P$ is inhabited (that is true) or not (that is false). This property, known as proof irrelevance, can be expressed formally as: $\forall xy:P,x=y$. Originally, the raison d'être of the sort $\mathrm{𝐏𝐫𝐨𝐩}$ was to characterise types with no computational meaning with the intention that terms of such types could be erased upon extraction. However, the assumption that every element of $\mathrm{𝐏𝐫𝐨𝐩}$ should be proof irrelevant has never been integrated to the system. Indeed, in Coq, proof irrelevance for the sort $\mathrm{𝐏𝐫𝐨𝐩}$ is not incorporated into the theory: it is only compatible with it, in the sense that its assumption does not give rise to an inconsistent theory. In fact, the exact status of the sort $\mathrm{𝐏𝐫𝐨𝐩}$ in Coq has never been entirely clarified, which explains in part this lack of integration. Homotopy type theory brings fresh thinking on this issue and suggests turning $\mathrm{𝐏𝐫𝐨𝐩}$ into the collection of terms that a certain static inference procedure tags as proof irrelevant. The goal of this task is to integrate this insight in the Coq system and to implement a definitional proof-irrelevant version of the sort $\mathrm{𝐏𝐫𝐨𝐩}$.

Extend the Coq proof assistant with a computational version of univalence

The univalence principle is becoming widely accepted as a very promising avenue to provide new foundations for mathematics and type theory. However, this principle has not yet been incorporated into a proof assistant. Indeed, the very mathematical structures (known as $\infty$-groupoids) motivating the theory remain to this day an active area of research. Moreover, a correct and decidable type checking procedure for the whole theory raises both computational complexity and logical coherence issues. Observational type theory [32], as implemented in Epigram, provides a first-stage approximation to homotopy type theory, but only deals with functional extensionality and does not capture univalence. Coquand and his collaborators have obtained significant results on the computational meaning of univalence using cubical sets [39], [45]. Bickford has initiated a promising formalisation work (http://www.nuprl.org/wip/Mathematics/cubical!type!theory/index.html) in the NuPRL system. However, a complete formalisation in intensional type theory remains an open problem.

Hence a major objective is to achieve a complete internalisation of univalence in intensional type theory, including an integration to a new version of Coq. We will strive to keep compatibility with previous versions, in particular from a performance point of view. Indeed, the additional complexity of homotopy type theory should not induce an overhead in the type checking procedure used by the software if we want our new framework to become rapidly adopted by the community. Concretely, we will make sure that the compilation time of Coq’s Standard Library will be of the same order of magnitude.

Extend the logical power of type theory without axioms in a modular way

Extending the power of a logic using model transformations (e.g., forcing transformation [71], [70] or the sheaf construction [100]) is a classic topic of mathematical logic [46], [76]. However, these ideas have not been much investigated in the setting of type theory, even though they may provide a useful framework for extending the logical power of proof assistant in a modular way. There is a good reason for this: with a syntactic notion of equality, the underlying structure of type theory does not conform to the structure of topos used in mathematical logic. A direct incorporation of the standard techniques is therefore not possible. However, a univalent notion of equality brings type theory closer to the required algebraic structure, as it corresponds to the notion of $\infty$-topos recently studied by Lurie [83]. The goal of this task is to revisit model transformations in the light of the univalence principle, and to obtain in this way new internal transformations in type theory which can in turn be seen as compilation phases. The general notion of an internal syntactical translation has already been investigated in the team [40].

Methodology: Extending type theory with different compilation phases

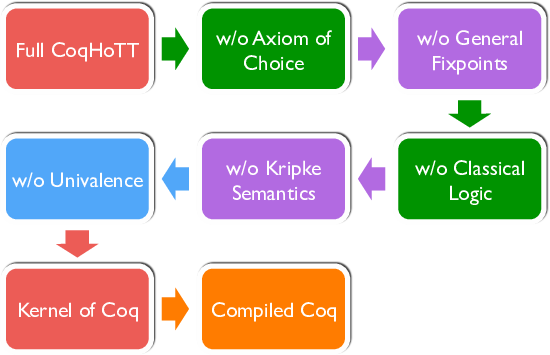
The Gallinette project advocates the use of distinct compilation phases as a methodology for the design of a new generation of proof assistants featuring modular extensions of a core logic. The essence of a compiler is the separation of the complexity of a translation process into modular stages, and the organization of their re-composition. This idea finds a natural application in the design of complex proof assistants (Figure 1). For instance, the definition of type classes in Coq follows this pattern, and is morally given by the means of a translation into a type-class free kernel. More recently, a similar approach by compilation stages, using the forcing transformation, was used to relax the strict positivity condition guarding inductive types [71], [70]. We believe that this flavour of compilation-based strategies offers a promising direction of investigation for the propose of defining a decidable type checking algorithm for HoTT.