Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.7. High performance computing
- A6.3.1. Inverse problems
- A6.5. Mathematical modeling for physical sciences
- A6.5.1. Solid mechanics
- A6.5.4. Waves
Other Research Topics and Application Domains
- B3. Environment and planet
- B3.3. Geosciences
- B3.3.1. Earth and subsoil
- B4. Energy
- B4.1. Fossile energy production (oil, gas)
- B5.2. Design and manufacturing
- B5.5. Materials
- B5.7. 3D printing
- B9.2.1. Music, sound
- B9.5.2. Mathematics
- B9.5.3. Physics
1 Team members, visitors, external collaborators
Research Scientists
- Hélène Barucq [Team leader, Inria, Senior Researcher, HDR]
- Juliette Chabassier [Inria, Researcher]
- Julien Diaz [Inria, Senior Researcher, HDR]
- Augustin Ernoult [Inria, Researcher, from Oct 2020]
- Titly Farhana Faisal [Inria, Starting Research Position]
- Ha Howard Faucher [Inria, Researcher]
- Papa Mangane [Inria, Starting Research Position, until Mar 2020]
- Yder Masson [Inria, Starting Research Position, until Oct 2020]
Faculty Members
- Marc Duruflé [Institut National Polytechnique de Bordeaux, Associate Professor]
- Sébastien Tordeux [Univ de Pau et des pays de l'Adour, Associate Professor, HDR]
Post-Doctoral Fellows
- Augustin Ernoult [Inria, until Sep 2020, funded by Conseil Régional de Nouvelle-Aquitaine]
- Tobias Van Baarsel [Inria, from Feb 2020]
PhD Students
- Guillaume Castera [Inria, from Oct 2020]
- Stefano Frambati [TOTAL-Pau]
- Alexandre Gras [Institut d'optique graduate school, until Sep 2020]
- Pierre Jacquet [Inria]
- Victor Martins Gomes [Univ de Pau et des pays de l'Adour, funded by E2S UPPA]
- Rose Cloe Meyer [Univ de Pau et des pays de l'Adour, funded by E2S UPPA]
- Nathan Rouxelin [Univ de Pau et des pays de l'Adour, funded by E2S UPPA]
- Chengyi Shen [Univ de Pau et des pays de l'Adour, until May 2020]
- Margot Sirdey [ONERA]
- Alexis Thibault [Univ de Pau et des pays de l'Adour, from Sep 2020]
- Vinduja Vasanthan [Inria]
Technical Staff
- Aurelien Citrain [Inria, Engineer]
- Olivier Geber [Inria, Engineer, from Oct 2020]
- Chengyi Shen [Inria, Engineer, from Jun 2020, funded by FEDER-POCTEFA]
Interns and Apprentices
- Anais Binet [Inria, until Jan 2020]
- Yolan Levrero [Ministère de l'Education Nationale, Feb 2020]
- Alexis Thibault [École Normale Supérieure de Paris, until Feb 2020]
Administrative Assistant
- Sylvie Embolla [Inria]
Visiting Scientist
- Mounir Tlemcani [Université des Sciences et de la Technologie d'Oran - Mohamed Boudiaf, Mar 2020]
2 Overall objectives
Numerical geosciences encompass a large variety of scientific activities tackling societal challenges like water resources, energy supply, climate change, etc. They are based upon observations, physical modeling and accurate mathematical formulations. The tremendous progresses of scientific computing have allowed the addition of extensive numerical simulations which provide tools based on wave measurements to study and possibly monitor complex environments that are otherwise difficult to probe and even fathomless e.g. the subsurface or the interior of stars.
Bridging the gap between experimental measurements and numerical simulations is an important objective of Magique-3D, which pursues a balance between accuracy and efficiency depending on the application domains in consideration. A common strategy will be to develop frugal models using mathematical methods (asymptotical methods, artificial boundary conditions, reduction methods…), and efficient numerical schemes (in both time and harmonic domains, using analytical and high order numerical methods).
Magique-3D research program is to develop numerical software packages for retrieving shapes and/or physical properties of complex media with a particular focus on the Earth and its natural reservoirs. An outstanding goal will consist in coupling seismic wave propagation with other physics in order to improve the knowledge of natural reservoirs which complex definition requires using high-resolution imaging techniques. The underlying models involves a genuinely larger number of parameters, and in order to take them into account, it is necessary to build models that are simplified but just as accurate, however easier to solve numerically. For this, Magique-3D collaborates with experimental geophysicists who help to assess the impact of parameters on the wave propagation.
In addition to geophysical setting, Magique-3D research program has enlarged its application range by addressing two other topics: solar imaging and musical acoustics. For solar imaging, modeling is of great importance and requires working with new equations in an equally new mathematical formalism. This also leads to the need of developing simulation codes with a long-term view to solve inverse problems. Given the similarities that exist between seismic and solar imaging methods, software development is carried out in-house using many of the skills acquired by the team in geophysical imaging. Regarding modeling of musical instruments, the size of the objects and the wavelengths considered are different from geophysical or solar contexts, but similar physical principles and theoretical aspects of models and numerical methods are applicable. Last but not least, parameter reduction and great precision required in the simulation and the possibility to easily compare numerical and experimental data make them an ideal topic to develop new research related to modeling and simulating wave propagation.
To address the above research agenda, Magique-3D gathers applied mathematicians and acousticians who have long working experience in wave propagation. The team is jointly shared by the University of Pau and Pays de l’Adour (UPPA) and Inria. The majority of Magique-3D members are located in Pau. The team is therefore attached to LMAP (Mathematics and Applications Laboratory in Pau, UMR CNRS 5142). However, some members of the team are located in Talence, in the Inria building of the Bordeaux campus. The choice of Magique-3D's principal location in Pau is fully justified by the long-term involvement of the city of Pau in Geosciences, which offers an important network of companies working in the geo-resources sector. In particular, the company Total is our main industrial partner with whom we aim at developing new numerical methods for energy transition.
Magique-3D relies on strong collaborations and partnerships with various institutions including (a) local industry (TOTAL, RealTimeSeismic), (b) national research centers (ONERA), and (c) international academic partnerships (e.g. Interdisciplinary Research Institute for the Sciences (IRIS) at California State University, Northridge, USA; University of Pays Basque and Basque Center of Applied Mathematics at Bilbao, Spain; University of California at Berkeley, Lawrence Berkeley National Laboratory, Max Planck Institute at Göttingen).
3 Research program
Magique-3D organizes its research program from in-house accurate solution methodologies for simulating wave propagation in realistic scenarios to various applications involving transdisciplinary efforts. Performing simulations of real-world phenomena is an ultimate endeavor by all numerical scientists. To achieve this, one needs real data and advanced mathematical models and high-order numerical schemes that are compatible with high-performance computing architectures.
To obtain real data, in addition to its current collaborations with scientists both from Academia and Industry, Magique-3D is developing a new branch of research activities by carrying out its own laboratory measurements. The desire to carry out its own measurements is motivated by the need to solve problems whose increasing complexity involves a large number of physical parameters that need to be calibrated. For instance, in order to take into account porosity, parameters such as viscosity, attenuation, thermodynamic effects, etc., must be integrated, and their impact must be properly analyzed before considering using them to characterize the propagation media. This constitutes a clear step ahead for Magique-3D , and opens up new prospects of contributing to the characterization of very complex media based on wave field measurements.
Regarding the development of numerical schemes, Magique-3D is developing high-order Discontinuous Galerkin (DG) methods and high-order time schemes. Recently, the team has launched a new research project on space-time integration for seismic waves, in partnership with Total. The coupling of DG methods with other techniques of discretization is also under consideration. Trefftz-DG and Hybridizable DG methods are currently developed both for poro-elastic waves and electromagnetic waves. HDG and HDG+ formulations are also under study for helioseismology.
The research activities of members of Magique-3D share a common theme of using numerically computed wavefield measurements to reconstruct the propagation medium they passed through before recording. The medium can be reconstructed by identifying either the physical parameters or the geometrical parameters that characterize it. In each case, the next step is to solve an inverse problem that is non-linear and ill-posed. To solve it, Magique-3D is focusing on the Full Waveform Inversion (FWI), which is a high-definition imaging method widely used in the field of geophysics.
4 Application domains
Magique-3D research program is organized around three principal domains of applications: geophysical exploration, solar imaging, and music. Each of them requires a relevant panel of significant contributions requiring achievements in laboratory measurements, modeling, mathematical analysis, advanced numerical schemes and massively parallel software development. Experimental research is a new activity that will ensure the team to have its own set of real data in addition to those provided by its partners. Magique-3D's application domains can be regrouped into a long-standing activity dedicated to subsurface imaging, and two more recent activities dedicated to solar imaging and the development of numerical wind instruments. Each field of application is not compartmentalized in the methodological sense of the term: equations, numerical schemes and programming practices can be shared and then adapted to the application in question.
4.1 Geophysical exploration
Geophysical exploration is a historical field for the team (see e.g 36, 40, 41, 44.Geophysical exploration has been driven for a very long time by the goal of finding hydrocarbons. Today, it is evolving towards a very proactive direction in favor of renewable energies and Magique-3D commits part of its research activities in this direction. As a powerful tool for mapping the subsurface, seismic imaging is very useful in many applications like geothermal energy and injection of CO2.
These applications share the Full Waveform Inversion (FWI) as a solution methodology for reconstructing quantitatively the physical parameters from observed data. FWI can be carried out in time-domain 39, 62, 73, 74 or in frequency domain 67, 66, 65. Its main feature is to avoid the formation of the large Jacobian matrix by computing the gradient of the misfit functional using the adjoint-state method 46. A detailed review of FWI for geophysical applications can be found in 64.
4.1.1 Deep geothermal energy
Obtaining accurate images of natural reservoirs is still critical for their management and exploitation and seismic imaging is an efficient tool (see 61, 59 and their references therein. One example is with deep geothermal energy which requires precise imaging of deep fractured reservoirs filled with geothermal fluids. Standard seismic imaging is based upon inverting mechanical waves which have difficulties to detect them, whereas electromagnetic waves are more sensitive. We see here a clear interest of coupling seismic with electromagnetic methods and this is what Magique-3D is developing with the CHICkPEA project. This is a multidisciplinary project involving experimental geophysicists from UPPA, members of the LFCR (Laboratory of Complex Fluids and their Reservoirs) and Steve Pride, professor at the University of Berkeley, who developed the theory describing the coupling between seismic waves and electromagnetic waves called seismoelectric effects 68. CHICkPEA started in 2018 and it was scheduled to be completed at the end of 2021. However, beginning of 2021, the team will be involved in a new project SEE4GEO funded by ADEME, in the framework of Geothermica call http://
4.1.2 Shallow geothermal energy
Regarding shallow geothermal energy, Magique-3D has started a collaboration with RealTimeSeismic SME in the framework of the FEDER-Poctefa Pixil project in order to use surface waves for a better imaging of shallow reservoirs. This project goes further in the work carried out on the inversion of seismic waves. Surface waves have long been considered as noise in seismograms because they were used to study the subsurface at depths. In shallow geothermal energy, surface waves contain interesting information on the first layers of the subsurface. Inverting them is a real problem because the surface waves are of high amplitude while propagating slowly. They therefore pose difficulties for multi-frequency optimization methods. The analysis of surface wave properties derives from the analysis of elastic wave propagation in horizontally stratified media 75, 57, 60. Consequently, current surface inversion derives 1D property profiles from dispersion curves picked in the frequency-wavenumber domain 72. Most of the available methods are limited to only inverting the fundamental modes, while lateral variations are difficult to handle with this approach. To overcome these limitations, the academia community has recently started to apply Full Waveform Inversion to this specific problem 70, 63.
4.1.3 CO2 injection
The reduction of greenhouse gases in the atmosphere is a societal topic of the utmost importance, with the Paris Agreement setting ambitious goals for many countries. One fundamental pillar of greenhouse emission management is Carbon Capture Utilisation and Storage (CCUS) 76. With this strategy, carbon dioxide produced on- or off-site is sequestered and injected into depleted reservoirs, thus offsetting an important portion of current CO2 emissions. The successful and safe implementation of this strategy requires the prediction, monitoring and surveillance of stored CO2 over long periods, which presents significant challenges in terms of seismic acquisition, seismic inversion and numerical simulation. These tools, coupled with state-of-the-art flow simulations, are vital in order to support the injection operations with vital real-time and long-term information. Moreover, specific challenges related to the physics of injected CO2, such as viscosity, temperature and multi-phase fluid conditions push to the limits our current numerical models, and require ambitious new multi-physics simulations to support safe and cost-effective CO2 injection operations. For example, some recent publications like 71, 79 have shown that the combination of CO2-brine flow with wave propagation provides efficient simulations for the monitoring of sequestered CO2. Magique-3D proposes to develop numerical methods for this new application, in collaboration with Total, in the framework of the research agreement DIP (Depth Imaging Partnership).
4.2 Solar imaging
The Sun sustains various types of waves which are driven by near-surface turbulent convection. These movements can be observed at the surface by the Dopplergrams given by ground-based or satellite-borne observatories. In recent years, methods for understanding Earth subsurfaces have opened up new ways to study the interior of the Sun as in the case with helioseismology and the interior of stars with aesteroseismology from oscillation observed at their surface. Techniques in helioseisomolgy is generally divided into global and local helioseismology. The first approach studies frequencies of oscillations modes, cf. 42, 47. This is also the current strategy of asteroseismology, cf 58, 34, 35. On the other hand, local helioseimology which adapts techniques of geophysical seismic interferometry studies, measure local wave propagation and works with the full 3D observed wavefield, and is thus more adapted to study additional features such large-scale flows in active region, sun spots and plage, cf. 54, 53.
With its long-run expertise in numerical tools for imaging Earth subsurfaces,
Magique-3D is extending its activity on terrestrial seismology to studying the Sun, for the latter offers a vast wealth of problems to be explored both for direct modeling as well as inversion.
In this development, associated team ANTS (Advance Numerical meThods for helioSeismology was created in 2019 to formalize a collaboration with MPS (Max Planck institute for Solar research, https://
As a first result of the collaboration of Magique-3D with MPS, in 52, a new computational framework based on the scalar equation was developed and produces solar-like power spectra and time-distance diagrams under appropriate assumption of source excitation. A second topic under active research is boundary conditions that allow waves to propagate. This also plays a crucial point in forward modeling as well as inversion. There are two on-going directions to proceed.
- In a goal to create
power spectrum and time-distance diagram that are closer to real observable, we need to include important physical effects such as gravity, magnetic and rotation forces.
This requires extending the computation framework for scalar equation to vector equation.
In including the effect of gravity, one hopes to find g-modes on simulated power spectrum (currently missing from that associated with the scalar equation).
These above physics are also needed in order to study active regions of the sun such as Sunspots. Shallow layers of the Sun will be probed with more accuracy, which will be useful for the study of supergranulation.
This is topic, Magique-3D can benefit from discussion and collaboration with Inria teams such as TONUS team with their experience in simulating tokamak plasma for thermonuclear reaction
(http://
schnaps. gforge. inria. fr/). - On the other hand, with the current established framework for the scalar equation, the next step is to the inverse problem, in particular with time-distance helioseismology 45, 50 and holography 80, 55. Current state-of-the art tools in these references is linear inversion using Born approximation. In additional they are carried out in 1D or 2D. It is thus interesting to apply nonlinear inversion such as Full Waveform Inversion cf. 49 to these problems.
4.3 Musical acoustics
This field of application is a subject of study for which the team is willing to take risks. We propose using a mix of experimental and numerical approach in order to study and design musical instruments. Makers have designed wind musical instruments (as flutes, trumpets, clarinets, bassoons...) in the past through “trial and error” procedures by performing a geometrical calibration of musical instruments in order to improve their accuracy, tone, homogeneity and even their sound volume, ergonomics, and robustness. During the past few decades, musical acoustics has been in a process of rationalizing the empiric understanding of instrument makers in order to formulate a scientific approach to future evolution. Our research proposal is along this axis of research by proposing new mathematical models based on our solid experience in terms of wave propagation in media with interfaces that can significantly change the sound. As was done in geophysical exploration, we propose to assist the modelling process with laboratory experiments. Direct comparison between simulations and experiments will allow to assess the model error. For this purpose, an experimental device has been developed in collaboration with I2M, Mechanics Laboratory of the University of Bordeaux and Humeau Factory, Montpon- Ménestérol, and is currently in use.
4.3.1 Modeling
Although the playing context should always be the final reference, some aspects of the behavior of a wind instrument can be firstly characterized by its entry impedance which quantifies the Dirichlet-to-Neumann map of the wave propagation in the pipe in the harmonic domain. This impedance can be both measured 51, 48 and computed with simulations based on accurate and concise models of the pipe 69, 4377,13. A more realistic approach accounts for the embouchure 56, 43, 37, 38, 78, which is modeled as a nonlinear oscillator coupled with the pressure and acoustic velocity at the entry of the pipe, allowing to predict the sound qualities. Mathematical properties of the underlying models are not yet totally understood, and adequate models still need to be developed. This is particularly true when accounting for dissipation phenomena, junctions of pipes, pipe porosity and rugosity, embouchures...
To reproduce the sound of instruments, time-dependent models are more suitable. Here, nonlinear lumped elements induce an “auto-oscillatory” behavior of the instrument. The models currently available in the literature are meant to reproduce viscothermal effects, pipe junctions, pipe radiation, lips oscillation, etc. They do not necessarily possess adequate mathematical properties to ensure stable simulations and they should be improved using asymptotic analysis methods or Lagrangian formalism.
4.3.2 Numerical methods
As far as numerical developments are concerned, the accuracy of the calculations is essential. Indeed, for some aspects like the sounding frequency, a deviation of 1% between the predictions and the observations is unacceptable. Moreover, contrary to what the team is used to do for geophysics or astrophysics thanks to HPC, numerical methods for acoustical musics must be frugal to be run on personal computers by acousticians and makers. Magique-3D has a wide range of numerical methods that have been implemented in its codes for linear problems. New numerical schemes will have to be implemented to take into account the non-linearities of time-dependent models.
4.3.3 Virtual workshop
Beyond the idea of mathematically modeling musical instruments, Magique-3D wishes to develop a virtual workshop whose vocation will be twofold: (i) support the manufacturers to design new instruments; (ii) recreate the sound of old and historical instruments. To implement this idea, we propose to elaborate optimization techniques that are well-known in the team to define optimal geometries to meet given specifications. This can be used to reconstruct existing instruments from acoustic measurement or to design new instruments by fixing relevant quantitative objective which is a research activity by its own 14. Behind the idea of the virtual workshop is also the intention to hear the instruments, from the knowledge of their shape and playing regime. For that purpose, time-domain models are essential.
5 Social and environmental responsibility
5.1 Footprint of research activities
Since March 2020, the team no longer travels abroad. However, it has not slowed down its international collaborations. It is therefore a forced and interesting experience that shows us that we can, in the future, consider selecting our missions abroad to reduce our carbon footprint. We also continue to believe that it is important to meet our foreign collaborators to create real ties and solve certain problems that require us to put ourselves in front of a board. The year 2020 will have helped us begin this change in attitude.
All team members living within 10km of their workplace prefer to bike or walk to work. Others, when possible, prefer public transportation. It should be noted that the team members hosted in Pau do not benefit from the same conditions as those hosted in Talence: no shower at the workplace, the public transportation network is not very developed outside the city of Pau.
5.2 Impact of research results
The team has been working with Total since its creation. With them, it has developed algorithms to improve the imaging of the subsurface. For more than 10 years, subsurface imagery was carried out in support of geophysical exploration campaigns deployed to find oil and gas reservoirs. Today, the Total Group is engaged in a process of transformation towards green and renewable energies. With Total, the team is carrying out new algorithmic developments that are designed to be applied to CO2 injection and storage as well as geothermal energy.
Solving wave equations in complex media to simulate the propagation of several thousand sources is a classical problem in geophysical exploration. To achieve these direct simulations, it is still absolutely necessary to have a high computational power. Thus, even using the most advanced clusters, it is mandatory to reduce the computational loads to consider solving inverse geophysical problems. The team has therefore been working for a long time on the development of accurate numerical schemes, compatible with modern computer architectures and capable of pushing back the limits of simulations already carried out. Terrestrial and solar imaging is still awaiting advances in this field and the team will continue to contribute to this. However, the team has forged new partnerships for which access to supercomputers is not always possible, due to insufficient financial resources, or desired, because potential users only have a personal computer. This means that the team is also committed to an approach that promotes the use of reasonably energy-efficient computing resources.
Regarding the domain of wind musical instruments, an effort is made on model reduction in order to achieve frugal models that can be implemented on regular, not demanding infrastructure. The impact of this research is twofold. First it focuses on the development of a virtual workshop in order to help instrument makers quantify the consequence of a geometrical change without needing a prototype, therefore preventing tool making and material loss. Second, it aims at computing the sound of heritage musical instruments in a cultural purpose.
6 Highlights of the year
The team was privileged to recruit Augustin Ernoult, acoustician and wind instrument specialist as Inria's research fellow.
The team has formed a new partnership with Lawrence Livermore National Laboratory with whom it proposed a European project See4Geo to the call Geothermica 2020. This project has been accepted for a start date of January 1st, 2021.
We have made a major release of our openwind software.
6.1 Awards
Augustin Ernoult received the "Prix Yves Rocard 2020: prix jeune chercheur de la société française d'acoustique".
6.2 Covid impact on research activity
The year 2020 was marked by the covid crisis and its impact on society and its overall activity. The world of research was also greatly affected:
Faculty members have seen their teaching load increase significantly;
PhD students and post-docs have often had to deal with a worsening of their working conditions, as well as with reduced interactions with their supervisors and colleagues;
Most scientific collaborations have been greatly affected, with many international activities cancelled or postponed to dates still to be defined.
7 New software and platforms
7.1 New software
7.1.1 Hou10ni
- Keywords: 2D, 3D, Elastodynamic equations, Acoustic equation, Elastoacoustic, Frequency Domain, Time Domain, Discontinuous Galerkin
- Scientific Description: Hou10ni simulates acoustic and elastic wave propagation in time domain and in harmonic domain, in 2D and in 3D. It is also able to model elasto acoustic coupling. It is based on the second order formulation of the wave equation and the space discretization is achieved using Interior Penalty Discontinuous Galerkin Method. Recently, the harmonic domain solver has been extended to handle Hybridizable Discontinuous Galerkin Methods.
- Functional Description: This software simulates the propagation of waves in heterogeneous 2D and 3D media in time-domain and in frequency domain. It is based on an Interior Penalty Discontinuous Galerkin Method (IPDGM) and allows for the use of meshes composed of cells of various order (p-adaptivity in space).
- News of the Year: In 2020, we have implemented the 3D poroelastic equations and the coupling porelastic equations (poroelastic+electromagnetic) for the HDG formulation.
-
URL:
https://
team. inria. fr/ magique3d/ software/ hou10ni/ - Publications: hal-01513597, hal-01957131, hal-01388195, hal-01972134, hal-01957147, hal-02152117, hal-02486942, hal-02408315, hal-02911686, tel-03014772, hal-01656440, hal-01662677, hal-01623953, hal-01623952, hal-01513597, hal-01519168, hal-01254194, hal-01400663, hal-01400656, hal-01400643, hal-01313013, hal-01303391, hal-01408981, tel-01304349, hal-01184090, hal-01223344, hal-01207897, hal-01184111, hal-01184110, hal-01184107, hal-01207906, hal-01184104, hal-01207886, hal-01176854, hal-01408705, hal-01408700, tel-01292824, hal-01656440, hal-00931852, hal-01096390, hal-01096392, hal-01096385, hal-01096324, hal-01096318, tel-01133713, tel-00880628
- Authors: Julien Diaz, Elodie Estecahandy, Marie Bonnasse, Marc Fuentes, Rose-Cloé Meyer, Vinduja Vasanthan, Lionel Boillot, Conrad Hillairet
- Contact: Julien Diaz
- Participants: Conrad Hillairet, Elodie Estecahandy, Julien Diaz, Lionel Boillot, Marie Bonnasse, Marc Fuentes, Rose-Cloé Meyer, Vinduja Vasanthan
7.1.2 MONTJOIE
- Keywords: High order finite elements, Edge elements, Aeroacoustics, High order time schemes
- Scientific Description: Montjoie is designed for the efficient solution of time-domain and time-harmonic linear partial differential equations using high-order finite element methods. This code is mainly written for quadrilateral/hexahedral finite elements, partial implementations of triangular/tetrahedral elements are provided. The equations solved by this code, come from the ”wave propagation” problems, particularly acoustic, electromagnetic, aeroacoustic, elastodynamic problems.
- Functional Description: Montjoie is a code that provides a C++ framework for solving partial differential equations on unstructured meshes with finite element-like methods (continuous finite element, discontinuous Galerkin formulation, edge elements and facet elements). The handling of mixed elements (tetrahedra, prisms, pyramids and hexahedra) has been implemented for these different types of finite elements methods. Several applications are currently available : wave equation, elastodynamics, aeroacoustics, Maxwell's equations.
-
URL:
https://
gitlab. inria. fr/ durufle/ montjoie - Authors: Marc Durufle, Gary Cohen
- Contact: Marc Durufle
- Participants: Juliette Chabassier, Marc Durufle, Morgane Bergot
7.1.3 OpenWind
- Name: Open Wind Instrument Design
- Keywords: Wave propagation, Inverse problem, Experimental mechanics, Time Domain, Physical simulation
- Scientific Description: implementation of first order finite elements for wind musical instrument simulation. implementation of the Full Waveform inversion method for wind musical instrument inversion. implementation of energy consistent numerical schemes for time domain simulation of valve-type wind musical instrument.
- Functional Description: Simulation and inversion of wind musical instruments using one-dimensional finite element method with tonholes and fingering chart. The software has three functionnalities. First, the software takes the shape of a wind instrument and computes the acoustical response (answer to a given frequential excitation). Second, the software takes the instrument shape and the control parameters of a musician, and computes the produced sound and the time evolution of many acoustical quantities. Last, the software takes a measured acoustical response and computes the corresponding instrument geometry (inner bore and tone holes parameters).
- Release Contributions: Inversion module and temporal module
-
URL:
https://
openwind. gitlabpages. inria. fr/ web/ - Publications: hal-02984478, hal-02996142, hal-03132474, hal-02917351, hal-02432750, hal-02019515, hal-01963674
- Authors: Robin Tournemenne, Juliette Chabassier, Alexis Thibault, Augustin Ernoult, Guillaume Castera, Tobias Van Baarsel, Olivier Geber
- Contacts: Juliette Chabassier, Alexis Thibault, Augustin Ernoult, Olivier Geber
- Participants: Juliette Chabassier, Augustin Ernoult, Alexis Thibault, Robin Tournemenne, Olivier Geber, Guillaume Castera, Tobias Van Baarsel
7.1.4 Gar6more2D
- Keywords: Validation, Wave propagation
- Functional Description: This code computes the analytical solution of problems of waves propagation in two layered 3D media such as- acoustic/acoustic- acoustic/elastodynamic- acoustic/porous- porous/porous,based on the Cagniard-de Hoop method.
- News of the Year: In 2020, we have added the elasto/poroelastic coupling.
-
URL:
https://
gitlab. inria. fr/ jdiaz/ gar6more2d - Publications: inria-00274136, inria-00404224, inria-00305395
- Contacts: Julien Diaz, Abdelaâziz Ezziani
- Participants: Abdelaâziz Ezziani, Julien Diaz
- Partner: Université de Pau et des Pays de l'Adour
7.1.5 Utmodeling
- Name: Time-domain Wave-equation Modeling App
- Keywords: 2D, 3D, Elastoacoustic, Elastodynamic equations, Discontinuous Galerkin, Time Domain
- Scientific Description: tmodeling-DG simulate acoustic and elastic wave propagation in 2D and in 3D, using Discontinuous Galerkin Methods. The space discretization is based on two kind of basis functions, using Lagrange or Jacobi polynomials. Different kinds of fluxes (upwind and centered) are implemented, coupled with RK2 and RK4 time schemes.
- Functional Description: tmodelling-DG is the follow up to DIVA-DG that we develop in collaboration with our partner Total. Its purpose is more general than DIVA-DG and should contains various DG schemes, basis functions and time schemes. It models wave propagation in acoustic media, elastic (isotropic and TTI) media and elasto-acoustic media, in two and three dimensions.
- News of the Year: In 2020, the major addition comes from the implementation of the Spectral Element method to simulate wave propagation in acoustic media meshed with structured quadrilateral meshes. We had in particular to adapt the existing spectral element codes (including the one developed in Aurélien Citrain's PhD thesis) to the structure of the utModeling code developed mainly for Discontinuous Galerking method.
- Contacts: Julien Diaz, Hélène Barucq
- Participants: Julien Diaz, Lionel Boillot, Simon Ettouati, Hélène Barucq, Aurelien Citrain
- Partner: TOTAL
7.1.6 utFWI
- Name: Unstructured Time Domain Full Waveform Inversion
- Keywords: Discontinuous Galerkin, Inverse problem, Acoustic equation, 2D, Time Domain
- Functional Description: utFWI is developed in collaboration with Total within the framework of DIP (Depth Imaging Partnership). The aim is to solve the problem of seismic imaging using the FWI (Full Waveform Inversion) method in the time domain on unstructured meshes, in particular using Galerkin Discontinuous methods. The objective is to characterize the physical properties of the considered medium by iteratively solving a minimization problem. The direct problem is simulated using Galerkin Discontinuous elements. The reconstruction of the physical parameters is carried out using gradient descent methods. The Solver works with the acoustic equation.
- News of the Year: In 2020, we have fully validated the 2D case. We have implemented the 3D case, and completed the validation on toy examples. The validation on realistic model is on going. We have implemented new features : WADG (Weight Adjusted Discontinuous Galerkin methods) and adaptive meshing.
- Contacts: Julien Diaz, Pierre Jacquet, Hélène Barucq
- Participants: Pierre Jacquet, Julien Diaz, Hélène Barucq
8 New results
8.1 Analytical and experimental solutions for validation
8.1.1 Analytical solutions for elasto/poroelastic coupling
Participants: Julien Diaz.
Our software Gar6more computes the analytical solution of waves propagation problems in 2D homogeneous or bilayered media, based on the Cagniard-de Hoop method. In the bilayered case, we had implemented the following coupling: acoustic/acoustic, acoustic/elastic, acoustic poroelastic, elastic/elastic, poroelastic/poroelastic. In the frame work of collaboration with Peter Moczo (Comenius University Bratislava and Slovak Academy of Sciences) and David Gregor (Comenius University Bratislava), we have implemented the coupling between elastic and poroelastic media.
8.1.2 Experimental solutions for seismic/electromagnetic coupling
Participants: Hélène Barucq, Victor Gomes Martins.
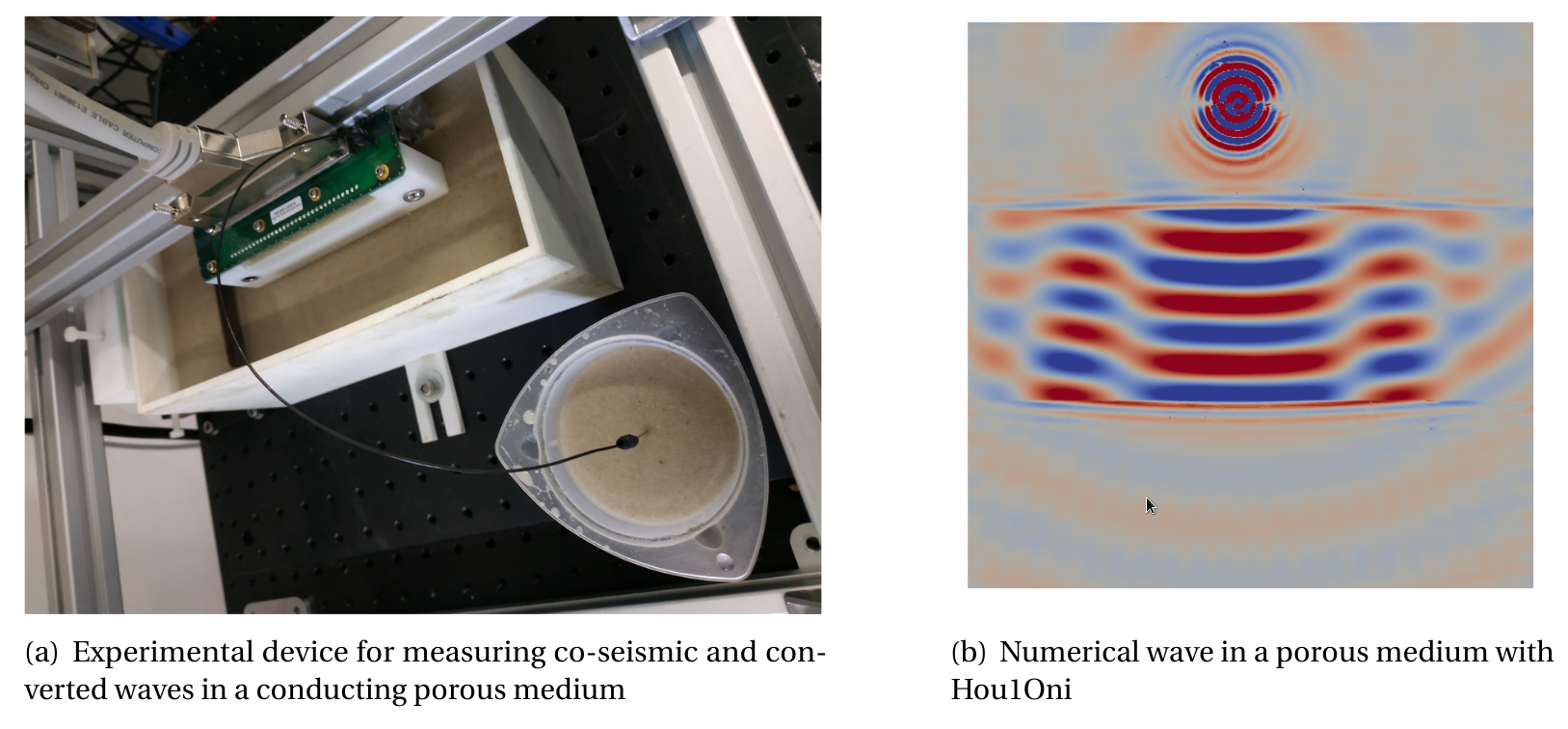
Obtaining accurate images of water, mineral and energy sources deep below the surface is critical for their management and exploitation. Seismic imaging allows for obtaining maps of the Earth’s interior and can be improved by coupling seismic and electromagnetic waves. Seismo-electric effects have been highlighted by Pride theory which yields equations combing Biot’s equations describing waves in porous media with Maxwell equations. The question of reproducing seismo-electric coupling in laboratory is very interesting for two main reasons: (1) measurements the co-seismic and converted wave are used for confirming the theory; (2) measurements in laboratory consist of a set of data that can be used in numerical experiments and provide a way for validating simulations.
Laboratory experiments are now operational and produce high-resolution data sets of direct and converted seismic and mechanical waves. We have been working on instrumentation for saturated sand experiments to improve the signal-to-noise ratio. We have also adopted an approach to ensure the repeatability of the measurements. The instrumental and methodological developments open perspectives for systematic parametric studies (salinity and saturation of the porous medium, thickness and nature of the porous interface) unique and very original. The prospect of quantitatively characterizing in the laboratory the converted seismo-electric wave in terms of morphology and intensity remains the major objective of the experimental approach with the ultimate goal of applying these advances to field geophysics. Besides having high-definition data, we aim now at comparing experimental solutions with numerical ones. This work is done in collaboration with Daniel Brito from LFCR, UPPA.
8.1.3 Acoustic Impedance Measurements
Participants: Juliette Chabassier, Augustin Ernoult.
An impedance sensor has been built to give the possibility to compare the simulation results of the wave propagation into wind instruments to experimental data. Several techniques exist to measure the input impedance defined as the ratio of the acoustic pressure over the acoustic flow in the frequential domain at the entrance of the wind instrument (or any pipes). The sensor developed in collaboration with Samuel Rodriguez is based on the "two microphones, three calibrations" method. The sensor is composed of a cylindrical pipe along which are placed five microphones, each couple being associated to different frequency range. At one extremity a loudspeaker emits a chirp, and the measured object is placed at the other extremity. The designed sensor has been built by Augustin Humeau in its workshop. Different pipes have been used as standards to validate the tools. The measuring bench can measure impedance from 40Hz to 10kHz with a good accuracy in a silent environment as the one given by the soundproof room recently acquired by BSO-research Center of Inria. Experimental data have been compared to simulation results and are used in full waveform inversion process to reconstruct the geometry of musical instruments. The presence of the five microphones gives us also the possibility to improve the reconstruction process by using directly the measured signal at the five observation points without computing the impedance. This work has been done in collaboration with Robin Tournemenne (alumni), Samuel Rodriguez (I2M) and Augustin Humeau (workshop Humeau).
8.2 Mathematical modeling
8.2.1 Nonuniqueness of the quasinormal mode expansion of electromagnetic Lorentz dispersive materials
Participants: Marc Duruflé, Alexandre Gras.
Any optical structure possesses resonance modes, and its response to an excitation can be decomposed onto the quasinormal and numerical modes of a discretized Maxwell operator. In this paper, we consider a dielectric permittivity that is an N-pole Lorentz function of the frequency. Even for discretized operators, the literature proposes different formulas for the coefficients of the quasinormal-mode expansion, and this comes as a surprise. We propose a general formalism, based on auxiliary fields, which explains why and evidences that there is, in fact, an infinity of mathematically sound possible expansion coefficients. The nonuniqueness is due to a choice of the linearization of Maxwell’s equations with respect to frequency and of the choice of the form of the source term. Numerical results validate the different formulas and compare their accuracy. This work has been done in collaboration with Philippe Lalanne (Bordeaux INP - Institut Polytechnique de Bordeaux and LP2N - Laboratoire Photonique, Numérique et Nanosciences) and is published in 19.8.2.2 Improvement of the modal expansion of electromagnetic fields through interpolation
Participants: Marc Duruflé, Alexandre Gras.
We consider optical structures where the dielectric permittivity is a rational function of ω (Lorentz model). Electromagnetic fields can be computed for a large number of frequencies by calculating the eigenmodes of the optical device and by reconstructing the solution by developing it on these modes. This modal development suffers from many limitations that are detailed in 30. In order to overcome these limitations, an interpolation procedure is proposed so that the electric field is computed directly for a small number of interpolation points. Numerical experiments in 2-D and 3-D show the efficiency of this approach. This work has been done in collaboration with Philippe Lalanne (Bordeaux INP - Institut Polytechnique de Bordeaux and LP2N - Laboratoire Photonique, Numérique et Nanosciences).
8.2.3 Equivalent multipolar point-source modeling of small spheres for fast and accurate electromagnetic wave scattering computations
Participants: Sébastien Tordeux.
We develop reduced models to approximate the solution of the electromagnetic scattering problem in an unbounded domain which contains a small perfectly conducting sphere. Our approach is based on the method of matched asymptotic expansions. This method consists in defining an approximate solution using multi-scale expansions over outer and inner fields related in a matching area. We make explicit the asymptotics up to the second order of approximation for the inner expansion and up to the fifth order for the outer expansion. We validate the results with numerical experiments which illustrate theoretical orders of convergence for the asymptotic models requiring negligible computational cost. This work has been published in 20 and was done in collaboration with Justine Labat from CEA Cesta and Victor Péron from LMAP, UPPA.8.2.4 Extension of the Gunter derivatives to Lipschitz domains and application to the boundary potentials of elastic wavesJournal of Applied Mechanics and Technical Physics
Participants: Sébastien Tordeux.
Regularization techniques for the trace and the traction of elastic waves potentials previously built for regular domains are extended to the Lipschitz case. In particular, this yields an elementary way to establish the mapping properties of elastic wave potentials from those of the scalar Helmholtz equation without resorting to the more advanced theory for elliptic systems in the Lipschitz domains. Representations of the Gunter operator and potentials of single and double layers of elastic waves in the two-dimensional case are provided. This work has been published in 12 This is a joint work with Yuriy Matveevich Volchkov and Abderrahmane Bendali.
8.2.5 Asymptotic behavior of acoustic waves scattered by very small obstacles
Participants: Hélène Barucq, Julien Diaz, Sébastien Tordeux.
The direct numerical simulation of the acoustic wave scattering created by very small obstacles is very expensive, especially in three dimensions and even more so in time domain. The use of asymptotic models is very efficient and the purpose of this work is to provide a rigorous justification of a new asymptotic model for low-cost numerical simulations. This model is based on asymptotic near-field and far-field developments that are then matched by a key procedure that we describe and demonstrate. We show that it is enough to focus on the regular part of the wave field to rigorously establish the complete asymptotic expansion. For that purpose, we provide an error estimate which is set in the whole space, includingthe transition region separating the near-field from the far-field area. The proof of convergence is established through Kondratiev’s seminal work on the Laplace equation and involves the Mellin transform. Numerical experiments including multiple scattering illustrate the efficiency of the resulting numerical method by delivering some comparisons with solutions computed with a finite element software. This work has been published in 8. It was done in collaboration with Vanessa Mattesi from Liège University.8.2.6 Outgoing solutions for the scalar wave equation in helioseismology
Participants: Hélène Barucq, Ha Pham.
In this work, we study the time-harmonic scalar equation describing the propagation of acoustic waves in the Sun's atmosphere under ideal atmospheric assumptions. We use the Liouville change of unknown to conjugate the original problem to a Schrödinger equation with a Coulomb-type potential. This transformation makes appear a new wavenumber, k, and the link with the Whittaker's equation. We consider two different problems: in the first one, with the ideal atmospheric assumptions extended to the whole space, we construct explicitly the Schwartz kernel of the resolvent, starting from a solution given by Hostler and Pratt in punctured domains, and use this to construct outgoing solutions and radiation conditions. In the second problem, we construct exact Dirichlet-to-Neumann map using Whittaker functions, and new radiation boundary conditions (RBC), using gauge functions in terms of k. The new approach gives rise to simpler RBC for the same precision compared to existing ones. The robustness of our new RBC is corroborated by numerical experiments. This work was started in 2019, and results in an article 11 published in 2020. This work was done in collaboration with Florian Faucher from Vienna University.
8.2.7 Outgoing solution and Radiation boundary condition for spherical Galbrun equation
Participants: Hélène Barucq, Ha Pham.
In this project, we consider the time-harmonic Galbrun’s equation under spherical symmetry in the context of the wave propagation in the Sun without flow and rotation, and neglecting the perturbations to the gravitational potential. For this equation, we construct the outgoing modal solutions, the 3D Green’s kernel, and radiation boundary conditions. The construction is justified by indicial and asymptotic analysis of the modal radial ODE. Our asymptotic analysis makes appear the correct wavenumber and the high-order terms of the oscillatory phase function, which we use to characterize outgoing solutions. The radiation boundary conditions are built for the modal radial ODE and then derived for the initial equation. We approximate them under different hypothesis and propose some formulations that are independent of the horizontal wavenumber and can thus easily be applied for 3D problems. The results are documented in the Inria report 28. We also prepared an article and submitted to Journal of Differential Equations.
This works also requires the construction of C2 representations of the background quantities that characterize the interior of the Sun and its atmosphere starting from the data-points of the standard solar model S. The constructed models are documented in 32. These works were done in collaboration with Florian Faucher from Vienna University, and Damien Fournier and Laurent Gizon from MPS.
8.2.8 Radiation boundary conditions for wave problems based upon Calderon operators
Participants: Hélène Barucq, Ha Pham.
We construct radiation conditions by accurately modeling the propagation of a time-harmonic wave in the vicinity of an interface. This idea is not new and has been exploited in particular to construct radiation conditions for the Helmholtz equation by solving an Airy equation obtained as an approximation of the Helmholtz operator in the vicinity of the interface. In this project, a Calderon operator is constructed and exact radiation conditions are constructed. This work is ongoing, in collaboration with Olivier Lafitte from Montréal University.8.2.9 Modeling and simulation of the piano touch
Participants: Juliette Chabassier, Guillaume Castera.
In this PhD work, we develop physical models for the piano to understand the real influence of the pianist on the sound. Mechanical models [iMMC] will be paired with vibro-acoustical models [INRIA] to analyse the differences in sound depending on the pianist’s touch. We are currently working on the crucial contact between the hammer and the string(s) which links the piano action to its vibro-acoustical part. Friction at impact must be taken into account in order to transmit all forces to the string. It could influence the longitudinal vibrations of the string, and then the presence of some partials in the final sound. We also implement these models in c++ into the MONTJOIE software. We use energy-based numerical schemes to guarantee stability, and auxiliary variables to deal with nonlinear terms. This PhD is co-supervised with Paul Fisette (Univ. Cath. Louvain, Belgium).8.2.10 Physical based synthesis of heritage wind musical instruments
Participants: Juliette Chabassier, Augustin Ernoult, Tobias Van Baarsel.
The SYSIMPA project (Synthèse Sonore des Instruments de Musique du PAtrimoine) spans over two years and is carried out by a consortium made up of Inria, la Cité de la Musique-Philharmonie de Paris (CM-P), l'Institut Technologique Européen des Métiers de la Musique (ITEMM) in Le Mans, and le Centre Culturel et de Restauration des Musées de France (C2RMF). This project aims at studying ancient music wind instruments (in this case, natural trumpets from around 1900) to estimate their acoustic properties and to synthesise their sound. Also, a copy of one of the instruments will be made by a instrument maker. The role of Magique-3D is at the same time to coordinate the different teams involved in SYSIMPA, and to deal with the scientific computation and sound synthesis aspects. The CM-P gives access to the music instruments and provides expertise on conservation and impedance measurements. The C2RMF has the facilities to perform X-ray tomography on ancient instruments. Finally, ITEMM drives the instrument-making aspect thanks to its partnership with the Institut National des Métiers d'Arts (INMA).
Most of the tools required for the project have been developped during this first year. Ten natural trumpets have been selected for the study, and have been put through x-ray tomography. In the meantime, all the paper archives (approx.3500 documents) corresponding to the music instruments and their makers have been scanned by the CM-P, and might provide useful information about the instrument making and/or playing. These documents will eventually be put online and made available to the public. The C2RMF sent us the data from the X-ray tomography. We developped a code to automatically extract the bore of the instruments from the raw images. The geometry estimation has been compared with a physical measurement of the input impedance performed at the CM-P, and validates the whole procedure for the most of the instrument. The mouthpiece is still a challenging piece, as the width of the metal in this part is large compared to the inner bore ; a separate measurement of the mouthpiece is planned in early march 2021 using a silicone mould.
The scientific computation done by Magique-3D consists of two parts : first a frequential computation part aiming at calculating the acoustic characteristic of the resonator through the impedance ; second a temporal computation that couples the resonator with a vibration model describing the musician's lips. The computation is done using OpenWind, a software currently developped by the INRIA team. The frequential computation has been compared with impedance measurements done at the CM-P. The comparison shows satisfactory agreement between simulation and experiment. The temporal simulation is on-going work. The coupling between a source and a resonator is tricky and needs finely tuned parameters in order to reach the sustained oscillation regime. The parameters (i.e., stiffness and mass of the lips, mouth pressure, etc.) are constantly adapted by the musician while playing, but cannot be directly measured. We will therefore rather use the dynamic systems theory, applied to wind instruments, to estimate the right set of parameters. Linear Stability Analysis and Harmonic Balance are some of the techniques being explored. This work on temporal simulation will allow us to simulate the sound of the studied trumpets, based on physical models and data extracted from x-ray tomography.
This work is done in collaboration with Romain Viala (ITEMM); Clotilde Boust and Elsa Lambert (C2RMF) ; Thierry Maniguet, Marguerite Jossic, Rodolphe Bailly, Cécile Cecconi and Sebastian Kirsch (CM-P).
8.2.11 Modeling and simulation of acoustical and dissipative phenomena in wind instruments
Participants: Juliette Chabassier, Alexis Thibault.
This research has been centered around modeling and simulation of acoustical and dissipative phenomena in wind instruments. It has contributed to the new public version of OpenWInD, released in december 2020, by implementing a numerical scheme for acoustic wave propagation with viscothermal losses, as well as several other models (spherical waves, transfer matrices, radiation of a pulsating sphere), and by writing a tutorial for new users of the toolbox. Bibliography around porous effect inside the instrument body is currently under investigation.8.2.12 Viscothermal models for wind musical instrument
Participants: Juliette Chabassier, Alexis Thibault.
33 is a review of one-dimensional and three-dimensional models of linear acoustic propagation with viscothermal effects, with the intent of applying them to wind instruments. It includes the derivation of several models from the linearized Navier-Stokes equations. The differences between the models are evaluated numerically and related to the simplifying assumptions used in deriving each model.8.2.13 Dissipative time-domain 1D model for viscothermal acoustic propagation in wind instruments
Participants: Juliette Chabassier, Alexis Thibault.
An approximate 1D time-domain model of acoustic propagation with boundary layer losses is proposed, where all the physical parameters of the instrument as the bore shape or the wave celerity are explicit coefficients. The model depends on absolute tabulated constants which only reflect that the pipe is axisymmetric. It can be seen as a telegrapher's equations augmented by an adjustable number of auxiliary unknowns. A global energy is dissipated. A variational approximation is proposed along with numerical experiments and comparisons with other models. This work is under review by the Journal of the Acoustical Society of America.8.2.14 Time-domain simulation of a dissipative reed instrument
Participants: Juliette Chabassier, Alexis Thibault.
This work focuses on the time-domain models and numerical schemes implemented in the OpenWInD toolbox. Modular components may be assembled and simulated, with stability guaranteed through energy consistency. This has been communicated during the Forum Acusticum 2020 22.8.2.15 The virtual workshop OpenWinD : physical modeling assisting wind instrument makers
Participants: Juliette Chabassier, Augustin Ernoult, Olivier Geber, Alexis Thibault, Tobias Van Baarsel.
Our project develops the software OpenWInD for wind instrument making. A first feature is the prediction of the acoustical response of the instrument from the knowledge of its shape (bore and holes). This can be done in the harmonic (impedance computation) and temporal (sound computation) domains. It can account for various physical situations (non constant temperature, coupling with an embouchure...). Discretization is done in space with 1D spectral finite elements and in time with energy consistent finite differences. The second feature is the reconstruction of the shape of an instrument that fulfils a certain objective. This can be used for bore reconstruction, and instrument design. The latter is based on a strong interaction with makers and musicians, aiming at defining interesting design parameters and objective criteria, from their point of view. After a quantitative transcription of these criteria, under the form of a cost function and a design parameter space, we implement various gradient-based optimization techniques. More precisely, we exploit the fact that the sound waves inside the instruments are solution to acoustic equations in pipes, which gives us access to the Full Waveform Inversion technique (FWI) where the gradient is characterized as the solution to another wave equation. The computational framework is flexible (in terms of models, formulations, coupling terms, objective functions...) and offers the possibility to modify the criterion by the user. The goal is to proceed iteratively between the instrument makers and the numerical optimisation tool (OpenWInD) in order to achieve, finally, criteria that are representative for the makers. This modeling tool give us the possibility to perform and analyze comparisons between measurements and simulation on real instruments in order to complete the model until to reach good enough accuracy to help the manufacturers in the design of new instruments. It has been presented at the conference Forum Acusticum 2020 23. This work has been done in collaboration with Robin Tournemenne (alumni) and Augustin Humeau (workshop Humeau).
8.3 High-order numerical methods for time-dependent problems
8.3.1 Tent Pitcher algorithm for space-time integration of wave problems
Participants: Hélène Barucq, Julien Diaz, Vinduja Vasanthan.
This thesis started on October 1st, 2019. Its objective is to develop a Trefftz-DG-Tent-Pitching formulation equipped with local-time stepping and outgoing boundary conditions in a full parallel environment constructed on unstructured nD+time meshes. A first formulation constructed on structured meshes and tested for toy examples has been given in E. Shishenina’s thesis. The first year of the PhD has been mostly devoted to bibliography on :
- Trefftz & boundary element methods,
- Different kinds of variational formulations (i.e Trefftz-Discontinuous Galerkin, Trefftz-Least Squares, Method of Fundamental Solutions, Ultra Weak Variational Formulation, Variational Theory of Complex Rays, Wave Based Method, etc),
- Different kinds of basis (Generalized Harmonic Polynomials,Plane Waves, fundamental solutions & multipoles, etc),
- Tent Pitcher algorithm.
Based on this, we also derived new formulations with another type of fundamental solutions as basis. This lead us to introduce alternative Absorbing Boundary Conditions applied to our problem.
In parallel, we ported the Matlab code to Fortran.
8.3.2 Construction and convergence analysis of conservative second order local time discretisation for linear wave equations
Participants: Juliette Chabassier.
In this work we present and analyse a time discretisation strategy for linear wave equations based on domain decomposition that aims at using locally in space the most adapted time discretisation among a family of implicit or explicit centered second order schemes. The proposed family of schemes is adapted to domain decomposition methods such as the mortar element method. They correspond respectivelyin that case to local implicit schemes and to local time stepping. We show that, if some regularity properties of the source termsolution are satisfied and if the time step verifies a stability condition, then the family of proposed time discretisations provides, in a strong norm, second order space-time convergence. Finally, we provide 1D numerical illustrations that confirm the obtained theoretical results and we compare our approach to other existing local time stepping strategies for wave equations. This work is under review 29. It is a collaboration with Sébastien Impériale from project-team M3DISIM.
8.3.3 High-order locally A-stable implicit schemes for linear ODEs
Participants: Hélène Barucq, Marc Duruflé, Mamadou N'Ddiaye.
Accurate simulations of wave propagation in complex media like Earth subsur-face can be performed with a reasonable computational burden by using hybrid meshes stuffing fine and coarse cells. Locally implicit time discretizations are then of great interest. They indeed allow using unconditionally stable schemes in the regions of computational domain covered by small cells. The receivable values of the time step are then increased which reduces the computational costs while limiting the dispersion effects. In this work we construct a method that combines optimized explicit schemes and implicit schemes to form locally implicit schemes for linear ODEs, including in particular semi-discretized wave problems that are considered herein for numerical experiments. Both the explicit and implicit schemes used are one-step methods constructed using their stability function. The stability function of the explicit schemes are computed by maximizing the time step that can be chosen. The implicit schemes used are unconditionally stable. The performance assessment we provide shows a very good level of accuracy for locally implicit schemes. It also shows that locally implicit scheme is a good compromise between purely explicit and purely implicit schemes in terms of computational time and memory usage. This work has been published in 9.8.4 High-order numerical methods for time-harmonic problems
8.4.1 A discontinuous Galerkin Trefftz type method for solving the two dimensional Maxwell equations
Participants: Margot Sirdey, Sébastien Tordeux.
Trefftz methods are known to be very efficient to reduce the numerical pollution when associated to plane wave basis. However, these local basis functions are not adapted to the computation of evanescent modes or corner singularities. In this article, we consider a two dimensional time-harmonic Maxwell system and we propose a formulation which allows to design an electromagnetic Trefftz formulation associated to local Galerkin basis computed thanks to an auxiliary Nédélec finite element method. The results are illustrated with numerous numerical examples. The considered test cases reveal that the short range and long range propagation phenomena are both well taken into account. This work has been published in 18 This is a joint work with Håkon Sem Fure and Sébastien Pernet.8.4.2 Numerical computation of Green function in helioseismology
Participants: Hélène Barucq, Ha Pham.
In this work, we provide an algorithm to compute efficiently and accurately the full outgoing modal Green's kernel for the scalar wave equation in local helioseismology under spherical symmetry. Due to the high computational cost of a full Green's function, current helioseismic studies rely on single-source computations. However, a more realistic modelization of the helioseismic products (cross-covariance and power spectrum) requires the full Green's kernel. In the classical approach, the Dirac source is discretized and one simulation gives the Green's function on a line. Here, we propose a two-step algorithm which, with two simulations, provides the full kernel on the domain. Moreover, our method is more accurate, as the singularity of the solution due to the Dirac source is described exactly. In addition, it is coupled with the exact Dirichlet-to-Neumann boundary condition, providing optimal accuracy in approximating the outgoing Green's kernel, which we demonstrate in our experiments. In addition, we show that high-frequency approximations of the nonlocal radiation boundary conditions can represent accurately the helioseismic products. This work results in 81-page Inria report 10 and article 10.
8.4.3 Low-order absorbing boundary condition for two-dimensional isotropic poroelasticity
Participants: Hélène Barucq, Julien Diaz, Ha Howard Faucher, Rose-Cloé Meyer.
In this work, we construct a low order absorbing boundary condition (ABC) for two-dimensional isotropic poroelasticity in frequency domain. The ABC is obtained for circular geometry by approximating the behavior of the analytical outgoing wave solution. The ABC is then extended to general non-circular domains and implemented with Hybridizable Discontinuous Galerkin (HDG) method. In circular symmetry, using the form of the exact solution, the robustness of the ABC is evaluated for the problem of scattering of planewave by a circular obstacle. We also compare the performance of this ABC with Perfectly Matched Layers, both coupled with HDG method. The results from this work are presented in Inria report 26. It is done in collaboration with Florian Faucher from Vienna University, and Damien Fournier and Laurent Gizon for MPS.8.4.4 Hybridizable Discontinuous Galerkin method for time-harmonic anisotropic poroelasticity in two dimensions.
Participants: Hélène Barucq, Julien Diaz, Ha Pham, Rose-Cloé Meyer.
In this work, we apply a Hybridizable Discontinuous Galerkin (HDG) method to numerically solve two-dimensional anisotropic poroelastic wave equations in the frequency domain given by Biot theory. The motivation for choosing HDG method comes from the complexity of the considered equations and the high number of unknowns. The HDG method possesses all the advantages of Discontinuous Galerkin method (hp-adaptivity, accuracy, ability to model complex tectonics,...) without a drastic increase in the number of degrees of freedom. We study the accuracy of the proposed method by comparisons with analytical solutions and a sensitivity analysis of the method as a function of stabilization parameters and frequency. We also show the ability of the method to reproduce the different types of poroelastic waves including the slow Biot wave on realistic geophysical media. Results on the HDG method for poroelasticity are presented in the research report 25, and in an article in preparation.8.4.5 HDG methods for the convected Helmholtz Equation.
Participants: Hélène Barucq, Nathan Rouxelin, Sébastien Tordeux.
The need for numerical simulation of harmonic waves propagating in complex flows arises in the context of computational helioseismology. As standard finite element methods do not perform well for those problems as they usually assume too much regularity on the solution, it seems natural to consider the use of discontinuous Galerkin methods. In order to obtain a method with a reduced numerical cost, we focus on a particular type of discontinuous Galerkin method : the so-called Hybridizable Discontinuous Galerkin method (HDG). The main feature of this method is the static condensation process, leading to an elimination of interior degrees of freedom and therefore to a problem posed only on the skeleton of the mesh.As those kinds of method have never been used for time-harmonic aeroacoustic wave propagation, we have started our work by considering the simplest aeroacoustic model : the convected Helmholtz equation. Even if this model can only be used in a very limited range of physical configurations, its study is a very important first step. Indeed, in contrary to other models, the natural framework for the study of the convected Helmholtz equation is clear and standard. We can therefore perform the numerical analysis of the method, leading to results on the local and global solvability of the method, as well as a detailed analysis of the convergence rate.
It is important to notice that in the process of designing a HDG method for the convected Helmholtz equation, we had to make some choices on both the unknowns of the method and the approximation spaces. We therefore chose to work on the three most natural choices to understand their different properties.
In the future, we hope to generalize our results and construct HDG methods for more realistic aeroacoustic models such as Galbrun’s or Goldstein’s equations.
8.4.6 Isogeometric analysis of sharp boundaries in full waveform inversion
Participants: Hélène Barucq, Julien Diaz, Stefano Frambati.
Efficient seismic full-waveform inversion simultaneously demands a high efficiency per degree of freedom in the solution of the PDEs, and the accurate reproduction of the geometry of sharp contrasts and boundaries. Moreover, it has been shown that the stability constant of the FWI minimization grows exponentially with the number of unknowns. Isogeometric analysis has been shown to possess a higher efficiency per degree of freedom, a better convergence in high energy modes (Helmholtz) and an improved CFL condition in explicit-time wave propagation, and it seems therefore a good candidate for FWI.
We have first focused on a small-scale one-dimensional problem, namely the inversion over a multi-step velocity model using the Helmholtz equation. By exploiting a relatively little-known connection between B-splines ad Dirichlet averages, we have added the knot positions as degrees of freedom in the inversion. We have shown that arbitrarily-placed discontinuities in the velocity model can be recovered using a limited amount of degrees of freedom, as the knots can coalesce at arbitrary positions, obviating the need for a very fine mesh and thus improving the stability of the inversion.
In order to reproduce the same results in two and three dimensions, the usual tensor-product structure of B-splines cannot be used. We have therefore turned our attention to the spaces of (unstructured) multivariate B-spline bases. In the first part of our work, we have uncovered a connection between unstructured polynomial-reproducing spline spaces and some objects known in combinatorial geometry as zonotopal tilings. Due to their purely combinatorial character, these spline spaces automatically cover the case of repeated and affinely dependent points, allowing to construct a broad family of splines with adjustable smoothness, up to (and including) discontinuities. This construction works in any number of space dimensions, and the mathematical properties of zonotopal tilings can be exploited to devise some practical algorithms for the construction and evaluation of these spline functions, useful in practical applications.
A research article containing these results has been submitted to the journal “Mathematics of Computation” in collaboration with Hélène Barucq, Julien Diaz and Henri Calandra. It is part of a 61-page long research report 24.
In the second part of our work, we have exploited the flexible regularity of our spline spaces in order to place internal boundaries into our simulation domains, decomposing them into multiple sub-domains of adjustable size. Adding standard IPDG fluxes between the subdomains then yields a very flexible numerical scheme that contains FEM, DG and (meshless) IGA as extreme cases, and allows to interpolate between them, offering a unifying perspective. The mass matrix obtained through our approach is block-diagonal, thus realizing a simple but powerful unstructured multi-patch DG-IGA hybrid, which is especially useful for time-explicit wave propagation simulations. A 2D simulation code was written on this premise, and numerical tests have been realized on synthetic datasets coming from applications in geoscience, helioseismic and musical instruments. Results have shown that the numerical advantages of IGA, notably the dependence of the CLF timestep on the polynomial order , are maintained, and good parallelizablility is achieved due to the block-diagonal mass matrix. Furthermore, each IGA domain is allowed to have an arbitrary topology, including any number of internal holes and boundaries, which can be especially interesting for the simulation and optimization of the acoustic properties of musical instruments.
These numerical results have been presented to the ECCOMAS 2020 congress (https://
Our efforts are currently focused on the realization of 3D numerical tests and the implementation of FWI inversion in 2D and 3D. A second journal article on the details of the unstructured multi-patch DG-IGA is in the works.
A research article has been submitted to Mathematical of Computation in collaboration with Hélène Barucq, Julien Diaz and Henri Calandra. It is part of a 61-page long research report 24. The numerical results have been presented to ECCOMAS 2020 congress (https://
This work is done in collaboration with Henri Calandra from Total.
8.5 Reconstruction and design using full waveform inversion
8.5.1 Time-Domain Full Waveform Inversion using advanced Discontinuous Galerkin methods
Participants: Hélène Barucq, Julien Diaz, Pierre Jacquet.
In this project, we developed tools for the reconstruction of subsurface media for seismic imaging and reservoir characterization in an industrial context. For that purpose, we used the Full Waveform Inversion (FWI) method. It is a reconstruction technique using data taken from seismic disturbances and whose behavior reflects the properties of the environment in which they propagate. In the framework of this thesis, we consider acoustic waves which are simulated thanks to Discontinuous Galerkin methods. These methods offer a very flexible discretization in space allowing to approach complex models and geometries. Discontinuous Galerkin methods are characterized by the use of fluxes in between each cell. Those fluxes contribute to have low communication costs which are highly recommended for High Performance Computing. Here, the wave equation is solved in time domain to overcome the memory limitations encountered in frequency domain for the reconstruction of large-scale 3D industrial media.
To reconstruct quantitatively the physical model under study, we wrote the inverse problem as a minimization problem solved by adjoint state method. This method makes it possible to obtain the gradient of the cost function with respect to the physical parameters for the cost of two simulations; the direct problem and the backward problem also called adjoint problem. The adjoint state will be the solution of the discretized continuous adjoint problem ("Optimize Then Discretize"). This choice is justified by a 1D comparison with the strategy which consists in "Discretize then Optimize" completed by an algebraic study in superior dimension. The gradient thus calculated, is a key in the optimization procedure developed and integrated in the industrial environment provided by the industrial partner, Total.
The propagator is a keystone in solving the inverse problem. Indeed, it is repeated successively and represents the majority of the computation time of the optimization process. It is therefore important to control the discretization by the Discontinuous Galerkin method as well as possible. In particular, in this thesis, we have considered the idea of using different polynomial bases of approximation (Legendre or Bernstein-Bézier) as well as the choice of the parameterization, which can either be constant per element or variable thanks to the use of the Weight Adjusted Discontinuous Galerkin (WADG) method. This last strategy offers the opportunity to enlarge the mesh cells without losing information on the model and thus allows a more advanced use of the -adaptivity that we propose to fully exploit thanks to an adaptive mesh that is adjusted to the model meant to evolve with the iterations of the inverse problem.
8.5.2 Full Waveform Inversion on data including surface waves
Participants: Hélène Barucq, Julien Diaz, Chengyi Shen.
This work is a part of the PIXIL project (Pyrenees Imaging eXperience: an InternationaL network). We aim at applying a Fortran HPC imaging tool, named HAWEN and developed by Florian Faucher in time-harmonic domain featuring the Hybridizable Discontinuous Galerkin method, onto real data. In particular, surface waves will be integrally taken into concern for the following reasons: first, the PIXIL project focuses on geophysical surveys for geothermal applications, where surface waves carry essential information of near-surfaces especially for shallow geothermal explorations; Second, a good image of the near-surface can help improve deep imaging. We looked into a 2D synthetic case study in order to establish one or several Multi-level Strategies for FWI on data including surface waves. A trade-off between robustness and high-resolution is achievable by elaborating suitable strategies such as combining asymptotic methods and FWI with frequency groups. Meanwhile, Bash and Python programs are created to assist HAWEN for user-friendly concerns as well as data pre/post-processing, for instance, automatization of executions, data processing and visualization. This is a joint work with Jean-Luc Boelle and Jean-Claude Puech from the SME Real Time Seismic.
8.5.3 Full reciprocity-gap waveform inversion enabling sparse-source acquisition
Participants: Hélène Barucq.
The quantitative reconstruction of subsurface earth properties from the propagation of waves follows an iterative minimization of a misfit functional. In marine seismic exploration, the observed data usually consist of measurements of the pressure field, but dual-sensor devices also provide the normal velocity. Consequently, a reciprocity-based misfit functional is specifically designed, and it defines the full reciprocity-gap waveform inversion (FRgWI) method. This misfit functional provides additional features compared to the more traditional least-squares approaches, in particular, in that the observational and computational acquisitions can be different. Therefore, the positions and wavelets of the sources from which the measurements are acquired are not needed in the reconstruction procedure and, in fact, the numerical acquisition (for the simulations) can be chosen arbitrarily. Based on 3D experiments, FRgWI is shown to behave better than full-waveform inversion in the same context. It allows for arbitrary numerical acquisitions in two ways: when few measurements are given, a dense numerical acquisition (compared to the observational one) can be used to compensate. However, with a dense observational acquisition, a sparse computational one is shown to be sufficient, for instance, with multiple-point sources, hence reducing the numerical cost. FRgWI displays accurate reconstructions in both situations and appears more robust with respect to crosstalk than least-squares shot stacking. This work has been done in collaboration with Florian Faucher (Vienna University), Giovanni Alessandrini (Faculty of Mathematics, Vienna), Maarten de Hoop (Rice University,Houston), Romina Gaburro (UL - University of Limerick) and Eva Sincich (University of Trieste). It has been published in 15.8.5.4 A priori estimates of attraction basins for velocity model reconstruction by time-harmonic Full Waveform Inversion and Data-Space Reflectivity formulation
Participants: Hélène Barucq.
The determination of background velocity by Full Waveform Inversion (FWI) is known to be hampered by the local minima of the data misfit caused by the phase shifts associated with background perturbations. Attraction basins for the underlying optimization problems can be computed around any nominal velocity model and guarantee that the misfit functional has only one (global) minimum. The attraction basins are further associated with tolerable error levels representing the maximal allowed distance between the (observed) data and the simulations (i.e., the acceptable noise level). The estimates are defined a priori, and only require the computation of (possibly many) first- and second-order directional derivatives of the (model to synthetic) forward map. The geometry of the search direction and the frequency influence the size of the attraction basins, and complex frequency can be used to enlarge the basins. The size of the attraction basins for the perturbation of background velocities in the classical FWI (global model parametrization) and the data-space reflectivity reformulation (MBTT) are compared: the MBTT reformulation increases substantially the size of the attraction basins (by a factor of four to fifteen). Practically, this reformulation compensates for the lack of low-frequency data. Our analysis provides guidelines for a successful implementation of the MBTT reformulation. This work has been done in collaboration with Florian Faucher (Faculty of Mathematics, Vienna), Guy Chavent (SERENA, Inria) and Henri Calandra (Total E&P) and has been published in 16.8.5.5 Eigenvector models for solving the seismic inverse problem for the Helmholtz equation
Participants: Hélène Barucq.
We study the seismic inverse problem for the recovery of subsurface properties in acousticmedia. In order to reduce the ill-posedness of the problem, the heterogeneous wave speed parameter is represented using a limited number of coefficients associated with a basis of eigenvectors of a diffusion equation, following theregularization by discretization approach. We compare several choices for the diffusion coefficient in the partial differential equations,which are extracted from the field of image processing. We first investigate their efficiency forimage decomposition (accuracy of the representation with respect to the number of variables). Next, we implement the method in the quantitative reconstruction procedure for seismic imaging, following the full waveform inversion method, where the difficulty resides in thatthe basis is defined from an initial model where none of the actual structures is known. In particular, we demonstrate that the method may be relevant for the reconstruction of media with salt-domes. We use the method in 2-D and 3-D experiments, and show that the eigenvector representation compensates for the lack of low-frequency information, it eventually serves usto extract guidelines for the implementation of the method. This work has been done with Florian Faucher (Faculty of Mathematics, Vienna) and Otmar Scherzer (University of Vienna). It has been published in 17.8.5.6 Bore reconstruction of woodwind instruments using the Full Waveform Inversion
Participants: Juliette Chabassier, Augustin Ernoult.
Several techniques can be used to reconstruct the internal geometry of a wind instrument from acoustics measurements. In this study, the passive linear acoustic response of the instrument is simulated and an optimization process is used to fit the simulation to the measurements. This technique can be seen as a first step toward the design of wind instruments, where the targeted acoustics properties come no more longer from measurements but are imposed by the designer. The difficulties of this approach are to find the best acoustic observation allowing the reconstruction (impedance, reflection function, etc.) but also to have an efficient optimization process. The "full waveform in-version" (FWI) is a technique coming from the seismology community. It uses the knowledge of the equation modeling the wave propagation into the instrument (here the telegraphist equation) to have an explicit expression of the gradient of the function which is minimized. This gradient is evaluated with a low computational cost. The FWI methodology, along with 1D spectral finite element discretization in space, applied to the woodwind instruments (with tone holes, losses and radiation) is presented in this communication. The results obtained for the bore reconstruction with different acoustics observations are then compared and discussed. This work has been presented at the conference Forum Acusticum 2020 21. subsubsectionAn effective numerical strategy for retrieving all characteristic parameters of an elastic scatterer from its FFP measurements.
Participants: Hélène Barucq, Julien Diaz.
A new computational strategy is proposed for determining all elastic scatterer characteristics including the shape, the material properties (Lamé coefficients and density), and the location from the knowledge of far-field pattern (FFP) measurements. The proposed numerical approach is a multi-stage procedure in which a carefully designed regularized iterative method plays a central role. The adopted approach is critical for recognizing that the different nature and scales of the sought-after parameters as well as the frequency regime have different effects on the scattering observability. Identification results for two-dimensional elastic configurations highlight the performance of the designed solution methodology. This is a joint work with Izar Aspiroz, research assistant at Vicomtech (Spain) and Rabia Djellouli, professor at CSUN (United States). It has been published in Journal of Computational Physics 7.
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
-
Depth Imaging Partnership (DIP3)
Period: 2019 May - 2021 December, Management: INRIA Bordeaux Sud-Ouest, Amount: 120000 euros/year.
-
Tent Pitcher algorithm for space-time integration of wave problems
Period: 2019 November - 2022 October, Management: INRIA Bordeaux Sud-Ouest, Amount: 165000 euros.
-
Isogeometric analysis of sharp boundaries in fullwaveform inversion
Period: 2019 January - 2021 December, Management: INRIA Bordeaux Sud-Ouest, Amount: 55000 euros.
-
FWI (Full Waveform Inversion) in the time domain based upon hybrid discontinuous numerical methods
Period: 2017 October - 2020 December , Management: INRIA Bordeaux Sud-Ouest, Amount: 180000 euros.
-
Petrophysics in pre-salt carbonate rocks
Period: 2019 November - 2021 June, Management: INRIA Bordeaux Sud-Ouest, Amount: 142000 euros.
10 Partnerships and cooperations
10.1 International initiatives
10.1.1 Inria associate team not involved in an IIL
ANTS
- Title: Advanced Numerical meThods for helioSeismology
- Duration: 2019 - 2022
- Coordinator: Ha Pham
- Partners: Max Plank Institut für Sonnensystemforschung (Germany) – Department Solar and Stellar Interiors – Laurent Gizon.
- Inria contact: Ha Howard Faucher
- Summary: Magique-3D proposes an Associate Team project, Advanced Numerical meThods for helioSeismology (ANTS), with the Max Planck Institute for Solar System Research (MPS), led by Laurent Gizon. The objective is to develop advanced software for accurate simulation of stellar oscillations and for the reconstruction of the Sun's interior. The novelty and challenge come from working with convected vector wave equations in the presence of complex flow and gravity, for a more accurate description of the physical phenomenon. The software will use Hybridizable Discontinuous Galerkin (HDG) approximation and will be developed on the existing platform Montjoie of Magique-3D. The scientific project benefits from the expertise of Magique-3D in seismic imaging, and the expert knowledge of the MPS group on Solar physics, in order to design accurate and efficient methodology. The project also helps strengthen the on-going collaboration between Magique-3D and MPS, that started two years ago. ANTS is indispensable to elevate the joint collaboration between Magique-3D and MPS. In addition, ANTS would extend the funds granted to Magique-3D on the theme, obtained from Université de Pau et des Pays de l'Adour through the E2S consortium, and which includes funding for PhD program and partial travel grants for the students. Finally, ANTS will be an essential propeller towards the submission of a project in the FETHPC-02-2019 campaign (where Magique-3D is the PI institution).
10.1.2 Inria international partners
Declared Inria international partners
The Berkeley Seismological Laboratory, University of California, Berkeley.
In September 2019, together with Barbara Romanowicz at the University of California Berkeley, https://
MAGIC2
- Title: Advance Modeling in Geophysics
- International Partner (Institution - Laboratory - Researcher):
- California State University at Northridge (United States) - Department of Mathematics - Djellouli Rabia
- The Associated Team MAGIC was created in January 2006 and renewed in January 2009. At the end of the program in December 2011, the two partners, Magique-3D and the California State University at Northridge (CSUN) decided to continue their collaboration and obtained the “Inria International Partner” label in 2013.
- See also: https://
project. inria. fr/ magic/ - The ultimate objective of this research collaboration is to develop efficient solution methodologies for solving inverse problems arising in various applications such as geophysical exploration, underwater acoustics, and electromagnetics. To this end, the research program will be based upon the following three pillars that are the key ingredients for successfully solving inverse obstacle problems. 1) The design of efficient methods for solving high-frequency wave problems. 2) The sensitivity analysis of the scattered field to the shape and parameters of heterogeneities/scatterers. 3) The construction of higher-order Absorbing Boundary Conditions.
10.2 International research visitors
10.2.1 Visits of international scientists
Mounir Tlemcani, from the University of Oran, spent two weeks in Pau in March 2020 .
10.3 European initiatives
10.3.1 FP7 & H2020 Projects
MATHROCKS
- Title: Multiscale Inversion of Porous Rock Physics using High-Performance Simulators: Bridging the Gap between Mathematics and Geophysics
- Duration: April 2018 - March 2022
- Coordinator: Universidad Del Pais Vasco (EHU UPV)
-
Partners:
- BARCELONA SUPERCOMPUTING CENTER - CENTRO NACIONAL DE SUPERCOMPUTACION (Spain)
- BCAM - BASQUE CENTER FOR APPLIED MATHEMATICS (Spain)
- CURTIN UNIVERSITY OF TECHNOLOGY (Australia)
- PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE (Chile)
- REPSOL SA (Spain)
- UNIVERSIDAD CENTRAL DE VENEZUELA (Venezuela)
- UNIVERSIDAD DE BUENOS AIRES (Argentina)
- UNIVERSIDAD DEL PAIS VASCO/ EUSKAL HERRIKO UNIBERTSITATEA (Spain)
- UNIVERSIDAD NACIONAL DE COLOMBIA (Colombia)
- UNIVERSITAT POLITECNICA DE CATALUNYA (Spain)
- Inria contact: Hélène BARUCQ
- Summary: We will develop and exchange knowledge on applied mathematics, high-performance computing (HPC), and geophysics to better characterize the Earth´s subsurface. We aim to better understand porous rocks physics in the context of elasto-acoustic wave propagation phenomena. We will develop parallel high-continuity isogeometric analysis (IGA) simulators for geophysics. We will design and implement fast and robust parallel solvers for linear equations to model multi-physics electromagnetic and elasto-acoustic phenomena. We seek to develop a parallel joint inversion workflow for electromagnetic and seismic geophysical measurements. To verify and validate these tools and methods, we will apply the results to: characterise hydrocarbon reservoirs, determine optimal locations for geothermal energy production, analyze earthquake propagation, and jointly invert deep-azimuthal resistivity and elasto-acoustic borehole measurements. Our target computer architectures for the simulation and inversion software infrastructure consists of distributed-memory parallel machines that incorporate the latest Intel Xeon Phi processors. Thus, we will build a hybrid OpenMP and MPI software framework. We will widely disseminate our collaborative research results through publications, workshops, postgraduate courses to train new researchers, a dedicated webpage with regular updates, and visits to companies working in the area. Therefore, we will perform a significant role in technology transfer between the most advanced numerical methods and mathematics, the latest super-computer architectures, and the area of applied geophysics.
10.3.2 Collaborations in European programs, except FP7 and H2020
PiXiL
- Title: Multiscale Inversion of Porous Rock Physics using High-Performance Simulators: Bridging the Gap between Mathematics and Geophysics
- Duration: September 2019 - April 2022
- Coordinator: BARCELONA SUPERCOMPUTING CENTER - CENTRO NACIONAL DE SUPERCOMPUTACION (Spain)
-
Partners:
- BARCELONA SUPERCOMPUTING CENTER - CENTRO NACIONAL DE SUPERCOMPUTACION (Spain)
- BCAM - BASQUE CENTER FOR APPLIED MATHEMATICS (Spain)
- UNIVERSIDAD DEL PAIS VASCO/ EUSKAL HERRIKO UNIBERTSITATEA (Spain)
- UNIVERSITAT de BARCELONA (Spain)
- REALTIMESEISMIC (RTS)
- PÔLE AVENIA
- Inria contact: Julien DIAZ
-
Summary:
Part of the FEDER Poctefa Program https://
www. poctefa. eu/, the PIXIL project is a transnational and multidisciplinary scientific and technological cooperation. Its main goal is to develop the most advanced tools to analyze the Earth's subsurface, with a special focus on fostering the uptake of geothermal energy in the region. The project will contribute to making the trans-Pyrenean area a technology hub in subsoil characterization within two years. Its success is expected to boost the wealth and creation of jobs related to the generation and management of underground natural resources in the area. -
See also:
https://
pixil-project. eu/ en
10.4 National initiatives
10.4.1 Depth Imaging Partnership
Magique-3D maintains active collaborations with Total. In the context of Depth Imaging, Magique-3D coordinates research activities dealing with the development of high-performance numerical methods for solving wave equations in complex media. This project has involved 2 other Inria Team-Projects (Hiepacs and Nachos) which have complementary skills in mathematics, computing and in geophysics. DIP is fully funded by Total by the way of an outline agreement with Inria .
The third phase of DIP began in 2019. Aurélien Citrain has been hired as engineer to work on the DIP platform. More than 10 PhD students have defended their PhD since the creation of DIP and most of them are now post-doctoral researchers or engineers in Europe. DIP is currently employing 3 PhD students.
10.5 Regional initiatives
10.5.1 Project supported by Conseil Régional d'Aquitaine
- title: Revival.
- Coordinator: Juliette Chabassier
- Other partners: Univ Bordeaux, Univ Montreal (Canada), Univ Cath. Louvain (Belgium)
The objective is to develop numerical tools for the virtual restoration of heritage instruments.
This project is supported by the Conseil Régional d'Aquitaine, for a duration of 2 years and has funded the postdoctoral position of Tobias van Baarsel since Feb 2019.
11 Dissemination
11.1 Promoting scientific activities
Reviewer - reviewing activities
Members of Magique 3D have been reviewers for the following journals:
- ESAIM: Mathematical Modelling and Numerical Analysis
- Geophysical Journal International
- International Journal on Geomathematics
- Journal Of Computational Physics
- International Journal for Numerical Methods in Engineering
- SIAM Journal on Scientific Computing
- SIAM Journal on Numerical Analysis
- SIAM journal on Applied Mathematics
- Inverse Problems
- Inverse Problems in Science & Engineering
- Journal of Acoustical Society of America
- Journal of Sound and Vibration
11.1.1 Leadership within the scientific community
- Augustin Ernoult is elected member of the "Groupe spécialisé d'acoustique musicale" (Gsam) of the french acoustical society.
- Hélène Barucq is elected member of the Liaison Committee of SMAI-GAMNI (Society of Applied and Industrial Mathematics - Group for promoting the Numerical Methods for Engineers).
11.1.2 Scientific expertise
- Since 2017, Hélène Barucq is chairwoman of a committee which evaluates research projects in Mathematics, Computer Science, Electronics and Optics to be funded by the Regional Council New Aquitaine
- Since 2018, Hélène Barucq is scientific officer for E2S project. She participates in the evaluation of each E2S call. She is also member of a committee having in charge the recruitment of non permanent researchers for E2S.
11.1.3 Research administration
- Julien Diaz is elected member of the Inria Technical Committee and of the Inria Administrative Board. He is appointed member of the Bureau du Comité des Projets (BCP) of Inria Bordeaux Sud-Ouest. Since 2018, he has been the head of the Mescal team of LMAP.
- Juliette Chabassier is member of the Research Position Commission of Inria Bordeaux Sud-Ouest.
- Juliette Chabassier is member of the Center Commitee of Inria Bordeaux Sud-Ouest.
- Rose-Cloé Meyer is elected member of Laboratory Commitee of LMAP.
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Licence : Rose-Cloé Meyer, Développements limités, suites et séries, 19.5h Eq. TD, L2, UPPA, France
- Master : Sébastien Tordeux, Outils Mathématiques pour la Mécanique, 49 eq. TD, Master1, UPPA, France
- Master : Margot Sirdey and Sébastien Tordeux, Introduction to wave phenomena, 48 eq. TD, Master, UPPA, France
- Licence : Sébastien Tordeux, Applied Mathematics, 18 eq. TD, L1, UPPA, France
11.2.2 Supervision
- Chengyi Shen, Approches expérimentale et numérique de la propagation d'ondes sismiques dans les roches carbonatées, June 3rd Julien Diaz and Daniel Brito (LFCR).
- PhD in progress : Alexandre Gras, Hybrid resonance for sensing applications, IOGS, October 2017, Philippe Lalanne(IOGS), Marc Duruflé, Hélène Barucq (Magique 3D).
- PhD in progress : Pierre Jacquet, Time domain Full Waveform Inversion involving hybrids numerical method to characterize elasto-acoustic media, October 2017, Hélène Barucq and Julien Diaz.
- PhD in progress: Victor Martins Gomez, Experimental characterization and modeling of seismo-electromagnetic waves, Université de Pau et des Pays de l'Adour, October 2018, Hélène Barucq and Daniel Brito (LFCR).
- PhD in progress : Rose-Cloé Meyer, Modeling of conducting poro-elastic media using advanced numerical methods , Université de Pau et des Pays de l'Adour, October 2018, Hélène Barucq, Julien Diaz and Ha Pham.
- PhD in progress : Nathan Rouxelin, Advanced numerical modeling of acoustic waves propagating below the surface of the Sun, Université de Pau et des Pays de l'Adour, October 2018, Hélène Barucq and Sébastien Tordeux.
- PhD in progress : Margot Sirdey, Méthode de Trefftz pour l'électromagnétisme, October 2019, Sébastien Tordeux and Sébastien Pernet (Onera).
- PhD in progress : Vinduja Vasanthan, Tent Pitcher algorithm for space-time integration of wave problems, October 2019, Hélène Barucq and Julien Diaz.
- PhD in progress : Stefano Frambati, Isogeometric analysis of sharp boundaries in full waveform inversion, January 2019, Hélène Barucq and Julien Diaz.
- PhD in progress : Alexis Thibault, Modeling and simulation of wind musical instruments, October 2020, Juliette Chabassier and Thomas Hélie (IRCAM).
- PhD in progress : Guillaume Castera, Modeling and simulation of the piano touch, October 2020, Juliette Chabassier and Paul Fisette (Louvain Cath. Univ., Belgium).
11.2.3 Juries
- Julien Diaz : Georges Nehmetallah (Université de Nice Côte d'Azur), Méthodes Galerkin discontinues hybrides couplées à des schémas de type explicite/implicite pour les équations de Maxwell instationnaires, PhD thesis, December 14th 2020, reviewer.
- Hélène Barucq : Pierre Payen (Université Paris 13 et CEA), Modélisation d’un empilement de matériaux dans le domaine fréquentiel par une condition d’impédance d’ordre élevé, December 16th 2020, Reviewer
- Hélène Barucq: Nourallah Dahmen (ISAE, Université Fédérale Toulouse Midi-Pyrénées), Développement d’un nouveau coeur numérique pour le code de calcul Salammbô de modélisation des ceintures de radiation terrestres, Reviewer.
- Juliette Chabassier : Erik Alan Petersen (Aix Marseille Université), Propagation d'ondes dans les milieux périodiques appliquée aux instruments à vent à trous latéraux. Comment s'équilibre la production et le rayonnement ?, Examiner.
11.3 Popularization
11.3.1 Articles and contents
Hélène Barucq contributed to an article in Binaire, a blog for the popularization of computer science. The article entitled "Le Soleil chante pour Hélène" is available at the following address https://
11.3.2 Interventions
- Augustin Ernoult participated to "Fête de la Science". He presented his research themes at "Lycée de Bazas" (Bazas high-school)
- Hélène Barucq participated to "Fête de la Science". She gave a talk entitled "Allo la Terre? Ici le Soleil" available online at https://
www. youtube. com/ watch?v=uySjljEwEOo
11.4 Creation of media or tools for science outreach
Juliette Chabassier co-created with the Ensemble Les Précieuses the show Louis 14.0 that presents how ancient instruments can be restored via numerical techniques, and played in real time in a musical and theatral show.
12 Scientific production
12.1 Major publications
- 1 article Sparsified discrete wave problem involving radiation condition on a prolate spheroidal surface IMA Journal of Numerical Analysis 2019
- 2 articleEfficient and Accurate Algorithm for the Full Modal Green's Kernel of the Scalar Wave Equation in HelioseismologySIAM Journal on Applied Mathematics806December 2020, 2657-2683
- 3 articleHybridizable discontinuous Galerkin method for the two-dimensional frequency-domain elastic wave equationsGeophysical Journal International2131April 2018, 637--659
- 4 articleWoodwind instrument design optimization based on impedance characteristics with geometric constraintsJournal of the Acoustical Society of America1485November 2020, 2864-2877
- 5 articleNonuniqueness of the quasinormal mode expansion of electromagnetic Lorentz dispersive materialsJournal of the Optical Society of America. A Optics, Image Science, and Vision3772020, 1219
- 6 articleA comparison of a one-dimensional finite element method and the transfer matrix method for the computation of wind music instrument impedanceActa Acustica united with Acustica10552019, 838
12.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Reports & preprints
12.3 Cited publications
- 34 book Asteroseismology Springer Science & Business Media 2010
- 35 article Probing the interior physics of stars through asteroseismology arXiv preprint arXiv:1912.12300 2019
- 36 articleInverse problem for the Helmholtz equation with Cauchy data: reconstruction with conditional well-posedness driven iterative regularizationESAIM: Mathematical Modelling and Numerical Analysis533May 2019, 1005-1030
- 37 articleThe mechanism producing initial transients on the clarinetThe Journal of the Acoustical Society of America14262017, 3376-3386
- 38 articleQuasistatic nonlinear characteristics of double-reed instrumentsThe Journal of the Acoustical Society of America12112007, 536-546
- 39 articleAbout the stability of the inverse problem in 1-D wave equations—Application to the interpretation of seismic profilesApplied Mathematics and Optimization511979, 1--47
- 40 articleSpace-time Trefftz-DG approximation for elasto-acousticsApplicable Analysis00August 2018, 1 - 16
- 41 articleStability analysis of heterogeneous Helmholtz problems and finite element solution based on propagation media approximationMathematics of Computation863072017, 2129 - 2157
- 42 articleGlobal seismology of the SunLiving Reviews in Solar Physics1312016, 2
- 43 articleDirect Simulation of Reed Wind InstrumentsComputer Music Journal3342009, 43-55
- 44 articleHybridizable discontinuous Galerkin method for the two-dimensional frequency-domain elastic wave equationsGeophysical Journal International2131April 2018, 637--659
- 45 articleInterpretation of helioseismic travel timesSpace Science Reviews1961-42015, 201--219
- 46 inproceedingsIdentification of functional parameters in partial differential equationsJoint Automatic Control Conference121974, 155--156
- 47 articleHelioseismologyReviews of Modern Physics7442002, 1073
- 48 articleImproved precision in measurements of acoustic impedance spectra using resonance-free calibration loads and controlled error distributionThe Journal of the Acoustical Society of America12132007, 1471-1481
- 49 phdthesis Contributions to Seismic Full Waveform Inversion for Time Harmonic Wave Equations: Stability Estimates, Convergence Analysis, Numerical Experiments involving Large Scale Optimization Algorithms Université de Pau et des Pays de l'Adour November 2017
- 50 articleSensitivity kernels for time-distance helioseismology-Efficient computation for spherically symmetric solar modelsAstronomy & Astrophysics6162018, A156
- 51 articleAcoustical impedance measurements by the two‐microphone‐three‐calibration (TMTC) methodThe Journal of the Acoustical Society of America8861990, 2533-2545
- 52 articleComputational helioseismology in the frequency domain: acoustic waves in axisymmetric solar models with flowsAstronomy and Astrophysics - A&A600April 2017, A35
- 53 articleLocal helioseismologyLiving Reviews in Solar Physics212005, 6
- 54 articleLocal helioseismology: three-dimensional imaging of the solar interiorAnnual Review of Astronomy and Astrophysics482010, 289--338
- 55 articleSignal and noise in helioseismic holographyAstronomy & Astrophysics6202018, A136
- 56 articleReal-time synthesis of clarinet-like instruments using digital impedance modelsThe Journal of the Acoustical Society of America11812005, 483-494
- 57 articleThe dispersion of surface waves on multilayered mediaBulletin of the seismological Society of America4311953, 17--34
- 58 articleGiant star seismologyThe Astronomy and Astrophysics Review2512017, 1
- 59 inproceedings Seismic imaging of supercritical geothermal reservoir using full-waveform inversion method Proceedings 2019
- 60 book Seismic wave propagation in stratified media ANU Press 2009
- 61 article3-D seismic exploration across the deep geothermal research platform GroßSchönebeck north of Berlin/GermanyGeothermal Energy712019, 1--18
- 62 inproceedingsThe seismic inverse problem as a sequence of before stack migrationsConference on inverse scattering: theory and applicationSiam Philadelphia, PA1983, 206--220
- 63 phdthesis Inversion of surface waves in an oil and gas exploration context Université Grenoble Alpes (ComUE) 2016
- 64 articleA review of the adjoint-state method for computing the gradient of a functional with geophysical applicationsGeophysical Journal International16722006, 495--503
- 65 articleGauss--Newton and full Newton methods in frequency--space seismic waveform inversionGeophysical Journal International13321998, 341--362
- 66 articleTwo-dimensional velocity models from wide-angle seismic data by wavefield inversionGeophysical Journal International12421996, 323--340
- 67 articleINVERSE THEORY APPLIED TO MULTI-SOURCE CROSS-HOLE TOMOGRAPHY. PART 1: ACOUSTIC WAVE-EQUATION METHOD 1Geophysical prospecting3831990, 287--310
- 68 articleSeismic attenuation due to wave-induced flowJ. Geophys. Res.1092004, 681-693
- 69 articleWebster's Horn Equation RevisitedSIAM Journal on Applied Mathematics6562005, 1981-2004
- 70 phdthesis Two-dimensional near-surface seismic imaging with surface waves: alternative methodology for waveform inversion 2013
- 71 articleProperty modelling of a potential CO2 storage site using seismic inversionEGUGA2013, EGU2013--10470
- 72 book Surface wave methods: acquisition, processing and inversion 2003
- 73 book Inverse problem theory and methods for model parameter estimation 89 siam 2005
- 74 book Inverse problem theory: methods for data fitting and model parameter estimation Amsterdam, Netherlands Elsevier Science Publishers 1987
- 75 articleTransmission of elastic waves through a stratified solid mediumJournal of applied Physics2121950, 89--93
- 76 articleDemonstrating storage of CO2 in geological reservoirs: The Sleipner and SACS projectsEnergy299-102004, 1361--1369
- 77 articleA comparison of a one-dimensional finite element method and the transfer matrix method for the computation of wind music instrument impedanceActa Acustica united with Acustica52019, 838
- 78 articleSound production in recorderlike instruments. II. A simulation modelThe Journal of the Acoustical Society of America10151997, 2925-2939
- 79 articleInfluence of fluid displacement patterns on seismic velocity during supercritical CO2 injection: Simulation study for evaluation of the relationship between seismic velocity and CO2 saturationInternational Journal of Greenhouse Gas Control462016, 197--204
- 80 phdthesis Modeling experiments in helioseismic holography Niedersächsische Staats-und Universitätsbibliothek Göttingen 2019

