Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.4. Multiscale modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.2. Numerical probability
- A6.2.3. Probabilistic methods
- A6.3. Computation-data interaction
- A6.3.4. Model reduction
Other Research Topics and Application Domains
- B1. Life sciences
- B1.2. Neuroscience and cognitive science
- B1.2.1. Understanding and simulation of the brain and the nervous system
- B1.2.2. Cognitive science
1 Team members, visitors, external collaborators
Research Scientists
- Mathieu Desroches [Team leader, Inria, Researcher, HDR]
- Fabien Campillo [Inria, Senior Researcher, HDR]
- Pascal Chossat [CNRS, Emeritus, HDR]
- Olivier Faugeras [Inria, Emeritus, HDR]
- Maciej Krupa [Univ Côte d'Azur, Senior Researcher, HDR]
- Simona Olmi [Inria, Starting Research Position]
- Romain Veltz [Inria, Researcher]
Post-Doctoral Fellow
- Emre Baspinar [Inria, until Nov 2020]
PhD Students
- Louisiane Lemaire [Inria]
- Yuri Rodrigues [Univ Côte d'Azur]
- Halgurd Taher [Inria]
Technical Staff
- Emre Baspinar [Inria, Engineer, from Dec 2020]
Interns and Apprentices
- Guillaume Girier [Inria, from Mar 2020 until Jun 2020]
- Mostafa Oukati Sadegh [Univ Côte d'Azur, from Mar 2020 until Apr 2020]
Administrative Assistant
- Marie-Cecile Lafont [Inria]
External Collaborators
- Daniele Avitabile [Université libre d'Amsterdam - Pays-Bas, HDR]
- Benjamin Aymard [Thales, until Feb 2020]
- Elif Köksal Ersöz [Univ de Rennes I]
2 Overall objectives
MathNeuro focuses on the applications of multi-scale dynamics to neuroscience. This involves the modelling and analysis of systems with multiple time scales and space scales, as well as stochastic effects. We look both at single-cell models, microcircuits and large networks. In terms of neuroscience, we are mainly interested in questions related to synaptic plasticity and neuronal excitability, in particular in the context of pathological states such as epileptic seizures and neurodegenerative diseases such as Alzheimer.
Our work is quite mathematical but we make heavy use of computers for numerical experiments and simulations. We have close ties with several top groups in biological neuroscience. We are pursuing the idea that the "unreasonable effectiveness of mathematics" can be brought, as it has been in physics, to bear on neuroscience.
Modeling such assemblies of neurons and simulating their behavior involves putting together a mixture of the most recent results in neurophysiology with such advanced mathematical methods as dynamical systems theory, bifurcation theory, probability theory, stochastic calculus, theoretical physics and statistics, as well as the use of simulation tools.
We conduct research in the following main areas:
- Neural networks dynamics
- Mean-field and stochastic approaches
- Neural fields
- Slow-fast dynamics in neuronal models
- Modeling neuronal excitability
- Synaptic plasticity
- Memory processes
- Visual neuroscience
3 Research program
3.1 Neural networks dynamics
The study of neural networks is certainly motivated by the long term goal to understand how brain is working. But, beyond the comprehension of brain or even of simpler neural systems in less evolved animals, there is also the desire to exhibit general mechanisms or principles at work in the nervous system. One possible strategy is to propose mathematical models of neural activity, at different space and time scales, depending on the type of phenomena under consideration. However, beyond the mere proposal of new models, which can rapidly result in a plethora, there is also a need to understand some fundamental keys ruling the behaviour of neural networks, and, from this, to extract new ideas that can be tested in real experiments. Therefore, there is a need to make a thorough analysis of these models. An efficient approach, developed in our team, consists of analysing neural networks as dynamical systems. This allows to address several issues. A first, natural issue is to ask about the (generic) dynamics exhibited by the system when control parameters vary. This naturally leads to analyse the bifurcations 71 72 occurring in the network and which phenomenological parameters control these bifurcations. Another issue concerns the interplay between the neuron dynamics and the synaptic network structure.
3.2 Mean-field and stochastic approaches
Modeling neural activity at scales integrating the effect of thousands of neurons is of central importance for several reasons. First, most imaging techniques are not able to measure individual neuron activity (microscopic scale), but are instead measuring mesoscopic effects resulting from the activity of several hundreds to several hundreds of thousands of neurons. Second, anatomical data recorded in the cortex reveal the existence of structures, such as the cortical columns, with a diameter of about 50 to 1, containing of the order of one hundred to one hundred thousand neurons belonging to a few different species. The description of this collective dynamics requires models which are different from individual neurons models. In particular, when the number of neurons is large enough averaging effects appear, and the collective dynamics is well described by an effective mean-field, summarizing the effect of the interactions of a neuron with the other neurons, and depending on a few effective control parameters. This vision, inherited from statistical physics requires that the space scale be large enough to include a large number of microscopic components (here neurons) and small enough so that the region considered is homogeneous.
Our group is developing mathematical and numerical methods allowing on one hand to produce dynamic mean-field equations from the physiological characteristics of neural structure (neurons type, synapse type and anatomical connectivity between neurons populations), and on the other so simulate these equations; see Figure 1. These methods use tools from advanced probability theory such as the theory of Large Deviations 60 and the study of interacting diffusions 3.
![Simulations of the quasi-synchronous state of a stochastic neural network with N=5000N=5000 neurons. Left: empirical distribution of membrane potential as a function (t,v)(t, v). Middle: (raster plot) spiking times as a function of neuron index and time. Right: several membrane potentials vi(t)v_i(t) as a function of time for i∈[1,100]i\in [1,100]. Simulated with the Julia Package PDMP.jl from . This figure has been slightly modified from .](/rapportsactivite/RA2020/mathneuro/WEB_IMG/adrv.png)
3.3 Neural fields
Neural fields are a phenomenological way of describing the activity of population of neurons by delayed integro-differential equations. This continuous approximation turns out to be very useful to model large brain areas such as those involved in visual perception. The mathematical properties of these equations and their solutions are still imperfectly known, in particular in the presence of delays, different time scales and noise.
Our group is developing mathematical and numerical methods for analysing these equations. These methods are based upon techniques from mathematical functional analysis, bifurcation theory 18, 74, equivariant bifurcation analysis, delay equations, and stochastic partial differential equations. We have been able to characterize the solutions of these neural fields equations and their bifurcations, apply and expand the theory to account for such perceptual phenomena as edge, texture 53, and motion perception. We have also developed a theory of the delayed neural fields equations, in particular in the case of constant delays and propagation delays that must be taken into account when attempting to model large size cortical areas 19, 73. This theory is based on center manifold and normal forms ideas 17.
3.4 Slow-fast dynamics in neuronal models
Neuronal rhythms typically display many different timescales, therefore it is important to incorporate this slow-fast aspect in models. We are interested in this modeling paradigm where slow-fast point models, using Ordinary Differential Equations (ODEs), are investigated in terms of their bifurcation structure and the patterns of oscillatory solutions that they can produce. To insight into the dynamics of such systems, we use a mix of theoretical techniques — such as geometric desingularisation and centre manifold reduction 64 — and numerical methods such as pseudo-arclength continuation 57. We are interested in families of complex oscillations generated by both mathematical and biophysical models of neurons. In particular, so-called mixed-mode oscillations (MMOs)11, 55, 63, which represent an alternation between subthreshold and spiking behaviour, and bursting oscillations56, 62, also corresponding to experimentally observed behaviour 54; see Figure 2. We are working on extending these results to spatio-temporal neural models 2.
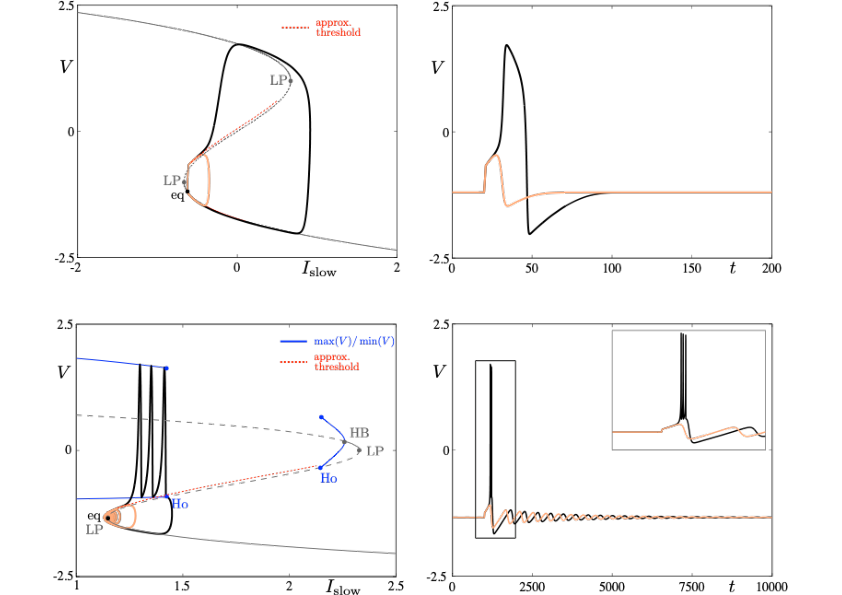
3.5 Modeling neuronal excitability
Excitability refers to the all-or-none property of neurons 59, 61. That is, the ability to respond nonlinearly to an input with a dramatic change of response from “none” — no response except a small perturbation that returns to equilibrium — to “all” — large response with the generation of an action potential or spike before the neuron returns to equilibrium. The return to equilibrium may also be an oscillatory motion of small amplitude; in this case, one speaks of resonator neurons as opposed to integrator neurons. The combination of a spike followed by subthreshold oscillations is then often referred to as mixed-mode oscillations (MMOs) 55. Slow-fast ODE models of dimension at least three are well capable of reproducing such complex neural oscillations. Part of our research expertise is to analyse the possible transitions between different complex oscillatory patterns of this sort upon input change and, in mathematical terms, this corresponds to understanding the bifurcation structure of the model. Furthermore, the shape of time series of this sort with a given oscillatory pattern can be analysed within the mathematical framework of dynamic bifurcations; see the section on slow-fast dynamics in Neuronal Models. The main example of abnormal neuronal excitability is hyperexcitability and it is important to understand the biological factors which lead to such excess of excitability and to identify (both in detailed biophysical models and reduced phenomenological ones) the mathematical structures leading to these anomalies. Hyperexcitability is one important trigger for pathological brain states related to various diseases such as chronic migraine 66, epilepsy 75 or even Alzheimer's Disease 65. A central central axis of research within our group is to revisit models of such pathological scenarios, in relation with a combination of advanced mathematical tools and in partnership with biological labs.
3.6 Synaptic Plasticity
Neural networks show amazing abilities to evolve and adapt, and to store and process information. These capabilities are mainly conditioned by plasticity mechanisms, and especially synaptic plasticity, inducing a mutual coupling between network structure and neuron dynamics. Synaptic plasticity occurs at many levels of organization and time scales in the nervous system 52. It is of course involved in memory and learning mechanisms, but it also alters excitability of brain areas and regulates behavioral states (e.g., transition between sleep and wakeful activity). Therefore, understanding the effects of synaptic plasticity on neurons dynamics is a crucial challenge.
Our group is developing mathematical and numerical methods to analyse this mutual interaction. On the one hand, we have shown that plasticity mechanisms 9, 15, Hebbian-like or STDP, have strong effects on neuron dynamics complexity, such as synaptic and propagation delays 19, dynamics complexity reduction, and spike statistics.
3.7 Memory processes
The processes by which memories are formed and stored in the brain are multiple and not yet fully understood. What is hypothesised so far is that memory formation is related to the activation of certain groups of neurons in the brain. Then, one important mechanism to store various memories is to associate certain groups of memory items with one another, which then corresponds to the joint activation of certain neurons within different subgroup of a given population. In this framework, plasticity is key to encode the storage of chains of memory items. Yet, there is no general mathematical framework to model the mechanism(s) behind these associative memory processes. We are aiming at developing such a framework using our expertise in multi-scale modelling, by combining the concepts of heteroclinic dynamics, slow-fast dynamics and stochastic dynamics.
The general objective that we wish to purse in this project is to investigate non-equilibrium phenomena pertinent to memory storage and retrieval. Earlier work, including the paper by team members 1, has shown that heteroclinic cycles can play an organizing role in the dynamics of firing rate models. Our goal is to explore other formulations to show the correspondence between the firing rate and other modeling contexts.
4 Application domains
The project underlying MathNeuro revolves around pillars of neuronal behaviour –excitability, plasticity, memory– in link with the initiation and propagation of pathological brain states in diseases such as cortical spreading depression (in link with certain forms of migraine with aura), epileptic seizures and Alzheimer’s Disease.
5 New results
5.1 Neural Networks as dynamical systems
5.1.1 A mean-field approach to the dynamics of networks of complex neurons, from nonlinear Integrate-and-Fire to Hodgkin-Huxley models
Participants: Mallory Carlu, Omar Chehab, Leonardo Dalla Porta, Damien Depannemaecker, Charlotte Héricé, Maciej Jedynak, Elif Köksal Ersöz, Paolo Muratore, Selma Souihel, Cristiano Capone , Yan Zerlaut, Alain Destexhe, Matteo Di Volo.
We present a mean-field formalism able to predict the collective dynamics of large networks of conductance-based interacting spiking neurons. We apply this formalism to several neuronal models, from the simplest Adaptive Exponential Integrate-and-Fire model to the more complex Hodgkin-Huxley and Morris-Lecar models. We show that the resulting mean-field models are capable of predicting the correct spontaneous activity of both excitatory and inhibitory neurons in asynchronous irregular regimes, typical of cortical dynamics. Moreover, it is possible to quantitatively predict the populations response to external stimuli in the form of external spike trains. This mean-field formalism therefore provides a paradigm to bridge the scale between population dynamics and the microscopic complexity of the individual cells physiology.This work has been published in Journal of Neurophysiology and is available as 24.
5.1.2 Theta-Nested Gamma Oscillations in Next Generation Neural Mass Models
Participants: Marco Segneri, Hongjie Bi, Simona Olmi, Alessandro Torcini.
Theta-nested gamma oscillations have been reported in many areas of the brain and are believed to represent a fundamental mechanism to transfer information across spatial and temporal scales. In a series of recent experiments in vitro it has been possible to replicate with an optogenetic theta frequency stimulation several features of cross-frequency coupling (CFC) among theta and gamma rhythms observed in behaving animals. In order to reproduce the main findings of these experiments we have considered a new class of neural mass models able to reproduce exactly the macroscopic dynamics of spiking neural networks. In this framework, we have examined two set-ups able to support collective gamma oscillations: namely, the pyramidal interneuronal network gamma (PING) and the interneuronal network gamma (ING). In both set-ups we observe the emergence of theta-nested gamma oscillations by driving the system with a sinusoidal theta-forcing in proximity of a Hopf bifurcation. These mixed rhythms always display phase amplitude coupling. However, two different types of nested oscillations can be identified: one characterized by a perfect phase locking between theta and gamma rhythms, corresponding to an overall periodic behavior; another one where the locking is imperfect and the dynamics is quasi-periodic or even chaotic. From our analysis it emerges that the locked states are more frequent in the ING set-up. In agreement with the experiments, we find theta-nested gamma oscillations for forcing frequencies in the range [1:10] Hz, whose amplitudes grow proportionally to the forcing intensity and which are clearly modulated by the theta phase. Furthermore, analogously to the experiments, the gamma power and the frequency of the gamma-power peak increase with the forcing amplitude. At variance with experimental findings, the gamma-power peak does not shift to higher frequencies by increasing the theta frequency. This effect can be obtained, in our model, only by incrementing, at the same time, also the stimulation power. An effect achieved by increasing the amplitude either of the noise or of the forcing term proportionally to the theta frequency. On the basis of our analysis both the PING and the ING mechanism give rise to theta-nested gamma oscillations with almost identical features.This work has been published in Frontiers in Computational Neuroscience and is available as 35.
5.1.3 Exact neural mass model for synaptic-based working memory
Participants: Halgurd Taher, Alessandro Torcini, Simona Olmi.
A synaptic theory of Working Memory (WM) has been developed in the last decade as a possible alternative to the persistent spiking paradigm. In this context, we have developed a neural mass model able to reproduce exactly the dynamics of heterogeneous spiking neural networks encompassing realistic cellular mechanisms for short-term synaptic plasticity. This population model reproduces the macroscopic dynamics of the network in terms of the firing rate and the mean membrane potential. The latter quantity allows us to gain insight of the Local Field Potential and electroencephalographic signals measured during WM tasks to characterize the brain activity. More specifically synaptic facilitation and depression integrate each other to efficiently mimic WM operations via either synaptic reactivation or persistent activity. Memory access and loading are related to stimulus-locked transient oscillations followed by a steady-state activity in the band, thus resembling what is observed in the cortex during vibrotactile stimuli in humans and object recognition in monkeys. Memory juggling and competition emerge already by loading only two items. However more items can be stored in WM by considering neural architectures composed of multiple excitatory populations and a common inhibitory pool. Memory capacity depends strongly on the presentation rate of the items and it maximizes for an optimal frequency range. In particular we provide an analytic expression for the maximal memory capacity. Furthermore, the mean membrane potential turns out to be a suitable proxy to measure the memory load, analogously to event driven potentials in experiments on humans. Finally we show that the *γ* power increases with the number of loaded items, as reported in many experiments, while and power reveal non monotonic behaviours. In particular, and rhythms are crucially sustained by the inhibitory activity, while the rhythm is controlled by excitatory synapses.This work has been published in PLoS Computational Biology and is available as 36.
5.1.4 Control of synchronization in two-layer power grids
Participants: Carl Totz, Simona Olmi, Eckehard Schöll.
In this work we suggest modeling the dynamics of power grids in terms of a two-layer network, and we use the Italian high-voltage power grid as a proof-of-principle example. The first layer in our model represents the power grid consisting of generators and consumers, while the second layer represents a dynamic communication network that serves as a controller of the first layer. In particular, the dynamics of the power grid is modeled by the Kuramoto model with inertia, while the communication layer provides a control signal for each generator to improve frequency synchronization within the power grid. We propose different realizations of the communication layer topology and different ways to calculate the control signal. Then we conduct a systematic survey of the two-layer system against a multitude of different realistic perturbation scenarios, such as disconnecting generators, increasing demand of consumers, or generators with stochastic power output. When using a control topology that allows all generators to exchange information, we find that a control scheme aimed to minimize the frequency difference between adjacent nodes operates very efficiently even against the worst scenarios with the strongest perturbations.This work has been published in Physical Review E and is available as 37.
5.1.5 Modeling dopaminergic modulation of clustered gamma rhythms
Participants: Denis Zakharov, Martin Krupa, Boris Gutkin.
Gamma rhythm (20-100Hz) plays a key role in numerous cognitive tasks: working memory, sensory processing and in routing of information across neural circuits. In comparison with lower frequency oscillations in the brain, gamma-rhythm associated firing of the individual neurons is sparse and the activity is locally distributed in the cortex. Such “weak” gamma rhythm results from synchronous firing of pyramidal neurons in an interplay with the local inhibitory interneurons in a “pyramidal-interneuron gamma” or PING. Experimental evidence shows that individual pyramidal neurons during such oscillations tend to fire at rates below gamma, with the population showing clear gamma oscillations and synchrony. One possible way to describe such features is that this gamma oscillation is generated within local synchronous neuronal clusters. The number of such synchronous clusters defines the overall coherence of the rhythm and its spatial structure. The number of clusters in turn depends on the properties of the synaptic coupling and the intrinsic properties of the constituent neurons. We previously showed that a slow spike frequency adaptation current in the pyramidal neurons can effectively control cluster numbers. These slow adaptation currents are modulated by endogenous brain neuromodulators such as dopamine, whose level is in turn related to cognitive task requirements. Hence we postulate that dopaminergic modulation can effectively control the clustering of weak gamma and its coherence. In this paper we study how dopaminergic modulation of the network and cell properties impacts the cluster formation process in a PING network model.This work has been published in Communications in Nonlinear Science and Numerical Simulation and is available as 38.
5.2 Mean field theory and stochastic processes
5.2.1 Coherence resonance in neuronal populations: mean-field versus network model
Participants: Emre Baspinar, Leonard Schülen, Simona Olmi, Anna Zakharova.
The counter-intuitive phenomenon of coherence resonance describes a non-monotonic behavior of the regularity of noise-induced oscillations in the excitable regime, leading to an optimal response in terms of regularity of the excited oscillations for an intermediate noise intensity. We study this phenomenon in populations of FitzHugh-Nagumo (FHN) neurons with different coupling architectures. For networks of FHN systems in excitable regime, coherence resonance has been previously analyzed numerically. Here we focus on an analytical approach studying the mean-field limits of the locally and globally coupled populations. The mean-field limit refers to the averaged behavior of a complex network as the number of elements goes to infinity. We derive a mean-field limit approximating the locally coupled FHN network with low noise intensities. Further, we apply mean-field approach to the globally coupled FHN network. We compare the results of the mean-field and network frameworks for coherence resonance and find a good agreement in the globally coupled case, where the correspondence between the two approaches is sufficiently good to capture the emergence of anticoherence resonance. Finally, we study the effects of the coupling strength and noise intensity on coherence resonance for both the network and the mean-field model.This work has been submitted for publications and is available as 42.
5.2.2 Cross frequency coupling in next generation inhibitory neural mass models
Participants: Andrea Ceni, Simona Olmi, Alessandro Torcini, David Angulo-Garcia.
Coupling among neural rhythms is one of the most important mechanisms at the basis of cognitive processes in the brain. In this study, we consider a neural mass model, rigorously obtained from the microscopic dynamics of an inhibitory spiking network with exponential synapses, able to autonomously generate collective oscillations (COs). These oscillations emerge via a super-critical Hopf bifurcation, and their frequencies are controlled by the synaptic time scale, the synaptic coupling, and the excitability of the neural population. Furthermore, we show that two inhibitory populations in a master–slave configuration with different synaptic time scales can display various collective dynamical regimes: damped oscillations toward a stable focus, periodic and quasi-periodic oscillations, and chaos. Finally, when bidirectionally coupled, the two inhibitory populations can exhibit different types of cross-frequency couplings (CFCs): phase-phase and phase-amplitude CFC. The coupling between and COs is enhanced in the presence of an external forcing, reminiscent of the type of modulation induced in hippocampal and cortex circuits via optogenetic drive.This work has been published in Chaos and is available as 25.
5.2.3 Emergent excitability in populations of nonexcitable units
Participants: Marzena Ciszak, Francesco Marino, Alessandro Torcini, Simona Olmi.
Population bursts in a large ensemble of coupled elements result from the interplay between the local excitable properties of the nodes and the global network topology. Here, collective excitability and self-sustained bursting oscillations are shown to spontaneously emerge in globally coupled populations of nonexcitable units subject to adaptive coupling. The ingredients to observe collective excitability are the coexistence of states with different degrees of synchronization joined to a global feedback acting, on a slow timescale, against the synchronization (desynchronization) of the oscillators. These regimes are illustrated for two paradigmatic classes of coupled rotators, namely, the Kuramoto model with and without inertia. For the bimodal Kuramoto model we analytically show that the macroscopic evolution originates from the existence of a critical manifold organizing the fast collective dynamics on a slow timescale. Our results provide evidence that adaptation can induce excitability by maintaining a network permanently out of equilibrium.This work has been published in Physical Review E and is available as 27.
5.2.4 Long time behavior of a mean-field model of interacting neurons
Participants: Quentin Cormier, Étienne Tanré, Romain Veltz.
We study the long time behavior of the solution to some McKean-Vlasov stochastic differential equation (SDE) driven by a Poisson process. In neuroscience, this SDE models the asymptotic dynamics of the membrane potential of a spiking neuron in a large network. We prove that for a small enough interaction parameter, any solution converges to the unique (in this case) invariant measure. To this aim, we first obtain global bounds on the jump rate and derive a Volterra type integral equation satisfied by this rate. We then replace temporary the interaction part of the equation by a deterministic external quantity (we call it the external current). For constant current, we obtain the convergence to the invariant measure. Using a perturbation method, we extend this result to more general external currents. Finally, we prove the result for the non-linear McKean-Vlasov equation.This work has been published in Stochastic Processes and their Applications and is available as 28.
5.2.5 Hopf bifurcation in a Mean-Field model of spiking neurons
Participants: Quentin Cormier, Etienne Tanré, Romain Veltz.
We study a family of non-linear McKean-Vlasov SDEs driven by a Poisson measure, modelling the mean-field asymptotic of a network of generalized Integrate-and-Fire neurons. We give sufficient conditions to have periodic solutions through a Hopf bifurcation. Our spectral conditions involve the location of the roots of an explicit holomorphic function. The proof relies on two main ingredients. First, we introduce a discrete time Markov Chain modeling the phases of the successive spikes of a neuron. The invariant measure of this Markov Chain is related to the shape of the periodic solutions. Secondly, we use the Lyapunov-Schmidt method to obtain self-consistent oscillations. We illustrate the result with a toy model for which all the spectral conditions can be analytically checked.This work has been submitted for publications and is available as 44.
5.2.6 Canard resonance: on noise-induced ordering of trajectories in heterogeneous networks of slow-fast systems
Participants: Otti d'Huys, Romain Veltz, Axel Dolcemascolo, Francesco Marino, Stéphane Barland.
We analyze the dynamics of a network of semiconductor lasers coupled via their mean intensity through a nonlinear optoelectronic feedback loop. We establish experimentally the excitable character of a single node, which stems from the slow-fast nature of the system, adequately described by a set of rate equations with three well separated time scales. Beyond the excitable regime, the system undergoes relaxation oscillations where the nodes display canard dynamics. We show numerically that, without noise, the coupled system follows an intricate canard trajectory, with the nodes switching on one by one. While incorporating noise leads to a better correspondence between numerical simulations and experimental data, it also has an unexpected ordering effect on the canard orbit, causing the nodes to switch on closer together in time. We find that the dispersion of the trajectories of the network nodes in phase space is minimized for a non-zero noise strength, and call this phenomenon Canard Resonance.This work has been published in Journal of Physics Photonics and is available as 29.
5.2.7 Effective low-dimensional dynamics of a mean-field coupled network of slow-fast spiking lasers
Participants: Axel Dolcemascolo, Alexandre Miazek, Romain Veltz, Francesco Marino, Stéphane Barland.
Low dimensional dynamics of large networks is the focus of many theoretical works, but controlled laboratory experiments are comparatively very few. Here, we discuss experimental observations on a mean-field coupled network of hundreds of semiconductor lasers, which collectively display effectively low-dimensional mixed mode oscillations and chaotic spiking typical of slow-fast systems. We demonstrate that such a reduced dimensionality originates from the slow-fast nature of the system and of the existence of a critical manifold of the network where most of the dynamics takes place. Experimental measurement of the bifurcation parameter for different network sizes corroborate the theory.This work has been published in Physical Review E and is available as 30.
5.2.8 Asymptotic behaviour of a network of neurons with random linear interactions
Participants: Olivier Faugeras, Émilie Soret, Étienne Tanré.
We study the asymptotic behaviour for asymmetric neuronal dynamics in a network of linear Hopfield neurons. The randomness in the network is modelled by random couplings which are centered i.i.d. random variables with finite moments of all orders. We prove that if the initial condition of the network is a set of i.i.d random variables with finite moments of all orders and independent of the synaptic weights, each component of the limit system is described as the sum of the corresponding coordinate of the initial condition with a centered Gaussian process whose covariance function can be described in terms of a modified Bessel function. This process is not Markovian. The convergence is in law almost surely w.r.t. the random weights. Our method is essentially based on the CLT and the method of moments.This work has been submitted for publication and is available as 46.
5.2.9 On a toy network of neurons interacting through their dendrites
Participants: Nicolas Fournier, Etienne Tanré, Romain Veltz.
Consider a large number of neurons, each being connected to approximately other ones, chosen at random. When a neuron spikes, which occurs randomly at some rate depending on its electric potential, its potential is set to a minimum value vmin, and this initiates, after a small delay, two fronts on the (linear) dendrites of all the neurons to which it is connected. Fronts move at constant speed. When two fronts (on the dendrite of the same neuron) collide, they annihilate. When a front hits the soma of a neuron, its potential is increased by a small value . Between jumps, the potentials of the neurons are assumed to drift in , according to some well-posed ODE. We prove the existence and uniqueness of a heuristically derived mean-field limit of the system when with . We make use of some recent versions of the results of Deuschel and Zeitouni 58 concerning the size of the longest increasing subsequence of an i.i.d. collection of points in the plan. We also study, in a very particular case, a slightly different model where the neurons spike when their potential reach some maximum value , and find an explicit formula for the (heuristic) mean-field limit. This work has been accepted for publication in Annales de l'Institut Henri Poincaré (B) Probabilités et Statistiques and is available as 31.5.2.10 Bumps and oscillons in networks of spiking neurons
Participants: Helmut Schmidt, Daniele Avitabile.
We study localized patterns in an exact mean-field description of a spatially-extended network of quadratic integrate-and-fire (QIF) neurons. We investigate conditions for the existence and stability of localized solutions, so-called bumps, and give an analytic estimate for the parameter range where these solutions exist in parameter space, when one or more microscopic network parameters are varied. We develop Galerkin methods for the model equations, which enable numerical bifurcation analysis of stationary and time-periodic spatially-extended solutions. We study the emergence of patterns composed of multiple bumps, which are arranged in a snake-and-ladder bifurcation structure if a homogeneous or heterogeneous synaptic kernel is suitably chosen. Furthermore, we examine time-periodic, spatially-localized solutions (oscillons) in the presence of external forcing, and in autonomous, recurrently coupled excitatory and inhibitory networks. In both cases we observe period doubling cascades leading to chaotic oscillations.This work has been published in Chaos and is available as 34.
5.2.11 Enhancing power grid synchronization and stability through time delayed feedback control of solitary states
Participants: Halgurd Taher, Simona Olmi, Eckehard Schöll.
Effective upon acceptance for publication, copyright (including all rights hereunder and the right to obtain copyright registration in the name of the copyright owner), the above article is hereby transferred throughout the world and for the full term and all extensions and renewals thereof, to EUROPEAN CONTROL ASSOCIATION (EUCA) This transfer includes the right to adapt the article for use in conjunction with computer systems and programs, including reproduction or publication in machine-readable form and incorporation in retrieval systems. Some papers accepted for ECC are considered for subsequent publication in the European Journal of Control (EJC). If the signing author has not been informed in writing within three months of the closing date of the conference that the paper is being so considered, he and his co-authors are free to submit the paper elsewhere, provided that full acknowledgement is given in any subsequent publication to the original ECC Proceedings CD-ROM and to the conference. Note: All copies, paper or electronic, or other use of the information must include an indication of the EUCA copyright and a full citation of the ECC Proceedings source.This work has been published in the proceedings of the 2020 IEEE European Control Conference (ECC) and is available as 39.
5.2.12 Slow-fast dynamics in the mean-field limit of neural networks
Participants: Daniele Avitabile, Emre Baspinar, Mathieu Desroches, Olivier Faugeras.
In the context of the Human Brain Project (HBP, see section 5.1.1.1. below), we have recruited Emre Baspinar in December 2018 for a two-year postdoc. Within MathNeuro, Emre is working on analysing slow-fast dynamical behaviours in the mean-field limit of neural networks.In a first project, he has been analysing the slow-fast structure in the mean-field limit of a network of FitzHugh-Nagumo neuron models; the mean-field was previously established in 3 but its slow-fast aspect had not been analysed. In particular, he has proved a persistence result of Fenichel type for slow manifolds in this mean-field limit, thus extending previous work by Berglund et al. 51, 50. A manuscript is in preparation.
In a second project, he has been looking at a network of Wilson-Cowan systems whose mean-field limit is an ODE, and he has studied elliptic bursting dynamics in both the network and the limit: its slow-fast dissection, its singular limits and the role of canards. In passing, he has obtained a new characterisation of ellipting bursting via the construction of periodic limit sets using both the slow and the fast singular limits and unravelled a new singular-limit scenario giving rise to elliptic bursting via a new type of torus canard orbits. A manuscript has been submitted for publication 41 (see below).
5.3 Neural fields theory
5.3.1 The hyperbolic model for edge and texture detection in the primary visual cortex
Participants: Pascal Chossat.
The modelling of neural fields in the visual cortex involves geometrical structures which describe in mathematical formalism the functional architecture of this cortical area. The case of contour detection and orientation tuning has been extensively studied and has become a paradigm for the mathematical analysis of image processing by the brain. Ten years ago an attempt was made to extend these models by replacing orientation (an angle) with a second-order tensor built from the gradient of the image intensity and named the structure tensor. This assumption does not follow from biological observations (experimental evidence is still lacking) but from the idea that the effectiveness of texture processing with the stucture tensor in computer vision may well be exploited by the brain itself. The drawback is that in this case the geometry is not Euclidean but hyperbolic instead, which complicates substantially the analysis. The purpose of this review is to present the methodology that was developed in a series of papers to investigate this quite unusual problem, specifically from the point of view of tuning and pattern formation. These methods, which rely on bifurcation theory with symmetry in the hyperbolic context, might be of interest for the modelling of other features such as color vision, or other brain functions.This work has been published in Journal of Mathematical Neuroscience and is available as 26.
5.4 Slow-fast dynamics in Neuroscience
5.4.1 Inflection, Canards and Folded Singularities in Excitable Systems: Application to a 3D FitzHugh–Nagumo Model
Participants: Jone Uria Albizuri, Mathieu Desroches, Martin Krupa, Serafim Rodrigues.
Specific kinds of physical and biological systems exhibit complex Mixed-Mode Oscillations mediated by folded-singularity canards in the context of slow-fast models. The present manuscript revisits these systems, specifically by analysing the dynamics near a folded singularity from the viewpoint of inflection sets of the flow. Originally, the inflection set method was developed for planar systems [Brøns and Bar-Eli in Proc R Soc A 445(1924):305–322, 1994; Okuda in Prog Theor Phys 68(6):1827–1840, 1982; Peng et al. in Philos Trans R Soc A 337(1646):275–289, 1991] and then extended to -dimensional systems [Ginoux et al. in Int J Bifurc Chaos 18(11):3409–3430, 2008], although not tailored to specific dynamics (e.g. folded singularities). In our previous study, we identified components of the inflection sets that classify several canard-type behaviours in 2D systems [Desroches et al. in J Math Biol 67(4):989–1017, 2013]. Herein, we first survey the planar approach and show how to adapt it for 3D systems with an isolated folded singularity by considering a suitable reduction of such 3D systems to planar non-autonomous slow-fast systems. This leads us to the computation of parametrized families of inflection sets of one component of that planar (non-autonomous) system, in the vicinity of a folded node or of a folded saddle. We then show that a novel component of the inflection set emerges, which approximates and follows the axis of rotation of canards associated to folded-node and folded-saddle singularities. Finally, we show that a similar inflection-set component occurs in the vicinity of a delayed Hopf bifurcation, a scenario that can arise at the transition between folded node and folded saddle. These results are obtained in the context of a canonical model for folded-singularity canards and subsequently we show it is also applicable to complex slow-fast models. Specifically, we focus the application towards the self-coupled 3D FitzHugh–Nagumo model, but the method is generically applicable to higher-dimensional models with isolated folded singularities, for instance in conductance-based models and other physical-chemical systems.This work has been published in Journal of Nonlinear Science and is available as 20.
5.4.2 Local theory for spatio-temporal canards and delayed bifurcations
Participants: Daniele Avitabile, Mathieu Desroches, Romain Veltz, Martin Wechselberger.
We present a rigorous framework for the local analysis of canards and slow passages through bifurcations in a wide class of infinite-dimensional dynamical systems with time-scale separation. The framework is applicable to models where an infinite-dimensional dynamical system for the fast variables is coupled to a finite-dimensional dynamical system for slow variables. We prove the existence of centre-manifolds for generic models of this type, and study the reduced, finite-dimensional dynamics near bifurcations of (possibly) patterned steady states in the layer problem. Theoretical results are complemented with detailed examples and numerical simulations covering systems of local- and nonlocal-reaction diffusion equations, neural field models, and delay-differential equations. We provide analytical foundations for numerical observations recently reported in literature, such as spatio-temporal canards and slow-passages through Hopf bifurcations in spatially-extended systems subject to slow parameter variations. We also provide a theoretical analysis of slow passage through a Turing bifurcation in local and nonlocal models.This work has been published in SIAM Journal on Mathematical Analysis and is available as 21.
5.4.3 Pseudo-plateau bursting and mixed-mode oscillations in a model of developing inner hair cells
Participants: Harun Baldemir, Daniele Avitabile, Krasimira Tsaneva-Atanasova.
Inner hair cells (IHCs) are excitable sensory cells in the inner ear that encode acoustic information. Before the onset of hearing IHCs fire calcium-based action potentials that trigger transmitter release onto developing spiral ganglion neurones. There is accumulating experimental evidence that these spontaneous firing patterns are associated with maturation of the IHC synapses and hence involved in the development of hearing. The dynamics organising the IHCs' electrical activity are therefore of interest.Building on our previous modelling work we propose a three-dimensional, reduced IHC model and carry out non-dimensionalisation. We show that there is a significant range of parameter values for which the dynamics of the reduced (three-dimensional) model map well onto the dynamics observed in the original biophysical (four-dimensional) IHC model. By estimating the typical time scales of the variables in the reduced IHC model we demonstrate that this model could be characterised by two fast and one slow or one fast and two slow variables depending on biophysically relevant parameters that control the dynamics. Specifically, we investigate how changes in the conductance of the voltage-gated calcium channels as well as the parameter corresponding to the fraction of free cytosolic calcium concentration in the model affect the oscillatory model bahaviour leading to transition from pseudo-plateau bursting to mixed-mode oscillations. Hence, using fast-slow analysis we are able to further our understanding of this model and reveal a path in the parameter space connecting pseudo-plateau bursting and mixed-mode oscillations by varying a single parameter in the model.
This work has been published in Communications in Nonlinear Science and Numerical Simulation and is available as 22.
5.4.4 Canonical models for torus canards in elliptic burster
Participants: Emre Baspinar, Daniele Avitabile, Mathieu Desroches.
We revisit elliptic bursting dynamics from the viewpoint of torus canard solutions. We show that at the transition to and from elliptic burstings, classical or mixed-type torus canards can appear, the difference between the two being the fast subsystem bifurcation that they approach, saddle-node of cycles for the former and subcritical Hopf for the latter. We first showcase such dynamics in a Wilson-Cowan type elliptic bursting model, then we consider minimal models for elliptic bursters in view of finding transitions to and from bursting solutions via both kinds of torus canards. We first consider the canonical model proposed by Izhikevich (ref. [22] in the manuscript) and adapted to elliptic bursting by Ju, Neiman, Shilnikov (ref. [24] in the manuscript), and we show that it does not produce mixed-type torus canards due to a nongeneric transition at one end of the bursting regime. We therefore introduce a perturbative term in the slow equation, which extends this canonical form to a new one that we call Leidenator and which supports the right transitions to and from elliptic bursting via classical and mixed-type torus canards, respectively. Throughout the study, we use singular flows () to predict the full system's dynamics ( small enough). We consider three singular flows: slow, fast and average slow, so as to appropriately construct singular orbits corresponding to all relevant dynamics pertaining to elliptic bursting and torus canards.This work has been submitted for publication and is available as 41.
5.4.5 Canard-induced complex oscillations in an excitatory network
Participants: Elif Köksal Ersöz, Mathieu Desroches, Antoni Guillamon, John Rinzel, Joel Tabak.
In this work we have revisited a rate model that accounts for the spontaneous activity in the developing spinal cord of the chicken embryo 70. The dynamics is that of a classical square-wave burster, with alternation of silent and active phases. Tabak et al. 70 have proposed two different three-dimensional (3D) models with variables representing average population activity, fast activity-dependent synaptic depression and slow activity-dependent depression of two forms. In 67, 68, 69 various 3D combinations of these four variables have been studied further to reproduce rough experimental observations of spontaneous rhythmic activity. In this work, we have first shown the spike-adding mechanism via canards in one of these 3D models from 70 where the fourth variable was treated as a control parameter. Then we discussed how a canard-mediated slow passage in the 4D model explains the sub-threshold oscillatory behavior which cannot be reproduced by any of the 3D models, giving rise to mixed-mode bursting oscillations (MMBOs); see 12. Finally, we related the canard-mediated slow passage to the intervals of burst and silent phase which have been linked to the blockade of glutamatergic or GABAergic/glycinergic synapses over a wide range of developmental stages 69.This work has been published in Journal of Mathematical Biology and is available as 33.
5.5 Mathematical modeling of neuronal excitability
5.5.1 GABAergic neurons and Na V 1.1 channel hyperactivity: a novel neocortex-specific mechanism of Cortical Spreading Depression
Participants: Oana Chever, Sarah Zerimeh, Paolo Scalmani, Louisiane Lemaire, Alexandre Loucif, Marion Ayrault, Martin Krupa, Mathieu Desroches, Fabrice Duprat, Sandrine Cestèle, Massimo Mantegazza.
Cortical spreading depression (CSD) is a pathologic mechanism of migraine. We have identified a novel neocortex-specific mechanism of CSD initiation and a novel pathological role of GABAergic neurons. Mutations of the sodium channel (the SCN1A gene), which is particularly important for GABAergic neurons’ excitability, cause Familial Hemiplegic Migraine type-3 (FHM3), a subtype of migraine with aura. They induce gain-of-function of and hyperexcitability of GABAergic interneurons in culture. However, the mechanism linking these dysfunctions to CSD and FHM3 has not been elucidated. Here, we show that gain-of-function, induced by the specific activator Hm1a, or mimicked by optogenetic-induced hyperactivity of cortical GABAergic neurons, is sufficient to ignite CSD by spiking-generated extracellular build-up. This mechanism is neocortex specific because, with these approaches, CSD was not generated in other brain areas. GABAergic and glutamatergic synaptic transmission is not required for optogenetic CSD initiation, but glutamatergic transmission is implicated in CSD propagation. Thus, our results reveal the key role of hyper-activation of and GABAergic neurons in a novel mechanism of CSD initiation, which is relevant for FHM3 and possibly also for other types of migraine.This work has been submitted for publication and is available as 43.
The extension of this work is the topic of the PhD of Louisiane Lemaire, who started in October 2018. A first part of Louisiane's PhD has been to improve and extend the model published in 10 in a number of ways: replace the GABAergic neuron model used in 10, namely the Wang-Buszáki model, by a more recent fast-spiking cortical interneuron model due to Golomb and collaborators; implement the effect of the HM1a toxin used by M. Mantegazza to mimic the genetic mutation of sodium channels responsible for the hyperactivity of the GABAergic neurons; take into account ionic concentration dynamics (relaxing the hypothesis of constant reversal potentials) for the GABAergic as well whereas in 10 this was done only for the Pyramidal neuron. Furthermore, another mutation of this sodium channel leads to hyperactivity of the pyramidal neurons in a way that is akin to epileptiform activity. The model by Louisiane Lemaire has been extended in order to account for this pathological scenario as well. This required a great deal of modelling and calibration and the simulation results are closer to the actual experiments by Mantegazza than in our previous study. A manuscript is about to be submitted.
5.6 Mathematical modeling of memory processes
5.6.1 Neuronal mechanisms for sequential activation of memory items: Dynamics and reliability
Participants: Elif Köksal Ersöz, Carlos Aguilar Melchor, Pascal Chossat, Martin Krupa, Frédéric Lavigne.
In this article we present a biologically inspired model of activation of memory items in a sequence. Our model produces two types of sequences, corresponding to two different types of cerebral functions: activation of regular or irregular sequences. The switch between the two types of activation occurs through the modulation of biological parameters, without altering the connectivity matrix. Some of the parameters included in our model are neuronal gain, strength of inhibition, synaptic depression and noise. We investigate how these parameters enable the existence of sequences and influence the type of sequences observed. In particular we show that synaptic depression and noise drive the transitions from one memory item to the next and neuronal gain controls the switching between regular and irregular (random) activation.This work has been published in PLoS one and is available as 32.
5.7 Modelling the visual system
5.7.1 A sub-Riemannian model of the visual cortex with frequency and phase
Participants: Emre Baspinar, Alessandro Sarti, Giovanna Citti.
In this paper we present a novel model of the primary visual cortex (V1) based on orientation, frequency and phase selective behavior of the V1 simple cells. We start from the first level mechanisms of visual perception: receptive profiles. The model interprets V1 as a fiber bundle over the 2-dimensional retinal plane by introducing orientation, frequency and phase as intrinsic variables. Each receptive profile on the fiber is mathematically interpreted as a rotated, frequency modulated and phase shifted Gabor function. We start from the Gabor function and show that it induces in a natural way the model geometry and the associated horizontal connectivity modeling the neural connectivity patterns in V1. We provide an image enhancement algorithm employing the model framework. The algorithm is capable of exploiting not only orientation but also frequency and phase information existing intrinsically in a 2-dimensional input image. We provide the experimental results corresponding to the enhancement algorithm.This work has been published in The Journal of Mathematical Neuroscience and is available as 23.
6 Partnerships and cooperations
6.1 International initiatives
6.1.1 Inria associate team not involved in an IIL
NeuroTransSF
- Title: NeuroTransmitter cycle: A Slow-Fast modeling approach
- Duration: 2019 - 2022
- Coordinator: Mathieu Desroches
-
Partners:
- Mathematical, Computational and Experimental Neuroscience (MCEN) research group, Basque Center for Applied Mathematics (BCAM) (Spain)
- Inria contact: Mathieu Desroches
- Summary: This associated team project proposes to deepen the links between two young research groups, on strong Neuroscience thematics. This project aims to start from a joint work in which we could successfully model synaptic transmission delays for both excitatory and inhibitory synapses, matching experimental data, and to supplant it in two distinct directions. On the one hand, by modeling the endocytosis so as to obtain a complete mathematical formulation of the presynaptic neurotransmitter cycle, which will then be integrated within diverse neuron models (in particular interneurons) hence allowing a refined analysis of their excitability and short-term plasticity properties. On the other hand, by modeling the postsynaptic neurotransmitter cycle in link with long-term plasticity and memory. We will incorporate these new models of synapse in different types of neuronal networks and we will then study their excitability, plasticity and synchronisation properties in comparison with classical models. This project will benefit from strong experimental collaborations (UCL, Alicante) and it is coupled to the study of brain pathologies linked with synaptic dysfunctions, in particular certain early signs of Alzheimer's Disease. Our initiative also contains a training aspect with two PhD student involved as well as a series of mini-courses which we will propose to the partner institute on this research topic; we will also organise a "wrap-up" workshop in Sophia at the end of it. Finally, the project is embedded within a strategic tightening of our links with Spain with the objective of pushing towards the creation of a Southern-Europe network for Mathematical, Computational and Experimental Neuroscience, which will serve as a stepping stone in order to extend our influence beyond Europe. The webpage of the associated team is here. It contains the latest developments and new collaborations that have emerged from this project.
6.2 International research visitors
6.2.1 Visits of international scientists
As part of the NeuroTransSF associated team, Prof. Serafim Rodrigues (BCAM) has visited the MathNeuro team in February 2020 and in October 2020, for two weeks each time.
6.2.2 Visits to international teams
- Mathieu Desroches and Emre Baspinar have visited VU Amsterdam (Netherlands) to work with external collaborator Dr. Daniele Avitabile on their joint projects related to multiple-timescale dynamics of neuronal networks and their mean-field limits (see Results), in the context of the Human Brain Project SGA2 initiative. Two visits were organised, in February 2020 and in October 2020.
- Mathieu Desroches visited Prof. Serafim Rodrigues in the context of the NeuroTransSF associated team in July, August and September 2020. Two visits were funded by the associated team, the last one was funded by BCAM.
6.3 European initiatives
6.3.1 FP7 & H2020 Projects
HBP SGA2
- Title: Human Brain Project Specific Grant Agreement 3
- Duration: 3 years (March 2020 - March 2023)
- Coordinator: EPFL
- Partners: See the webpage of the project. Olivier Faugeras is leading the task T4.1.3 entitled “Meanfield and population models” of the Worpackage W4.1 “Bridging Scales”.
- Inria contact: Romain Veltz
- Summary: Understanding the human brain is one of the greatest challenges facing 21st century science. If we can rise to the challenge, we can gain profound insights into what makes us human, develop new treatments for brain diseases and build revolutionary new computing technologies. Today, for the first time, modern ICT has brought these goals within sight. The goal of the Human Brain Project, part of the FET Flagship Programme, is to translate this vision into reality, using ICT as a catalyst for a global collaborative effort to understand the human brain and its diseases and ultimately to emulate its computational capabilities. The Human Brain Project will last ten years and will consist of a ramp-up phase (from month 1 to month 36) and subsequent operational phases. This Grant Agreement covers the ramp-up phase. During this phase the strategic goals of the project will be to design, develop and deploy the first versions of six ICT platforms dedicated to Neuroin- formatics, Brain Simulation, High Performance Computing, Medical Informatics, Neuromorphic Computing and Neurorobotics, and create a user community of research groups from within and outside the HBP, set up a European Institute for Theoretical Neuroscience, complete a set of pilot projects providing a first demonstration of the scientific value of the platforms and the Institute, develop the scientific and technological capabilities required by future versions of the platforms, implement a policy of Responsible Innovation, and a programme of transdisciplinary education, and develop a framework for collaboration that links the partners under strong scientific leadership and professional project management, providing a coherent European approach and ensuring effective alignment of regional, national and European research and programmes. The project work plan is organized in the form of thirteen subprojects, each dedicated to a specific area of activity. A significant part of the budget will be used for competitive calls to complement the collective skills of the Consortium with additional expertise.
6.4 National initiatives
-
ANR ChaMaNe, "Enjeux mathématiques issus des neurosciences", duration: 4 years, Coordinator Name : Delphine Salort (Sorbonne Université). Webpages: webpage on the ANR website, Project webpage.
Partners' list:
- Partner 1 (CQB Biologie Computationnelle et Quantitative, Sorbonne Université, France);
- Partner 2 (LJAD, Université Côte d'Azur, France)
7 Dissemination
7.1 Promoting scientific activities
7.1.1 Scientific events: organisation
General chair, scientific chair
- Fabien Campillo is a founding member of the African scholarly Society on Digital Sciences (ASDS).
Member of the organizing committees
- Mathieu Desroches was a member of the organizing committee of the online international conference “Dynamics Days Digital 2020”, which took place on 24-27 August 2020 and gathered online about 600 participants.
- Mathieu Desroches is member of the organizing committee of the international conference “Dynamics Days Europe” 2021, to be held in Nice on 23-27 August 2021 [postponed from 2020 due to the covid-19 pandemic].
- Mathieu Desroches is member of the organzing committee of the “Bilbao Neuroscience and Computational Biology Workshop”, to be held in Bilbao on 1-4 June 2021 [postponed from 2020 due to the covid-19 pandemic].
- Louisiane Lemaire is a member of the organizing committee of the PhD Seminar of the Inria Sophia Antipolis Méditerranée Research Centre.
- Halgurd Taher is a member of the organizing committee of the PhD Seminar of the Inria Sophia Antipolis Méditerranée Research Centre.
- Romain Veltz is member of the advisory board of ICMNS (International conference on Mathematical Neuroscience)
7.1.2 Journal
Member of the editorial boards
- Mathieu Desroches is Review Editor of the journal Frontiers in Physiology (Impact Factor 3.4).
- Mathieu Desroches was Guest Editor of the journal Communications in Nonlinear Science and Numerical Simulation (Impact Factor 4.1) for a special issue on "Excitable dynamics in neural and cardiac systems", published in July 2020.
- Olivier Faugeras has created a new open access journal, Mathematical Neuroscience and Applications, under the diamond model (no charges for authors and readers) supported by Episciences.
- Romain Veltz is member of the Editorial Board of the journal Mathematical Neurosciences and Applications.
Reviewer - reviewing activities
- Fabien Campillo acts as a reviewer for Journal of Mathematical Biology.
- Mathieu Desroches acts as a reviewer for SIAM Journal on Applied Dynamical Systems (SIADS), Journal of Mathematical Biology, PLoS Computational Biology, Journal of Nonlinear Science, Nonlinear Dynamics, Physica D, Journal of Mathematical Neuroscience.
- Martin Krupa acts as a reviewer for Proceedings of the National Academy of Sciences of the USA (PNAS) and SIADS.
- Romain Veltz acts as a reviewer for Neural Computation, eLife, SIADS, PNAS, Journal of the Royal Society Interface, Plos Computational Biology, Journal of Mathematical Neurosciences, Acta Applicandae Mathematicae.
7.1.3 Invited talks
- Emre Baspinar gave a talk entitled “Elliptic bursting and torus canards: singular limits, single-cell models, network and mean-field models” at the online conference Dynamical Days Digital 2020, 24 August 2020.
- Mathieu Desroches gave a talk entitled “Slow-fast analysis of neural bursters: old and new” at the Modelife Workshop: Non-linear dynamics in neuroscience, Université Côte d'Azur (Nice), 4 March 2020.
- Mathieu Desroches gave a webinar talk entitled “Slow-fast analysis of neural bursters” at the Centre for Applied Mathematics in Bioscience and Medicine (CAMBAM), McGill University, 22 May 2020.
- Louisiane Lemaire gave a talk entitled “Mathematical modeling of the mutations of a sodium channel causing either migraine or epilepsy” at the online conference Dynamical Days Digital 2020, 25 August 2020.
- Yuri Rodrigues gave a talk entitled “Protein dynamics in synaptic plasticity prediction” at the online conference Dynamical Days Digital 2020, 25 August 2020.
- Halgurd Taher gave a talk entitled “Multi-timescale analysis of a neural mass model with short-term synaptic plasticity” at the online conference Dynamical Days Digital 2020, 25 August 2020.
- Halgurd Taher presented a poster entitled “Exact neural mass model for synaptic-based working memory” at the online Bernstein Conference 2020, 1 October 2020.
- Halgurd Taher gave a talk entitled “Exact neural mass model for synaptic-based working memory” at the online satellite workshop “Exact mean field formulation of complex (neural) networks” of the Complex Systems Society 2020 Conference, 9 December 2020.
- Halgurd Taher gave a talk entitled “The magical number 5” at the PhD seminar of the Inria Sophia Antipolis Méditerranée Research Center, 14 December 2020.
- Romain Veltz gave a talk entitled “Analysis of a neural field model for color perception unifying assimilation and contrast” at the Modelife Workshop: Non-linear dynamics in neuroscience, Université Côte d'Azur (Nice), 4 March 2020.
- Romain Veltz gave a talk at The Canadian Mathematical Society Winter Meeting in December 2020, "Mean field study of stochastic spiking neural networks"
- Romain Veltz gave a talk at Colloqium MAP5 Université Paris Descartes in January 2021, "Some recent results on models of networks of spiking neurons"
7.1.4 Scientific expertise
- Fabien Campillo was member of the local committee in charge of the scientific selection of visiting scientists (Comité NICE).
- Mathieu Desroches was on the Advisory Board of the Complex Systems Academy of the UCA JEDI Idex.
7.2 Teaching - Supervision - Juries
7.2.1 Teaching
- Master: Emre Baspinar, Dynamical Systems in the context of neuron models, (Lectures, example classes and computer labs), 3 hours (Dec. 2020), M1 (Mod4NeuCog), Université Côte d'Azur, Sophia Antipolis, France.
- Master: Mathieu Desroches, Modèles Mathématiques et Computationnels en Neuroscience (Lectures, example classes and computer labs), 12 hours, M1 (BIM), Sorbonne Université, Paris, France.
- Master: Mathieu Desroches, Dynamical Systems in the context of neuron models, (Lectures, example classes and computer labs), 8 hours (Jan. 2020) and 10 hours (Nov.-Dec. 2020), M1 (Mod4NeuCog), Université Côte d'Azur, Sophia Antipolis, France.
- Master: Romain Veltz, Mathematical Methods for Neurosciences, 20 hours, M2 (MVA), Sorbonne Université, Paris, France.
- Spring School: Romain Veltz gave a lecture on “Meanfield models of stochastic spiking neural networks” at the EITN spring school, Paris, 2020, invited by Alain Destexhe.
7.2.2 Supervision
- PhD in progress : Louisiane Lemaire, “Multi-scale mathematical modeling of cortical spreading depression”, started in October 2018, co-supervised by Mathieu Desroches and Martin Krupa.
- PhD in progress: Yuri Rodrigues, “Towards a model of post synaptic excitatory synapse”, started in March 2018, co-supervised by Romain Veltz and Hélène Marie (IPMC, Sophia Antipolis).
- PhD in progress: Halgurd Taher, “Next generation neural-mass models”, started in November 2018, co-supervised by Mathieu Desroches and Simona Olmi.
- PhD in progress: Guillaume Girier, “Mathematical, computational and experimental study of neural excitability”, started in October 2020, based in BCAM - Basque Center for Applied Mathematics (Bilbao, Spain), co-supervised by Serafim Rodrigues (BCAM) and Mathieu Desroches. Co-tutelle agreement between the University of the Basque Country (UPV-EHU) and the Université Côte d'Azur (UCA) in progress.
- PhD defended on 15 January 2021: Quentin Cormier, “Biological spiking neural networks”, started in September 2017, co-supervised by Romain Veltz and Etienne Tanré (Inria).
- PhD in progress: Pascal Helson, “Study of plasticity laws with stochastic processes”, started in September 2016, co-supervised by Romain Veltz and Etienne Tanré (Inria).
- PhD in progress: Samuel Nyobe, “Inférence dans les modèles de Markov cachés : Application en foresterie”, started in October 2017, co-supervised by Fabien Campillo, Serge Moto (University of Yaoundé, Camerun) and Vivien Rossi (CIRAD).
- Master 2 internship: Guillaume Girier, Master 2 student from the BIM-BMC Master of Sorbonne Université (Paris), March-June 2020, on “Integrator and resonator neurons: a new approach”, supervised by Mathieu Desroches and Boris Gutkin (ENS Paris).
- Master 1 internship: Mostafa Oukati Sadegh, Master 1 student of the MSc Mod4NeuCog (UCA) on “Bringing statistical inference to mechanistic models of neural circuits”, supervised by Romain Veltz.
7.2.3 Juries
- Romain Veltz was member of the Jury (as co-supervisor with E. Tanré) of the PhD of Quentin Cormier (Inria Sophia Antipolis) entitled "Long time behavior of a mean-field model of interacting spiking neurons", Inria Sophia Antipolis, 15 January 2021.
8 Scientific production
8.1 Major publications
- 1 articleLatching dynamics in neural networks with synaptic depressionPLoS ONE128August 2017, e0183710
- 2 articleSpatiotemporal canards in neural field equationsPhysical Review E 954April 2017, 042205
- 3 articleMean-field description and propagation of chaos in networks of Hodgkin-Huxley neuronsThe Journal of Mathematical Neuroscience212012, URL: http://www.mathematical-neuroscience.com/content/2/1/10
- 4 article A sub-Riemannian model of the visual cortex with frequency and phase The Journal of Mathematical Neuroscience 10 1 December 2020
- 5 articleLinks between deterministic and stochastic approaches for invasion in growth-fragmentation-death modelsJournal of mathematical biology736-72016, 1781--1821URL: https://hal.science/hal-01205467
- 6 articleWeak convergence of a mass-structured individual-based modelApplied Mathematics & Optimization7212015, 37--73URL: https://hal.inria.fr/hal-01090727
- 7 articleAnalysis and approximation of a stochastic growth model with extinctionMethodology and Computing in Applied Probability1822016, 499--515URL: https://hal.science/hal-01817824
- 8 articleEffect of population size in a predator--prey modelEcological Modelling2462012, 1--10URL: https://hal.inria.fr/hal-00723793
- 9 articleShort-term synaptic plasticity in the deterministic Tsodyks-Markram model leads to unpredictable network dynamicsProceedings of the National Academy of Sciences of the United States of America 110412013, 16610-16615
- 10 article Modeling cortical spreading depression induced by the hyperactivity of interneurons Journal of Computational Neuroscience October 2019
- 11 articleCanards, folded nodes and mixed-mode oscillations in piecewise-linear slow-fast systemsSIAM Review584accepted for publication in SIAM Review on 13 August 2015November 2016, 653-691
- 12 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave bursterChaos234October 2013, 046106
- 13 article Hopf bifurcation in a nonlocal nonlinear transport equation stemming from stochastic neural dynamics Chaos February 2017
- 14 unpublishedCanard-induced complex oscillations in an excitatory networkNovember 2018, working paper or preprint
- 15 articleTime-coded neurotransmitter release at excitatory and inhibitory synapsesProceedings of the National Academy of Sciences of the United States of America 1138February 2016, E1108-E1115
- 16 unpublishedA new twist for the simulation of hybrid systems using the true jump methodDecember 2015, working paper or preprint
- 17 articleA Center Manifold Result for Delayed Neural Fields EquationsSIAM Journal on Mathematical Analysis4532013, 1527-1562
- 18 article A center manifold result for delayed neural fields equations SIAM Journal on Applied Mathematics (under revision) RR-8020 July 2012
- 19 articleInterplay Between Synaptic Delays and Propagation Delays in Neural Field EquationsSIAM Journal on Applied Dynamical Systems1232013, 1566-1612
8.2 Publications of the year
International journals
International peer-reviewed conferences
Reports & preprints
8.3 Other
Softwares
8.4 Cited publications
- 50 articleHunting French ducks in a noisy environmentJournal of Differential Equations25292012, 4786--4841
- 51 book Noise-induced phenomena in slow-fast dynamical systems: a sample-paths approach Springer Science & Business Media 2006
- 52 articleTheory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortexThe Journal of Neuroscience211982, 32--48
- 53 articleHyperbolic planforms in relation to visual edges and textures perceptionPLoS Computational Biology5122009, e1000625
- 54 articleA role for fast rhythmic bursting neurons in cortical gamma oscillations in vitroProceedings of the National Academy of Sciences of the United States of America101182004, 7152--7157
- 55 articleMixed-Mode Oscillations with Multiple Time ScalesSIAM Review542May 2012, 211-288
- 56 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave bursterChaos234October 2013, 046106
- 57 articleThe geometry of slow manifolds near a folded nodeSIAM Journal on Applied Dynamical Systems742008, 1131--1162
- 58 articleLimiting curves for iid recordsThe Annals of Probability1995, 852--878
- 59 book Mathematical foundations of neuroscience 35 Springer 2010
- 60 articleA large deviation principle and an expression of the rate function for a discrete stationary gaussian processEntropy16122014, 6722--6738
- 61 book Dynamical systems in neuroscience MIT press 2007
- 62 articleNeural excitability, spiking and burstingInternational Journal of Bifurcation and Chaos10062000, 1171--1266
- 63 articleMixed-mode oscillations in a three time-scale model for the dopaminergic neuronChaos: An Interdisciplinary Journal of Nonlinear Science1812008, 015106
- 64 articleRelaxation oscillation and canard explosionJournal of Differential Equations17422001, 312--368
- 65 articleAmyloid precursor protein: from synaptic plasticity to Alzheimer's diseaseAnnals of the New York Academy of Sciences104812005, 149--165
- 66 articlePathophysiology of migraineAnnual review of physiology752013, 365--391
- 67 articleDifferential control of active and silent phases in relaxation models of neuronal rhythmsJournal of computational neuroscience2132006, 307--328
- 68 articleQuantifying the relative contributions of divisive and subtractive feedback to rhythm generationPLoS computational biology742011, e1001124
- 69 articleThe role of activity-dependent network depression in the expression and self-regulation of spontaneous activity in the developing spinal cordJournal of Neuroscience21222001, 8966--8978
- 70 articleModeling of spontaneous activity in developing spinal cord using activity-dependent depression in an excitatory networkJournal of Neuroscience2082000, 3041--3056
- 71 article A Markovian event-based framework for stochastic spiking neural networks Journal of Computational Neuroscience 30 April 2011
- 72 articleNeural Mass Activity, Bifurcations, and EpilepsyNeural Computation2312December 2011, 3232--3286
- 73 articleA Center Manifold Result for Delayed Neural Fields EquationsSIAM Journal on Mathematical Analysis4532013, 1527-562
- 74 articleLocal/Global Analysis of the Stationary Solutions of Some Neural Field EquationsSIAM Journal on Applied Dynamical Systems93August 2010, 954--998URL: http://arxiv.org/abs/0910.2247
- 75 articleDynamical diseases of brain systems: different routes to epileptic seizuresIEEE transactions on biomedical engineering5052003, 540--548

