Keywords
Computer Science and Digital Science
- A2.1.1. Semantics of programming languages
- A2.1.4. Functional programming
- A2.1.6. Concurrent programming
- A2.1.10. Domain-specific languages
- A2.1.11. Proof languages
- A2.4.2. Model-checking
- A2.4.3. Proofs
- A6.2.1. Numerical analysis of PDE and ODE
- A7.2. Logic in Computer Science
- A7.2.1. Decision procedures
- A7.2.2. Automated Theorem Proving
- A7.2.3. Interactive Theorem Proving
- A7.2.4. Mechanized Formalization of Mathematics
- A8.10. Computer arithmetic
Other Research Topics and Application Domains
- B5.2.2. Railway
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B6.1. Software industry
- B9.5.1. Computer science
- B9.5.2. Mathematics
1 Team members, visitors, external collaborators
Research Scientists
- Claude Marché [Team leader, Inria, Senior Researcher, HDR]
- Sylvie Boldo [Inria, Senior Researcher, HDR]
- Jean-Christophe Filliâtre [CNRS, Senior Researcher, HDR]
- Guillaume Melquiond [Inria, Researcher, HDR]
Faculty Members
- Sylvain Conchon [Univ Paris-Saclay, Professor, HDR]
- Andrei Paskevich [Univ Paris-Saclay, Associate Professor]
PhD Students
- Louise Ben Salem-Knapp [CEA DAM, from Oct 2020]
- Xavier Denis [Univ Paris-Saclay, from Oct 2020]
- Diane Gallois-Wong [Univ Paris-Saclay]
- Quentin Garchery [Univ Paris-Saclay]
- Antoine Lanco [Inria]
- Clément Pascutto [Taridès, CIFRE, from Jun 2020]
- Raphaël Rieu-Helft [TrustInSoft, CIFRE]
Technical Staff
- Benedikt Becker [Inria, Engineer]
- Cláudio Loureno [Inria, Engineer]
Interns and Apprentices
- Xavier Denis [Inria, from Mar 2020 until Aug 2020]
Administrative Assistants
- Katia Evrat [Inria, Until Sep 2020]
- Alexandra Merlin [Inria, from Oct 2020]
External Collaborators
- Thibaut Balabonski [Univ Paris-Saclay]
- Chantal Keller [Univ Paris-Saclay]
2 Overall objectives
2.1 Presentation
The general objective of the Toccata project is to promote formal
specification and computer-assisted proof in the development of
software that requires high assurance in terms of safety and
correctness with respect to its intended behavior.
Such safety-critical software appears in many application domains like
transportation (e.g., aviation, aerospace, railway, and more and more in cars),
communication (e.g., internet, smartphones), health devices, etc. The
number of tasks performed by software is quickly increasing, together
with the number of lines of code involved. Given the need of high
assurance of safety in the functional behavior of such applications,
the need for automated (i.e., computer-assisted) methods and
techniques to bring guarantee of safety became a major challenge. In
the past and at present, the most widely used approach to check safety
of software is to apply heavy test campaigns, which take a
large part of the costs of software development. Yet they cannot
ensure that all the bugs are caught, and remaining bugs may have
catastrophic causes (e.g., the Heartbleed bug in OpenSSL library
discovered in 2014 https://
Generally speaking, software verification approaches pursue three goals: (1) verification should be sound, in the sense that no bugs should be missed, (2) verification should not produce false alarms, or as few as possible, (3) it should be as automatic as possible. Reaching all three goals at the same time is a challenge. A large class of approaches emphasizes goals (2) and (3): testing, run-time verification, symbolic execution, model checking, etc. Static analysis, such as abstract interpretation, emphasizes goals (1) and (3). Deductive verification emphasizes (1) and (2). The Toccata project is mainly interested in exploring the deductive verification approach, although we also consider the other ones in some cases.
In the past decade, there have been significant progress made in the domain of deductive program verification. They are emphasized by some success stories of application of these techniques on industrial-scale software. For example, the Atelier B system was used to develop part of the embedded software of the Paris metro line 14 39 and other railway-related systems; a formally proved C compiler was developed using the Coq proof assistant 56; the L4-verified project developed a formally verified micro-kernel with high security guarantees, using analysis tools on top of the Isabelle/HOL proof assistant 55. A bug in the JDK implementation of TimSort was discovered using the KeY environment 62 and a fixed version was proved sound. Another sign of recent progress is the emergence of deductive verification competitions (e.g., VerifyThis 1). Finally, recent trends in the industrial practice for development of critical software is to require more and more guarantees of safety, e.g., the new DO-178C standard for developing avionics software adds to the former DO-178B the use of formal models and formal methods. It also emphasizes the need for certification of the analysis tools involved in the process.
3 Research program
Panorama of Deductive Verification
There are two main families of approaches for deductive verification. Methods in the first family build on top of mathematical proof assistants (e.g., Coq, Isabelle) in which both the model and the program are encoded; the proof that the program meets its specification is typically conducted in an interactive way using the underlying proof construction engine. Methods from the second family proceed by the design of standalone tools taking as input a program in a particular programming language (e.g., C, Java) specified with a dedicated annotation language (e.g., ACSL 36, JML 45) and automatically producing a set of mathematical formulas (the verification conditions) which are typically proved using automatic provers (e.g., Z3 63, Alt-Ergo 48, CVC4 35).
The first family of approaches usually offers a higher level of assurance than the second, but also demands more work to perform the proofs (because of their interactive nature) and makes them less easy to adopt by industry. Moreover, they generally do not allow to directly analyze a program written in a mainstream programming language like Java or C. The second kind of approaches has benefited in the past years from the tremendous progress made in SAT and SMT solving techniques, allowing more impact on industrial practices, but suffers from a lower level of trust: in all parts of the proof chain (the model of the input programming language, the VC generator, the back-end automatic prover), potential errors may appear, compromising the guarantee offered. Moreover, while these approaches are applied to mainstream languages, they usually support only a subset of their features.
Overall Goals of the Toccata Project
One of our original skills is the ability to conduct proofs by using automatic provers and proof assistants at the same time, depending on the difficulty of the program, and specifically the difficulty of each particular verification condition. We thus believe that we are in a good position to propose a bridge between the two families of approaches of deductive verification presented above. Establishing this bridge is one of the goals of the Toccata project: we want to provide methods and tools for deductive program verification that can offer both a high amount of proof automation and a high guarantee of validity. Indeed, an axis of research of Toccata is the development of languages, methods and tools that are themselves formally proved correct. Recent advances in the foundations of deductive verification include various aspects such as reasoning efficiently on bitvector programs 7 or providing counterexamples when a proof does not succeed 49.
A specifically challenging aspect of deductive verification methods is how one does deal with memory mutation in general, an issue that appear under various similar form such the reasoning on mutable data structures or on concurrent programs, with the common denominator of the tracking of memory change on shared data. The ability to track aliasing is also a key for the ability of specifying programs and conduct proofs using the advanced notion of ghost code6.
In industrial applications, numerical calculations are very common (e.g. control software in transportation). Typically they involve floating-point numbers. Some of the members of Toccata have an internationally recognized expertise on deductive program verification involving floating-point computations. Our past work includes a new approach for proving behavioral properties of numerical C programs using Frama-C/Jessie 34, various examples of applications of that approach 43, the use of the Gappa solver for proving numerical algorithms 61, an approach to take architectures and compilers into account when dealing with floating-point programs 44, 60. We contributed to the CompCert verified compiler, regarding the support for floating-point operations 2. We also contributed to the Handbook of Floating-Point Arithmetic 59. A representative case study is the analysis and the proof of both the method error and the rounding error of a numerical analysis program solving the one-dimension acoustic wave equation 4140. We published a reference book on the verification of floating-point algorithms with Coq 3. Our experience led us to a conclusion that verification of numerical programs can benefit a lot from combining automatic and interactive theorem proving 42, 43, 50. Verification of numerical programs is another main axis of Toccata.
Deductive program verification methods are built upon theorem provers to decide whether a expected proof obligation on a program is a valid mathematical proposition, hence working on deductive verification requires a certain amount of work on the aspect of design of theorem provers. We are involved in particular in the Alt-Ergo SMT solver, for which we designed an original approach for reasoning on arithmetic facts 510 ; and the Gappa tool dedicated to reasoning on rounding errors in floating-point computations 8. Proof by reflection is also a powerful approach for advanced reasoning about programs 9.
In the past, we have been more and more involved in the development of significantly large case studies and applications, such as for example the verification of matrix multiplication algorithms 4, the design of verified OCaml librairies 46, the realization of a platform for verification of shell scripts 37, or the correct-by-construction design of an efficient library for arbitrary-precision arithmetic 9.
Our scientific programme detailed below is structured into four axes:
- Foundations and spreading of deductive program verification;
- Reasoning on mutable memory in program verification;
- Verification of Computer Arithmetic;
- Spreading Formal Proofs.
Let us conclude with more general considerations about our agenda of the next four years: we want to keep on
- with general audience actions;
- industrial transfer, in particular through an extension of the perimeter of the ProofInUse joint lab.
3.1 Foundations and spreading of deductive program verification
Permanent researchers: S. Conchon, J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich
This axis covers the central theme of the team: deductive verification, from the point of view of its foundations but also our will to spread its use in software development. The general motto we want to defend is “deductive verification for the masses”. A non-exhaustive list of subjects we want to address is as follows.
- The verification of general-purpose algorithms and data structures: the challenge is to discover adequate invariants to obtain a proof, in the most automatic way as possible, in the continuation of the current VOCaL project and the various case studies presented in Axis 4 below.
- Uniform approaches to obtain correct-by-construction programs and libraries, in particular by automatic extraction of executable code (in OCaml, C, CakeML, etc.) from verified programs, and including innovative general methods like advanced ghost code, ghost monitoring, etc.
- Automated reasoning dedicated to deductive verification, so as to improve proof automation; improved combination of interactive provers and fully automated ones, proof by reflection.
- Improved feedback in case of proof failures: based on generation of counterexamples, or symbolic execution, or possibly randomized techniques à la quickcheck.
- Reduction of the trusted computing base in our toolchains: production of certificates from automatic proofs, for goal transformations (like those done by Why3), and from the generation of VCs
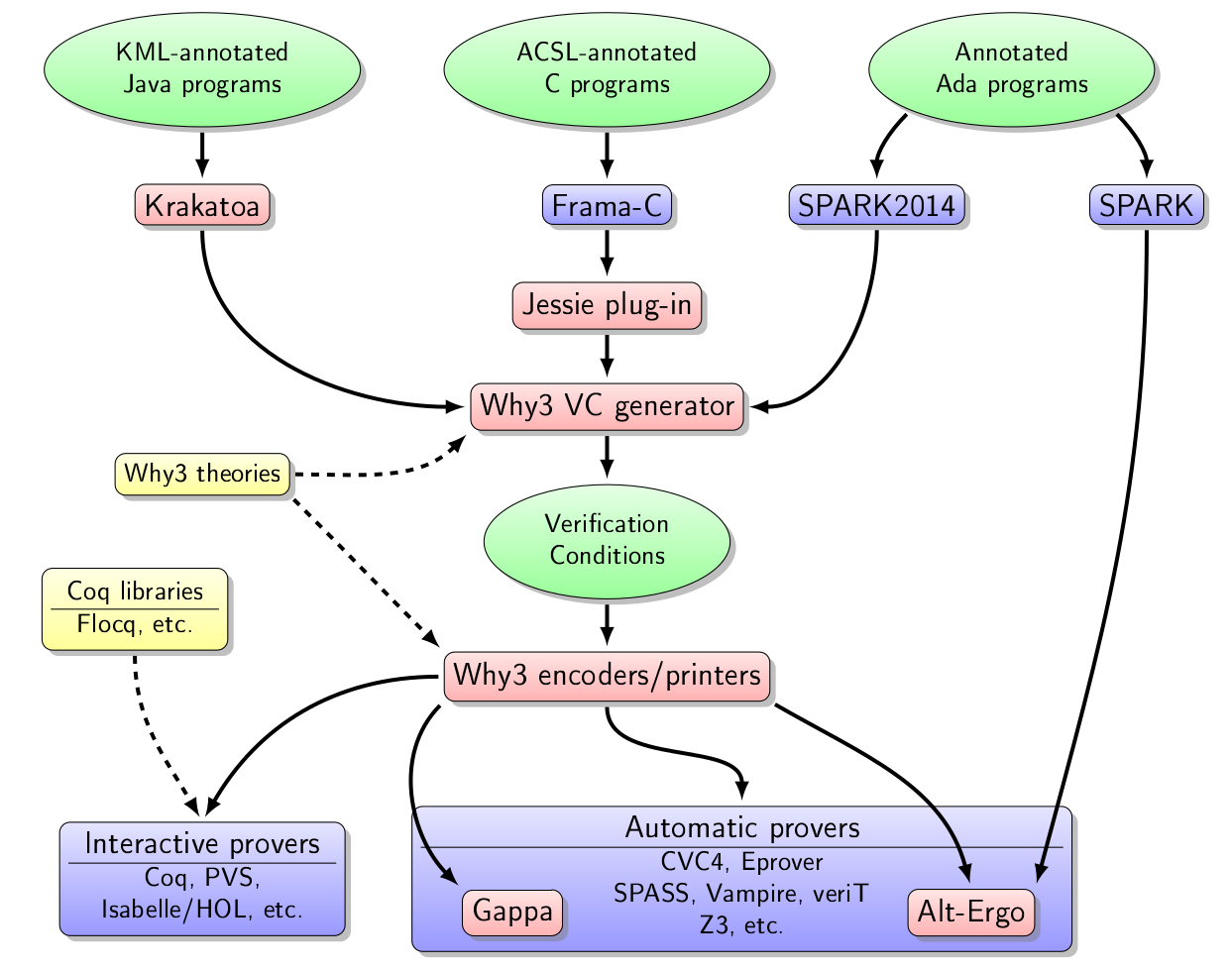
A significant part of the work achieved in this axis is related to the Why3 toolbox and its ecosystem, displayed on Figure 1. The boxes in red background correspond to the tools we develop in the Toccata team.
3.2 Reasoning on mutable memory in program verification
Permanent researchers: J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich
This axis concerns specifically the techniques for reasoning on programs where aliasing is the central issue. It covers the methods based on type-based alias analysis and related memory models, on specific program logics such as separation logics, and extended model-checking. It concerns the application on analysis of C or C++ codes, on Ada codes involving pointers, but also concurrent programs in general. The main topics planned are:
- The study of advanced type systems dedicated to verification, for controlling aliasing, and their use for obtaining easier-to-prove verification conditions. Modern typing system in the style of Rust, involving ownership and borrowing, will be considered.
- The design of front-ends of Why3 for the proofs of programs where aliasing cannot be fully controlled statically, via adequate memory models, aiming in particular at extraction to C; and also for concurrent programs.
- The continuation of fruitful work on concurrent parameterized systems, and its corresponding specific SMT-based model-checking.
- Concurrent programming on weak memory models, on one hand as an
extension of parameterized systems above, but also in the specific
context of OCaml multicore (http://
ocamllabs. ).io/ doc/ multicore. html - In particular in the context of the ProofInUse joint lab, design methods for Ada, C, C++ or Java using memory models involving fine-grain analysis of pointers. Rust programs could be considered as well.
3.3 Verification of Computer Arithmetic
Permanent researchers: S. Boldo, C. Marché, G. Melquiond
We of course want to keep this axis which is a major originality of Toccata. The main topics of the next 4 years will be:
- Fundamental studies concerning formalization of floating-point computations, algorithms, and error analysis. Related to numerical integration, we will develop the relationships between mathematical stability and floating-point stability of numerical schemes.
- A significant effort dedicated to verification of numerical programs written in C, Ada, C++. This involves combining specifications in real numbers and computation in floating-point, and underlying automated reasoning techniques with floating-point numbers and real numbers. A new approach we have in mind concerns some variant of symbolic execution of both code and specifications involving real numbers.
- We have not yet studied embedded systems. Our approach is first to tackle numerical filters. This requires more results on fixed-point arithmetic and a careful study of overflows.
- Also a specific focus on arbitrary precision integer arithmetic, in the continuation of the ongoing PhD thesis of R. Rieu-Helft.
3.4 Spreading Formal Proofs
Permanent researchers: S. Boldo, S. Conchon, J.-C. Filliâtre, C. Marché, G. Melquiond, A. Paskevich
This axis covers applications in general. The applications we currently have in mind are:
- Hybrid Systems, i.e., systems mixing discrete and continuous transitions. This theme covers many aspects such as general techniques for formally reasoning of differential equations, and extending SMT-based reasoning. The challenge is to support both abstract mathematical reasoning and concrete program execution (e.g., using floating-point representation). Hybrid systems will be a common effort with other members of the future laboratory joint with LSV of ENS Cachan.
- Applied mathematics, in the continuation of the current efforts towards verification of Finite Element Method. It has only been studied in the mathematical point of view during this period. We plan to also consider their floating-point behavior and a demanding application is that of molecular simulation exhibited in the new EMC2 project. The challenge here is both in the mathematics to be formalized, in the numerical errors that have never been studied (and that may be huge in specific cases), and in the size of the programs, which requires that our tools scale.
- Continuation of our work on analysis of shell scripts. The challenge is to be able to analyze a large number of scripts (more than 30,000 in the corpus of Debian packages installation scripts) in an automatic manner. An approach that will be considered is some form of symbolic execution.
- Explore proof tools for mathematics, in particular automated reasoning for real analysis (application: formalization of the weak Goldbach conjecture), and in number theory.
- Obtain and distribute verified OCaml libraries, as expected outcome of the VOCaL project.
- Formalization of abstract interpretation and WP calculi: in the continuation of the former project Verasco, and an ongoing project proposal joint with CEA List. The difficulty of achieving full verification of such tools will be mitigated by use of certificate techniques.
4 Application domains
The application domains we target involve safety-critical software, that is where a high-level guarantee of soundness of functional execution of the software is wanted. Currently our industrial collaborations or impact mainly belong to the domain of transportation: aerospace, aviation, railway, automotive.
Generally speaking, we believe that our increasing industrial impact is a representative success for our general goal of spreading deductive verification methods to a larger audience, and we are firmly engaged into continuing such kind of actions in the future.
4.1 Safety-Critical Software in Transportation
- Transfer to aeronautics: Airbus France Development of the control software of Airbus planes historically includes advanced usage of formal methods. A first aspect is the usage of the CompCert verified compiler for compiling C source code. Our work in cooperation with Gallium team for the safe compilation of floating-point arithmetic operations 2 is directly in application in this context. A second aspect is the usage of the Frama-C environment for static analysis to verify the C source code. In this context, both our tools Why3 and Alt-Ergo are indirectly used to verify C code.
-
Transfer to the community of Atelier B
In the former ANR
project BWare, we investigated the use of Why3 and Alt-Ergo as an
alternative back-end for checking proof obligations generated by
Atelier B, whose main applications are railroad-related
https://
www. . The transfer effort continues nowadays through the FUI project LCHIP.atelierb. eu/ en/ -
ProofInUse joint lab: transfer to the community of Ada
development
Through the creation of the ProofInUse joint lab (https://
www. ) in 2014, with AdaCore company (https://adacore. com/ proofinuse www. ), we have a growing impact on the community of industrial development of safety-critical applications written in Ada. See the web page https://adacore. com/ www. for a an overview of AdaCore's customer projects, in particular those involving the use of the SPARK Pro tool set. This impact involves both the use of Why3 for generating VCs on Ada source codes, and the use of Alt-Ergo for performing proofs of those VCs.adacore. com/ industries The impact of ProofInUse can also be measured in term of job creation: the first two ProofInUse engineers, D. Hauzar and C. Fumex, employed initially on Inria temporary positions, have now been hired on permanent positions in AdaCore company. It is also interesting to notice that this effort allowed AdaCore company to get new customers, in particular the domains of application of deductive formal verification went beyond the historical domain of aerospace: application in automotive (https://
www. ) cyber-security (https://adacore. com/ customers/ toyota-itc-japan www. ), health (artificial heart, https://adacore. com/ customers/ multi-level-security-workstation www. ).adacore. com/ customers/ total-artificial-heart
4.2 Classification Algorithms of the Parcoursup Platform
ParcourSup (https://
The expected properties of the algorithms in question are documented
in natural
language (https://
In the year 2019 we have been involved in a project for verification of these algorithms. The choice of the proof environment to prove the ParcourSup algorithms could have naturally turner to our Krakatoa tool 57, 58, dedicated to Java, but this one is rather old: it only supports version 1.4 of Java (the Java code of ParcoursSup requires version 8), and is not really maintained due to lack of users. Other similar proof environments exist in the world, such as KeY 32 and VeriFast 51, but these tools do not support Java version 8 yet. The most promising candidate was OpenJML 47, which supports Java version 8.
In addition, our experience in proof of programs leads us to think that to prove the ParcourSup code, it is better to begin to consider an abstraction of the Java code, written directly in the intermediate language of Why3, in order to focus from the start on writing formal specifications necessary, then the search for the invariants to insert in the coded. The analysis with Why3 of 1-rate only algorithm allowed to validate several of the properties stated in the specification.
Later on, an analysis of Java code with OpenJML identified risks of errors in execution due to capacity overrun in calculations arithmetic. The proof of absence of run-time errors in this code was not fully achieved, we had to modify the Java code slightly. The original code was correct, but beyond the capabilities of OpenJML. The proof of the functional behavior of the Java code (properties described in the specification document in French) could not be made due to OpenJML limitations.
We finally implemented a new protoype JML2Why3 to go further in the proof of functional properties of the Java code. No only we were able to obtain again the proof of absence of overflow arithmetic and no null pointer dereferencing, but we could formally establish the property that the final call order is indeed a permutation (hence a bijection) of the initial list of wishes: in particular, no candidate can be forgotten by the code.
A report details the conclusion of this analysis 29.
4.3 Formal Analysis of Debian packages
Impactful results were produced in the context of the CoLiS project for the formal analysis of Debian packages. A first important step was the version 2 of the design of the CoLiS language done by B. Becker, C. Marché and other co-authors 38, that includes a modified formal syntax, a extended formal semantics, together with the design of concrete and symbolic interpreters. Those interpreters are specified and implemented in Why3, proved correct (following the initial approach for the concrete interpreter published in 2018 52 and an approach for symbolic interpretation 37), and finally extracted to OCaml code.
To make the extracted code effective, it must be linked together with a library that implements a solver for feature constraints 54, and also a library that formally specifies the behavior of basic UNIX utilities. The latter library is documented in details in a research report 53.
A third result is a large verification campaign running the CoLiS toolbox on all the packages of the current Debian distribution. The results of this campaign were reported in another article 15 that was presented at TACAS conference in 2020. The most visible side effect of this experiment is the discovery of bugs: more than 150 bug reports have been filled against various Debian packages.
4.4 Extensions of ProofInUse joint lab
The current plans for continuation of the ProofInUse joint lab
(https://
5 Highlights of the year
5.1 Awards
- Raphaël Rieu-Helft obtained the “Distinguished Student
Author” award at the International Symposium on Symbolic and
Algebraic Computation (ISSAC) Conference
(https://
www. ) for his paper 21 written jointly with G. Melquiond. ISSAC is the top world conference on the domain of computer algebra.sigsam. org/ Awards/ ISSACAwards. html - The Why3 software was awarded the “prix coup de cœur du Hub Open Source Systematic”
https://
systematic-paris-region. org/ presse/ why3-laureat-du-prix-coup-de-coeur-academique-du-hub-open-source-du-pole-systematic/
6 New software and platforms
6.1 New software
6.1.1 Alt-Ergo
- Name: Automated theorem prover for software verification
- Keywords: Software Verification, Automated theorem proving
- Functional Description: Alt-Ergo is an automatic solver of formulas based on SMT technology. It is especially designed to prove mathematical formulas generated by program verification tools, such as Frama-C for C programs, or SPARK for Ada code. Initially developed in Toccata research team, Alt-Ergo's distribution and support are provided by OCamlPro since September 2013.
- Release Contributions: the "SAT solving" part can now be delegated to an external plugin, new experimental SAT solver based on mini-SAT, provided as a plugin. This solver is, in general, more efficient on ground problems, heuristics simplification in the default SAT solver and in the matching (instantiation) module, re-implementation of internal literals representation, improvement of theories combination architecture, rewriting some parts of the formulas module, bugfixes in records and numbers modules, new option "-no-Ematching" to perform matching without equality reasoning (i.e. without considering "equivalence classes"). This option is very useful for benchmarks coming from Atelier-B, two new experimental options: "-save-used-context" and "-replay-used-context". When the goal is proved valid, the first option allows to save the names of useful axioms into a ".used" file. The second one is used to replay the proof using only the axioms listed in the corresponding ".used" file. Note that the replay may fail because of the absence of necessary ground terms generated by useless axioms (that are not included in .used file) during the initial run.
-
URL:
http://
alt-ergo. lri. fr - Authors: Sylvain Conchon, Évelyne Contejean, Stéphane Lescuyer, Mohamed Iguernelala
- Contact: Sylvain Conchon
- Participants: Alain Mebsout, Évelyne Contejean, Mohamed Iguernelala, Stéphane Lescuyer, Sylvain Conchon
- Partner: OCamlPro
6.1.2 CoqInterval
- Name: Interval package for Coq
- Keywords: Interval arithmetic, Coq
-
Functional Description:
CoqInterval is a library for the proof assistant Coq.
It provides several tactics for proving theorems on enclosures of real-valued expressions. The proofs are performed by an interval kernel which relies on a computable formalization of floating-point arithmetic in Coq.
The Marelle team developed a formalization of rigorous polynomial approximation using Taylor models in Coq. In 2014, this library has been included in CoqInterval.
-
URL:
http://
coq-interval. gforge. inria. fr/ - Publications: hal-00180138, hal-00797913, hal-01086460, hal-01289616, hal-01630143
- Author: Guillaume Melquiond
- Contact: Guillaume Melquiond
- Participants: Assia Mahboubi, Érik Martin-Dorel, Guillaume Melquiond, Jean-Michel Muller, Laurence Rideau, Laurent Théry, Micaela Mayero, Mioara Joldes, Nicolas Brisebarre, Thomas Sibut-Pinote
6.1.3 Coquelicot
- Name: The Coquelicot library for real analysis in Coq
- Keywords: Coq, Real analysis
- Functional Description: Coquelicot is library aimed for supporting real analysis in the Coq proof assistant. It is designed with three principles in mind. The first is the user-friendliness, achieved by implementing methods of automation, but also by avoiding dependent types in order to ease the stating and readability of theorems. This latter part was achieved by defining total function for basic operators, such as limits or integrals. The second principle is the comprehensiveness of the library. By experimenting on several applications, we ensured that the available theorems are enough to cover most cases. We also wanted to be able to extend our library towards more generic settings, such as complex analysis or Euclidean spaces. The third principle is for the Coquelicot library to be a conservative extension of the Coq standard library, so that it can be easily combined with existing developments based on the standard library.
-
URL:
http://
coquelicot. saclay. inria. fr/ - Contact: Sylvie Boldo
- Participants: Catherine Lelay, Guillaume Melquiond, Sylvie Boldo
6.1.4 Cubicle
- Name: The Cubicle model checker modulo theories
- Keywords: Model Checking, Software Verification
- Functional Description: Cubicle is an open source model checker for verifying safety properties of array-based systems, which corresponds to a syntactically restricted class of parametrized transition systems with states represented as arrays indexed by an arbitrary number of processes. Cache coherence protocols and mutual exclusion algorithms are typical examples of such systems.
-
URL:
http://
cubicle. lri. fr/ - Contact: Sylvain Conchon
- Participants: Alain Mebsout, Sylvain Conchon
6.1.5 Flocq
- Name: The Flocq library for formalizing floating-point arithmetic in Coq
- Keywords: Floating-point, Arithmetic code, Coq
-
Functional Description:
The Flocq library for the Coq proof assistant is a comprehensive formalization of floating-point arithmetic: core definitions, axiomatic and computational rounding operations, high-level properties. It provides a framework for developers to formally verify numerical applications.
Flocq is currently used by the CompCert verified compiler to support floating-point computations.
-
URL:
http://
flocq. gforge. inria. fr/ - Publications: inria-00534854, hal-00743090, hal-00862689, hal-01091186, hal-01091189, hal-01632617
- Authors: Guillaume Melquiond, Sylvie Boldo
- Contacts: Sylvie Boldo, Guillaume Melquiond
- Participants: Guillaume Melquiond, Pierre Roux, Sylvie Boldo
6.1.6 Gappa
- Name: The Gappa tool for automated proofs of arithmetic properties
- Keywords: Floating-point, Arithmetic code, Software Verification, Constraint solving
- Functional Description: Gappa is a tool intended to help formally verifying numerical programs dealing with floating-point or fixed-point arithmetic. It has been used to write robust floating-point filters for CGAL and it is used to verify elementary functions in CRlibm. While Gappa is intended to be used directly, it can also act as a backend prover for the Why3 software verification plateform or as an automatic tactic for the Coq proof assistant.
-
URL:
https://
gappa. gitlabpages. inria. fr/ - Publications: inria-00070739, inria-00344518, inria-00070330, tel-01094485, inria-00071232, inria-00432726, ensl-00379167, ensl-00200830, hal-01110666, hal-01110669, hal-01632617
- Contact: Guillaume Melquiond
- Participant: Guillaume Melquiond
6.1.7 Why3
- Name: The Why3 environment for deductive verification
- Keywords: Formal methods, Trusted software, Software Verification, Deductive program verification
- Functional Description: Why3 is an environment for deductive program verification. It provides a rich language for specification and programming, called WhyML, and relies on external theorem provers, both automated and interactive, to discharge verification conditions. Why3 comes with a standard library of logical theories (integer and real arithmetic, Boolean operations, sets and maps, etc.) and basic programming data structures (arrays, queues, hash tables, etc.). A user can write WhyML programs directly and get correct-by-construction OCaml programs through an automated extraction mechanism. WhyML is also used as an intermediate language for the verification of C, Java, or Ada programs.
-
URL:
http://
why3. lri. fr/ - Authors: Jean-Christophe Filliâtre, Guillaume Melquiond, Claude Marché, Andriy Paskevych, François Bobot, Levs Gondelmans, Martin Clochard
- Contacts: Jean-Christophe Filliâtre, Claude Marché
- Participants: Andriy Paskevych, Claude Marché, François Bobot, Guillaume Melquiond, Jean-Christophe Filliâtre, Levs Gondelmans, Martin Clochard
- Partners: CNRS, Université Paris-Sud
6.1.8 Coq
- Name: The Coq Proof Assistant
- Keywords: Proof, Certification, Formalisation
- Scientific Description: Coq is an interactive proof assistant based on the Calculus of (Co-)Inductive Constructions, extended with universe polymorphism. This type theory features inductive and co-inductive families, an impredicative sort and a hierarchy of predicative universes, making it a very expressive logic. The calculus allows to formalize both general mathematics and computer programs, ranging from theories of finite structures to abstract algebra and categories to programming language metatheory and compiler verification. Coq is organised as a (relatively small) kernel including efficient conversion tests on which are built a set of higher-level layers: a powerful proof engine and unification algorithm, various tactics/decision procedures, a transactional document model and, at the very top an IDE.
- Functional Description: Coq provides both a dependently-typed functional programming language and a logical formalism, which, altogether, support the formalisation of mathematical theories and the specification and certification of properties of programs. Coq also provides a large and extensible set of automatic or semi-automatic proof methods. Coq's programs are extractible to OCaml, Haskell, Scheme, ...
-
Release Contributions:
Some highlights from this release are:
- Introduction of primitive persistent arrays in the core language, implemented using imperative persistent arrays.
- Introduction of definitional proof irrelevance for the equality type defined in the SProp sort.
- Many improvements to the handling of notations, including number notations, recursive notations and notations with bindings. A new algorithm chooses the most precise notation available to print an expression, which might introduce changes in printing behavior.
See the Zenodo citation https://
zenodo. for more information on this release.org/ record/ 4501022#. YB00r5NKjlw -
News of the Year:
Coq version 8.13 integrates many usability improvements, as well as extensions of the core language. The main changes include:
- Introduction of primitive persistent arrays in the core language, implemented using imperative persistent arrays.
- Introduction of definitional proof irrelevance for the equality type defined in the SProp sort.
- Cumulative record and inductive type declarations can now specify the variance of their universes.
- Various bugfixes and uniformization of behavior with respect to the use of implicit arguments and the handling of existential variables in declarations, unification and tactics.
- New warning for unused variables in catch-all match branches that match multiple distinct patterns.
- New warning for Hint commands outside sections without a locality attribute, whose goal is to eventually remove the fragile default behavior of importing hints only when using Require. The recommended fix is to declare hints as export, instead of the current default global, meaning that they are imported through Require Import only, not Require. See the following rationale and guidelines for details.
- General support for boolean attributes.
- Many improvements to the handling of notations, including number notations, recursive notations and notations with bindings. A new algorithm chooses the most precise notation available to print an expression, which might introduce changes in printing behavior.
- Tactic improvements in lia and its zify preprocessing step, now supporting reasoning on boolean operators such as Z.leb and supporting primitive integers Int63.
- Typing flags can now be specified per-constant / inductive.
- Improvements to the reference manual including updated syntax descriptions that match Coq's grammar in several chapters, and splitting parts of the tactics chapter to independent sections.
See the changelog for an overview of the new features and changes, along with the full list of contributors. https://
coq. github. io/ doc/ v8. 13/ refman/ changes. html#version-8-13 -
URL:
http://
coq. inria. fr/ - Authors: Bruno Barras, Yves Bertot, Frédéric Besson, Pierre Corbineau, Cristina Cornes, Judicaël Courant, Pierre Courtieu, Pierre Crégut, David Delahaye, Maxime Denes, Jean-Christophe Filliâtre, Julien Forest, Emilio Jesus Gallego Arias, Gaëtan Gilbert, Georges Gonthier, Benjamin Grégoire, Hugo Herbelin, Gérard Huet, Vincent Laporte, Pierre Letouzey, Assia Mahboubi, Pascal Manoury, Guillaume Melquiond, César Munoz, Chetan Murthy, Amokrane Saibi, Catherine Parent, Christine Paulin Mohring, Pierre-Marie Pédrot, Loïc Pottier, Matthieu Sozeau, Arnaud Spiwack, Enrico Tassi, Laurent Théry, Benjamin Werner, Théo Zimmermann
- Contacts: Hugo Herbelin, Matthieu Sozeau
- Participants: Yves Bertot, Frédéric Besson, Tej Chajed, Cyril Cohen, Pierre Corbineau, Pierre Courtieu, Maxime Denes, Jim Fehrle, Julien Forest, Emilio Jesús Gallego Arias, Gaëtan Gilbert, Georges Gonthier, Benjamin Grégoire, Jason Gross, Hugo Herbelin, Vincent Laporte, Olivier Laurent, Assia Mahboubi, Kenji Maillard, Érik Martin-Dorel, Guillaume Melquiond, Pierre-Marie Pédrot, Clément Pit-Claudel, Kazuhiko Sakaguchi, Vincent Semeria, Michael Soegtrop, Arnaud Spiwack, Matthieu Sozeau, Enrico Tassi, Laurent Théry, Anton Trunov, Li-Yao Xia, Théo Zimmermann
- Partners: CNRS, Université Paris-Sud, ENS Lyon, Université Paris-Diderot
7 New results
7.1 Foundations and Spreading of Deductive Program Verification
- Certificates for Logic Transformations In a context of formal program verification, using automatic provers, the trusted code base of verification environments is typically very broad. An environment such as Why3 implements many complex procedures: generation of verification conditions, logical transformations of proof tasks, and interactions with external provers. Considering only the logical transformations of Why3, their implementation already amounts to more than 17,000 lines of OCaml code. In order to increase our confidence in the correction of such a verification tool, Garchery, Keller, Marché and Paskevich 23 proposed a mechanism of certifying transformations, producing certificates that can be validated by an external tool, according to the skeptical approach. They explored two methods to validate certificates: one based on a dedicated verifier developed in OCaml, the other based on the universal proof checker Dedukti. A specificity of their certificates is to be “small grains” and composable, which makes the approach incremental, allowing to gradually add new certifying transformations.
-
Low Cost High Integrity Platform
The purpose of the LCHIP project 25 is to ease the development of SIL4 certified systems and software, and to drastically reduce costs associated with their development. To achieve this goal, LCHIP combines a complete development environment for the B formal language and a safety executing platform.
LCHIP avoids most testing by taking care of the verification of the software (type check, proof, compilation). The B method underlying this project enforces the development to be mathematically sound by producing proof obligations (PO). Those logical fomulas are expressed in first order logic extended with set theory and integer arithmetic. To target full proof automation of POs, the LCHIP platform integrates several automatic theorem provers. As a proof-of-concept, a connection to third-party provers has been conducted through the Why3 tool. This experiment produced excellent results in terms of proof automation, in particular for the Alt-Ergo prover.
- Simpler Proofs with Decentralized Invariants When verifying programs where the data have some recursive structure, it is natural to make use of global invariants that are themselves recursively defined. Though this is mathematically elegant, this makes the proofs more complex, as the preservation of these invariants now requires induction. In particular, this makes the proofs less amenable to automation. An alternative is to use local invariants attached to individual components of the structure and which only involve a bounded number of elements. These are called decentralized invariants. When the structure is updated, the footprint of the modification only impacts a bounded number of invariants and reestablishing them does not require induction. In this paper 13, Filliâtre illustrates this idea on three non-trivial programs, for which fully automated proofs are achieved.
- Abstraction and Genericity in Why3 The benefits of modularity in programming — abstraction barriers, which allow hiding implementation details behind an opaque interface, and genericity, which allows specializing a single implementation to a variety of underlying data types — apply just as well to deductive program verification, with the additional advantage of helping the automated proof search procedures by reducing the size and complexity of the premises and by instantiating and reusing once-proved properties in a variety of contexts. Filliâtre and Paskevich wrote a paper 19 demonstrating the modularity features of WhyML, the language of the program verification tool Why3. Instead of separating abstract interfaces and fully elaborated implementations, WhyML uses a single concept of module, a collection of abstract and concrete declarations, and a basic operation of cloning which instantiates a module with respect to a given partial substitution, while verifying its soundness. This mechanism brings into WhyML both abstraction and genericity, which is illustrated on a small verified Bloom filter implementation, translated into executable idiomatic C code.
- Continuation Passing as an Abstract Syntax for Deductive Verification A. Paskevich proposed a continuation passing style to devise an extremely economical abstract syntax for a generic algorithmic language 31. This syntax is flexible enough to naturally express conditionals,loops, (higher-order) function calls, and exception handling. It is type-agnostic and state-agnostic, which means that it can be combined with a wide range of type and effect systems. It is argued that this syntax is also well suited for the purposes of deductive verification. Indeed, that work shows how this syntax can be augmented in a natural way with specification annotations, ghost code, and side-effect discipline. Rules of verification condition generation are defined for this syntax, and it appears that the resulting formulas are nearly identical to what traditional approaches, like the weakest precondition calculus, produce for the equivalent algorithmic constructions. This constitutes a minimalistic yet versatile abstract syntax for annotated programs for which one can compute verification conditions without sacrificing their size, legibility, and amenability to automated proof, compared to more traditional methods. We believe that it makes it an excellent candidate for internal code representation in program verification tools.
7.2 Reasoning on mutable memory in program verification
-
Ghost Monitors
M. Clochard, C. Marché and A. Paskevich proposed a new approach to deductive program verification based on auxiliary programs called ghost monitors. This technique is useful when the syntactic structure of the target program is not well suited for verification, for example, when an essentially recursive algorithm is implemented in an iterative fashion. This new approach consists in implementing, specifying, and verifying an auxiliary program that monitors the execution of the target program, in such a way that the correctness of the monitor entails the correctness of the target. The ghost monitor maintains the necessary data and invariants to facilitate the proof. It can be implemented and verified in any suitable framework, which does not have to be related to the language of the target programs. This technique is also applicable when one wants to establish relational properties between two target programs written in different languages and having different syntactic structure.
Ghost monitors can be used to specify and prove fine-grained properties about the infinite behaviors of target programs. Since this cannot be easily done using existing verification frameworks, this work introduces a dedicated language for ghost monitors, with an original construction to catch and handle divergent executions. The soundness of the underlying program logic is established using a particular flavor of transfinite games. This language and its soundness are formalized and mechanically checked. 17
- Deductive program verification for a language with a Rust-like typing discipline When verifying programs using a mutable heap, it is often required to show that pointers do not alias each other, ensuring there is only one way to modify structures in memory. This leads to cumbersome proof obligations and makes verification much more challenging. Newer languages like Rust feature pointers as well but prevent aliasing through the type system. This opens the door to simpler approaches to verification, free of tedious proof obligations. In his master thesis, X. Denis proposed a technique for the verification of Rust programs by translation to a functional language. The challenge of this translation is the handling of mutable borrows: pointers which control of aliasing in a region of memory. To overcome this, he used a technique inspired by prophecy variables to predict the final values of borrows. 30
- Verification of Programs with Pointers in SPARK G.-A. Jaloyan (CEA), C. Dross (AdaCore), M. Maalej (AdaCore), Y. Moy (AdaCore) et A. Paskevich introduced pointers to SPARK, a well-defined subset of the Ada language, intended for formal verification 20. In this work, the alias safety is ensured by a permission-based static alias analysis method inspired by Rust's borrow-checker and affine types. This extension has been implemented in the SPARK GNATprove formal verification toolset for Ada.
- Parameterized Model Checking on the TSO Weak Memory Model Modern multiprocessors and microprocessors implement weak or relaxed memory models, in which the apparent order of memory operation does not follow the sequential consistency (SC) proposed by Leslie Lamport. Any concurrent program running on such architecture and designed with an SC model in mind may exhibit new behaviors during its execution, some of which may potentially be incorrect. For instance, a mutual exclusion algorithm, correct under an interleaving semantics, may no longer guarantee mutual exclusion when implemented on a weaker architecture. Reasoning about the semantics of such programs is a difficult task. Moreover, most concurrent algorithms are designed for an arbitrary number of processes. D. Declerck, S. Conchon and F. Zaïdi proposed an approach to ensure the correctness of such concurrent algorithms, regardless of the number of processes involved. It relies on the Model Checking Modulo Theories framework, developed by Ghilardi and Ranise, which allows for the verification of safety properties of parameterized concurrent programs, that is to say, programs involving an arbitrary number of processes. This technology is extended with a theory for reasoning about weak memory models. The result is an extension of the Cubicle model checker called Cubicle-W, which allows the verification of safety properties of parameterized transition systems running under a weak memory model similar to TSO. 12
7.3 Verification of Computer Arithmetic
- WhyMP, a Formally Verified Arbitrary-Precision Integer Library The WhyMP library implements some algorithms of the GNU Multi-Precision library (GMP), the state-of-the-art C library for performing computations on arbitrary-precision integers. WhyMP is written in WhyML, the programming language offered by the Why3 software verification framework, and the functional correctness of the algorithms is formally verified. The WhyML code is then extracted as a C library that is binary-compatible with GMP and can be substituted to it in existing programs. Performance-wise, it is competitive with the no-assembly version of GMP, for small and medium-sized inputs 2127.
-
Optimal Inverse Projection of Floating-Point Addition
In a setting where we have intervals for the values of
floating-point variables
- Emulating round-to-nearest-ties-to-zero "augmented" floating- point operations The 2019 version of the IEEE 754 Standard for Floating-Point Arithmetic recommends that new “augmented” operations should be provided for the binary formats. These operations use a new “rounding direction”: round to nearest ties-to-zero. S. Boldo, C. Lauter, and J.-M. Muller show how they can be implemented using the currently available operations, using round-to-nearest ties-to-even with a partial formal proof of correctness 11.
- A Correctly-Rounded Fixed-Point-Arithmetic Dot-Product Algorithm Dot products are ubiquitous in matrix computations, for instance in signal processing. We are especially interested in digital filters, where they are the core operation. We therefore focus on fixed-point arithmetic, used in embedded systems for time and energy efficiency. Common dot product algorithms ensure faithful rounding. For the sake of accuracy and reproducibility, we want to ensure correct rounding. We developed an algorithm that computes a correctly-rounded sum of products from inputs whose format is known in advance 16
7.4 Spreading Formal Proofs
-
Formal Analysis of Debian packages
Several new results were produced in the context of the CoLiS project for the formal analysis of Debian packages. A first important step is the version 2 of the design of the CoLiS language done by B. Becker, C. Marché and other co-authors 38, that includes a modified formal syntax, a extended formal semantics, together with the design of concrete and symbolic interpreters. Those interpreters are specified and implemented in Why3, proved correct (following the initial approach for the concrete interpreter published in 2018 52 and the recent approach for symbolic interpretation mentioned above 37), and finally extracted to OCaml code.
To make the extracted code effective, it must be linked together with a library that implements a solver for feature constraints 54, and also a library that formally specifies the behavior of basic UNIX utilities. The latter library is documented in details in a research report 53.
A third result is a large verification campaign running the CoLiS toolbox on all the packages of the current Debian distribution. The results of this campaign were reported in another article 15 that was presented at TACAS conference in 2020. The most visible side effect of this experiment is the discovery of bugs: more than 150 bugs report have been filled against various Debian packages.
- Functional Programming. At JFLA 2020, J.-C. Filliâtre gave a talk related to the elimination of non-tail calls 22. The example taken is that of a small recursive function to compute the height of a binary tree. Several solutions to avoid a stack overflow are given, compared, and discussed according to the programming language.
- A Coq retrospective — at the heart of Coq architecture, the genesis of version 7.0 During Fall 1999, J.-C. Filliâtre designed and implemented a new architecture for the Coq proof assistant, to isolate a “kernel of trust”. This architecture is still in use today. In June 2020, J.-C. Filliâtre was invited speaker at the Coq Workshop 24 to give an account on that work.
- Formal Verification of “ParcourSup” algorithms. A first part of this work was the verification of the first algorithm of Parcoursup using Why3. Most of the expected properties, taken from the public description of Parcoursup's algorithms, have been verified 33. We then worked on the verification of the Java source code of ParcourSup. The findings and lessons learnt are described in a report 29.
-
An Early-Stage Prototype of a Key Server Developed using
Why3
In the context of the VerifyThis Collaborative Long Term
Challenge 2020 (https://
verifythis. ), we used the Why3 verification framework to design, from scratch, a simple but running prototype implementation of a PGP key server. We exploit the ability of Why3 to extract OCaml code from verified WhyML code so as to produce code that can be compiled into an executable. Our prototype is made of a combination of unverified handwritten OCaml code and of WhyML code whose functional behaviour is formally specified and proven correct 18.github. io/
8 Bilateral contracts and grants with industry
We have bilateral contracts which are closely related to a joint effort called the ProofInUse joint Laboratory. The objective of ProofInUse is to provide verification tools, based on mathematical proof, to industry users. These tools are aimed at replacing or complementing the existing test activities, whilst reducing costs.
This joint laboratory is a follow-up of the former “LabCom
ProofInUse” between Toccata and the SME AdaCore, funded by the ANR
programme “Laboratoires communs”, from April 2014 to March 2017
http://
8.1 ProofInUse-AdaCore Collaboration
Participants: Claude Marché, Jean-Christophe Filliâtre, Andrei Paskevich, Guillaume Melquiond, Benedikt Becker.
This collaboration is a joint effort of the Inria project-team Toccata and the AdaCore company which provides development tools for the Ada programming language. It is funded by a 5-year bilateral contract from Jan 2019 to Dec 2023.
The SME AdaCore is a software publisher specializing in providing software development tools for critical systems. A previous successful collaboration between Toccata and AdaCore enabled Why3 technology to be put into the heart of the AdaCore-developed SPARK technology.
The objective of ProofInUse-AdaCore is to significantly increase the capabilities and performances of the Spark/Ada verification environment proposed by AdaCore. It aims at integration of verification techniques at the state-of-the-art of academic research, via the generic environment Why3 for deductive program verification developed by Toccata.
8.2 ProofInUse-MERCE Collaboration
Participants: Claude Marché, Guillaume Melquiond, Cláudio Belo Lourenço.
This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company Mitsubishi Electric R&D (MERCE) in Rennes. It is funded by a bilateral contract of 18 months from Nov 2019 to April 2021.
MERCE has strong and recognized skills in the field of formal methods. In the industrial context of the Mitsubishi Electric Group, MERCE has acquired knowledge of the specific needs of the development processes and meets the needs of the group in different areas of application by providing automatic verification and demonstration tools adapted to the problems encountered.
The objective of ProofInUse-MERCE is to significantly improve on-going MERCE tools regarding the verification of Programmable Logic Controllers and also regarding the verification of numerical C codes.
8.3 ProofInUse-TrustInSoft Collaboration
Participants: Claude Marché, Guillaume Melquiond.
This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company TrustInSoft in Paris. It is funded by a bilateral contract of 18 months from Dec 2020 to April 2022.
TrustInSoft is an SME that offers the TIS-Analyzer environment for
analysis of safety and security properties of source codes
written in C and C++ languages. A version of TIS-Analyzer is
available online, under the name TaaS (TrustInSoft as a
Service, https://
The objective of ProofInUse-TrustInSoft is to integrate Deductive Verification in the platform TIS-Analyzer, with a special interest in the generation of counterexample to help the user in case of proof failure.
8.4 CEA-DAM Collaboration
Participants: Sylvie Boldo, Louise Ben Salem-Knapp.
A contract will be signed in 2021 between the CEA-DAM (“Direction des applications militaires”) and Toccata about the management of the PhD thesis of Louise Ben Salem-Knapp with William Weens (CEA-DAM) and Guillaume Perrin (CEA-DAM).
This topic of the PhD is between computer science and applied mathematics. We consider algorithms from numerical analysis and verify their good behavior on computers. This behavior, proven by supposing that the computations are perfect, could be put in fault by the problems of round-off errors and of overflows due to computations in floating-point arithmetic. We plan to study the impact of round-off errors in a hydrodynamic code. Hydrodynamics is the skeleton model of many physical models used in industry. It contains numerous technical, mathematical and numerical difficulties, which does not prevent its massive use in the simulation industry on increasingly complex problems. Today, the resolution of such problems requires the use of super-calculators, as well as the implementation of algorithms adapted to massively parallel calculation. The very large number of calculations required to produce results raises the question of their numerical quality.
8.5 CIFRE contract with TrustInSoft company
Participants: Guillaume Melquiond, Raphaël Rieu-Helft.
Jointly with the thesis of R. Rieu-Helft, supervised in collaboration with the TrustInSoft company, we established a 3-year bilateral collaboration contract, that ended in November 2020. The aim is to design methods that make it possible to design an arbitrary-precision integer library that, while competitive with the state-of-the-art library GMP, is formally verified. Not only are GMP's algorithm especially intricate from an arithmetic point of view, but numerous tricks were also used to optimize them. We are using the Why3 programming language to implement the algorithms, we are developing reflection-based procedures to verify them, and we finally extract them as a C library that is binary-compatible with GMP 921. The PhD thesis has been defended in Nov. 2020 27.
9 Partnerships and cooperations
9.1 European Initiatives
9.1.1 FP7 & H2020 Projects
EMC2, ERC Synergy project
- Title: Extreme-scale Mathematically-based Computational Chemistry
- Duration: Nov 2019 - April 2026
- Coordinators: E. Cances, L. Grigori, Y. Maday, and J. P. Piquemal
-
Partners:
- LJLL and LCT, Sorbonne Université (France)
- Cermics, ECOLE NATIONALE DES PONTS ET CHAUSSEES (France)
- Inria contact: Laura Grigori
-
Summary:
EMC2 is an ERC Synergy project that aims to overcome some of the current limitations in the field of molecular simulation and aims to provide academic communities and industrial companies with new generation, dramatically faster and quantitatively reliable molecular simulation software. This will enable those communities to address major technological and societal challenges of the 21st century in health, energy and the environment for instance.
9.1.2 Collaborations in European Programs, except FP7 and H2020
- Program: COST (European Cooperation in Science and Technology).
- Project acronym: EUTypes https://
eutypes. cs. ru. nl/ - Project title: The European research network on types for programming and verification
- Duration: 2015-2019
- Coordinator: Herman Geuvers, Radboud University Nijmegen, The Netherlands
- Other partners: 36 members countries, see http://
www. cost. eu/ COST_Actions/ ca/ CA15123?parties -
Abstract: Types are pervasive in programming and information technology. A type defines a formal interface between software components, allowing the automatic verification of their connections, and greatly enhancing the robustness and reliability of computations and communications. In rich dependent type theories, the full functional specification of a program can be expressed as a type. Type systems have rapidly evolved over the past years, becoming more sophisticated, capturing new aspects of the behaviour of programs and the dynamics of their execution.
This COST Action will give a strong impetus to research on type theory and its many applications in computer science, by promoting (1) the synergy between theoretical computer scientists, logicians and mathematicians to develop new foundations for type theory, for example as based on the recent development of "homotopy type theory”, (2) the joint development of type theoretic tools as proof assistants and integrated programming environments, (3) the study of dependent types for programming and its deployment in software development, (4) the study of dependent types for verification and its deployment in software analysis and verification. The action will also tie together these different areas and promote cross-fertilisation.
9.2 National Initiatives
9.2.1 ANR CoLiS
Participants: Claude Marché, Andrei Paskevich.
The CoLiS research project is funded by the programme “Société de
l'information et de la communication” of the ANR, for a period of
60 months, starting on October 1st,
2015. http://
The project aims at developing formal analysis and verification techniques and tools for scripts. These scripts are written in the POSIX or bash shell language. Our objective is to produce, at the end of the project, formal methods and tools allowing to analyze, test, and validate scripts. For this, the project will develop techniques and tools based on deductive verification and tree transducers stemming from the domain of XML documents.
Partners: Université Paris-Diderot, IRIF laboratory (formerly PPS & LIAFA), coordinator; Inria Lille, team LINKS
9.2.2 ANR Vocal
Participants: Jean-Christophe Filliâtre, Andrei Paskevich.
The Vocal research project is funded by the programme “Société de
l'information et de la communication” of the ANR, for a period of 60
months, starting on October 1st, 2015. See https://
The goal of the Vocal project is to develop the first formally verified library of efficient general-purpose data structures and algorithms. It targets the OCaml programming language, which allows for fairly efficient code and offers a simple programming model that eases reasoning about programs. The library will be readily available to implementers of safety-critical OCaml programs, such as Coq, Astrée, or Frama-C. It will provide the essential building blocks needed to significantly decrease the cost of developing safe software. The project intends to combine the strengths of three verification tools, namely Coq, Why3, and CFML. It will use Coq to obtain a common mathematical foundation for program specifications, as well as to verify purely functional components. It will use Why3 to verify a broad range of imperative programs with a high degree of proof automation. Finally, it will use CFML for formal reasoning about effectful higher-order functions and data structures making use of pointers and sharing.
Partners: team Gallium (Inria Paris-Rocquencourt), team DCS (Verimag), TrustInSoft, and OCamlPro.
9.2.3 FUI LCHIP
Participants: Sylvain Conchon.
LCHIP (Low Cost High Integrity Platform) is aimed at easing the
development of safety critical applications (up to SIL4) by
providing: (i) a complete IDE able to automatically generate and
prove bounded complexity software (ii) a low cost, safe execution
platform. The full support of DSLs and third party code generators
will enable a seamless deployment into existing development cycles.
LCHIP gathers scientific results obtained during the last 20 years
in formal methods, proof, refinement, code generation, etc. as well
as a unique return of experience on safety critical systems design.
http://
Partners: 2 technology providers (ClearSy, OcamlPro), in charge of building the architecture of the platform; 3 labs (IFSTTAR, LIP6, LRI), to improve LCHIP IDE features; 2 large companies (SNCF, RATP), representing public ordering parties, to check compliance with standard and industrial railway use-case.
The project led by ClearSy has started in April 2016 and lasts 3 years. It is funded by BpiFrance as well as French regions.
9.2.4 ANR PARDI
Participants: Sylvain Conchon.
Verification of PARameterized DIstributed systems. A parameterized
system specification is a specification for a whole class of
systems, parameterized by the number of entities and the properties
of the interaction, such as the communication model
(synchronous/asynchronous, order of delivery of message, application
ordering) or the fault model (crash failure, message loss). To
assist and automate verification without parameter instantiation,
PARDI uses two complementary approaches. First, a fully automatic
model checker modulo theories is considered. Then, to go beyond the
intrinsic limits of parameterized model checking, the project
advocates a collaborative approach between proof assistant and model
checker. http://
The project led by Toulouse INP/IRIT started in 2016 and lasts for 4 years. Partners: Université Pierre et Marie Curie (LIP6), Université Paris-Sud (LRI), Inria Nancy (team VERIDIS)
9.2.5 ANR NuSCAP
Participants: Guillaume Melquiond, Sylvie Boldo.
The last twenty years have seen the advent of computer-aided proofs in
mathematics and this trend is getting more and more important. They
request various levels of numerical safety, from fast and stable
computations to formal proofs of the computations. Hovewer, the
necessary tools and routines are usually ad hoc, sometimes
unavailable, or inexistent. On a complementary perspective, numerical
safety is also critical for complex guidance and control algorithms,
in the context of increased satellite autonomy. We plan to design a
whole set of theorems, algorithms and software developments, that will
allow one to study a computational problem on all (or any) of the
desired levels of numerical rigor. Key developments include fast and
certified spectral methods and polynomial arithmetic, with subsequent
formal verifications. There will be a strong feedback between the
development of our tools and the applications that motivate it.
https://
The project led by École Normale Supérieure de Lyon (LIP) has started in February 2021 and lasts for 4 years. Partners: Inria (teams Aric, Galinette, Lfant, Marelle, Toccata), École Polytechnique (LIX), Sorbonne Université (LIP6), Université Sorbonne Paris Nord (LIPN), CNRS (LAAS).
10 Dissemination
10.1 Promoting Scientific Activities
10.1.1 Scientific Events: Selection
Chair of Conference Program Committees
- A. Paskevich, 6th Workshop on Formal Integrated Development Environment, F-IDE'2021
Member of the Conference Program Committees
- S. Boldo, 27th IEEE Symposium on Computer Arithmetic, ARITH'2020
- S. Boldo, 13th International Workshop on Numerical Software Verification, NSV'2021
- S. Boldo, Coq Workshop 2020
- S. Boldo, 28th IEEE Symposium on Computer Arithmetic, ARITH'2021
- S. Boldo, 13th NASA Formal Methods Symposium, NFM'2021
- J.-C. Filliâtre, Symposium on Languages, Applications and Technologies, SLATE 2020
- J.-C. Filliâtre, Verified Software: Theories, Tools, and Experiments, VSTTE 2020
- J.-C. Filliâtre, 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2020
- J.-C. Filliâtre, Verification, Model Checking, and Abstract Interpretation, VMCAI 2021
- J.-C. Filliâtre, 13th NASA Formal Methods Symposium, NFM'2021
- J.-C. Filliâtre, XXV Brazilian Symposium on Programming Languages, SBLP 2021
- J.-C. Filliâtre, Symposium on Languages, Applications and Technologies, SLATE 2021
- G. Melquiond, 27th IEEE Symposium on Computer Arithmetic, ARITH'2020
- G. Melquiond, 28th IEEE Symposium on Computer Arithmetic, ARITH'2021
Reviewer
In 2020, the members of the Toccata team reviewed numerous papers for numerous international conferences. Here is a non-exhaustive list.
- C. Marché: TACAS 2021
- G. Melquiond: ARITH 2020, CPP 2020, ISSAC 2020
- A. Paskevich: VMCAI 2021
10.1.2 Journal
Member of the Editorial Boards
- J.-C. Filliâtre, member of the editorial board of Journal of Functional Programming.
- G. Melquiond, member of the editorial board of Reliable Computing.
Reviewer - Reviewing Activities
In 2020, the members of the Toccata team reviewed numerous papers for numerous international journals. Here is a non-exhaustive list.
- J.-C. Filliâtre: Journal of Functional Programming
- C. Marché: Journal of Automated Reasoning
- G. Melquiond: ACM Transactions on Mathematical Software
- A. Paskevich: Journal of Automated Reasoning
10.1.3 Invited Talks
- S. Boldo : Formal Methods in Mathematics / Lean Together 2020, January 6th–10th, Carnegie Mellon University, in Pittsburgh, Pennsylvania.
- S. Boldo : CMAP, Palaiseau on Feb 4th.
- J.-C. Filliâtre : A Coq retrospective — at the heart of Coq architecture, the genesis of version 7.0 / The Coq Workshop 2020.
10.1.4 Leadership within the Scientific Community
- S. Boldo, elected chair of the ARITH working group of the GDR-IM (a CNRS subgroup of computer science) with L.-S. Didier (Univ. Toulon).
- S. Boldo, steering committee member of the IEEE International Symposium on Computer Arithmetic.
- J.-C. Filliâtre, chair of IFIP WG 1.9/2.15 verified Software.
10.1.5 Scientific Expertise
- S. Boldo, member of the Inria DR recruitment committee.
- S. Boldo, member of the Inria CRCN national recruitment committee.
- S. Boldo, member of a recruitment committee for a full professor position at Université de Montpellier.
- S. Boldo, member of the program committee for selecting postdocs of the maths/computer science program of the Labex mathématique Hadamard.
- S. Boldo, member of the Scientific Council of CentraleSupélec.
- S. Boldo, member of the HCERES committee for evaluating the LaBRI laboratory, Bordeaux, Jan 18th-21st 2021
- S. Boldo, member of the CDT commission of Saclay (“commission de développement technologique”).
- J.-C. Filliâtre, external reviewer for a Canadian NSERC Grant.
- J.-C. Filliâtre, grading the entrance examination at X/ENS (“option informatique”).
- J.-C. Filliâtre, member of jury for Prix de thèse 2020 du GDR GPL
- C. Marché, member of a recruitment committee for a full professor position in computer science at École Normale Supérieure de Paris-Saclay.
- G. Melquiond, member of the scientific commission of Inria Saclay, in charge of selecting candidates for PhD grants, Post-doc grants, temporary leaves from universities (“délégations”).
- G. Melquiond, elected member of the ED-STIC doctoral school from Université Paris-Saclay, in charge of selecting candidates for PhD grants and monitoring PhD students.
- G. Melquiond, member of two recruitment committees (full professor position and full assistant professor position) at École Polytechnique.
10.1.6 Research Administration
- S. Boldo, deputy scientific director (DSA) of Inria Saclay research center.
- S Boldo, member of the CLFP (“commission locale de formation permanente”).
- S. Boldo, member of the (national) Inria IES commission (”commission pour l'information et l'édition scientifique”) about scientific edition and publication models.
- S. Boldo, member of the (temporary) council of the Computer Science Graduate School of Université Paris-Saclay.
- S. Boldo, member of the CoDiReV Paris-Saclay (committee of the research heads of the Paris-Saclay components and partners).
- S. Boldo, deputy member of the CFVU Paris-Saclay (“commission de la formation et de la vie universitaire”).
- S. Boldo, member of the partners commission for the Digicosme Labex (“comité des tutelles du labex Digicosme”).
- S. Boldo, member of the crisis unit of Inria Saclay.
- G. Melquiond, member of the committee for the monitoring of PhD students (“commission de suivi doctoral”).
- A. Paskevich, member of the CCSU (“commission consultative de spécialistes de l'université”), section 27, of Université Paris-Saclay.
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- S. Boldo, Floating-point Arithmetic and Beyond, 6h, M2, École Normale Supérieure de Lyon, France.
- S. Conchon and J.-C. Filliâtre, DIU Enseigner l'Informatique au Lycée, 2 weeks, rectorat de Versailles (together with T. Balabonski and K. Nguyen).
- J.-C. Filliâtre, Langages de programmation et compilation, 25h, L3, École Normale Supérieure, France.
- J.-C. Filliâtre, Les bases de l'algorithmique et de la programmation, 15h, L3, École Polytechnique, France.
- J.-C. Filliâtre, Compilation, 18h, M1, École Polytechnique, France.
- Q. Garchery, Compilation, 24h, L3, Université Paris-Saclay, France.
- Q. Garchery, Programmation Fonctionnelle Avancée, 24h, L3, Université Paris-Saclay, France.
- Q. Garchery, Algorithmique, 10h, 2nd year, Polytech, Université Paris-Saclay, France.
- A. Lanco, Graph et Outils Logiques, 24h, L2, Université Paris-Saclay, France.
- A. Lanco, Introduction à la programmation fonctionnelle, 16h, L2, Université Paris-Saclay, France.
- A. Lanco, Programmation Fonctionnelle Avancée, 24h, L3, Université Paris-Saclay, France.
- A. Lanco, Réseaux Avancés, 24h, L3, Université Paris-Saclay, France.
- C. Marché,
https://
wikimpri. : Proofs of Programshttps://dptinfo. ens-cachan. fr/ doku. php marche. , 12h, M2, Master Parisien de Recherche en Informatique (MPRI).gitlabpages. inria. fr/ lecture-deductive-verif/ - G. Melquiond, Initiation à la recherche, 12h, M1, MPRI, École Normale Supérieure Paris-Saclay, France.
- G. Melquiond, Floating-point Arithmetic and Beyond, 9h, M2, École Normale Supérieure de Lyon, France.
- A. Paskevich, Vérification Déductive, 12h, M1, MPRI, Université Paris-Saclay, France.
- A. Paskevich, Principes de systèmes d'exploitation, 40h+54h, DUT2, IUT d'Orsay, Université Paris-Saclay, France.
10.2.2 Supervision
- PhD: R. Rieu-Helft, “Développement et vérification de bibliothèques d'arithmétique entière en précision arbitraire”, since Oct. 2017, supervised by G. Melquiond and P. Cuoq (TrustInSoft), defended in Nov. 2020 27.
- PhD in progress: D. Gallois-Wong, “Vérification formelle et filtres numériques”, since Oct. 2017, supervised by S. Boldo and T. Hilaire.
- PhD in progress: Q. Garchery, “Certification de la génération et de la transformation d’obligations de preuve”, since Oct. 2018, supervised by C. Keller, C. Marché and A. Paskevich.
- PhD in progress: A. Lanco, “Stratégies pour la réduction forte”, since Oct. 2019, supervised by T. Balabonski and G. Melquiond.
- PhD in progress: C. Pascutto, “Runtime and Deductive Verification of OCaml programs and applications to Mergeable Data Structures”, since June 2020, supervised by J.-C. Filliâtre.
- PhD in progress: L. Ben Salem-Knapp, “Erreurs d’arrondi sur un code d’hydrodynamique”, since Oct. 2020, supervised by S. Boldo, W. Weens and G. Perrin.
- PhD in progress: X. Denis, “Deductive program verification for Rust”, since Oct. 2020, supervised by J.-H. Jourdan and C. Marché.
- M2 Internship: X. Denis, “Deductive program verification for a language with a Rust-like typing discipline”, Mar.-Aug. 2020, supervised by J.-H. Jourdan and C. Marché 30.
- L3 internship: J. Moreau (Université Paris-Saclay), “Vérification formelle d’une implémentation OCaml du crible d’Euler”, Jun-Jul 2020, supervised by J.-C. Filliâtre.
- M1 Internship: C. Elya (Université Saint-Joseph de Beyrouth), “Translating WhyML to Scala”, Summer 2020, supervised by J.-C. Filliâtre.
10.2.3 Juries
- S. Boldo, president of the PhD defense of Charlie Jacomme, ENS Paris-Saclay, Oct 16th
- S. Boldo, reviewer of the habilitation of Assia Mahboubi, Université de Nantes, Jan 5th 2021
10.3 Popularization
10.3.1 Education
Together with Thibaut Balabonski and Kim Nguyen, Sylvain Conchon and Jean-Christophe Filliâtre wrote Numérique et Sciences Informatiques, 24 leçons avec exercices corrigés. Terminale26 (Ellipses, 2020). It is a second volume, the first one targeting the “classe de Première” (Ellipses, 2019).
10.3.2 Interventions
Sylvie Boldo took part of a popularization radio program about
computer science
https://
11 Scientific production
11.1 Major publications
- 1 articleLet's Verify This with Why3International Journal on Software Tools for Technology Transfer (STTT)1762015, 709--727
- 2 articleVerified Compilation of Floating-Point ComputationsJournal of Automated Reasoning542February 2015, 135-163URL: https://hal.inria.fr/hal-00862689
- 3 bookComputer Arithmetic and Formal Proofs: Verifying Floating-point Algorithms with the Coq SystemISTE Press - ElsevierDecember 2017, URL: https://hal.inria.fr/hal-01632617
- 4 articleThe Matrix ReprovedJournal of Automated Reasoning6032018, 365--383URL: https://hal.inria.fr/hal-01617437
- 5 inproceedingsA Three-tier Strategy for Reasoning about Floating-Point Numbers in SMTComputer Aided Verification2017, URL: https://hal.inria.fr/hal-01522770
- 6 articleThe Spirit of Ghost CodeFormal Methods in System Design4832016, 152--174URL: https://hal.science/hal-01396864v1
- 7 inproceedingsSpecification and Proof of High-Level Functional Properties of Bit-Level Programs8th NASA Formal Methods Symposium9690Lecture Notes in Computer ScienceMinneapolis, MN, USASpringerJune 2016, 291--306URL: https://hal.inria.fr/hal-01314876
- 8 articleProving Tight Bounds on Univariate Expressions with Elementary Functions in CoqJournal of Automated Reasoning2016, URL: https://hal.inria.fr/hal-01086460
- 9 inproceedingsA Why3 Framework for Reflection Proofs and its Application to GMP's Algorithms9th International Joint Conference on Automated ReasoningLecture Notes in Computer ScienceOxford, United KingdomJuly 2018, URL: https://hal.inria.fr/hal-01699754
- 10 inproceedingsA Non-linear Arithmetic Procedure for Control-Command Software Verification24th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS)Thessalonique, GreeceApril 2018, URL: https://hal.science/hal-01737737
11.2 Publications of the year
International journals
- 11 article Emulating round-to-nearest ties-to-zero "augmented" floating-point operations using round-to-nearest ties-to-even arithmetic IEEE Transactions on Computers 2020
- 12 articleParameterized Model Checking on the TSO Weak Memory ModelJournal of Automated Reasoning647October 2020, 1307-1330
- 13 article Simpler Proofs with Decentralized Invariants Journal of Logical and Algebraic Methods in Programming 121 June 2021
- 14 articleOptimal Inverse Projection of Floating-Point AdditionNumerical Algorithms8332020, 957--986
International peer-reviewed conferences
- 15 inproceedingsAnalysing installation scenarios of Debian packagesTools and Algorithms for the Construction and Analysis of SystemsTACAS 2020 - 26th International Conference on Tools and Algorithms for the Construction and Analysis of Systems12079Lecture Notes in Computer ScienceDublin, IrelandApril 2020, 235-253
- 16 inproceedingsA Correctly-Rounded Fixed-Point-Arithmetic Dot-Product AlgorithmARITH 2020 - IEEE 27th Symposium on Computer ArithmeticPortland, United StatesJune 2020, 9-16
- 17 inproceedings Deductive Verification with Ghost Monitors POPL 2020 - 47th ACM SIGPLAN Symposium on Principles of Programming Languages New Orleans, United States 2020
- 18 inproceedingsYou-Know-Why: an Early-Stage Prototype of a Key Server Developed using Why3VerifyThis 2020 - Long-term ChallengeDublin, IrelandJune 2020, 4--7
- 19 inproceedings Abstraction and Genericity in Why3 ISoLA 2020 - 9th International Symposium On Leveraging Applications of Formal Methods, Verification and Validation 12476 Rhodes, Greece http://isola-conference.org/isola2020/ October 2020
- 20 inproceedingsVerification of Programs with Pointers in SPARKICFEM 2020: Formal Methods and Software EngineeringSingapore, SingaporeDecember 2020, 55-72
- 21 inproceedingsWhyMP, a Formally Verified Arbitrary-Precision Integer LibraryISSAC'20: Proceedings of the 45th International Symposium on Symbolic and Algebraic ComputationISSAC 2020 - 45th International Symposium on Symbolic and Algebraic ComputationKalamata, Greecehttp://issac-conference.org/2020/July 2020, 352-359
National peer-reviewed Conferences
- 22 inproceedings Mesurer la hauteur d'un arbre JLFA 2020 - Journées Francophones des Langages Applicatifs Gruissan, France January 2020
- 23 inproceedings Des transformations logiques passent leur certicat JFLA 2020 - Journées Francophones des Langages Applicatifs Gruissan, France 2020
Conferences without proceedings
- 24 inproceedings a Coq retrospective - at the heart of Coq architecture, the genesis of version 7.0 The Coq Workshop 2020 virtual, France July 2020
- 25 inproceedings Low Cost High Integrity Platform: regular paper ERTS 2020 - 10th European Congress on Embedded Real Time Systems Toulouse, France January 2020
Scientific books
- 26 bookNumérique et Sciences Informatiques, 24 leçons avec exercices corrigés. Terminalehttps://www.editions-ellipses.fr/accueil/10445-20818-specialite-numerique-et-sciences-informatiques-lecons-avec-exercices-corriges-terminale-nouveaux-programmes-9782340038554.htmlJuly 2020, 526
Doctoral dissertations and habilitation theses
- 27 thesis Development and verification of arbitrary-precision integer arithmetic libraries Université Paris-Saclay November 2020
Reports & preprints
- 28 misc A strong call-by-need calculus February 2021
- 29 report Rapport d'avancement sur la vérification formelle des algorithmes de ParcourSup Université Paris-Saclay January 2020
- 30 report Deductive program verification for a language with a Rust-like typing discipline Université de Paris September 2020
- 31 misc Continuation Passing as an Abstract Syntax for Deductive Verification January 2021
11.3 Cited publications
- 32 book W. Ahrendt B. Beckert R. Bubel R. Hähnle P. Schmitt M. Ulbrich Deductive Software Verification - The KeY Book - From Theory to Practice 10001 Lecture Notes in Computer Science Springer December 2016
- 33 techreportVérification par preuve formelle de propriétés fonctionnelles d'algorithme de classificationUniversité Paris SudAugust 2019, URL: https://hal.inria.fr/hal-02421484
- 34 inproceedingsMulti-Prover Verification of Floating-Point ProgramsFifth International Joint Conference on Automated Reasoning6173Lecture Notes in Artificial IntelligenceEdinburgh, ScotlandSpringerJuly 2010, 127--141URL: http://hal.inria.fr/inria-00534333
- 35 inproceedingsCVC4Proceedings of the 23rd international conference on Computer aided verificationCAV'11Berlin, HeidelbergSnowbird, UTSpringer-Verlag2011, 171--177
- 36 manual ACSL: ANSI/ISO C Specification Language, version 1.4 2009
- 37 inproceedingsGhost Code in Action: Automated Verification of a Symbolic InterpreterVerified Software: Tools, Techniques and Experiments12031Lecture Notes in Computer ScienceNew York, United StatesJuly 2019, URL: https://hal.inria.fr/hal-02276257
- 38 techreportRevision 2 of CoLiS language: formal syntax, semantics, concrete and symbolic interpretersHAL Archives OuvertesOctober 2019, URL: https://hal.inria.fr/hal-02321743
- 39 inproceedingsMETEOR : A successful application of B in a large projectProceedings of FM'99: World Congress on Formal MethodsLecture Notes in Computer Science (Springer-Verlag)Springer VerlagSeptember 1999, 369--387
- 40 inproceedingsFormal Proof of a Wave Equation Resolution Scheme: the Method ErrorProceedings of the First Interactive Theorem Proving Conference6172LNCSEdinburgh, ScotlandSpringerJuly 2010, 147--162URL: http://hal.inria.fr/inria-00450789/
- 41 articleWave Equation Numerical Resolution: a Comprehensive Mechanized Proof of a C ProgramJournal of Automated Reasoning504April 2013, 423--456URL: http://hal.inria.fr/hal-00649240/en/
- 42 inproceedingsCombining Coq and Gappa for Certifying Floating-Point Programs16th Symposium on the Integration of Symbolic Computation and Mechanised Reasoning5625Lecture Notes in Artificial IntelligenceGrand Bend, CanadaSpringerJuly 2009, 59--74
- 43 articleFormal verification of numerical programs: from C annotated programs to mechanical proofsMathematics in Computer Science542011, 377--393URL: http://hal.inria.fr/hal-00777605
- 44 articleProofs of numerical programs when the compiler optimizesInnovations in Systems and Software Engineering722011, 151--160URL: http://hal.inria.fr/hal-00777639
- 45 articleAn overview of JML tools and applicationsInternational Journal on Software Tools for Technology Transfer (STTT)73June 2005, 212--232
- 46 inproceedingsGOSPEL --- Providing OCaml with a Formal Specification LanguageFM 2019 23rd International Symposium on Formal MethodsPorto, PortugalOctober 2019, URL: https://hal.inria.fr/hal-02157484
- 47 inproceedingsOpenJML: Software Verification for Java 7 using JML, OpenJDK, and EclipseProceedings 1st Workshop on Formal Integrated Development Environment149EPTCS2014, 79--92
- 48 inproceedings Alt-Ergo 2.2 SMT Workshop: International Workshop on Satisfiability Modulo Theories Oxford, United Kingdom July 2018
- 49 articleInstrumenting a Weakest Precondition Calculus for Counterexample GenerationJournal of Logical and Algebraic Methods in Programming992018, 97--113URL: https://hal.inria.fr/hal-01802488
- 50 inproceedingsAutomating the Verification of Floating-Point ProgramsVerified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/hal-01534533/
- 51 inproceedingsVeriFast: A Powerful, Sound, Predictable, Fast Verifier for C and JavaNASA Formal Methods6617Lecture Notes in Computer ScienceSpringer2011, 41--55
- 52 inproceedingsA Formally Verified Interpreter for a Shell-like Programming LanguageVerified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/
- 53 techreportSpecification of UNIX UtilitiesHAL Archives OuvertesOctober 2019, URL: https://hal.inria.fr/hal-02321691
- 54 inproceedingsDeciding the First-Order Theory of an Algebra of Feature Trees with Updates9th International Joint Conference on Automated ReasoningOxford, United KingdomJuly 2018, URL: https://hal.science/hal-01807474
- 55 articleseL4: Formal verification of an OS kernelCommunications of the ACM536June 2010, 107--115
- 56 articleA formally verified compiler back-endJournal of Automated Reasoning4342009, 363--446URL: http://hal.inria.fr/inria-00360768/en/
-
57
articleThe
Tool for Certification of /JavaCard Programs annotated in 'Journal of Logic and Algebraic Programming581--22004, 89--106 - 58 misc The Krakatoa tool for Deductive Verification of Java Programs January 2009
- 59 book Handbook of Floating-point Arithmetic (2nd edition) Birkhäuser Basel July 2018
- 60 inproceedingsHardware-Dependent Proofs of Numerical ProgramsCertified Programs and ProofsLecture Notes in Computer ScienceSpringerDecember 2011, 314--329URL: http://hal.inria.fr/hal-00772508
- 61 articleCertifying the floating-point implementation of an elementary function using GappaIEEE Transactions on Computers6022011, 242--253URL: http://hal.inria.fr/inria-00533968/en/
- 62 inbookOpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst CaseComputer Aided Verification: 27th International Conference, CAV 2015, San Francisco, CA, USA, July 18-24, 2015, Proceedings, Part ID. KroeningC. PăsăreanuChamSpringer International Publishing2015, 273--289
- 63 inproceedingsZ3, An Efficient SMT SolverTACAS4963Lecture Notes in Computer ScienceSpringer2008, 337--340

