Keywords
Computer Science and Digital Science
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.3. Discrete Modeling (multi-agent, people centered)
- A6.1.4. Multiscale modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.3. Probabilistic methods
- A6.2.4. Statistical methods
- A6.3.1. Inverse problems
Other Research Topics and Application Domains
- B1.1.2. Molecular and cellular biology
- B1.1.3. Developmental biology
- B1.1.4. Genetics and genomics
- B1.1.5. Immunology
- B1.1.6. Evolutionnary biology
- B1.1.7. Bioinformatics
- B1.1.8. Mathematical biology
- B1.1.10. Systems and synthetic biology
- B2.2.1. Cardiovascular and respiratory diseases
- B2.2.3. Cancer
- B2.2.5. Immune system diseases
- B2.2.6. Neurodegenerative diseases
1 Team members, visitors, external collaborators
Research Scientists
- Mostafa Adimy [Team leader, Inria, Senior Researcher, HDR]
- Samuel Bernard [CNRS, Researcher, HDR]
- Vincent Calvez [CNRS, Researcher, HDR]
- Olivier Gandrillon [CNRS, Senior Researcher, HDR]
- Thomas Lepoutre [Inria, Researcher, HDR]
- Vitaly Volpert [CNRS, Senior Researcher, HDR]
Faculty Members
- Thibault Espinasse [Univ Claude Bernard, Associate Professor]
- Laurent Pujo Menjouet [Univ Claude Bernard, Associate Professor, HDR]
- Leon Matar Tine [Univ Claude Bernard, Associate Professor]
Post-Doctoral Fellow
- Madge Martin [Inria]
PhD Students
- Ghada Abi Younes [Univ Claude Bernard]
- Kyriaki Dariva [Univ Claude Bernard , ATER, from Sept 2021, Univ Saint Etienne ]
- Leonard Dekens [Univ Claude Bernard]
- Mete Demircigil [École Normale Supérieure de Paris]
- Cheikh Gueye [Univ Claude Bernard]
- Alexey Koshkin [Inria]
- Paul Lemarre [Univ Claude Bernard, until May 2021]
- Elias Ventre [École Normale Supérieure de Lyon]
Interns and Apprentices
- Louis Babin [Inria, from Apr 2021 until Jul 2021]
- Hamza Faquir [Inria, from Apr 2021 until Jul 2021]
- Theo Kaprelian [Inria, from Apr 2021 until Sep 2021]
- Vincent Marty [Inria, until Jun 2021]
- Remi Tuffet [Inria, from Apr 2021 until Jul 2021]
Administrative Assistant
- Claire Sauer [Inria, Jan 2021]
External Collaborator
- Fabien Crauste [CNRS, HDR]
2 Overall objectives
2.1 Presentation
Dracula is a joint research team between INRIA, Université Claude Bernard Lyon 1 (UCBL) and CNRS (Institut Camille-Jordan (ICJ, UMR 5208) and Laboratoire de Biologie et Modélisation de la Cellule (LBMC, UMR 5239)).
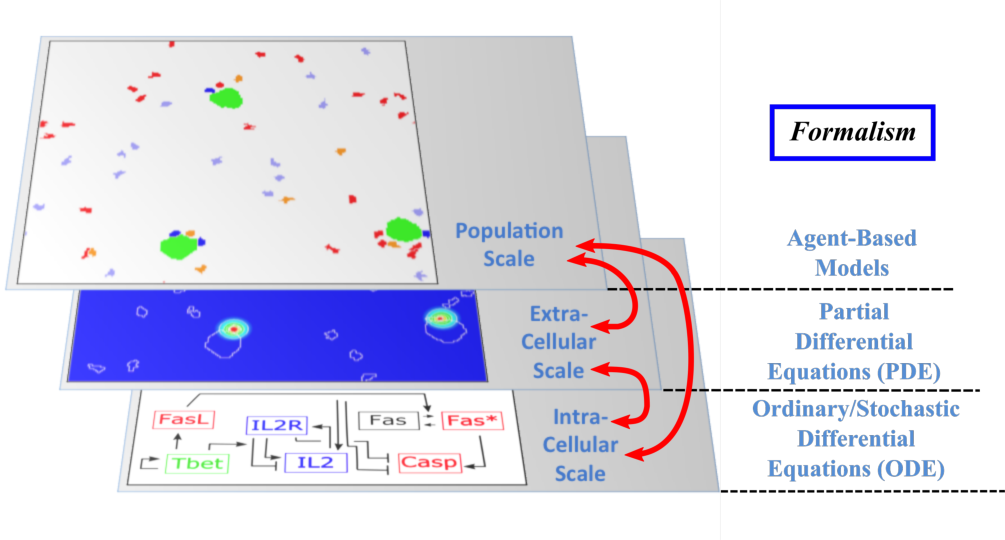
The Dracula project is devoted to multi-scale modeling in biology and medicine, and more specifically to the development of tools and methods to describe multi-scale processes in biology and medicine. Applications include normal and pathological hematopoiesis (for example leukemia), immune response, and other biological processes, like: tissue renewal, morphogenesis, atherosclerosis, prion disease, hormonal regulation of food intake, and so on. Multi-scale modeling implies simultaneous modeling of several levels of descriptions of biological processes: intra-cellular networks (molecular level), cell behavior (cellular level), dynamics of cell populations (organ or tissue) with the control by other organs (organism) (see Figure 1). Such modeling represents one of the major challenges in modern science due to its importance and because of the complexity of biological phenomena and of the presence of very different interconnected scales.
Although multi-scale modeling holds a great potential for biology and medicine, and despite the fact that a variety of techniques exists to deal with such problems, the complexity of the systems poses new challenges and needs the development of new tools. Moreover, different biological questions usually require different types of multi-scale modeling. The expected results of these studies are numerous. On one hand, they will shed new light on the understanding of specific biological and medical questions (for instance, what is the behavior of hematopoietic stem cells under pathological conditions? Or how to efficiently stimulate an immune response in order to design new vaccines?). On the other hand, the modeling methods developed here for specific processes are relevant to study other complex biological systems. We pay a special attention on developing methods that are not restricted to one or two applications.
An important part of our researches is performed in close collaboration with biologists and physicians in order to stay in contact with the biological and medical goals. The presence, within the project, of a biologist (Olivier Gandrillon) who has acquired over the years the know-how required for interacting with mathematicians is probably one of the main assets of the project. He participates actively in many tasks of our program, stimulates interactions between members of the project and biologists, and everyone benefits from his expertise in molecular and cell biology.
2.2 Keywords
Multi-scale modeling; Hybrid modeling; Mathematical Biology; Computational Biology; Immune response modeling; Normal and pathological hematopoiesis; Multi-scale cancer modeling; Regulatory networks; Reaction-diffusion equation; Structured partial differential equations; Delay differential equations; Agent-based modeling; Dynamical systems.
2.3 Research axis 1: Mathematical modeling for cell population dynamics
Executive summary
Stem cells are essential for development and keep the maintenance of many tissues homeostasis. They are characterized by their ability to self-renew as well as to produce differentiated cells. They vary enormously, for each organ, in their proliferation capacity, their potency to produce different cell lineage and their response to various environmental cues. How a cell will react to a given external signal does not depend only on its current state but also on its environment. Understanding the effect of cell-to-cell heterogeneity and the spatial organization of cell populations is therefore necessary to help keeping the normal function of an organ.
We develop mathematical tools and methods to study cell population dynamics and other biological processes: stability of steady sates, existence of bifurcations, kinetic properties, spatial organization, in finely detailed cell populations. The main tools we use are hybrid discrete-continuous models, reaction-diffusion equations, structured models (in which the population is endowed with relevant structures or traits), delay differential systems, agent-based models. Our team has acquired an international expertise in the fields of analysis of reaction-diffusion and structured equations, particularly integro-differential and delay differential equations.
The mathematical methods we develop are not restricted to hematopoietic system (Research axis 2), and immune response (Research axis 3), rather we apply them in many other biological phenomena, for example: tissue renewal, morphogenesis, prion disease, atherosclerosis, hormonal regulation of food intake, cancer, and others.
Project-team positioning
The focus of this objective is the development, analysis and application of hybrid discrete-continuous, reaction-diffusion and structured partial differential models. The structured equations allow a fine description of a population as some structures (age, maturity, intracellular content) change with time. In many cases, structured equations can be partially integrated to yield integro-differential equations (ordinary or partial differential equations involving non-local integral terms), time-delay differential or time-delay partial differential, or coupled differential-difference models. Analysis of integro-differential and time-delay systems deals with existence of solutions and their stability. Applications are found in the study of normal and pathological hematopoietic system (Research axis 2), immune response (Research axis 3), morphogenesis, prion disease, cancer development and treatment, and generally in tissue renewal problems. Models based on structured equations are especially useful to take into account the effect of finite time cells take to divide, die or become mature. Reaction-diffusion equations are used in order to describe spatial distribution of cell populations. It is a well developed area of research in our team which includes qualitative properties of travelling waves for reaction-diffusion systems with or without delay, and complex nonlinear dynamics.
Our team has developed a solid expertise in mathematical analysis of reaction-diffusion with or without delay and structured equations (in particular, delay differential equations) and one of the most prolific. Other major groups are the teams of Benoit Perthame (Pierre et Marie CURIE University and Mamba, Paris), Emmanuel Grenier (Ecole normale supérieure de Lyon and NUMED), Odo Diekmann (Utrecht University, The Netherlands), Avner Friedman (The Ohio State University, USA), Jianhong Wu (York University, Canada), Glenn Webb (Vanderbilt University, Nashville, USA), Philip K. Maini (University of Oxford, England), Mark Chaplain (University of St Andrews, Scotland), Nicola Bellomo (University of Turin, Italy). Most of the members of all these groups and of our team belong to the same mathematical community working on partial differential equations and dynamical systems with applications to biology and medicine.
Collaborations
- University of Toronto, Canada; Mathematical analysis and applications of reaction-diffusion equations (more than 30 joint papers).
- Institute of Problems of Mechanical Engineering, St.Petersburg, Russia; Dynamics of cell renewal (more than 10 joint papers).
- Department of Cell and Molecular Biology and Department of Forensic Medicine, Stockholm, Sweden; Dynamics of cell generation and turnover (3 joint papers).
- Universities of Tlemcen (Algeria) and Marrakech (Morocco); Delay differential equations (7 joint papers)
2.4 Research axis 2: Multi-scale modeling of hematopoiesis and leukemia
Executive summary
Hematopoiesis is a complex process that begins with hematopoietic stem cells (HSCs) and results in formation of mature cells: red blood cells, white cells and platelets. Blood cells are produced in the bone marrow, from where mature cells are released into the blood stream. Hematopoiesis is based on a balance between cell proliferation (including self-renewal), differentiation and apoptosis. The choice between these three possibilities is determined by intra-cellular regulatory networks and by numerous control mechanisms in the bone marrow or carried out by other organs. Intra-cellular regulatory networks are complex biochemical reactions involving proteins, enzymes and signalling molecules. The deregulation of hematopoiesis can result in numerous blood diseases including leukemia (a cancer of blood cells). One important type of leukemia is Chronic Myeloid Leukemia (CML). The strong tyrosine kinase activity of the BCR-ABL protein is the basis for the main cell effects that are observed in CML: significant proliferation, anti-apoptotic effect, disruption of stroma adhesion properties. This explains the presence in CML blood of a very important number of cells belonging to the myeloid lineage, at all stages of maturation.
Multi-scale modeling in hematopoiesis holds a great potential. A variety of techniques exists to deal with this problem. However, the complexity of the system poses new difficulties and leads to the development of new tools. The expected results of this study are numerous. On one hand, it will shed new light on the different physiological mechanisms that converge toward the continuous regeneration of blood cells, for example: the understanding of deregulation of erythropoiesis (the process of red blood cell production) under drug treatments (this can lead to lack of red blood cells (anemia), or a surplus of red blood cells), the dynamic of leukemic cells under the action of drugs and the control of their resistance to these treatments.
Project team positioning
Multi-scale modeling of hematopoiesis is one of the key points of the project that has started in the early stage of the Dracula team. Investigated by all the team members, it took many years of close discussion with biologists to get the best understanding of the key role played by the most important molecules, hormones, kinase cascade, cell communication up to the latest knowledge. One of the important questions here is to identify particular biological mechanisms (intracellular regulation, control mechanisms) and to integrate them in the different models. Our main work consisted in the development of a hybrid (continuous/discrete) model for red blood cell progenitor proliferation, survival/death, differentiation, and migration. Cells are modeled as discrete objects, and the extracellular medium is described by continuous equations for extracellular concentrations. This is to our knowledge the most complete model for erythropoiesis to date, and the only one using a multi-scale formalism. Other models published by our group and others for hematopoiesis are population-based models, mostly population structured equations (transport partial differential equations or delay differential equations). The interest in modeling hematopoiesis dates back to the 70's and two groups have been responsible for most of development in the past 40 years: Markus Loeffer's team in Leipzig, Germany (Wichmann et al. 1976, in Mathematical Models in Medicine) and Michael Mackey's team at McGill University, Montreal, Canada (Mackey 1978, Blood). Our model differs from population based models in that the regulation is directly modeled at the molecular level (See Figure 1) rather than acting on rates at the population level. Thus we can take into account non-predictable effects of interactions between different molecular pathways and between cells that would otherwise be lost in the global population rates.
Regarding modeling leukemia, we concentrated on Chronic Myeloid Leukemia (CML) and its treatment. We considered models based on ordinary differential equations for the action of the main proteins involved in CML (as BCR-ABL protein), and of transport equations (with or without delay, physiologically structured or not) to represent healthy and leukemic cell populations, take into account many interactions between proteins (especially BCR-ABL), cells (anti-apoptotic effect, etc.). The development of models for CML allowed us to interact with Franck Nicolini in Lyon (Centre Hospitalier de Lyon) and Doron Levy (Maryland University). Different schools developed models for CML and its treatment. The three leading groups are the ones of Franziska Michor (Harvard School of public health), Ingo Roeder (Institute for Medical Informatics and Biometry, Dresden) and Michael Mackey (McGill University).
Collaborations
Members of the team have worked for several years in collaboration with biologists (François Morlé, University Lyon 1) and hematologists (Charles Dumontet, Lyon and Mark Koury, Nashville) on the Modelling of normal and pathological hematopoiesis .
The work on modeling Leukemia is based on two major collaborations: firstly, an ongoing (since 2011) mathematical collaboration with the University of Maryland through the program Associate Teams Inria project, “Modelling Leukemia”. Secondly, an ongoing (since 2012) collaboration with a clinician from Hospices Civils de Lyon (Dr. F.E. Nicolini). In this framework, we shall have soon access to the data of the clinical trial PETALs ( patients).
2.5 Research axis 3: Multi-scale modeling of the immune response
Executive summary
Vaccination represents a worldwide health, social and economical challenge as it has allowed the eradication or the strong containment of several devastating diseases over the past century. However to date, most of the effective vaccines rely on the generation of neutralizing antibody responses and such vaccines have proven largely unsuccessful in the prevention against some pathogens, such as HIV or malaria. In such cases, vaccines geared towards the generation of CD8 T cell immunity may provide a better protection. The generation of memory CD8 T cells following antigenic immunization is a long process (lasting up to month in murine preclinical models), therefore strongly slowing the process of vaccine monitoring in preclinical studies. Thus, the dynamical modeling of the CD8 T cell immune response both at the cellular and molecular levels should provide an important tool to better understand the dynamics of the response and to speed-up the process and reduce costs of vaccine development.
However, currently published cellular models of the immune response are either over-simplified, not predicting important parameters of this response, or too complicated for most of their parameters to be accessible for experimental measurements, thus impeding their biological validation. Dynamical models of the CD8 T cell response at the molecular level are very scarce and there is no multi-scale model of the immune response giving insights into both the regulation at the molecular scale and the consequences on cell population dynamics.
The objective of this research axis is therefore to develop a predictive multi-scale model of the CD8 T cell response, by confronting the model at different stages to in vivo-acquired experimental data, in order to be able to investigate the influence of early molecular events on cell population dynamics few days or weeks later.
Project-team positioning
We are aiming at building and analyzing a multi-scale model of the CD8 T cell immune response, from the molecular to the cellular and potentially organismal scale. This consists in describing the dynamics at each scale with relevant formalisms as well as the careful description of the couplings between scales.
Only few research groups are actually working on the CD8 T cell immune response around the world, and none of them deals with multi-scale modeling of this response. A network developed around Alan Perelson's work in theoretical immunology in the last decades, at Los Alamos National Laboratory, and involves mainly people in various US universities or institutes. In Europe, Rob De Boer's group of theoretical immunology in Utrecht, Netherlands, is the historical leader in the CD8 T cell dynamics modeling. We considered the models developed in these groups when we started our project, and we contributed to improve them by using nonlinearities accounting for cell population interactions to regulate the response. Also, our initial focus was on the generation of memory cells associated with vaccine development so we modeled CD8 T cell responses against influenza and vaccinia viruses, whereas other groups usually consider LCMV in its chronic form.
Ron Germain's group at the NIH, and Grégoire Altan-Bonnet in subsequent works, focused on the molecular regulation of the CD4 and CD8 T cell immune responses. In particular, they built the Simmune software, which allows the modeling and simulation of molecular interactions. This software is not really devoted to multi-scale modeling yet it provides an interesting tool to describe molecular interactions. Since our aim is to couple molecular and cellular scales at the tissue level, and we do not want to consider large networks but rather small-simplified informative interaction networks, we are confident that our approach is complementary of these works.
Within Inria project-teams, NUMED develops multi-scale approaches for biological problems, and MAMBA and MONC mention models of cancer progression and treatment including immune responses. In the first case the methodology is similar, and collaborations between NUMED and DRACULA already exist (both teams are located in Lyon), but applications differ. In the second case, MAMBA and MONC are mainly focused on cancer modeling and up to now are motivated by including an action of the immune system in the fight against cancer, which is very different from what we are developing. However, both modeling approaches are complementary and could lead to interactions, in particular in the light of recent advances in medical research pointing towards an important role - and high expectations - of the immune reaction in fighting cancers. Finally, SISTM also focuses on the modeling of the immune response, mainly against HIV, but the motivation is very similar to ours: the objective is to provide tools and methods in order to efficiently develop vaccines. They consider the CD4 T cell response instead of the CD8 T cell response, and biostatistics to achieve their goals instead of multi-scale models, yet even though there is no interaction between SISTM and DRACULA at this moment our methods and objectives are close enough to foreshadow future collaborations.
Collaborations
On this topic our main collaborators are members of Jacqueline Marvel's team in Lyon in the CIRI (Centre International de Recherche en Infectiologie INSERM U1111): Dr. Jacqueline Marvel, head of the team, Dr. Christophe Arpin (CR CNRS), and other technicians and engineers of the team. They are all immunologists, specialists of the CD8 T cell response and of the generation of memory CD8 T cells.
We also interact with private companies: AltraBio, that provides tools for data analysis, and CosmoTech, that develops a modeling and simulating platform that should allow transferring our model on an easy-to-use platform devoted to commercial uses.
2.6 Evolution of research direction during the last evaluation
Reminder of the objectives given for the last evaluation
The aim of this project is the development of modern tools for multi-scale modeling in biological phenomena. During the period 2014-2017, the objectives we had fixed were to develop modern tools for multi-scale modeling of biological phenomena, as detailed hereafter:
- Multi-scale modeling of erythropoiesis, the process of red blood cell production, in order to describe normal, stress, and pathological erythropoiesis, using mathematical and computational models. This led to:
- Multi-scale modeling of the CD8 T cell immune response, in order to develop a predictive model of the CD8 T cell response, by confronting the model at different stages to in vivo-acquired experimental data;
- Population dynamics modeling, with the aim to develop general mathematical tools to study them. The main tools we were using were structured equations, in which the cell population is endowed with relevant structures, or traits. We identified limitations in using these formalisms, this is why we started developing multi-scale approaches;
- Modeling of Chronic Myeloid Leukemia (CML) treatment, using ordinary differential equations models. Our team had already developed a first model of mutant leukemic cells being resistant to chemotherapy. A next step would be to identify the parameters using experimental data;
- Multi-scale modeling carried out on the basis of hybrid discrete-continuous models, where dissipative particle dynamics (DPD) are used in order to describe individual cells and relatively small cell populations, partial differential equations (PDE) are used to describe concentrations of bio-chemical substances in the extracellular matrix, and ordinary differential equations for intracellular regulatory networks (Figure 1). An emphasis would be made on developing codes that are both flexible and powerful enough to implement variants of the model, perform simulations, produce desired outputs, and provide tools for analysis; to do so:
- We planned to contribute to a recent project named chronos, whose code (written in C++) represents heterogeneous populations of individual cells evolving in time and interacting physically and biochemically, and the objective is to make the code flexible enough to implement different formalisms within the same model, so that different components of the model can be represented in the most appropriate way;
- Partial differential equations (PDE) analysis, with a focus on reaction-diffusion equations, transport equations (hyperbolic PDEs) in which the structure can be age, maturity, protein concentration, etc., with particular cases where transport equations are reduced to delay differential equations (DDE).
Comments on these objectives over the evaluation period
We have had strong contributions to objectives 1, 2, 3, 4, and consequently to objective 5, as well as to objective 7, as mentioned in previous sections. These contributions represented the core of the team's research activity over the evaluation period, as stressed by our publications. It is however noticeable that multi-scale modeling of the immune response and of pathological hematopoiesis (leukemia) has come to represent a proportionally more important part of our activity.
Objective 6 has been pursued, the project chronos evolved to a better defined project SiMuScale that is currently being developed and aims at structuring the team's activity and providing a simulation platform that could be adapted to various biological questions necessitating multi-scale modeling.
Objectives for the next four years
The main objectives for the next four years are to continue to improve the 3 previous points: 1) Mathematical and computational modeling for cell population dynamics; 2) Multi-scale modeling of hematopoiesis and leukemia; 3) Multi-scale modeling of the immune response. In addition, we will pursue our effort to develop a simulation platform for multi-scale models (SiMuScale) and we intend to develop the use of mixed effect models and other statistical approaches to deal with the challenges offered by modern biology, in particular the generation of single cell data.
3 Research program
3.1 Mixed-effect models and statistical approaches
Most of biological and medical data that our team has to deal with consist in time series of experimental measurements (cell counts, gene expression level, etc.). The intrinsic variability of any biological system complicates its confrontation to models. The trivial use of means, eliminating the data variance, is but a second-best solution. Furthermore, the amount of data that can be experimentally generated often limits the use of classical mathematical approaches because model’s identifiability or parameter identifiability cannot be obtained. In order to overcome this issue and to efficiently take advantage of existing and available data, we plan to use mixed effect models for various applications (for instance: leukemia treatment modeling, immune response modeling). Such models were initially developed to account for individual behaviors within a population by characterizing distributions of parameter values instead of a unique parameter value. We plan to use those approaches both within that frame (for example, taking into account longitudinal studies on different patients, or different mice) but also to extend its validity in a different context: we will consider different ex vivo experiments as being “different individuals”: this will allow us to make the most of the experience-to-experience variations.
Such approaches need expertise in statistics to be correctly implemented, and we will rely on the presence of Céline Vial in the team to do so. Céline Vial is an expert in applied statistics and her experience already motivated the use of better statistical methods in various research themes. The increasing use of single cell technologies in biology make such approaches necessary and it is going to be critical for the project to acquire such skills.
3.2 Development of a simulation platform
We have put some effort in developing the SiMuScale platform, a software coded in dedicated to exploring multiscale population models, since 2014. In order to answer the challenges of multi-scale modeling it is necessary to possess an all-purpose, fast and flexible modeling tool, and SiMuScale is the choice we made. Since it is based on a core containing the simulator, and on plug-ins that contain the biological specifications of each cell, this software will make it easier for members of the team – and potentially other modelers – to focus on the model and to capitalize on existing models, which all share the same framework and are compatible with each other. Within the next four years, SiMuScale should be widely accessible and daily used in the team for multi-scale modeling. It will be developed into a real-case context, the modeling of the hematopoietic stem cell niche, in collaboration with clinicians (Eric Solary, INSERM) and physicists (Bertrand Laforge, UPMC).
3.3 Mathematical and computational modeling
Multi-scale modeling of hematopoiesis is one of the key points of the project that has started in the early stage of the Dracula team. Investigated by the team members, it took many years of close discussion with biologists to get the best understanding of the key role played by the most important molecules, hormones, kinase cascade, cell communication up to the latest knowledge. An approach that we used is based on hybrid discrete-continuous models, where cells are considered as individual objects, intracellular regulatory networks are described with ordinary differential equations, extracellular concentrations with diffusion or diffusion-convection equations (see Figure 1). These modeling tools require the expertise of all team members to get the most qualitative satisfactory model. The obtained models will be applied particularly to describe normal and pathological hematopoiesis as well as immune response.
3.4 From hybrid dynamics to continuum mechanics
Hybrid discrete-continuous methods are well adapted to describe biological cells. However, they are not appropriate for the qualitative investigation of the corresponding phenomena. Therefore, hybrid model approach should be combined with continuous models. If we consider cell populations as a continuous medium, then cell concentrations can be described by reaction-diffusion systems of equations with convective terms. The diffusion terms correspond to a random cell motion and the reaction terms to cell proliferation, differentiation and death. We will continue our studies of stability, nonlinear dynamics and pattern formation. Theoretical investigations of reaction-diffusion models will be accompanied by numerical simulations and will be applied to study cell population dynamic.
3.5 Structured partial differential equations
Hyperbolic problems are also of importance when describing cell population dynamics. They are structured transport partial differential equations, in which the structure is a characteristic of the considered population, for instance age, size, maturity, etc. In the scope of multi-scale modeling, protein concentrations as structure variables can precisely indicate the nature of cellular events cells undergo (differentiation, apoptosis), by allowing a representation of cell populations in a multi-dimensional space. Several questions are still open in the study of this problem, yet we will continue our analysis of these equations by focusing in particular on the asymptotic behavior of the system (stability, oscillations) and numerical simulations.
3.6 Delay differential equations
The use of age structure in PDE often leads to a reduction (by integration over the age variable) to delay differential equations. Delay differential equations are particularly useful for situations where the processes are controlled through feedback loops acting after a certain time. For example, in the evolution of cell populations the transmission of control signals can be related to some processes as division, differentiation, maturation, apoptosis, etc. Delay differential equations offer good tools to study the behavior of the systems. Our main investigation will be the effect of perturbations of the parameters, as cell cycle duration, apoptosis, differentiation, self-renewal, etc., on the behavior of the system, in relation for instance with some pathological situations. The mathematical analysis of delay differential equations is often complicated and needs the development of new criteria to be performed.
3.7 Multi-scale modeling of the immune response
The main objective of this part is to develop models that make it possible to investigate the dynamics of the adaptive CD8 T cell immune response, and in particular to focus on the consequences of early molecular events on the cellular dynamics few days or weeks later: this would help developing predictive tools of the immune response in order to facilitate vaccine development and reduce costs. This work requires a close and intensive collaboration with immunologist partners.
We recently published a model of the CD8 T cell immune response characterizing differentiation stages, identified by biomarkers, able to predict the quantity of memory cells from early measurements, 39. In parallel, we improved our multiscale model of the CD8 T cell immune response, by implementing a full differentiation scheme, from naïve to memory cells, based on a limited set of genes and transcription factors.
Our first task will be to infer an appropriate gene regulatory network (GRN) using single cell data analysis (generate transcriptomics data of the CD8 T cell response to diverse pathogens), the previous biomarkers we identified and associated to differentiation stages, as well as piecewise-deterministic Markov processes (Ulysse Herbach's PhD thesis, ongoing).
Our second task will be to update our multiscale model by first implementing the new differentiation scheme we identified 39, and second by embedding CD8 T cells with the GRN obtained in our first task (see above). This will lead to a multi-scale model incorporating description of the CD8 T cell immune response both at the molecular and the cellular levels (Simon Girel's PhD thesis, ongoing).
In order to further develop our multiscale model, we will consider an agent-based approach for the description of the cellular dynamics. Yet, such models, coupled to continuous models describing GRN dynamics, are computationally expensive, so we will focus on alternative strategies, in particular on descriptions of the cellular dynamics through both continuous and discrete models, efficiently coupled. Using discrete models for low cell numbers and continuous (partial differential equations) models for large cell numbers, with appropriate coupling strategies, can lead to faster numerical simulations, and consequently can allow performing intense parameter estimation procedures that are necessary to validate models by confronting them to experimental data, both at the molecular and cellular scales.
The final objective will be to capture CD8 T cell responses in different immunization contexts (different pathogens, tumor) and to predict cellular outcomes from molecular events.
3.8 Dynamical network inference from single-cell data
Up to now, all of our multiscale models have incorporated a dynamical molecular network that was build “by hand” after a thorough review of the literature. It would be highly valuable to infer it directly from gene expression data. However, this remains very challenging from a methodological point of view. We started exploring an original solution for such inference by using the information contained within gene expression distributions. Such distributions can be acquired through novel techniques where gene expression levels are quantified at the single cell level. We propose to view the inference problem as a fitting procedure for a mechanistic gene network model that is inherently stochastic and takes not only protein, but also mRNA levels into account. This approach led to very encouraging results 40 and we will actively pursue in that direction, especially in the light of the foreseeable explosion of single cell data.
3.9 Leukemia modeling
Imatinib and other tyrosine kinase inhibitors (TKIs) have marked a revolution in the treatment of Chronic Myelogenous Leukemia (CML). Yet, most patients are not cured, and must take their treatment for life. Deeper mechanistic understanding could improve TKI combination therapies to better control the residual leukemic cell population. In a collaboration with the Hospital Lyon Sud and the University of Maryland, we have developed mathematical models that integrate CML and an autologous immune response (36, 37 and 38). These studies have lent theoretical support to the idea that the immune system plays a rôle in maintaining remission over long periods. Our mathematical model predicts that upon treatment discontinuation, the immune system can control the disease and prevent a relapse. There is however a possibility for relapse via a sneak-though mechanism 36. Research in the next four years will focus in the Phase III PETALS trial. In the PETALS trial, the second generation TKI Nilotinib is combined with Peg-IFN, an interferon that is thought to enhance the immune response. We plan to: 1) Adapt the model to take into account the early dynamics (first three months). 2) Use a mixed-effect approach to analyse the effect of the combination, and find population and individual parameters related to treatment efficacy and immune system response. 3) Optimise long-term treatment strategies to reduce or cease treatment and make personalised predictions based on mixed-effect parameters, to minimise the long-term probability of relapse.
4 Application domains
See the previous sections.
5 New results
Participants: [ All team members ].
5.1 Models of immune response
5.1.1 Modeling and characterization of inter-individual variability in CD8 T cell responses in mice
To develop vaccines, it is mandatory yet challenging to account for inter-individual variability during immune responses. Even in laboratory mice, T cell responses of single individuals exhibit a high heterogeneity that may come from genetic backgrounds, intra-specific processes (e.g., antigen-processing and presentation) and immunization protocols. To account for inter-individual variability in CD8 T cell responses in mice, we propose in 6 a dynamical model coupled to a statistical, nonlinear mixed effects model. Average and individual dynamics during a CD8 T cell response are characterized in different immunization contexts (vaccinia virus and tumor). On one hand, we identify biological processes that generate inter-individual variability (activation rate of naive cells, the mortality rate of effector cells, and dynamics of the immunogen). On the other hand, introducing categorical covariates to analyze two different immunization regimens, we highlight the steps of the response impacted by immunogens (priming, differentiation of naive cells, expansion of effector cells and generation of memory cells). The robustness of the model is assessed by confrontation to new experimental data. Our approach allows to investigate immune responses in various immunization contexts, when measurements are scarce or missing, and contributes to a better understanding of inter-individual variability in CD8 T cell immune responses.
5.1.2 Multiscale modeling of germinal center recapitulates the temporal transition from memory B cells to plasma cells differentiation as regulated by antigen affinity-based Tfh cell help
Germinal centers play a key role in the adaptive immune system since they are able to produce memory B cells and plasma cells that produce high affinity antibodies for an effective immune protection. The mechanisms underlying cell-fate decisions are not well understood but asymmetric division of antigen, B-cell receptor affinity, interactions between B-cells and T follicular helper cells (triggering CD40 signaling), and regulatory interactions of transcription factors have all been proposed to play a role. In addition, a temporal switch from memory B-cell to plasma cell differentiation during the germinal center reaction has been shown. To investigate if antigen affinity-based Tfh cell help recapitulates the temporal switch we implemented in 15 a multiscale model that integrates cellular interactions with a core gene regulatory network comprising BCL6, IRF4, and BLIMP1. Using this model, we show that affinity-based CD40 signaling in combination with asymmetric division of B-cells result in switch from memory B-cell to plasma cell generation during the course of the germinal center reaction. We also show that cell fate division is unlikely to be (solely) based on asymmetric division of Ag but that BLIMP1 is a more important factor. Altogether, our model enables to test the influence of molecular modulations of the CD40 signaling pathway on the production of germinal center output cells.
5.1.3 Modeling the relationship between antibody-dependent enhancement and disease severity in secondary dengue infection
Sequential infections with different dengue serotypes (DENV-1, 4) significantly increase the risk of a severe disease outcome (fever, shock and hemorrhagic disorders). Two hypotheses have been proposed to explain the severity of dengue disease: (1) antibody-dependent enhancement (ADE); (2) original T cell antigenic sin. In 9, we explored the first hypothesis through mathematical modeling. The proposed model reproduces the dynamic of susceptible and infected target cells, and dengue virus in scenarios of infection-neutralizing and-enhancing antibodies competition induced by two distinct serotypes of dengue virus. The enhancement and neutralization functions are derived from basic concepts of chemical reactions and used to mimic binding to the virus by two distinct populations of antibodies. The analytic study of the model showed the existence of two equilibriums, a disease-free equilibrium and an endemic one. We performed the asymptotic stability analysis for these two equilibriums. The local asymptotic stability of the endemic-equilibrium corresponds to the occurrence of dengue hemorrhagic fever (DHF) or dengue shock syndrome (DSS). We defined the time t DHF at which DHF/DSS occurs as the time when the infected cells (or the virus) population reaches a maximum. This corresponds to the time at which maximum enhancing activity for dengue infection appears. The critical time t DHF was calculated from the model to be few days after the occurrence of the infection, which corresponds to what is observed in the literature. Finally, using as output the basic reproduction number we were able to rank the contribution of each parameter of the model. In particular, we have highlighted the evidence of the role of enhancing antibodies in cross-reaction and the occurrence of DHF/DSS.
5.2 Single-cell and cell differentiation
5.2.1 Practical identifiability in the frame of nonlinear mixed effects models: the example of the in vitro erythropoiesis
Background Nonlinear mixed effects models provide a way to mathematically describe experimental data involving a lot of inter-individual heterogeneity. In order to assess their practical identifiability and estimate confidence intervals for their parameters, most mixed effects modelling programs use the Fisher Information Matrix. However, in complex nonlinear models, this approach can mask practical unidentifiabilities. We rather propose in 10 a multistart approach, and use it to simplify our model by reducing the number of its parameters, in order to make it identifiable. Our model describes several cell populations involved in vitro differentiation of chicken erythroid progenitors grown in the same environment. Inter-individual variability observed in cell population counts is explained by variations of the differentiation and proliferation rates between replicates of the experiment. Alternatively, we test a model with varying initial condition. We conclude by relating experimental variability to precise and identifiable variations between the replicates of the experiment of some model parameters.
5.2.2 Entropy as a measure of variability and stemness in single-cell transcriptomics
We propose in 11 a simple typology that should help non-specialists readers to better grasp the relevance of the term "entropy" for the analysis of single cell transcriptomics data, and differentiate its various occurrences.
5.2.3 Reduction of a stochastic model of gene expression: Lagrangian dynamics gives access to basins of attraction as cell types and metastabilty
Differentiation is the process whereby a cell acquires a specific phenotype, by differential gene expression as a function of time. This is thought to result from the dynamical functioning of an underlying Gene Regulatory Network (GRN). The precise path from the stochastic GRN behavior to the resulting cell state is still an open question. In 18 we propose to reduce a stochastic model of gene expression, where a cell is represented by a vector in a continuous space of gene expression, to a discrete coarse-grained model on a limited number of cell types. We develop analytical results and numerical tools to perform this reduction for a specific model characterizing the evolution of a cell by a system of piecewise deterministic Markov processes (PDMP). Solving a spectral problem, we find the explicit variational form of the rate function associated to a Large deviations principle, for any number of genes. The resulting Lagrangian dynamics allows us to define a deterministic limit of which the basins of attraction can be identified to cellular types. In this context the quasipotential, describing the transitions between these basins in the weak noise limit, can be defined as the unique solution of an Hamilton-Jacobi equation under a particular constraint. We develop a numerical method for approximating the coarse-grained model parameters, and show its accuracy for a symmetric toggle-switch network. We deduce from the reduced model an approximation of the stationary distribution of the PDMP system, which appears as a Beta mixture. Altogether those results establish a rigorous frame for connecting GRN behavior to the resulting cellular behavior, including the calculation of the probability of jumps between cell types (see also 26).
5.2.4 Reverse engineering of a mechanistic model of gene expression using metastability and temporal dynamics
Differentiation can be modeled at the single cell level as a stochastic process resulting from the dynamical functioning of an underlying Gene Regulatory Network (GRN), driving stem or progenitor cells to one or many differentiated cell types. Metastability seems inherent to differentiation process as a consequence of the limited number of cell types. Moreover, mRNA is known to be generally produced by bursts, which can give rise to highly variable non-Gaussian behavior, making the estimation of a GRN from transcriptional profiles challenging. In the article 19, we present CARDAMOM (Cell type Analysis from scRna-seq Data achieved from a Mixture MOdel), a new algorithm for inferring a GRN from timestamped scRNA-seq data, which crucially exploits these notions of metastability and transcriptional bursting. We show that such inference can be seen as the successive resolution of as many regression problem as timepoints, after a preliminary clustering of the whole set of cells with regards to their associated bursts frequency. We demonstrate the ability of CARDAMOM to infer a reliable GRN from in silico expression datasets, with good computational speed. To the best of our knowledge, this is the first description of a method which uses the concept of metastability for performing GRN inference.
5.3 Periodic hematological disorders
5.3.1 Why are periodic erythrocytic diseases so rare in humans?
Many studies have shown that periodic erythrocytic (red blood cell linked) diseases are extremely rare in humans. To explain this observation, we develop in 2 a simple model of erythropoiesis in mammals and investigate its stability in the parameter space. A bifurcation analysis enables us to sketch stability diagrams in the plane of key parameters. Contrary to some other mammal species such as rabbits, mice or dogs, we show that human-specific parameter values prevent periodic oscillations of red blood cells levels. In other words, human erythropoiesis seems to lie in a region of parameter space where oscillations exclusively concerning red blood cells cannot appear. Further mathematical analysis show that periodic oscillations of red blood cells levels are highly unusual and if exist, might only be due to an abnormally high erythrocytes destruction rate or to an abnormal hematopoietic stem cell commitment into the erythrocytic lineage. We also propose numerical results only for an improved version of our approach in order to give a more realistic but more complex approach of our problem.
5.3.2 Periodic solutions for a nonautonomous mathematical model of hematopoietic stem cell dynamics
The main purpose of the paper 1 is to study the existence of periodic solutions for a nonautonomous differential-difference system describing the dynamics of hematopoietic stem cell (HSC) population under some external periodic regulatory factors at the cellular cycle level. The starting model is a nonautonomous system of two age-structured partial differential equations describing the HSC population in quiescent (G0) and proliferating (G1, S, G2 and M) phase. We are interested in the effects of periodically time varying coefficients due for example to circadian rhythms or to the periodic use of certain drugs, on the dynamics of HSC population. The method of characteristics reduces the age-structured model to a nonautonomous differential-difference system. We prove under appropriate conditions on the parameters of the system, using topological degree techniques and fixed-point methods, the existence of periodic solutions of our model.
5.4 Protein aggregation and neurodegenerative diseases
5.4.1 A reaction-diffusion model of spatial propagation of A beta oligomers in early stage Alzheimer’s disease
The misconformation and aggregation of the protein Amyloid-Beta (A) is a key event in the propagation of Alzheimer's Disease (AD). Different types of assemblies are identified, with long fibrils and plaques deposing during the late stages of AD. In the earlier stages, the disease spread is driven by the formation and the spatial propagation of small amorphous assemblies called oligomers. We propose in 4 a model dedicated to studying those early stages, in the vicinity of a few neurons and after a polymer seed has been formed. We build a reaction-diffusion model, with a Becker-Döring-like system that includes fragmentation and size-dependent diffusion. We hereby establish the theoretical framework necessary for the proper use of this model, by proving the existence of solutions using a fixed-point method.
5.4.2 Mathematical modeling of protein self-aggregation and conversion
Following the discovery that prions are self-replicating assemblies of proteins, mathematical models were developed in parallel with experimental methods in order to conceptualize this phenomenon. After four decades of research, much insight has been gained into protein misfolding processes and the neurodegenerative diseases which they cause. However, the complexity of these systems remains undiminished and the classical models of protein aggregation are now showing their limits. In particular, the observed spectrum of objects generated during the propagation of prions is not accounted for in any model, whereas it keeps expanding under the development of experimental tools. In the manuscript 27, our aim is to identify the weaknesses of classical models of prion propagation in light of recent biological evidence. We then suggest modified and improved models, by including different processes, by adding more levels of organization and more diversity to protein aggregates. Three main topics are presented, corresponding to different instances of protein aggregation and different biological systems. The first part takes place in the mammalian nervous system, and investigates the self-aggregation kinetics of PrP, the aptly named prion protein. In the second part, we model the replication of protein aggregates inside dividing yeast cells, by proposing a novel multi-scale approach. In the third part, we explore the spatial propagation of small protein oligomers in the early stages of Alzheimer’s Disease. These three axes are linked by the central role of structural diversity in the global protein aggregation system.
5.5 Improving cancer treatments via dynamical biophysical models
Despite significant advances in oncological research, cancer nowadays remains one of the main causes of mortality and morbidity worldwide. New treatment techniques, as a rule, have limited efficacy, target only a narrow range of oncological diseases, and have limited availability to the general public due their high cost. An important goal in oncology is thus the modification of the types of antitumor therapy and their combinations, that are already introduced into clinical practice, with the goal of increasing the overall treatment efficacy. One option to achieve this goal is optimization of the schedules of drugs administration or performing other medical actions. Several factors complicate such tasks: the adverse effects of treatments on healthy cell populations, which must be kept tolerable; the emergence of drug resistance due to the intrinsic plasticity of heterogeneous cancer cell populations; the interplay between different types of therapies administered simultaneously. Mathematical modeling, in which a tumor and its microenvironment are considered as a single complex system, can address this complexity and can indicate potentially effective protocols, that would require experimental verification. In the review 13, we consider classical methods, current trends and future prospects in the field of mathematical modeling of tumor growth and treatment. In particular, methods of treatment optimization are discussed with several examples of specific problems related to different types of treatment.
5.6 Blood clotting decreases pulmonary circulation during the coronavirus disease
Spontaneous blood clotting in pulmonary circulation caused by thrombo-inflammation is one of the main mortality causes during the COVID-19 disease. Blood clotting leads to reduced pulmonary circulation and blood oxygenation. Lung inflammation can be evaluated with noninvasive diagnostic techniques. However, the correlation of the severity of the inflammation with the pulmonary blood flow has not been established. To address this question, in 16, we develop a multiscale model taking into account the interaction of a local model of thrombus growth with 1D hemodynamics in a vessel network. Flux reduction depending on the level of lung obstruction is evaluated. In particular, the model obtains that an obstruction level of 5% leads to a 12% reduction of blood flux. The suggested approach can be used to investigate the interaction of blood clotting and flow not only in the pulmonary network but also in other complex vessel networks.
5.7 Patient-specific modelling of blood coagulation
Blood coagulation represents one of the most studied processes in biomedical modelling. However, clinical applications of this modelling remain limited because of the complexity of this process and because of large inter-patient variation of the concentrations of blood factors, kinetic constants and physiological conditions. Determination of some of these patients-specific parameters is experimentally possible, but it would be related to excessive time and material costs impossible in clinical practice. We propose in 17 a methodological approach to patient-specific modelling of blood coagulation. It begins with conventional thrombin generation tests allowing the determination of parameters of a reduced kinetic model. Next, this model is used to study spatial distributions of blood factors and blood coagulation in flow, and to evaluate the results of medical treatment of blood coagulation disorders.
5.8 Models in epidemiology
5.8.1 Vaccination in a two-group epidemic model
Epidemic progression depends on the structure of the population. We study in 5 a two-group epidemic model with the difference between the groups determined by the rate of disease transmission. The basic reproduction number, the maximal and the total number of infected individuals are characterized by the proportion between the groups. We consider different vaccination strategies and determine the outcome of the vaccination campaign depending on the distribution of vaccinated individuals between the groups.
5.8.2 Epidemic progression and vaccination in a heterogeneous population. Application to the Covid-19 epidemic
The paper 20 is devoted to a compartmental epidemiological model of infection progression in a heterogeneous population which consists of two groups with high disease transmission (HT) and low disease transmission (LT) potentials. Final size and duration of epidemic, the total and current maximal number of infected individuals are estimated depending on the structure of the population. It is shown that with the same basic reproduction number in the beginning of epidemic, its further progression depends on the ratio between the two groups. Therefore, fitting the data in the beginning of epidemic and the determination of are not sufficient to predict its long time behaviour. Available data on the Covid-19 epidemic allows the estimation of the proportion of the HT and LT groups. Estimated structure of the population is used for the investigation of the influence of vaccination on further epidemic development. The result of vaccination strongly depends on the proportion of vaccinated individuals between the two groups. Vaccination of the HT group acts to stop the epidemic and essentially decreases the total number of infected individuals at the end of epidemic and the current maximal number of infected individuals while vaccination of the LT group only acts to protect vaccinated individuals from further infection.
5.8.3 Traveling waves of a differential-difference diffusive Kermack-McKendrick epidemic model with age-structured protection phase
We consider in 3 a general class of diffusive Kermack-McKendrick SIR epidemic models with an age-structured protection phase with limited duration, for example due to vaccination or drugs with temporary immunity. A saturated incidence rate is also considered which is more realistic than the bilinear rate. The characteristics method reduces the model to a coupled system of a reaction-diffusion equation and a continuous difference equation with a time-delay and a nonlocal spatial term caused by individuals moving during their protection phase. We study the existence and non-existence of non-trivial traveling wave solutions. We get almost complete information on the threshold and the minimal wave speed that describes the transition between the existence and non-existence of non-trivial traveling waves that indicate whether the epidemic can spread or not. We discuss how model parameters, such as protection rates, affect the minimal wave speed. The difficulty of our model is to combine a reaction-diffusion system with a continuous difference equation. We deal with our problem mainly by using Schauder's fixed point theorem. More precisely, we reduce the problem of the existence of non-trivial traveling wave solutions to the existence of an admissible pair of upper and lower solutions.
5.9 Nonlocal reaction-diffusion models and population dynamics
5.9.1 Nonlocal reaction-diffusion models of heterogeneous wealth distribution
Dynamics of human populations can be affected by various socio-economic factors through their influence on the natality and mortality rates, and on the migration intensity and directions. In 7 we study an economic–demographic model which takes into account the dependence of the wealth production rate on the available resources. In the case of nonlocal consumption of resources, the homogeneous-in-space wealth–population distribution is replaced by a periodic-in-space distribution for which the total wealth increases. For the global consumption of resources, if the wealth redistribution is small enough, then the homogeneous distribution is replaced by a heterogeneous one with a single wealth accumulation center. Thus, economic and demographic characteristics of nonlocal and global economies can be quite different in comparison with the local economy.
5.9.2 Existence and dynamics of strains in a nonlocal reaction-diffusion model of viral evolution
In 8, we develop a mathematical framework for predicting and quantifying virus diversity evolution during infection of a host organism. It is specified as a virus density distribution with respect to genotype and time governed by a reaction-diffusion integro-differential equation taking virus mutations, replication, and elimination by immune cells and medical treatment into account. Conditions for the existence of virus strains that correspond to localized density distributions in the space of genotypes are determined. It is shown that common viral evolutionary traits like diversification and extinction are driven by nonlocal interactions via immune responses, target-cell competition, and therapy. This provides us with a mechanistic explanation for clinically relevant properties like immune escape and drug resistance selection, and allows us to link virus genotypes to phenotypes.
5.9.3 Pattern formation in a three-species cyclic competition model
In nature, different species compete among themselves for common resources and favorable habitat. Therefore, it becomes really important to determine the key factors in maintaining the biodiversity. Also, some competing species follow cyclic competition in real world where the competitive dominance is characterized by a cyclic ordering. In 14, we study the formation of a wide variety of spatiotemporal patterns including stationary, periodic, quasi-periodic and chaotic population distributions for a diffusive Lotka-Volterra type three-species cyclic competition model with two different types of cyclic ordering. For both types of cyclic ordering, the temporal dynamics of the corresponding non-spatial system show the extinction of two species through global bifurcations such as homoclinic and heteroclinic bifurcations. For the spatial system, we show that the existence of Turing patterns is possible for a particular cyclic ordering, while it is not the case for the other cyclic ordering through both the analytical and numerical methods. Further, we illustrate an interesting scenario of short-range invasion as opposed to the usual invasion phenomenon over the entire habitat. Also, our study reveals that both the stationary and dynamic population distributions can coexist in different parts of a habitat. Finally, we extend the spatial system by incorporating nonlocal intra-specific competition terms for all the three competing species. Our study shows that the introduction of nonlocality in intra-specific competitions stabilizes the system dynamics by transforming a dynamic population distribution to stationary. Surprisingly, this nonlocality-induced stationary pattern formation leads to the extinction of one species and hence, gives rise to the loss of biodiversity for intermediate ranges of nonlocality. However, the biodiversity can be restored for sufficiently large extent of nonlocality.
5.9.4 Method of monotone solutions for reaction-diffusion equations
Existence of solutions of reaction-diffusion systems of equations in unbounded domains is studied by the Leray-Schauder (LS) method based on the topological degree for elliptic operators in unbounded domains and on a priori estimates of solutions in weighted spaces, 21. We identify some reaction-diffusion systems for which there exist two subclasses of solutions separated in the function space, monotone and nonmonotone solutions. A priori estimates and existence of solutions are obtained for monotone solutions allowing to prove their existence by the LS method. Various applications of this method are given.
5.9.5 Solvability of some integro-differential equations with anomalous diffusion and transport
The article 22 deals with the existence of solutions of an integro-differential equation in the case of anomalous diffusion with the negative Laplace operator in a fractional power in the presence of the transport term. The proof of existence of solutions is based on a fixed-point technique. Solvability conditions for elliptic operators without the Fredholm property in unbounded domains are used. We discuss how the introduction of the transport term impacts the regularity of solutions.
5.9.6 Analysis and numerical simulations of a reaction-diffusion model with fixed active bodies
We propose in 23 an interaction model for two substances (molecules) of concentrations and . The substance is assumed to be involved in the growth process of , and in contrast, the substance inhibits the production of . Our model is based on a reaction-diffusion system for the interaction of two considered substances (molecules). We analyze its well-posedness and perform a numerical scheme to simulate the behavior of the solutions. As an application, we investigate the role of A-oligomers in the early stage of Alzheimer's disease propagation, more precisely for the impact of A-oligomers in neuron impairment as studied in [M. Andrade-Restrepo et al., Modeling the spatial propagation of A oligomers in Alzheimer's disease, in CEMRACS 2018 - Numerical and Mathematical Modeling for Biological and Medical Applications: Deterministic, Probabilistic and Statistical Descriptions, Marseille, France, 2018, pp. 1-10].
5.9.7 Turing instability in an economic–demographic dynamical system may lead to pattern formation on a geographical scale
Spatial distribution of the human population is distinctly heterogeneous, e.g. showing significant difference in the population density between urban and rural areas. In the historical perspective, i.e. on the timescale of centuries, the emergence of densely populated areas at their present locations is widely believed to be linked to more favourable environmental and climatic conditions. In 24, we challenge this point of view. We first identify a few areas at different parts of the world where the environmental conditions (quantified by the temperature, precipitation and elevation) show a relatively small variation in space on the scale of thousands of kilometres. We then examine the population distribution across those areas to show that, in spite of the approximate homogeneity of the environment, it exhibits a significant variation revealing a nearly periodic spatial pattern. Based on this apparent disagreement, we hypothesize that there may exist an inherent mechanism that may lead to pattern formation even in a uniform environment. We consider a mathematical model of the coupled demographic-economic dynamics and show that its spatially uniform, locally stable steady state can give rise to a periodic spatial pattern due to the Turing instability, the spatial scale of the emerging pattern being consistent with observations. Using numerical simulations, we show that, interestingly, the emergence of the Turing patterns may eventually lead to the system collapse.
5.9.8 Global attractor in alpha-norm for some partial functional differential equations of neutral and retarded type
The aim of the work 25 is to study the existence of a global attractor for some partial neutral functional differential equations; the convergence of all the solutions to the attractor is given in terms of the alpha-norm which is more important than the classical norm. Firstly, we show some interesting properties on the semigroup solution like the asymptotic smoothness. Secondly, when the semigroup is compact dissipative, then we show the existence of the global attractor. For illustration, an application is provided for some model arising in physical systems.
5.9.9 Longtime behavior of a second order finite element scheme simulating the kinematic effects in liquid crystal dynamics
We consider in 12 an unconditional fully discrete finite element scheme for a nematic liquid crystal flow with different kinematic transport properties. We prove that the scheme converges towards a unique critical point of the elastic energy subject to the finite element subspace, when the number of time steps go to infinity while the time step and mesh size are fixed. A Lojasiewicz type inequality, which is the key for getting the time asymptotic convergence of the whole sequence furnished by the numerical scheme, is also derived.
6 Partnerships and cooperations
6.1 International initiatives
6.1.1 Associate Teams in the framework of an Inria International Lab or in the framework of an Inria International Program
Inria-Brazil project: MoCoVec
Participants: Pierre-Alexandre Bliman, Mostafa Adimy, Cláudia Pio Ferreira.
-
Title:
Modelling and Biological Control of Vector-Borne Diseases: the case of Malaria and Dengue
-
Partner Institution(s) and Coordinators:
- INRIA-MAMBA team, CRI Paris
- INRIA-Dracula team, CRI Lyon
- FAPESP Sao Paolo, Brazil
-
Date/Duration:
January 2022 / 3 years
-
Additionnal info/keywords:
Taking into account all the infectious disease spread worldwide, vector-borne diseases account for over 17%. For a huge part of them, no efficient vaccine is available, and control efforts must be done on the vector population. Focusing on dengue and malaria, two diseases transmitted by vector mosquito and which cause high morbidity and mortality around the world, this project aims to model disease transmission, its spread and control, in a context of climatic and environmental change. For this, the main drives of disease transmission will be addressed to understand which factors modulate the spatio-temporal patterns observed, especially in Brazil. Combining techniques of data analysis with mathematical models and control theory, the plan is to work on data analysis to define potential biotic and abiotic factors that drives malaria and dengue disease dynamics; to study and model the effects of seasonality on the spread of the diseases; to understand spatial aspects of the transmission through the setup of models capable to account for nonlocal and heterogeneous aspect; and to analyse alternative approaches of mosquito control, especially the biological control methods based on sterile mosquitoes or on infection by bacterium that reduces the vectorial capacity / Control theory; differential equations; temporal series analysis; biological control.
6.1.2 STIC/MATH/CLIMAT AmSud project
AmSud project: NEMBICA
Participants: Pierre-Alexandre Bliman, Mostafa Adimy, Yves Dumont, Alain Rapaport, Nicolas Vauchelet, Hernán G. Solari, Juan Pablo Aparicio, Ziomara Gerdtzen, Irene Duarte Gandica, Daiver Cardona Salgado, Olga Vasilieva, Christian Schaerer.
-
Title:
NEw Methods for BIological Control of the Arboviruses
-
Partner Institution(s) and Coordinators:
- INRIA-MAMBA team CRI Paris
- INRIA-Dracula team, CRI Lyon
- CIRAD
- UMR MISTEA
- CNRS
- Universidad de Buenos Aires and Universidad Nacional de Salta, Argentina
- Universidad de Chile, Chile
- Universidad del Quindio, Universidad Autónoma de Occidente and Universidad del Valle, Colombia
- National University of Asuncion, Paraguay
-
Date/Duration:
January 2019 / 2 years
-
Additionnal info/keywords:
This project addresses open problems about non autonomous systems of Delay Differential Equations modeling some phenomena from life sciences, namely, a metapopulations version of the Nicholson equations and models of competition in a stirred chemostat. Nevertheless, the ideas and methods could be certainly extended in several ways, and we also expect to make progress in topics as the (non autonomous) topological linearization problem and the possibility of converse results for persistence.
AmSud project: TOMENADE
Participants: Mostafa Adimy, Frédéric Mazenc, Daniel Sepúlveda, Pierluigi Benevieri.
-
Title:
Topological Methods and Non Autonomous Dynamics for Delay Differential Equations
-
Partner Institution(s) and Coordinators:
- INRIA-Dracula team, CRI Lyon
- Laboratoire des Signaux et Systèmes (L2S) – CNRS – CentraleSupelec
- Universidad Tecnológica Metropolitana, Chile
- Universidade de Sao Paulo, Brazil
-
Date/Duration:
January 2021 / 2 years
-
Additionnal info/keywords:
The present project is concerned with new strategies of biological control of the spread of many and important diseases transmitted by mosquitoes of the genus Aedes, which put at risk considerable portions of the human population and infect millions of people every year. The aim is to elaborate and analyze pertinent models, and to evaluate qualitatively and quantitatively different control strategies, with the goal of understanding the key aspects and parameters of the dynamics, testing concepts, estimating feasibility, identifying risks and reducing cost.
6.1.3 Participation in other International Programs
ECOS-Sud France-Chilie, C20E03
Participants: Erwan Hingant, Mauricio Sepúlveda, Luis M. Villada, Romain Yvinec, Leon Matar Tine, Laurent Pujo-Menjouet.
-
Title:
Coarsening dynamics: numerical and theoretical analysis of the Lifchitz-Slyozov equation with nucleation and applications to biology.
-
Partner Institution(s):
- Inria ANACONDA, FRANCE
- Institut Denis Poisson–Université d’Orléans, FRANCE
- Universidad del Bio-Bio, Concepcion, CHILIE
-
Date/Duration:
January 2021 / 3 years
-
Additionnal info/keywords:
Principal investigator : Romain Yvinec, MUSCA.
6.2 International research visitors
6.2.1 Visits of international scientists
Other international visits to the team
Abdennasser Chekroun
-
Status
Associate professor
-
Institution of origin:
University Abou Bekr Belkaid of Tlemcen
-
Country:
Algeria
-
Dates:
December 2021-January 2022
-
Context of the visit:
First winner of the Maurice Audin chair chair
-
Mobility program/type of mobility:
Research stay: During his visit, A. Chekroun worked with L. Pujo-Menjouet on bone formation dynamical models
6.3 European initiatives
6.3.1 FP7 & H2020 projects
COSMIC (606)
-
Title:
COmbatting disorders of adaptive immunity with Systems MedICine
-
Duration:
2018-2021
-
Coordinator:
Antpoine van Kampen
-
Partners:
- Bioinformatics Laboratory, Dept. of Pathology and Rheumatology and clinical immunology, ACADEMISCH MEDISCH CENTRUM BIJ DE UNIVERSITEIT VAN AMSTERDAM (Netherlands)
- ANAXOMICS BIOTECH S.L. (ANX) (Spain)
- Biotecture (Netherlands)
- ELEVATE BV (Netherlands)
- ETHNIKO KENTRO EREVNAS KAI TECHNOLOGIKIS ANAPTYXIS (Greece)
- HELMHOLTZ-ZENTRUM FUR
- INFEKTIONSFORSCHUNG GMBH (Germany)
- IBM RESEARCH GMBH (Switzerland)
- KAROLINSKA INSTITUTET (Sweden)
- REDOXIS AB (Sweden)
-
Inria contact:
Olivier Gandrillon
-
Summary:
COSMIC delivers the next generation of systems medicine professionals who successfully combat complex human disorders. We will focus on B-cell lymphoma and rheumatoid arthritis, diseases that originate from abnormal functioning of the adaptive immune system, in particular the germinal center. COSMIC develops and integrates experimental and computational approaches, and establishes a unique cross-fertilization between oncology and auto-immunity.
6.4 National initiatives
6.4.1 ANR
ANR Prio Diff
-
Title:
Impact of replication and structural diversification of prions on their cerebral dissemination
-
Partner Institution(s):
- Inrae Jouy-en-Josas, France
- Inrae Toulouse, France
- CEA, Fontenay aux Roses, France
- Institut Camille Jordan, France
-
Date/Duration:
July 2021-June 2025
-
Additionnal info/keywords:
Prions are lethal proteinaceous pathogens with major public-health risks due to their zoonotic and iatrogenic potential. They are composed of aggregated, misfolded conformers of the host-encoded prion protein that progressively deposit in the brain by a self-perpetuating reaction. The underlying molecular mechanisms of replication and tissue dissemination remain mostly elusive. Our objective is to model these processes entirely based on recent advances that prion aggregates are conformationally heterogeneous and dynamic rather than uniform and static. To achieve this, we will map in prion-infected brain the structural diversification-to-bioactivity/neurotoxicity landscape of prion assemblies in a spatiotemporal manner and mathematically build a multiscale model of diversification and lesion spreading. The goal is to generate an open access model capable of predicting the disease progression and identify key elementary process for therapeutics intervention and early diagnostics. / Keywords: interactions hôtes pathogènes, infectiologie, modélisation prion, tissue diffusion, neurotropism.
Digitbio
-
Title:
MP DIGIT-BIO, AMI 2021
-
Partner Institution(s):
- Inrae Jouy-en-Josas, France
- Inria, Dracula team, France
-
Date/Duration:
September 2021-August 2023
-
Additionnal info/keywords:
Ce projet a pour but de permettre d’explorer pour la première fois dans le champ des maladies neurodégénératives comment la dynamique des assemblages de PrPSc régit la dissémination, la ségrégation et l’accumulation de certaines sous-populations d’assemblages de PrPSc et conduit à l’apparition d’une structure souche-spécifique ainsi que de possibles fronts de propagation / Interactions hôtes pathogènes, infectiologie, modélisation prion, tissue diffusion, neurotropism.
ANR SinCity
-
Title:
Single cell transcriptomics on genealogically identified differentiating cells
-
Partner Institution(s):
- Laboratoire de biologie moléculaire de la cellule / ENS de Lyon
- Department of Chemistry and Applied Biosciences Institute for Chemical and Bioengineerin Institute for Chemical and Bioengineering/ETH
-
Date/Duration:
2017-2021
- Olivier Gandrillon participates in the ANR MEMOIRE (head Jacqueline Marvel) dedicated to “MultiscalE MOdeling of CD8 T cell Immune REsponses”, 2018-2021.
- Thomas is the Partner for ANR PLUME led by Marie Manceau (CNRS and Collège de France) dedicated to “Molecular and morphogenetic control of feather pattern formation”.
6.4.2 Other projects
- Thomas Lepoutre is a member of the ERC MESOPROBIO (head Vincent Calvez) dedicated to "Mesoscopic models for propagation in biology", 2015-2021.
6.5 Regional initiatives
INGERENCE
-
Title:
INferring GEne REgulatory NEtworks from single CEll Data to improve vaccine design
-
Date/Duration:
2018-2021.
-
Participants:
Olivier Gandrillon and Fabien Crauste
Mecan'os
-
Title:
Si tu ne peux pas l'avoir, (re)construis le !
-
Partner Institution(s):
- Institut Camille Jordan, France
- CUNY, New-York, USA
- university Abou Bekr Belkaid of Tlemcen, Algeria
-
Date/Duration:
September 2021-August 2023
-
Additionnal info/keywords:
La croissance rapide de la population gériatrique, qui est souvent atteinte de perte dégénérative de l’os, associée à une forte augmentation du nombre de personnes subissant une chirurgie de reconstruction osseuse (accident de voiture ou cancer des os), va permettre au marché des prothèses osseuses d’atteindre la somme de 4 milliards de dollars en 2025. À l’heure actuelle, ce marché est dominé par des matériaux synthétiques qui, malheureusement, présentent un fort risque de mauvaise intégration squelettique. Le remplacement de ces prothèses induit de nouvelles interventions chirurgicales et donc une augmentation des dépenses de santé. Nous pensons donc qu’il est grand temps de s’intéresser aux prochaines générations d’implants. Pour cette raison, notre équipe de bio-ingénieurs (USA) et mathématiciens (France et Algérie) est en train de développer un procédé de construction des prothèses de nouvelle génération adaptables à chaque personne. Partant du principe que la nature ne peut pas être égalée dans son inventivité, nous sommes convaincus que la solution viendra de la création d’implants biocompatibles par un contrôle numérique de l’expression des gènes des cellules osseuses venant des patients eux-mêmes. Étant donné que notre collaboration s’est déjà avérée fructueuse avec des donneurs de cellules âgés de 20 ans, nous souhaitons travailler en élargissant drastiquement la tranche d’âge. À cette fin, notre volonté est de renforcer notre collaboration et nos interactions pour apporter une solution rapide, efficace et adaptée aux personnes qui nécessite une chirurgie de reconstruction osseuse.
micrOS-macrOS
-
Title:
modélisation multi-échelle de l'os
-
Partner Institution(s):
- Institut Camille Jordan, France
- CUNY, New-York, USA
- university Abou Bekr Belkaid of Tlemcen, Algeria
-
Date/Duration:
September 2021-August 2023
-
Additionnal info/keywords:
Notre projet a pour objectif d’apporter un nouvel éclairage sur le rôle des micro-ARN dans la construction d’implants osseux de nouvelle génération. L’originalité de notre approche est de prédire quantitativement les résultats expérimentations afin de (1) réduire le nombre d’essais précliniques et (2) établir un cadre unique de personnalisation de régénération de tissu osseux humain.
- Thomas Lepoutre and Olivier Gandrillon have been granted and IXXI project on relaxation experiments for gene expression.
7 Dissemination
7.1 Promoting scientific activities
7.1.1 Scientific events: organisation
Member of the organizing committees
- Vitaly Volpert: Organization of the online workshop “Mathematical modelling in biomedicine”, October 25-29, 2021
- Laurent Pujo-Menjouet: Conference, SMB, July 2021, California, USA
- Laurent Pujo-Menjouet: Workshop Bonitos, Institut Camille Jordan, Lyon France
7.1.2 Journal
Member of the editorial boards
- Vitaly Volpert: Editor in chief of the journal “Mathematical modelling of natural Phenomena”.
- Laurent Pujo-Menjouet: Journal of theoretical biology
- Laurent Pujo-Menjouet: Plos One
- Laurent Pujo-Menjouet: Mathematical Modelling of Natural Phenomena journal
- Laurent Pujo-Menjouet: MDPI
- Mostafa Adimy: Mathematical Modelling of Natural Phenomena journal
- Mostafa Adimy: Modelling - MDPI
- Mostafa Adimy: JNSA
7.1.3 Invited talks
- Mostafa Adimy: International online workshop on Mathematical Modelling in Biomedicine, Moscow, Russia, 25-29 octobre 2021
- Mostafa Adimy: 1st International E-Conference on Differential Equations and Applications (IE-CDEA 2021), Fez, Maroc, 24-25 septembre 2021
- Mostafa Adimy: VI Latin American Congress of Mathematicians (CLAM2021), Montevideo, Uruguay, 13-17 septembre 2021
- Samuel Bernard: EWM-EMS Summer School on Multi-scale Modeling for Pattern Formation in Biological Systems (Web), 19 July - 23 July 2021
7.2 Teaching - Supervision - Juries
7.2.1 Supervision
- PhD in progress: Kyriaki Dariva , “Modélisation mathématique des interactions avec le système immunitaire en leucémie myéloide chronique”. Université Lyon 1, since September 2018, supervisor: Thomas Lepoutre
- PhD in progress: Alexey Koshkin, “Inferring gene regulatory networks from single cell data”, ENS de Lyon, until December 2021, supervisors: Olivier Gandrillon and Fabien Crauste
- PhD in progress: Paul Lemarre, “Modélisation des souches de prions”. Université Lyon 1, until May 2021, supervisors: Laurent Pujo-Menjouet et Suzanne Sindi (University of California, Merced)
- PhD in progress: Léonard Dekens, “Adaptation d'une population avec une reproduction sexuée à un environnement hétérogène : modélisation mathématique et analyse asymptotique dans un régime de petite variance”, Université Lyon 1, since September 2019, supervisor: Vincent Calvez.
- PhD in progress: Mete Demircigil, “Etude du mouvement collectif chez Dictyostelium Discoideum et autres espèces. Modélisation, Analyse et Simulation”, ENS-Lyon, since September 2019, supervisor: Vincent Calvez.
- PhD in progress: Ghada Abi Younes, “Modélisation mathématique des maladies inflammatoires”, Université Lyon, since November 2019, supervisor: Vitaly Volpert.
- PhD in progress: Elias Ventre, “Paysage et trajectoire - des réseaux de régulation génique aux trajectoires cellulaires", ENS, since October 2019, supervisors: Olivier Gandrillons, Thibault Espinasse and Thomas Lepoutre.
- PhD in progress: Cheikh Gueye, “Problèmes inverses pour l'estimation de paramètre de modèles mathématiques”, Université Lyon, since October 2019, supervisors: Laurent Pujo-Menjouet and Léon Tine.
- PhD in progress: Matteo Bouvier (CIFRE with the Vidium company), supervisor: Olivier Gandrillon.
- PhD in progress: Margaux Prieux, supervisors: Olivier Gandrillon and Jacqueline Marvel.
- PhD supervision: Aquilina Al Khouri, since April 2020, contract interrupted in October 2021, supervisors: Samuel Bernard and Jonathan Rouzaud-Cornabas.
- Post-doc: Madge Martin, supervisors: Olivier Gandrillon and Fabien Crauste.
7.2.2 Juries
- Alexey Koshkin, “Inferring gene regulatory networks from single cell data” (Olivier Gandrillon supervisor)
- Paul Lemarre, “Modélisation des souches de prions” (Laurent Pujo-Menjouet supervisor and Mostafa Adimy examiner).
- Olivier Gandrillon: PhD defense of Souad Zreika, La différenciation érythrocytaire : caractérisation moléculaire de l'engagement cellulaire, University of Lyon, examiner.
- Mostafa Adimy: PhD defense of Youssef Hbid, Modélisation et analyse prédictive des risques et des conséquences post accident vasculaire cérébral, Sorbonne université, reviewer.
- Mostafa Adimy: PhD defense of Karim Amin, Qualitative Analysis of Delay Differential Equations Modelling Tropical Diseases, Politehnica University of Bucharest, reviewer.
8 Scientific production
8.1 Publications of the year
International journals
Scientific book chapters
Doctoral dissertations and habilitation theses
Reports & preprints
8.2 Cited publications
- 36 articleStability Analysis of a Model of Interaction Between the Immune System and Cancer Cells in Chronic Myelogenous Leukemia.Bulletin of Mathematical Biology2017, 1--27
- 37 articleLong-term treatment effects in chronic myeloid leukemia.Journal of Mathematical Biology2017, 1-26
- 38 articleImplication of the Autologous Immune System in BCR-ABL Transcript Variations in Chronic Myelogenous Leukemia Patients Treated with Imatinib..Cancer Research7519October 2015, 4053-62
- 39 articleIdentification of Nascent Memory CD8 T Cells and Modeling of Their Ontogeny.Cell Systems43February 2017, 306-317
- 40 articleInferring gene regulatory networks from single-cell data: a mechanistic approach.BMC Systems Biology111November 2017, 105

