Keywords
Computer Science and Digital Science
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.2. Stochastic Modeling
- A6.1.4. Multiscale modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.2. Numerical probability
- A6.2.3. Probabilistic methods
- A6.3. Computation-data interaction
- A6.3.4. Model reduction
Other Research Topics and Application Domains
- B1. Life sciences
- B1.2. Neuroscience and cognitive science
- B1.2.1. Understanding and simulation of the brain and the nervous system
- B1.2.2. Cognitive science
1 Team members, visitors, external collaborators
Research Scientists
- Mathieu Desroches [Team leader, Inria, Researcher, HDR]
- Fabien Campillo [Inria, Senior Researcher, HDR]
- Pascal Chossat [CNRS, Emeritus, HDR]
- Olivier Faugeras [Inria, Emeritus, HDR]
- Maciej Krupa [Université Côte d'Azur, Senior Researcher, HDR]
- Simona Olmi [Inria, Starting Research Position, Jan 2021]
- Romain Veltz [Inria, Researcher, until Apr 2021]
Post-Doctoral Fellow
- Mattia Sensi [Inria, From 12/2021]
PhD Students
- Louisiane Lemaire [Inria]
- Yuri Rodrigues [Univ Côte d'Azur, until Jun 2021]
- Halgurd Taher [Inria]
Technical Staff
- Emre Baspinar [Inria, Engineer, until Mar 2021]
Interns and Apprentices
- Efstathios Pavlidis [Univ Côte d'Azur, from Mar 2021]
Administrative Assistant
- Marie-Cecile Lafont [Inria]
External Collaborators
- Daniele Avitabile [Université libre d'Amsterdam - Pays-Bas, until Nov 2021, HDR]
- Emre Baspinar [CNRS, from Apr 2021]
2 Overall objectives
MathNeuro focuses on the applications of multi-scale dynamics to neuroscience. This involves the modelling and analysis of systems with multiple time scales and space scales, as well as stochastic effects. We look both at single-cell models, microcircuits and large networks. In terms of neuroscience, we are mainly interested in questions related to synaptic plasticity and neuronal excitability, in particular in the context of pathological states such as epileptic seizures and neurodegenerative diseases such as Alzheimer.
Our work is quite mathematical but we make heavy use of computers for numerical experiments and simulations. We have close ties with several top groups in biological neuroscience. We are pursuing the idea that the "unreasonable effectiveness of mathematics" can be brought, as it has been in physics, to bear on neuroscience.
Modeling such assemblies of neurons and simulating their behavior involves putting together a mixture of the most recent results in neurophysiology with such advanced mathematical methods as dynamical systems theory, bifurcation theory, probability theory, stochastic calculus, theoretical physics and statistics, as well as the use of simulation tools.
We conduct research in the following main areas:
- Neural networks dynamics
- Mean-field and stochastic approaches
- Neural fields
- Slow-fast dynamics in neuronal models
- Modeling neuronal excitability
- Synaptic plasticity
- Memory processes
- Visual neuroscience
3 Research program
3.1 Neural networks dynamics
The study of neural networks is certainly motivated by the long term goal to understand how brain is working. But, beyond the comprehension of brain or even of simpler neural systems in less evolved animals, there is also the desire to exhibit general mechanisms or principles at work in the nervous system. One possible strategy is to propose mathematical models of neural activity, at different space and time scales, depending on the type of phenomena under consideration. However, beyond the mere proposal of new models, which can rapidly result in a plethora, there is also a need to understand some fundamental keys ruling the behaviour of neural networks, and, from this, to extract new ideas that can be tested in real experiments. Therefore, there is a need to make a thorough analysis of these models. An efficient approach, developed in our team, consists of analysing neural networks as dynamical systems. This allows to address several issues. A first, natural issue is to ask about the (generic) dynamics exhibited by the system when control parameters vary. This naturally leads to analyse the bifurcations 52 53 occurring in the network and which phenomenological parameters control these bifurcations. Another issue concerns the interplay between the neuron dynamics and the synaptic network structure.
3.2 Mean-field and stochastic approaches
Modeling neural activity at scales integrating the effect of thousands of neurons is of central importance for several reasons. First, most imaging techniques are not able to measure individual neuron activity (microscopic scale), but are instead measuring mesoscopic effects resulting from the activity of several hundreds to several hundreds of thousands of neurons. Second, anatomical data recorded in the cortex reveal the existence of structures, such as the cortical columns, with a diameter of about 50 to 1, containing of the order of one hundred to one hundred thousand neurons belonging to a few different species. The description of this collective dynamics requires models which are different from individual neurons models. In particular, when the number of neurons is large enough averaging effects appear, and the collective dynamics is well described by an effective mean-field, summarizing the effect of the interactions of a neuron with the other neurons, and depending on a few effective control parameters. This vision, inherited from statistical physics requires that the space scale be large enough to include a large number of microscopic components (here neurons) and small enough so that the region considered is homogeneous.
Our group is developing mathematical and numerical methods allowing on one hand to produce dynamic mean-field equations from the physiological characteristics of neural structure (neurons type, synapse type and anatomical connectivity between neurons populations), and on the other so simulate these equations; see Figure 1. These methods use tools from advanced probability theory such as the theory of Large Deviations 44 and the study of interacting diffusions 3.
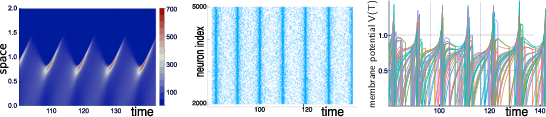
Simulations of the quasi-synchronous state of a stochastic neural network with N=5000N=5000 neurons.
3.3 Neural fields
Neural fields are a phenomenological way of describing the activity of population of neurons by delayed integro-differential equations. This continuous approximation turns out to be very useful to model large brain areas such as those involved in visual perception. The mathematical properties of these equations and their solutions are still imperfectly known, in particular in the presence of delays, different time scales and noise.
Our group is developing mathematical and numerical methods for analysing these equations. These methods are based upon techniques from mathematical functional analysis, bifurcation theory 20, 55, equivariant bifurcation analysis, delay equations, and stochastic partial differential equations. We have been able to characterize the solutions of these neural fields equations and their bifurcations, apply and expand the theory to account for such perceptual phenomena as edge, texture 38, and motion perception. We have also developed a theory of the delayed neural fields equations, in particular in the case of constant delays and propagation delays that must be taken into account when attempting to model large size cortical areas 21, 54. This theory is based on center manifold and normal forms ideas 19.
3.4 Slow-fast dynamics in neuronal models
Neuronal rhythms typically display many different timescales, therefore it is important to incorporate this slow-fast aspect in models. We are interested in this modeling paradigm where slow-fast point models, using Ordinary Differential Equations (ODEs), are investigated in terms of their bifurcation structure and the patterns of oscillatory solutions that they can produce. To insight into the dynamics of such systems, we use a mix of theoretical techniques — such as geometric desingularisation and centre manifold reduction 48 — and numerical methods such as pseudo-arclength continuation 42. We are interested in families of complex oscillations generated by both mathematical and biophysical models of neurons. In particular, so-called mixed-mode oscillations (MMOs)12, 40, 47, which represent an alternation between subthreshold and spiking behaviour, and bursting oscillations41, 46, also corresponding to experimentally observed behaviour 39; see Figure 2. We are working on extending these results to spatio-temporal neural models 2.
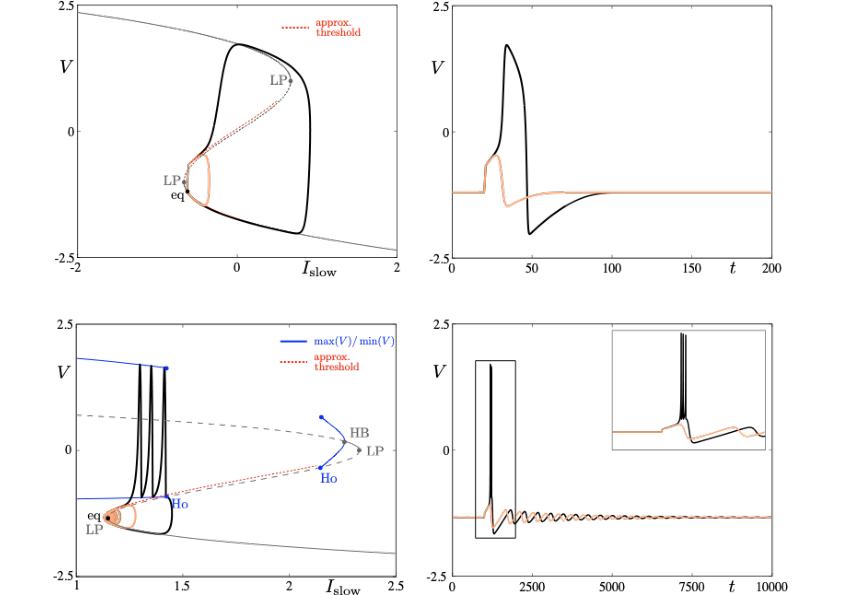
Excitability threshold as slow manifolds in a simple spiking model, namely the FitzHugh-Nagumo model, (top panels) and in a simple bursting model, namely the Hindmarsh-Rose model (bottom panels).
3.5 Modeling neuronal excitability
Excitability refers to the all-or-none property of neurons 43, 45. That is, the ability to respond nonlinearly to an input with a dramatic change of response from “none” — no response except a small perturbation that returns to equilibrium — to “all” — large response with the generation of an action potential or spike before the neuron returns to equilibrium. The return to equilibrium may also be an oscillatory motion of small amplitude; in this case, one speaks of resonator neurons as opposed to integrator neurons. The combination of a spike followed by subthreshold oscillations is then often referred to as mixed-mode oscillations (MMOs) 40. Slow-fast ODE models of dimension at least three are well capable of reproducing such complex neural oscillations. Part of our research expertise is to analyse the possible transitions between different complex oscillatory patterns of this sort upon input change and, in mathematical terms, this corresponds to understanding the bifurcation structure of the model. Furthermore, the shape of time series of this sort with a given oscillatory pattern can be analysed within the mathematical framework of dynamic bifurcations; see the section on slow-fast dynamics in Neuronal Models. The main example of abnormal neuronal excitability is hyperexcitability and it is important to understand the biological factors which lead to such excess of excitability and to identify (both in detailed biophysical models and reduced phenomenological ones) the mathematical structures leading to these anomalies. Hyperexcitability is one important trigger for pathological brain states related to various diseases such as chronic migraine 50, epilepsy 51 or even Alzheimer's Disease 49. A central central axis of research within our group is to revisit models of such pathological scenarios, in relation with a combination of advanced mathematical tools and in partnership with biological labs.
3.6 Synaptic Plasticity
Neural networks show amazing abilities to evolve and adapt, and to store and process information. These capabilities are mainly conditioned by plasticity mechanisms, and especially synaptic plasticity, inducing a mutual coupling between network structure and neuron dynamics. Synaptic plasticity occurs at many levels of organization and time scales in the nervous system 37. It is of course involved in memory and learning mechanisms, but it also alters excitability of brain areas and regulates behavioral states (e.g., transition between sleep and wakeful activity). Therefore, understanding the effects of synaptic plasticity on neurons dynamics is a crucial challenge.
Our group is developing mathematical and numerical methods to analyse this mutual interaction. On the one hand, we have shown that plasticity mechanisms 10, 17, Hebbian-like or STDP, have strong effects on neuron dynamics complexity, such as synaptic and propagation delays 21, dynamics complexity reduction, and spike statistics.
3.7 Memory processes
The processes by which memories are formed and stored in the brain are multiple and not yet fully understood. What is hypothesised so far is that memory formation is related to the activation of certain groups of neurons in the brain. Then, one important mechanism to store various memories is to associate certain groups of memory items with one another, which then corresponds to the joint activation of certain neurons within different subgroup of a given population. In this framework, plasticity is key to encode the storage of chains of memory items. Yet, there is no general mathematical framework to model the mechanism(s) behind these associative memory processes. We are aiming at developing such a framework using our expertise in multi-scale modelling, by combining the concepts of heteroclinic dynamics, slow-fast dynamics and stochastic dynamics.
The general objective that we wish to pursue in this project is to investigate non-equilibrium phenomena pertinent to storage and retrieval of sequences of learned items. In previous work by team members 9, 1, 15, it was shown that with a suitable formulation, heteroclinic dynamics combined with slow-fast analysis in neural field systems can play an organizing role in such processes, making the model accessible to a thorough mathematical analysis. Multiple choice in cognitive processes require a certain flexibility in the neural network, which has recently been investigated in the submitted paper 31.
Our goal is to contribute to identify general processes under which cognitive functions can be organized in the brain.
4 Application domains
The project underlying MathNeuro revolves around pillars of neuronal behaviour –excitability, plasticity, memory– in link with the initiation and propagation of pathological brain states in diseases such as cortical spreading depression (in link with certain forms of migraine with aura), epileptic seizures and Alzheimer’s Disease. Our work on memory processes can also potentially be applied to studying mental disorders such as schizophrenia or obsessive disorder troubles.
5 Highlights of the year
The first three PhD students of the EPI MathNeuro, Louisiane Lemaire, Yuri Rodrigues and Halgurd Taher, have all successfully defended their respective PhD in 2021. They all found postdoctoral positions, at Humbolt University (Berlin, Germany), the University of Sussex (Brighton, UK) and Charité Medical University (Berlin, Germany), respectively.
Simona Olmi, who held a Starting Research Position (SRP) in MathNeuro from 2018 to 2021, has obtained a permanent position as researcher in Computational Neuroscience at the National Research Council (CRN) in Florence, Italy.
6 New results
6.1 Neural Networks as dynamical systems
6.1.1 Patient-specific network connectivity combined with a next generation neural mass model to test clinical hypothesis of seizure propagation
Participants: Moritz Gerster [Institute for Theoretical Physics, Germany], Halgurd Taher [National Institute of Mental Heath, Czech Republic], Antonín Škoch [National Institute of Mental Heath, Czech Republic], Jaroslav Hlinka [National Institute of Mental Heath, Czech Republic], Maxime Guye [Centre de Résonance Magnétique Biologique et Médicale, France], Fabrice Bartolomei [Hôpital de la Timone, France], Viktor Jirsa [Institut de Neuroscience des Systèmes, France], Anna Zakharova [Institute for Theoretical Physics, Germany], Simona Olmi.
Dynamics underlying epileptic seizures span multiple scales in space and time, therefore understanding seizure mechanisms requires identifying the relations between seizure components within and across these scales, together with the analysis of their dynamical repertoire. In this view, mathematical models have been developed, ranging from single neuron to neural population. In this study, we consider a neural mass model able to exactly reproduce the dynamics of heterogeneous spiking neural networks. We combine mathematical modeling with structural information from non invasive brain imaging, thus building large-scale brain network models to explore emergent dynamics and test the clinical hypothesis. We provide a comprehensive study on the effect of external drives on neuronal networks exhibiting multistability, in order to investigate the role played by the neuroanatomical connectivity matrices in shaping the emergent dynamics. In particular, we systematically investigate the conditions under which the network displays a transition from a low activity regime to a high activity state, which we identify with a seizure-like event. This approach allows us to study the biophysical parameters and variables leading to multiple recruitment events at the network level. We further exploit topological network measures in order to explain the differences and the analogies among the subjects and their brain regions, in showing recruitment events at different parameter values. We demonstrate, along with the example of diffusion-weighted magnetic resonance imaging (dMRI) connectomes of 20 healthy subjects and 15 epileptic patients, that individual variations in structural connectivity, when linked with mathematical dynamic models, have the capacity to explain changes in spatiotemporal organization of brain dynamics, as observed in network-based brain disorders. In particular, for epileptic patients, by means of the integration of the clinical hypotheses on the epileptogenic zone (EZ), i.e., the local network where highly synchronous seizures originate, we have identified the sequence of recruitment events and discussed their links with the topological properties of the specific connectomes. The predictions made on the basis of the implemented set of exact mean-field equations turn out to be in line with the clinical pre-surgical evaluation on recruited secondary networks.This work has been published in Frontiers in Systems Neuroscience and is available as 27.
6.2 Mean field theory and stochastic processes
6.2.1 Cross-scale excitability in networks of quadratic integrate-and-fire neurons
Participants: Daniele Avitabile [VU Amsterdam, Netherlands, Inria MathNeuro], Mathieu Desroches [University of Pittsburgh, USA], G Bard Ermentrout [University of Pittsburgh, USA].
From the action potentials of neurons and cardiac cells to the amplification of calcium signals in oocytes, excitability is a hallmark of many biological signalling processes. In recent years, excitability in single cells has been related to multiple-timescale dynamics through canards, special solutions which determine the effective thresholds of the all-or-none responses. However, the emergence of excitability in large populations remains an open problem. Here, we show that the mechanisms of excitability in an infinite heterogeneous population of coupled quadratic integrate and fire (QIF) cells maintains echoes of the mechanism for the individual components. We exploit the Ott-Antonsen ansatz to derive low-dimensional dynamics for the coupled network and use it to describe the structure of canards via slow periodic forcing. We demonstrate that the thresholds for onset and offset of population firing can be found in the same way as those of the single cell. We combine theoretical and numerical analysis to develop a novel and comprehensive framework for excitability in large populations.This work has been submitted for publication and is available as 29.
6.2.2 Coherence resonance in neuronal populations: mean-field versus network model
Participants: Emre Baspinar [TU Berlin, Germany], Leonard Schülen [TU Berlin, Germany], Simona Olmi [TU Berlin, Germany], Anna Zakharova [TU Berlin, Germany].
The counter-intuitive phenomenon of coherence resonance describes a non-monotonic behavior of the regularity of noise-induced oscillations in the excitable regime, leading to an optimal response in terms of regularity of the excited oscillations for an intermediate noise intensity. We study this phenomenon in populations of FitzHugh-Nagumo (FHN) neurons with different coupling architectures. For networks of FHN systems in excitable regime, coherence resonance has been previously analyzed numerically. Here we focus on an analytical approach studying the mean-field limits of the locally and globally coupled populations. The mean-field limit refers to the averaged behavior of a complex network as the number of elements goes to infinity. We derive a mean-field limit approximating the locally coupled FHN network with low noise intensities. Further, we apply mean-field approach to the globally coupled FHN network. We compare the results of the mean-field and network frameworks for coherence resonance and find a good agreement in the globally coupled case, where the correspondence between the two approaches is sufficiently good to capture the emergence of anticoherence resonance. Finally, we study the effects of the coupling strength and noise intensity on coherence resonance for both the network and the mean-field model.This work has been published in Physical Review E and is available as 24.
6.2.3 The one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering
Participants: Samuel Nyobe [University of Yaoundé, Cameroun], Fabien Campillo [University of Yaoundé, Cameroun], Serge Moto [University of Yaoundé, Cameroun], Vivien Rossi [CIRAD].
Sequential Monte Carlo methods have been a major breakthrough in the field of numerical signal processing for stochastic dynamical state-space systems with partial and noisy observations. However, these methods still present certain weaknesses. One of the most fundamental is the degeneracy of the filter due to the impoverishment of the particles: the prediction step allows the particles to explore the state-space and can lead to the impoverishment of the particles if this exploration is poorly conducted or when it conflicts with the following observation that will be used in the evaluation of the likelihood of each particle. In this article, in order to improve this last step within the framework of the classic bootstrap particle filter, we propose a simple approximation of the one step fixed-lag smoother. At each time iteration, we propose to perform additional simulations during the prediction step in order to improve the likelihood of the selected particles.This work has been submitted for publication and is available as 32.
6.2.4 A stochastic model of hippocampal synaptic plasticity with geometrical readout of enzyme dynamics
Participants: Yuri Rodrigues [Cardiff University, UK], Cezar Tigaret [Cardiff University, UK], Hélène Marie [Institut de Pharmacologie Moléculaire et Cellulaire, France], Cian O'Donnell [University of Bristol, UK], Romain Veltz.
Discovering the rules of synaptic plasticity is an important step for understanding brain learning. Existing plasticity models are either 1) top-down and interpretable, but not flexible enough to account for experimental data, or 2) bottom-up and biologically realistic, but too intricate to interpret and hard to fit to data. We fill the gap between these approaches by uncovering a new plasticity rule based on a geometrical readout mechanism that flexibly maps synaptic enzyme dynamics to plasticity outcomes. We apply this readout to a multi-timescale model of hippocampal synaptic plasticity induction that includes electrical dynamics, calcium, CaMKII and calcineurin, and accurate representation of intrinsic noise sources. Using a single set of model parameters, we demonstrate the robustness of this plasticity rule by reproducing nine published ex vivo experiments covering various spike-timing and frequency-dependent plasticity induction protocols, animal ages, and experimental conditions. The model also predicts that in vivo-like spike timing irregularity strongly shapes plasticity outcome. This geometrical readout modelling approach can be readily applied to other excitatory or inhibitory synapses to discover their synaptic plasticity rules.This work has been submitted for publication and is available as 33.
6.2.5 Slow-fast dynamics in the mean-field limit of neural networks
Participants: Daniele Avitabile [VU Amsterdam, Inria MathNeuro], Emre Baspinar, Fabien Campillo, Mathieu Desroches, Olivier Faugeras.
In the context of the Human Brain Project (HBP, see section 5.1.1.1. below), we have recruited Emre Baspinar in December 2018 for a two-year postdoc, after which he stayed for a few more months on an engineer contract in order to complete some papers. Within MathNeuro, Emre has worked on analysing slow-fast dynamical behaviours in the mean-field limit of neural networks.In a first project, he has been analysing the slow-fast structure in the mean-field limit of a network of FitzHugh-Nagumo neuron models; the mean-field was previously established in 3 but its slow-fast aspect had not been analysed. In particular, he has proved a persistence result of Fenichel type for slow manifolds in this mean-field limit, thus extending previous work by Berglund et al. 36, 35. A manuscript is in preparation.
In a second project, he has been looking at a network of Wilson-Cowan systems whose mean-field limit is an ODE, and he has studied elliptic bursting dynamics in both the network and the limit: its slow-fast dissection, its singular limits and the role of canards. In passing, he has obtained a new characterisation of ellipting bursting via the construction of periodic limit sets using both the slow and the fast singular limits and unravelled a new singular-limit scenario giving rise to elliptic bursting via a new type of torus canard orbits. A manuscript has been published in Chaos and is available as 22 (see below).
6.2.6 Theoretical and Computational methods for Stochastic Differential Equations describing networks of Hopfield neurons
Participants: Olivier Faugeras [NJIT, USA], James MacLaurin [NJIT, USA], Etienne Tanré [Inria].
We investigate large networks of Hopfield neurons under various assumptions about the underlying network graphs (completely connected, sparsely connected, small world), the synaptic coefficients (Gaussian or non-Gaussian distributed, independent, correlated), and the neuronal populations present in the network (excitatory, inhibitory, balanced). These assumptions generate a large variety of different behaviours that we are trying to analyse mathematically and numerically. The mathematics include the description of the thermodynamics (meanfield) limit of these networks, when they exist, the type of solutions of the limit equations, their bifurcations with respect to changes of the network parameters, the fluctuations of the solutions to the network equations around the thermodynamics limit to understand the finite size effects. Along with these theoretical efforts, we are developing simulation tools in the Julia language with an eye on parallel implementations on GPUs to develop an intuition for the behaviours of these networks and guide the mathematical analysis.6.3 Neural fields theory
6.3.1 A cortical-inspired sub-Riemannian model for Poggendorff-type visual illusions
Participants: Emre Baspinar [Inria Morpheme], Luca Calatroni [Inria Morpheme], Valentina Franceschi [University of Padova, Italy], Dario Prandi [CNRS, Université Paris-Saclay, CentraleSupélec].
We consider Wilson-Cowan-type models for the mathematical description of orientation-dependent Poggendorff-like illusions. Our modelling improves two previously proposed cortical-inspired approaches, embedding the sub-Riemannian heat kernel into the neuronal interaction term, in agreement with the intrinsically anisotropic functional architecture of V1 based on both local and lateral connections. For the numerical realisation of both models, we consider standard gradient descent algorithms combined with Fourier-based approaches for the efficient computation of the sub-Laplacian evolution. Our numerical results show that the use of the sub-Riemannian kernel allows us to reproduce numerically visual misperceptions and inpainting-type biases in a stronger way in comparison with the previous approaches.This work has been published in Journal of Imaging and is available as 23.
6.4 Slow-fast dynamics in Neuroscience
6.4.1 Canonical models for torus canards in elliptic burster
Participants: Emre Baspinar [VU Amsterdam, Inria MathNeuro], Daniele Avitabile [VU Amsterdam, Inria MathNeuro], Mathieu Desroches.
We revisit elliptic bursting dynamics from the viewpoint of torus canard solutions. We show that at the transition to and from elliptic burstings, classical or mixed-type torus canards can appear, the difference between the two being the fast subsystem bifurcation that they approach, saddle-node of cycles for the former and subcritical Hopf for the latter. We first showcase such dynamics in a Wilson-Cowan type elliptic bursting model, then we consider minimal models for elliptic bursters in view of finding transitions to and from bursting solutions via both kinds of torus canards. We first consider the canonical model proposed by Izhikevich (ref. [22] in the manuscript) and adapted to elliptic bursting by Ju, Neiman, Shilnikov (ref. [24] in the manuscript), and we show that it does not produce mixed-type torus canards due to a nongeneric transition at one end of the bursting regime. We therefore introduce a perturbative term in the slow equation, which extends this canonical form to a new one that we call Leidenator and which supports the right transitions to and from elliptic bursting via classical and mixed-type torus canards, respectively. Throughout the study, we use singular flows () to predict the full system's dynamics ( small enough). We consider three singular flows: slow, fast and average slow, so as to appropriately construct singular orbits corresponding to all relevant dynamics pertaining to elliptic bursting and torus canards.This work has been published in Chaos and is available as 22.
6.4.2 Spike-adding and reset-induced canard cycles in adaptive integrate and fire models
Participants: Mathieu Desroches [University of Wrocław, Poland], Piotr Kowalczyk [University of Wrocław, Poland], Serafim Rodrigues [Basque Center for Applied Mathematics, Spain].
We study a class of planar integrate and fire models called adaptive integrate and fire (AIF) models, which possesses an adaptation variable on top of membrane potential, and whose subthreshold dynamics is piecewise linear . These AIF models therefore have two reset conditions, which enable bursting dynamics to emerge for suitable parameter values. Such models can be thought of as hybrid dynamical systems. We consider a particular slow dynamics within AIF models and prove the existence of bursting cycles with N resets, for any integer N. Furthermore, we study the transition between N- and (N + 1)-reset cycles upon vanishingly small parameter variations and prove (for N = 2) that such transitions are organised by canard cycles. Finally, using numerical continuation we compute branches of bursting cycles, including canard-explosive branches, in these AIF models, by suitably recasting the periodic problem as a two-point boundary-value problem.This work has been published in Nonlinear Dynamics and is available as 26.
6.4.3 Bursting in a next generation neural mass model with synaptic dynamics: a slow-fast approach
Participants: Halgurd Taher [VU Amsterdam, Netherlands, Inria MathNeuro], Daniele Avitabile [VU Amsterdam, Netherlands, Inria MathNeuro], Mathieu Desroches.
We report a detailed analysis on the emergence of bursting in a recently developed neural mass model that takes short-term synaptic plasticity into account. The one being used here is particularly important, as it represents an exact meanfield limit of synaptically coupled quadratic integrate & fire neurons, a canonical model for type I excitability. In absence of synaptic dynamics, a periodic external current with a slow frequency can lead to burst-like dynamics. The firing patterns can be understood using techniques of singular perturbation theory, specifically slow-fast dissection. In the model with synaptic dynamics the separation of timescales leads to a variety of slow-fast phenomena and their role for bursting is rendered inordinately more intricate. Canards are one of the main slow-fast elements on the route to bursting. They describe trajectories evolving nearby otherwise repelling locally invariant sets of the system and are found in the transition region from subthreshold dynamics to bursting. For values of the timescale separation nearby the singular limit , we report peculiar jump-on canards, which block a continuous transition to bursting. In the biologically more plausible regime of this transition becomes continuous and bursts emerge via consecutive spike-adding transitions. The onset of bursting is of complex nature and involves mixed-type like torus canards, which form the very first spikes of the burst and revolve nearby fast-subsystem repelling limit cycles. We provide numerical evidence for the same mechanisms to be responsible for the emergence of bursting in the quadratic integrate & fire network with plastic synapses. The main conclusions apply for the network, owing to the exactness of the meanfield limit.This work has been submitted for publication and is available as 34.
6.5 Mathematical modeling of neuronal excitability
6.5.1 Initiation of migraine-related cortical spreading depolarization by hyperactivity of GABAergic neurons and NaV1.1 channels
Participants: Oana Chever [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Sarah Zerimeh [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Paolo Scalmani [Foundation IRCCS Neurological Institute Carlo Besta, Milan, Italy], Louisiane Lemaire [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Lara Pizzamiglio [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Alexandre Loucif [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Marion Ayrault [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Martin Krupa [LJAD, Inria MathNeuro], Mathieu Desroches [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Fabrice Duprat [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Isabelle Léna [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Sandrine Cestèle [IPMC, Sophia Antipolis et Université Côte d'Azur, France], Massimo Mantegazza [IPMC, Sophia Antipolis, Université Côte d'Azur et INSERM, France].
Spreading depolarizations (SDs) are involved in migraine, epilepsy, stroke, traumatic brain injury, and subarachnoid hemorrhage. However, the cellular origin and specific differential mechanisms are not clear. Increased glutamatergic activity is thought to be the key factor for generating cortical spreading depression (CSD), a pathological mechanism of migraine. Here, we show that acute pharmacological activation of (the main Na channel of interneurons) or optogenetic-induced hyperactivity of GABAergic interneurons is sufficient to ignite CSD in the neocortex by spiking-generated extracellular K build-up. Neither GABAergic nor glutamatergic synaptic transmission were required for CSD initiation. CSD was not generated in other brain areas, suggesting that this is a neocortex-specific mechanism of CSD initiation. Gain-of-function mutations of (SCN1A) cause familial hemiplegic migraine type-3 (FHM3), a subtype of migraine with aura, of which CSD is the neurophysiological correlate. Our results provide the mechanism linking gain of function to CSD generation in FHM3. Thus, we reveal the key role of hyperactivity of GABAergic interneurons in a mechanism of CSD initiation, which is relevant as a pathological mechanism of Nav1.1 FHM3 mutations, and possibly also for other types of migraine and diseases in which SDs are involved.This work has been published in Journal of Clinical Investigation and is available as 25.
The extension of this work is the topic of the PhD of Louisiane Lemaire, who started in October 2018 and was successfully defended in December 2021. A first part of Louisiane's PhD has been to improve and extend the model published in 11 in a number of ways: replace the GABAergic neuron model used in 11, namely the Wang-Buszáki model, by a more recent fast-spiking cortical interneuron model due to Golomb and collaborators; implement the effect of the HM1a toxin used by M. Mantegazza to mimic the genetic mutation of sodium channels responsible for the hyperactivity of the GABAergic neurons; take into account ionic concentration dynamics (relaxing the hypothesis of constant reversal potentials) for the GABAergic as well whereas in 11 this was done only for the Pyramidal neuron. Furthermore, another mutation of this sodium channel leads to hyperactivity of the pyramidal neurons in a way that is akin to epileptiform activity. The model by Louisiane Lemaire has been extended in order to account for this pathological scenario as well. This required a great deal of modelling and calibration and the simulation results are closer to the actual experiments by Mantegazza than in our previous study. An article has been published (28, see below).
6.5.2 Modeling NaV1.1/SCN1A sodium channel mutations in a microcircuit with realistic ion concentration dynamics suggests differential GABAergic mechanisms leading to hyperexcitability in epilepsy and hemiplegic migraine
Participants: Louisiane Lemaire [LJAD, Inria MathNeuro], Martin Krupa [LJAD, Inria MathNeuro], Mathieu Desroches [IPMC, Sophia Antipolis, Université Côte d'Azur et INSERM, France], Lara Pizzamiglio [IPMC, Sophia Antipolis, Université Côte d'Azur et INSERM, France], Paolo Scalmani [Foundation IRCCS Neurological Institute Carlo Besta, Milan, Italy], Massimo Mantegazza [IPMC, Sophia Antipolis, Université Côte d'Azur et INSERM, France].
Loss of function mutations of SCN1A, the gene coding for the voltage-gated sodium channel , cause different types of epilepsy, whereas gain of function mutations cause sporadic and familial hemiplegic migraine type 3 (FHM-3). However, it is not clear yet how these opposite effects can induce paroxysmal pathological activities involving neuronal networks’ hyperexcitability that are specific of epilepsy (seizures) or migraine (cortical spreading depolarization, CSD). To better understand differential mechanisms leading to the initiation of these pathological activities, we used a two-neuron conductance-based model of interconnected GABAergic and pyramidal glutamatergic neurons, in which we incorporated ionic concentration dynamics in both neurons. We modeled FHM-3 mutations by increasing the persistent sodium current in the interneuron and epileptogenic mutations by decreasing the sodium conductance in the interneuron. Therefore, we studied both FHM-3 and epileptogenic mutations within the same framework, modifying only two parameters. In our model, the key effect of gain of function FHM-3 mutations is ion fluxes modification at each action potential (in particular the larger activation of voltage-gated potassium channels induced by the NaV1.1 gain of function), and the resulting CSD-triggering extracellular potassium accumulation, which is not caused only by modifications of firing frequency. Loss of function epileptogenic mutations, on the other hand, increase GABAergic neurons’ susceptibility to depolarization block, without major modifications of firing frequency before it. Our modeling results connect qualitatively to experimental data: potassium accumulation in the case of FHM-3 mutations and facilitated depolarization block of the GABAergic neuron in the case of epileptogenic mutations. Both these effects can lead to pyramidal neuron hyperexcitability, inducing in the migraine condition depolarization block of both the GABAergic and the pyramidal neuron. Overall, our findings suggest different mechanisms of network hyperexcitability for migraine and epileptogenic mutations, implying that the modifications of firing frequency may not be the only relevant pathological mechanism.This work has been published in PLoS Computational Biology and is available as 28.
6.5.3 Mathematical modeling of the neurotransmitter cycle, in link with neuronal excitability and plasticity in both healthy and pathological states
Participants: Afia B Ali [School of Pharmacy, University College London, UK], Mathieu Desroches, Serafim Rodrigues, Mattia Sensi.
The project is part of a long-standing collaboration between Mathieu Desroches (MathNeuro Project-Team, Inria) and Serafim Rodrigues (MCEN research group, Basque Center for Applied Mathematics, Bilbao, Spain) on neurotransmission and its possible disruptions 17 (see also 10). Matti Sensi has been recruited as postdoc in MathNeuro at the end of 2021 to work on this project. The work will be organised around a modeling project on multi-timescale aspects of synaptic transmission, which can be synchronous, asynchronous or spontaneous. Building on our already- existing modeling platform, we will focus on two main extensions: the endocytotic part of the neurotransmitter cycle, and the integration of glial activity into the model. This project is also related to the NeuroTransSF associated team between MathNeuro and MCEN, and the extended model will be used (within a time horizon that goes beyond the postdoc of Mattia Sensi) in the context of experiments performed by Afia Ali on early effects of Alzheimer's Disease.6.6 Mathematical modeling of memory processes
6.6.1 Dynamic branching in a neural network model for probabilistic prediction of sequences
Participants: Elif Köksal Ersöz [INSERM, Rennes], Pascal Chossat [CNRS and Inria MathNeuro], Martin Krupa [LJAD and Inria MathNeuro], Frédéric Lavigne [BCL, Université Côte d'Azur].
An important function of the brain is to adapt behavior by selecting between different predictions of sequences of stimuli likely to occur in the environment. The present research studied the branching behavior of a computational network model of populations of excitatory and inhibitory neurons, both analytically and through simulations. Results show how synaptic efficacy, retroactive inhibition and short-term synaptic depression determine the dynamics of choices between different predictions of sequences having different probabilities. Further results show that changes in the probability of the different predictions depend on variations of neuronal gain. Such variations allow the network to optimize the probability of its predictions to changing probabilities of the sequences without changing synaptic efficacy.This work has been submitted for publication and is available as 31.
6.7 Modelling the visual system
6.7.1 Spatial and color hallucinations in a mathematical model of primary visual cortex
Participants: Olivier Faugeras [Imperial College London, UK], Anna Song [Imperial College London, UK], Romain Veltz.
We study a simplified model of the representation of colors in the primate primary cortical visual area V1. The model is described by an initial value problem related to a Hammerstein equation. The solutions to this problem represent the variation of the activity of populations of neurons in V1 as a function of space and color. The two space variables describe the spatial extent of the cortex while the two color variables describe the hue and the saturation represented at every location in the cortex. We prove the well-posedness of the initial value problem. We focus on its stationary, i.e. independent of time, and periodic in space solutions. We show that the model equation is equivariant with respect to the direct product G of the group of the Euclidean transformations of the planar lattice determined by the spatial periodicity and the group of color transformations, isomorphic to , and study the equivariant bifurcations of its stationary solutions when some parameters in the model vary. Their variations may be caused by the consumption of drugs and the bifurcated solutions may represent visual hallucinations in space and color. Some of the bifurcated solutions can be determined by applying the Equivariant Branching Lemma (EBL) by determining the axial subgroups of G. These define bifurcated solutions which are invariant under the action of the corresponding axial subgroup. We compute analytically these solutions and illustrate them as color images. Using advanced methods of numerical bifurcation analysis we then explore the persistence and stability of these solutions when varying some parameters in the model. We conjecture that we can rely on the EBL to predict the existence of patterns that survive in large parameter domains but not to predict their stability. On our way we discover the existence of spatially localized stable patterns through the phenomenon of "snaking".This work has been accepted for publication in the "Comptes Rendus Mathématique" and is available as 30.
7 Partnerships and cooperations
Participants: Fabien Campillo [co-tutelle PhD Student, BCAM, Spain and Inria MathNeuro], Mathieu Desroches [co-tutelle PhD Student, BCAM, Spain and Inria MathNeuro], Guillaume Girier [co-tutelle PhD Student, BCAM, Spain and Inria MathNeuro], Serafim Rodrigues [ikerbasque & BCAM, Spain].
7.1 International initiatives
7.1.1 Inria associated team not involved in an IIL or an international program
NeuroTransSF
-
Title:
NeuroTransmitter cycle: A Slow-Fast modeling approach
-
Duration:
from 2019 to 2022
-
Coordinator:
Serafim Rodrigues (srodrigues@bcamath.org)
-
Partners:
Basque Center for Applied Mathematics (BCAM, Bilbao, Spain)
-
Inria contact:
Mathieu Desroches
-
Summary:
This associated team project proposes to deepen the links between two young research groups, on strong Neuroscience thematics. This project aims to start from a joint work in which we could successfully model synaptic transmission delays for both excitatory and inhibitory synapses, matching experimental data, and to supplant it in two distinct directions. On the one hand, by modeling the endocytosis so as to obtain a complete mathematical formulation of the presynaptic neurotransmitter cycle, which will then be integrated within diverse neuron models (in particular interneurons) hence allowing a refined analysis of their excitability and short-term plasticity properties. On the other hand, by modeling the postsynaptic neurotransmitter cycle in link with long-term plasticity and memory. We will incorporate these new models of synapse in different types of neuronal networks and we will then study their excitability, plasticity and synchronization properties in comparison with classical models. This project will benefit from strong experimental collaborations (UCL, Alicante) and it is coupled to the study of brain pathologies linked with synaptic dysfunctions, in particular certain early signs of Alzheimer’s Disease. Our initiative also contains a training aspect with two PhD student involved as well as a series of mini-courses which we will propose to the partner institute on this research topic; we will also organize a "wrap-up" workshop in Sophia at the end of it. Finally, the project is embedded within a strategic tightening of our links with Spain with the objective of pushing towards the creation of a Southern-Europe network for Mathematical, Computational and Experimental Neuroscience, which will serve as a stepping stone in order to extend our influence beyond Europe. The web page of the associated team is here. It contains the latest developments and new collaborations that have emerged from this project.
7.2 International research visitors
7.2.1 Visits of international scientists
Other international visits to the team
Ernest Montbrió
-
Status
(Associate Professor)
-
Institution of origin:
Universitat Pompeu Fabra, Barcelona
-
Country:
Spain
-
Dates:
8-10 December 2021
-
Context of the visit:
He visited to participate to the thesis jury of Halgurd Taher (he was one of the reviewers of the thesis) as well as to initiate a research collaboration with Mathieu Desroches.
-
Mobility program/type of mobility:
research stay
7.2.2 Visits to international teams
Research stays abroad
Mathieu Desroches
-
Visited institution:
BCAM, Bilbao
-
Country:
Spain
-
Dates:
16-25 October 2021
-
Context of the visit:
Collaboration with S. Rodrigues on the associated team NeuroTransSF project.
-
Mobility program/type of mobility:
research stay
7.3 European initiatives
7.3.1 FP7 & H2020 projects
Human Brain Project (HBP)
-
Title:
Human Brain Project Specific Grant Agreement 3
-
Duration:
3 years (March 2020 - March 2023)
-
Coordinator:
EPFL
-
Partners:
See the web page of the project. Olivier Faugeras is leading the task T4.1.3 entitled “Meanfield and population models” of the Worpackage W4.1 “Bridging Scales”.
-
Summary:
Understanding the human brain is one of the greatest challenges facing 21st century science. If we can rise to the challenge, we can gain profound insights into what makes us human, develop new treatments for brain diseases and build revolutionary new computing technologies. Today, for the first time, modern ICT has brought these goals within sight. The goal of the Human Brain Project, part of the FET Flagship Programme, is to translate this vision into reality, using ICT as a catalyst for a global collaborative effort to understand the human brain and its diseases and ultimately to emulate its computational capabilities. The Human Brain Project will last ten years and will consist of a ramp-up phase (from month 1 to month 36) and subsequent operational phases. This Grant Agreement covers the ramp-up phase. During this phase the strategic goals of the project will be to design, develop and deploy the first versions of six ICT platforms dedicated to Neuroinformatics, Brain Simulation, High Performance Computing, Medical Informatics, Neuromorphic Computing and Neurorobotics, and create a user community of research groups from within and outside the HBP, set up a European Institute for Theoretical Neuroscience, complete a set of pilot projects providing a first demonstration of the scientific value of the platforms and the Institute, develop the scientific and technological capabilities required by future versions of the platforms, implement a policy of Responsible Innovation, and a programme of transdisciplinary education, and develop a framework for collaboration that links the partners under strong scien- tific leadership and professional project management, providing a coherent European approach and ensuring effective alignment of regional, national and European research and programmes. The project work plan is organized in the form of thirteen subprojects, each dedicated to a specific area of activity. A significant part of the budget will be used for competitive calls to complement the collective skills of the Consortium with additional expertise.
8 Dissemination
8.1 Promoting scientific activities
8.1.1 Scientific events: organisation
General chair, scientific chair
-
Fabien Campillo
is a founding member of the African scholarly Society on Digital Sciences (ASDS).
Member of the organizing committees
-
Mathieu Desroches
was a member of the organizing committee of the international conference “Dynamics Days Europe” 2021, held in Nice on 23-27 August 2021.
-
Louisiane Lemaire
was a member of the local organizing committee of the international conference “Dynamics Days Europe” 2021, held in Nice on 23-27 August 2021.
- Louisiane Lemaire
-
Halgurd Taher
was a member of the local organizing committee of the international conference “Dynamics Days Europe” 2021, held in Nice on 23-27 August 2021.
- Halgurd Taher
8.1.2 Journal
Member of the editorial boards
-
Mathieu Desroches
is Review Editor of the journal Frontiers in Physiology (ImpactFactor 3.4).
-
Olivier Faugeras
is founder and editor-in-chief of the journal Mathematical Neuroscience and Applications, under the diamond model (no charges for authors and readers) supported by Episciences.
Reviewer - reviewing activities
-
Fabien Campillo
acted as a reviewer for the Journal of Mathematical Biology.
-
Mathieu Desroches
acted as a reviewer for the journals SIAM Journal on Applied Dynamical Systems (SIADS), Journal of Mathematical Biology, PLoS Computational Biology, Journal of Nonlinear Science, Nonlinear Dynamics, Physica D, Applied Mathematics Modelling, Journal of the European Mathematical Society.
-
Martin Krupa
acted as a reviewer for Proceedings of the National Academy of Sciences of the USA and SIAM Journal on Applied Dynamical Systems (SIADS).
8.1.3 Invited talks
-
Mathieu Desroches
gave a webinar talk entitled "Canards in neural networks and their mean-field limits" at the Lowlands dynamics Seminar of VU Amsterdam, 25 November 2021
-
Louisiane Lemaire
gave a webinar talk entitled "Mathematical Model of the Mutations of a Sodium Channel (NaV1.1) Capturing Both Migraine and Epilepsy Scenarios" at the SIAM Conference on Applications of Dynamical Systems (DS21), 27 May 2021.
-
Louisiane Lemaire
gave a webinar talk entitled "Mathematical Model of the Mutations of a Sodium Channel (NaV1.1) Capturing Both Migraine and Epilepsy Scenarios" at
-
-the virtual Society for Mathematical Biology annual meeting (SMB21), 14 June 2021;
-
-the 2021 International Conference on Mathematical Neuroscience - Digital Edition, 28 June 2021;
-
-the International Conference on Spreading Depolarization, 21 September 2021.
-
-
-
Halgurd Taher
gave a webinar talk entitled "Emergence of Bursting and Slow-Fast Phenomena in a Next Generation Neural Mass Model with Short-Term Synaptic Plasticity" at the SIAM Conference on Applications of Dynamical Systems (DS21), 27 May 2021.
-
Halgurd Taher
gave a webinar talk entitled "Bursting in a next generation neural mass model with synaptic dynamics: a slow-fast approach" at the virtual Society for Mathematical Biology annual meeting (SMB21), 15 June 2021.
-
Halgurd Taher
gave a webinar talk entitled "Exact neural mass model for synaptic-based working memory" at
-
-the 2021 International Conference on Mathematical Neuroscience - Digital Edition, 28 June 2021;
-
-the 2021 CNS conference, 7 July 2021;
-
-the Dynamics Days Europe 2021 Conference, 27 August 2021;
-
-the Bernstein Conference, 22 September 2021.
-
-
8.1.4 Leadership within the scientific community
-
Fabien Campillo
was member of the local committee in charge of the scientific selection of visiting scientists (Comité NICE).
-
Mathieu Desroches
was on the Scientific Committee of the Complex Systems Academy of the UCA JEDI Idex.
8.2 Teaching - Supervision - Juries
8.2.1 Teaching
-
Master:
Emre Baspinar, Dynamical Systems in the context of neuron models, (Lectures, example classes and computer labs), 6 hours (Jan. 2021), M1 (Mod4NeuCog), Université Côte d'Azur, Sophia Antipolis, France.
-
Master:
Mathieu Desroches, Modèles Mathématiques et Computationnels en Neuroscience (Lectures, example classes and computer labs), 12 hours (Feb. 2021), M1 (BIM), Sorbonne Université, Paris, France.
-
Master:
Mathieu Desroches, Dynamical Systems in the context of neuron models, (Lectures, example classes and computer labs), 6 hours (Jan. 2021) and 9 hours (Nov.-Dec. 2021), M1 (Mod4NeuCog), Université Côte d'Azur, Sophia Antipolis, France.
-
Master:
Louisiane Lemaire, Modèles Mathématiques et Computationnels en Neuroscience (example classes and computer labs), 6 hours (Feb 2021), M1 (BIM), Sorbonne Université, Paris, France.
8.2.2 Supervision
-
PhD completed:
Louisiane Lemaire, “Multi-scale mathematical modeling of cortical spreading depression”, co-supervised by Mathieu Desroches and Martin Krupa, was successfully defended on 13 December 2021.
-
PhD completed:
Yuri Rodrigues, "Unifying experimental heterogeneity in a geometrical synaptic plasticity model”, co-supervised by Romain Veltz and Hélène Marie (IPMC, Sophia Antipolis), was successfully defended on 30 June 2021.
-
PhD completed:
Halgurd Taher, "Next generation neural mass models: working memory, all-brain modelling and multi-timescale phenomena", co-supervised by Mathieu Desroches and Simona Olmi, was successfully defended on 9 December 2021.
-
Master 1 internship:
Efstathios Pavlidis, "Analysis of Mixed Mode Oscillations using multiple time-scale dynamics: two case studies", co-supervised by Emre Baspinar, Mathieu Desroches and Martin Krupa, April-May 2020.
-
Master 2 internship:
Efstathios Pavlidis, "Multiple-timescale dynamics and mixed states in a model of Bipolar Disorder", supervised by Mathieu Desroches, September 2021 - February 2022.
8.2.3 Juries
-
Mathieu Desroches
was member of the jury and reviewer of the PhD of Mattia Sensi entitled "A Geometric Singular Perturbation approach to epidemic compartmental models", supervised by Andrea Pugliese, University of Trento (Italy), 18 January 2021.
-
Mathieu Desroches
was member of the jury of the PhD of Lou Zonca entitled "Modeling and analytical computations of burst and interburst dynamics in neuronal networks, applications to neuron-glia interactions and oscillatory brain rhythms", supervised by David Holcman, ENS Paris, 16 July 2021.
9 Scientific production
9.1 Major publications
- 1 articleLatching dynamics in neural networks with synaptic depression.PLoS ONE128August 2017, e0183710
- 2 articleSpatiotemporal canards in neural field equations.Physical Review E 954April 2017, 042205
- 3 articleMean-field description and propagation of chaos in networks of Hodgkin-Huxley neurons.The Journal of Mathematical Neuroscience21We derive the mean-field equations arising as the limit of a network of interacting spiking neurons, as the number of neurons goes to infinity. The neurons belong to a fixed number of populations and are represented either by the Hodgkin-Huxley model or by one of its simplified version, the FitzHugh-Nagumo model. The synapses between neurons are either electrical or chemical. The network is assumed to be fully connected. The maximum conductances vary randomly. Under the condition that all neurons~ initial conditions are drawn independently from the same law that depends only on the population they belong to, we prove that a propagation of chaos phenomenon takes place, namely that in the mean-field limit, any finite number of neurons become independent and, within each population, have the same probability distribution. This probability distribution is a solution of a set of implicit equations, either nonlinear stochastic differential equations resembling the McKean-Vlasov equations or non-local partial differential equations resembling the McKean-Vlasov-Fokker-Planck equations. We prove the wellposedness of the McKean-Vlasov equations, i.e. the existence and uniqueness of a solution. We also show the results of some numerical experiments that indicate that the mean-field equations are a good representation of the mean activity of a finite size network, even for modest sizes. These experiments also indicate that the McKean-Vlasov-Fokker-Planck equations may be a good way to understand the mean-field dynamics through, e.g. a bifurcation analysis.2012, URL: http://www.mathematical-neuroscience.com/content/2/1/10
- 4 articleA sub-Riemannian model of the visual cortex with frequency and phase.The Journal of Mathematical Neuroscience101December 2020
- 5 articleLinks between deterministic and stochastic approaches for invasion in growth-fragmentation-death models.Journal of mathematical biology736-72016, 1781--1821URL: https://hal.science/hal-01205467
- 6 articleWeak convergence of a mass-structured individual-based model.Applied Mathematics & Optimization7212015, 37--73URL: https://hal.inria.fr/hal-01090727
- 7 articleAnalysis and approximation of a stochastic growth model with extinction.Methodology and Computing in Applied Probability1822016, 499--515URL: https://hal.science/hal-01817824
- 8 articleEffect of population size in a predator--prey model.Ecological Modelling2462012, 1--10URL: https://hal.inria.fr/hal-00723793
- 9 articleHeteroclinic cycles in Hopfield networks.Journal of Nonlinear ScienceJanuary 2016
- 10 articleShort-term synaptic plasticity in the deterministic Tsodyks-Markram model leads to unpredictable network dynamics.Proceedings of the National Academy of Sciences of the United States of America 110412013, 16610-16615
- 11 articleModeling cortical spreading depression induced by the hyperactivity of interneurons.Journal of Computational NeuroscienceOctober 2019
- 12 articleCanards, folded nodes and mixed-mode oscillations in piecewise-linear slow-fast systems.SIAM Review584accepted for publication in SIAM Review on 13 August 2015November 2016, 653-691
- 13 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster.Chaos234October 2013, 046106
- 14 articleHopf bifurcation in a nonlocal nonlinear transport equation stemming from stochastic neural dynamics.ChaosFebruary 2017
- 15 articleNeuronal mechanisms for sequential activation of memory items: Dynamics and reliability.PLoS ONE1542020, 1-28
- 16 unpublishedCanard-induced complex oscillations in an excitatory network.November 2018, working paper or preprint
- 17 articleTime-coded neurotransmitter release at excitatory and inhibitory synapses.Proceedings of the National Academy of Sciences of the United States of America 1138February 2016, E1108-E1115
- 18 unpublishedA new twist for the simulation of hybrid systems using the true jump method.December 2015, working paper or preprint
- 19 articleA Center Manifold Result for Delayed Neural Fields Equations.SIAM Journal on Mathematical Analysis4532013, 1527-1562
- 20 articleA center manifold result for delayed neural fields equations.SIAM Journal on Applied Mathematics (under revision)RR-8020July 2012
- 21 articleInterplay Between Synaptic Delays and Propagation Delays in Neural Field Equations.SIAM Journal on Applied Dynamical Systems1232013, 1566-1612
9.2 Publications of the year
International journals
Reports & preprints
9.3 Cited publications
- 35 articleHunting French ducks in a noisy environment.Journal of Differential Equations25292012, 4786--4841
- 36 bookNoise-induced phenomena in slow-fast dynamical systems: a sample-paths approach.Springer Science & Business Media2006
- 37 articleTheory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex.The Journal of Neuroscience211982, 32--48
- 38 articleHyperbolic planforms in relation to visual edges and textures perception.PLoS Computational Biology5122009, e1000625
- 39 articleA role for fast rhythmic bursting neurons in cortical gamma oscillations in vitro.Proceedings of the National Academy of Sciences of the United States of America101182004, 7152--7157
- 40 articleMixed-Mode Oscillations with Multiple Time Scales.SIAM Review542May 2012, 211-288
- 41 articleMixed-Mode Bursting Oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster.Chaos234October 2013, 046106
- 42 articleThe geometry of slow manifolds near a folded node.SIAM Journal on Applied Dynamical Systems742008, 1131--1162
- 43 bookMathematical foundations of neuroscience.35Springer2010
- 44 articleA large deviation principle and an expression of the rate function for a discrete stationary gaussian process.Entropy16122014, 6722--6738
- 45 bookDynamical systems in neuroscience.MIT press2007
- 46 articleNeural excitability, spiking and bursting.International Journal of Bifurcation and Chaos10062000, 1171--1266
- 47 articleMixed-mode oscillations in a three time-scale model for the dopaminergic neuron.Chaos: An Interdisciplinary Journal of Nonlinear Science1812008, 015106
- 48 articleRelaxation oscillation and canard explosion.Journal of Differential Equations17422001, 312--368
- 49 articleAmyloid precursor protein: from synaptic plasticity to Alzheimer's disease.Annals of the New York Academy of Sciences104812005, 149--165
- 50 articlePathophysiology of migraine.Annual review of physiology752013, 365--391
- 51 articleDynamical diseases of brain systems: different routes to epileptic seizures.IEEE transactions on biomedical engineering5052003, 540--548
- 52 articleA Markovian event-based framework for stochastic spiking neural networks.Journal of Computational Neuroscience30April 2011
- 53 articleNeural Mass Activity, Bifurcations, and Epilepsy.Neural Computation2312December 2011, 3232--3286
- 54 articleA Center Manifold Result for Delayed Neural Fields Equations.SIAM Journal on Mathematical Analysis4532013, 1527-562
- 55 articleLocal/Global Analysis of the Stationary Solutions of Some Neural Field Equations.SIAM Journal on Applied Dynamical Systems93August 2010, 954--998URL: http://arxiv.org/abs/0910.2247

