Keywords
Computer Science and Digital Science
- A2.1.3. Object-oriented programming
- A2.1.4. Functional programming
- A2.4.3. Proofs
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.5. Numerical Linear Algebra
- A6.2.8. Computational geometry and meshes
- A6.3.1. Inverse problems
- A6.3.4. Model reduction
- A6.3.5. Uncertainty Quantification
Other Research Topics and Application Domains
- B3.1. Sustainable development
- B3.3.1. Earth and subsoil
- B3.4.2. Industrial risks and waste
- B3.4.3. Pollution
- B4.1. Fossile energy production (oil, gas)
- B4.2.1. Fission
- B5.5. Materials
1 Team members, visitors, external collaborators
Research Scientists
- Martin Vohralík [Team leader, Inria, Senior Researcher, HDR]
- François Clément [Inria, Researcher]
- Zhaonan Dong [Inria, Researcher]
- Alexandre Ern [École Nationale des Ponts et Chaussées, Senior Researcher]
- Jean Luc Guermond [Inria, Advanced Research Position, Aug 2021, HDR]
- Michel Kern [Inria, Researcher]
- Géraldine Pichot [Inria, Researcher]
Post-Doctoral Fellows
- Manuela Bastidas Olivares [Inria, from Oct 2021]
- Andre Harnist [Inria, from Nov 2021]
- Koondanibha Mitra [Inria, Jan 2021]
PhD Students
- Joelle Ferzly [IFPEN]
- Ani Miraci [Inria, Jan 2021]
- Romain Mottier [CEA, From Nov 2021]
- Houda Mouhcine [Inria, From Oct 2021]
- Idrissa Niakh [EDF]
- Stefano Piccardo [École Nationale des Ponts et Chaussées]
- Ari Rappaport [Inria]
- Morgane Steins [CEA]
- Daniel Zegarra Vasquez [Inria, from Oct 2021]
Technical Staff
- Sebastien Furic [Inria, Engineer, from Apr 2021]
- Simon Legrand [Inria, Engineer]
Interns and Apprentices
- Louise Leclerc [ENS, Intern, From Jun to Jul 2021]
- Houda Mouhcine [Inria, Intern, From Apr to Sep 2021]
- Zuodong Wang [Inria, from Jun 2021 until Sep 2021]
- Daniel Zegarra Vasquez [Inria, from Apr 2021 until Sep 2021]
Administrative Assistant
- Derya Gök [Inria, until Nov 2021]
Visiting Scientists
- Théophile Chaumont-Frelet [Inria Sophia Antipolis, from Jun until Jul and Dec 2021]
- Omar Duran [University of Bergen - Norway, from Oct 2021 until Nov 2021]
- Moritz Hauck [University of Augsburg - Germany, November 2021]
- Roland Maier [University of Jena - Germany, November 2021]
- Frédéric Marazzato [Université d'État de Louisiane - USA, from Jul 2021 until Sep 2021]
- Lorenzo Mascotto [University of Milano-Bicocca - Italy, From Jun to Jul 2021]
- Dimitra Plaka [National Technique University of Athens - Greece, October 2021]
- Rolf Stenberg [Aalto University - Finland, Sep 2021]
External Collaborators
- Guy Chavent [NC]
- François Delebecque [NC]
- Jérôme Jaffré [NC, HDR]
- Caroline Japhet [Université Paris-Nord]
- Kenan Kergrene-Profit [Université de technologie de Compiègne]
- Vincent Martin [Université de technologie de Compiègne]
- Jean-Elizabeth Roberts [NC, HDR]
- Pierre Weis [NC]
2 Overall objectives
The project-team SERENA is concerned with numerical methods for environmental problems. The main topics are the conception and analysis of models based on partial differential equations, the study of their precise and efficient numerical approximation, and implementation issues with special concern for reliability and correctness of programs. We are in particular interested in guaranteeing the quality of the overall simulation process. SERENA has taken over the project-team POMDAPI2 which ended on May 31, 2015. It has been given an authorization to become a joint project-team between INRIA and ENPC at the Committee of Projects, September 1st, 2016, and was created as project-team on April 10, 2017.
3 Research program
3.1 Multiphysics coupling
Within our project, we start from the conception and analysis of models based on partial differential equations (PDEs). Already at the PDE level, we address the question of coupling of different models; examples are that of simultaneous fluid flow in a discrete network of two-dimensional fractures and in the surrounding three-dimensional porous medium, or that of interaction of a compressible flow with the surrounding elastic deformable structure. The key physical characteristics need to be captured, whereas existence, uniqueness, and continuous dependence on the data are minimal analytic requirements that we seek to satisfy. At the modeling stage, we also develop model-order reduction techniques, such as the use of reduced basis techniques or proper generalized decompositions, to tackle evolutive problems, in particular in the nonlinear case, and we are also interested in developing reduced-order methods for variational inequalities such as those encountered in solid mechanics with contact and possibly also friction.
3.2 Discretization by hybrid high-order and discrete element methods
We consequently design numerical methods for the devised model. Traditionally, we have worked in the context of finite element, finite volume, mixed finite element, and discontinuous Galerkin methods. Novel classes of schemes enable the use of general polygonal and polyhedral meshes with nonmatching interfaces, and we develop them in response to a high demand from our industrial partners (namely EDF, CEA, and IFP Energies Nouvelles). In the lowest-order case, our focus is to design discrete element methods for solid mechanics. The novelty is to devise these methods to treat dynamic elastoplasticity as well as quasi-static and dynamic crack propagation. We also develop structure-preserving methods for the Navier–Stokes equations, i.e., methods that mimic algebraically at the discrete level fundamental properties of the underlying PDEs, such as conservation principles and preservation of invariants. In the higher-order case, we actively contribute to the development of hybrid high-order methods. We contribute to the numerical analysis in nonlinear cases (obstacle problem, Signorini conditions), we apply these methods to challenging problems from solid mechanics involving large deformations and plasticity, and we develop a comprehensive software implementing them. We believe that these methods belong to the future generation of numerical methods for industrial simulations; as a concrete example, the implementation of these methods in an industrial software of EDF has been completed in 2019 in the framework of the PhD thesis of Nicolas Pignet.
3.3 Domain decomposition and Newton–Krylov (multigrid) solvers
We next concentrate an intensive effort on the development and analysis of efficient solvers for the systems of nonlinear algebraic equations that result from the above discretizations. We have in the past developed Newton–Krylov solvers like the adaptive inexact Newton method, and we place a particular emphasis on parallelization achieved via the domain decomposition method. Here we traditionally specialize in Robin transmission conditions, where an optimized choice of the parameter has already shown speed-ups in orders of magnitude in terms of the number of domain decomposition iterations in model cases. We concentrate in the SERENA project on adaptation of these algorithms to the above novel discretization schemes, on the optimization of the free Robin parameter for challenging situations, and also on the use of the Ventcell transmission conditions. Another feature is the use of such algorithms in time-dependent problems in space-time domain decomposition that we have recently pioneered. This allows the use of different time steps in different parts of the computational domain and turns out to be particularly useful in porous media applications, where the amount of diffusion (permeability) varies abruptly, so that the evolution speed varies significantly from one part of the computational domain to another. Our new theme here are Newton–multigrid solvers, where the geometric multigrid solver is tailored to the specific problem under consideration and to the specific numerical method, with problem- and discretization-dependent restriction, prolongation, and smoothing. Using patchwise smoothing, we have in particular recently developed a first multigrid method whose behavior is both in theory and in practice insensitive of (robust with respect to) the approximation polynomial degree. With patchwise techniques, we also achieve mass balance at each iteration step, a highly demanded feature in most of the target applications. The solver itself is then adaptively steered at each execution step by an a posteriori error estimate (adaptive stepsize, adaptive smoothing).
3.4 Reliability by a posteriori error control
The fourth part of our theoretical efforts goes towards guaranteeing the results obtained at the end of the numerical simulation. Here a key ingredient is the development of rigorous a posteriori estimates that make it possible to estimate in a fully computable way the error between the unknown exact solution and its numerical approximation. Our estimates also allow to distinguish the different components of the overall error, namely the errors coming from modeling, from the discretization scheme, from the nonlinear (Newton) solver, and from the linear algebraic (Krylov, domain decomposition, multigrid) solver. A new concept here is that of local stopping criteria, where all the error components are balanced locally within each computational mesh element. This naturally connects all parts of the numerical simulation process and gives rise to novel fully adaptive algorithms. We also theoretically address the question of convergence of the new fully adaptive algorithms. We identify theoretical conditions so that the error diminishes at each adaptive loop iteration by a contraction factor and we in particular derive a guaranteed error reduction factor in model cases. We have also proved a numerical optimality of the derived algorithms in model cases in the sense that, up to a generic constant, the smallest possible computational effort to achieve the given accuracy is needed.
3.5 Safe and correct programming
Finally, we concentrate on the issue of computer implementation of scientific computing programs. Increasing complexity of algorithms for modern scientific computing makes it a major challenge to implement them in the traditional imperative languages popular in the community. As an alternative, the computer science community provides theoretically sound tools for safe and correct programming. We explore here the use of these tools to design generic solutions for the implementation of the class of scientific computing software that we deal with. Our focus ranges from high-level programming via functional programming with OCaml through safe and easy parallelism via skeleton parallel programming with Sklml to proofs of correctness of numerical algorithms and programs via mechanical proofs with Coq.
4 Application domains
4.1 Multiphase flows and transport of contaminants in the subsurface
- subsurface depollution after chemical leakage
- nuclear waste disposal in deep underground repositories
- flow in large scale discrete fracture networks
- production of oil and gas
4.2 Industrial risks in energy production
- Stokes and Navier–Stokes flows related to nuclear reactor operation
- seismic wave propagation for detection and protection
- electromagnetism for interfaces between dielectrics and negative metamaterials
4.3 Nonlinear mechanics
- quasi-static and dynamic elastoplastic evolutions with small and large deformations
- quasi-static and dynamic crack propagation
- nonlinear contact and friction conditions
- application to engineering components mainly related to nuclear reactor operation and safety analysis
4.4 Computational quantum chemistry
- guaranteed bounds for ground-state energy (eigenvalues) and ground-state density matrix (eigenvectors) in first-principle molecular simulation
- application to Laplace, Gross–Pitaevskii, Kohn–Sham, and Schrödinger models
5 Social and environmental responsibility
5.1 Impact of research results
Via applications with our industrial and environmental partners EDF, CEA, IFP Energies Nouvelles, ANDRA, and BRGM.
6 Highlights of the year
Alexandre Ern brought to completion his eight-year long project with Jean-Luc Guermond on a comprehensive book in 3 volumes on Finite Elements (83 chapters, 500 exercises, 1300 pages).
Alexandre Ern published a book, co-authored with M. Cicuttin and N. Pignet, in the collection SpringerBriefs in Mathematics on Hybrid High-Order Methods.
Many new results of the ERC GATIPOR project in the ERC GATIPOR Gallery.
7 New software and platforms
7.1 New software
7.1.1 DiSk++
-
Name:
Discontinuous Skeletal C++ Library
-
Keywords:
High order methods, Polyhedral meshes, C++
-
Scientific Description:
Discontinuous Skeletal methods approximate the solution of boundary-value problems by attaching discrete unknowns to mesh faces (hence the term skeletal) while allowing these discrete unknowns to be chosen independently on each mesh face (hence the term discontinuous). Cell-based unknowns, which can be eliminated locally by a Schur complement technique (also known as static condensation), are also used in the formulation. Salient examples of high-order Discontinuous Skeletal methods are Hybridizable Discontinuous Galerkin methods and the recently-devised Hybrid High-Order methods. Some major benefits of Discontinuous Skeletal methods are that their construction is dimension-independent and that they offer the possibility to use general meshes with polytopal cells and non-matching interfaces. The mathematical flexibility of Discontinuous Skeletal methods can be efficiently replicated in a numerical software: by using generic programming, the DiSk++ library offers an environment to allow a programmer to code mathematical problems in a way completely decoupled from the mesh dimension and the cell shape.
-
Functional Description:
The software provides a numerical core to discretize partial differential equations arising from the engineering sciences (mechanical, thermal, diffusion). The discretization is based on the "Hybrid high-order" or "Discontinuous Skeletal" methods, which use as principal unknowns polynomials of arbitrary degree on each face of the mesh. An important feature of these methods is that they make it possible to treat general meshes composed of polyhedral cells. The DiSk ++ library, using generic programming techniques, makes it possible to write a code for a mathematical problem independently of the mesh. When a user writes the code for his problem using the basic operations offered by DiSk ++, that code can be executed without modifications on all types of mesh already supported by the library and those that will be added in the future.
- URL:
- Publication:
-
Author:
Matteo Cicuttin
-
Contact:
Matteo Cicuttin
-
Partner:
CERMICS
7.1.2 NEF++
-
Name:
NEF++
-
Keywords:
Fracture network, Finite element modelling, High order methods
-
Scientific Description:
NEF++ is able to solve in a very efficient way flow in large scale fractures networks using the HHO method.
-
Functional Description:
The software NEF++ allows to solve flow problems in fractured rocks. The discrete fracture network (DFN) framework is used to model the fractured rocks. As the mesh steps can be different from one fracture to another, the NEF++ software is able to manage matching and non matching meshes at the intersections between fractures. NEF++ is based on a hybrid high order (HHO) method. It is based on the C++17 standard. It relies on the Eigen library, which is a C++ template library for linear algebra and on the DiSk++ library for HHO. The linear systems can be solved with direct solvers or with iterative solvers like the preconditioned conjugate gradient or multigrid solvers.
-
Release Contributions:
NEF++ is now available as a Python module.
-
News of the Year:
Rotated basis functions are now implemented in NEF++ to ensure local mass conservation at high order.
- URL:
- Publications:
-
Contact:
Geraldine Pichot
-
Participants:
Florent Hedin, Geraldine Pichot, Alexandre Ern, Nicolas Pignet
7.1.3 ParaCirce
-
Name:
Parallel Circulant Embedding
-
Keywords:
2D, 3D, Hydrogeology, Gaussian random fields, MPI
-
Scientific Description:
ParaCirce implements the algorithm proposed by [C. R. Dietrich and G. N. Newsam. A fast and exact method for multidimensional gaussian stochastic simulations. Water Resources Research, 29(8):2861-2869, 1993] as well as an algorithm to accelerate the padding estimation
-
Functional Description:
ParaCirce implements a parallel Circulant Embedding method for the generation in parallel of 2D or 3D Gaussian Random Fields (second order stationary).
-
Release Contributions:
- Padding estimation - Use case examples - User documentation
-
News of the Year:
The main improvement of 2021 is the implementation of the acceleration of the padding estimation. User documentation has been made available online.
- URL:
- Publication:
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Simon Legrand
7.1.4 NEF-Flow-polygons
-
Name:
NEF-Flow-polygons
-
Keywords:
Fracture network, Large scale, High order finite elements
-
Scientific Description:
The motivation of this development comes from our interest in solving flow in Discrete Fracture Networks (DFN) with the Hybrid High Order (HHO) method. One option to reduce the computational cost in solving flow in large scale DFN is to mesh the fractures independently from one fracture to another, with a mesh step chosen in a efficient way (ideally from a posteriori estimators). Therefore the meshes are possibly non matching at the intersections. As the HHO method handles naturally elements of arbitrary shape, a vertices insertion strategy in a non matching mesh made of triangles allows to build a new matching mesh made of triangles and polygons. This new mesh is then suitable to be used in flow simulations solved with the HHO method.
-
Functional Description:
NEF-flow-polygons is a Matlab software to create a matching mesh made of triangles and polygons from a non matching triangular mesh of large scale discrete fracture networks (DFN). NEF-flow-polygons is interfaced with NEF++ to solve flow in these large DFN with the HHO method.
-
Release Contributions:
Implementation of the algorithm for creating geometrically conforming meshes. Set up of Conitnuous Integration (CI) on gitlab-inria.fr.
-
News of the Year:
Code optimization. NEF-flow-polygons has been successfully applied to various DFN, among with one with 1,176,566 fractures fractures meshed with 20,522,575 triangles.
- URL:
- Publications:
-
Contact:
Geraldine Pichot
-
Participant:
Geraldine Pichot
7.1.5 PyNKRT
-
Name:
A Python Newton-Krylov solver for Reactive Transport
-
Keywords:
Reactive transport, Nonlinear system, Python
-
Functional Description:
Python library for the simulation of reactive transport in porous media.
The library couples a transport module with a geochemistry module. The transport module is provided by the ComPASS code (developed by BRGM and Inria) and the chemistry module is developed as part of this project.
- URL:
-
Contact:
Michel Kern
-
Partner:
FSTG Marrakech
7.1.6 nef-flow-fpm
-
Keywords:
2D, 3D, Porous media, Fracture network, Geophysical flows
-
Scientific Description:
The code is based on the implementation of the mixed hybrid finite element method as detailed in: An efficient numerical model for incompressible two-phase flow in fractured media Hussein Hoteit, Abbas Firoozabadi, Advances in Water Resources 31, 891–905, 2008. https://doi.org/10.1016/j.advwatres.2008.02.004
The model of fractures and the coupling between the porous flow and the flow in the network of fractures is described in: : Modeling Fractures and Barriers as Interfaces for Flow in Porous Media V. Martin, J. Jaffré, J. E. Roberts, SIAM Journal on Scientific Computing, 2005. https://doi.org/10.1137/S1064827503429363
-
Functional Description:
nef-flow-fpm is a Matlab code to simulate flows in fractured porous media with the mixed-hybrid finite element methods (RT0).
-
Release Contributions:
Implementation of the mixed hybrid method for 3D porous flows, Discrete fracture Networks (DFN) flows and the coupling between DFN and porous flows.
-
News of the Year:
Add a validation benchmark test from the publication: Inga Berre, et al., Verification benchmarks for single-phase flow in three-dimensional fractured porous media, Advances in Water Resources, Volume 147, 2021. https://doi.org/10.1016/j.advwatres.2020.103759.
Add possible call to the linear solver AMGCL: https://amgcl.readthedocs.io/en/latest/
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Daniel Zegarra Vasquez, Michel Kern
7.1.7 Skwer
-
Keywords:
Differential equations, State-oriented solver
-
Functional Description:
Skwer aims at solving differential equations inherent to 0D physical modelling. This includes in particular standard ODEs but also differential equations with conditionals and "idealised behaviour" resulting from passing to the limit over some parameters.
-
Contact:
Sébastien Furic
-
Participants:
Sébastien Furic, Francois Clement, Geraldine Pichot
7.1.8 Coq-num-analysis
-
Keywords:
Coq, Numerical analyse, Real analysis
-
Scientific Description:
These Coq developments are based on the Coquelicot library for real analysis, they include the formalization and proof of: (1) the Lax-Milgram theorem, including results from linear algebra, geometry, functional analysis and Hilbert spaces, (2) the Lebesgue integral, including large parts of the measure theory,the building of the Lebesgue measure on real numbers, integration of nonnegative measurable functions with the Beppo Levi (monotone convergence) theorem, Fatou's lemma, the Tonelli theorem, and the Bochner integral with the dominated convergence theorem.
-
Functional Description:
Formal developments and proofs in Coq of numerical analysis problems. The long-term goal is to formally prove parts of a C++ library implementing the Finite Element Method.
-
News of the Year:
Formalization of the Bochner integral. Formalization of the Tonelli theorem. Migration to a public GIT repository.
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Sylvie Boldo, Francois Clement, Micaela Mayero, Vincent Martin, Stéphane Aubry, Florian Faissole, Houda Mouhcine, Louise Leclerc
-
Partners:
LIPN (Laboratoire d'Informatique de l'Université Paris Nord), LMAC (Laboratoire de Mathématiques Appliquées de Compiègne)
7.2 New platforms
8 New results
8.1 Hybrid high-order method for singularly perturbed fourth-order problems on curved domains.
Participants: Zhaonan Dong, Alexandre Ern.
In 27, we propose a novel hybrid high-order method (HHO) to approximate singularly perturbed fourth-order PDEs on domains with a possibly curved boundary. The two key ideas in devising the method are the use of a Nitsche-type boundary penalty technique to weakly enforce the boundary conditions and a scaling of the weighting parameter in the stabilization operator that compares the singular perturbation parameter to the square of the local mesh size. With these ideas in hand, we derive stability and optimal error estimates over the whole range of values for the singular perturbation parameter, including the zero value for which a second-order elliptic problem is recovered. Numerical experiments illustrate the theoretical analysis, cf. Figure 1.
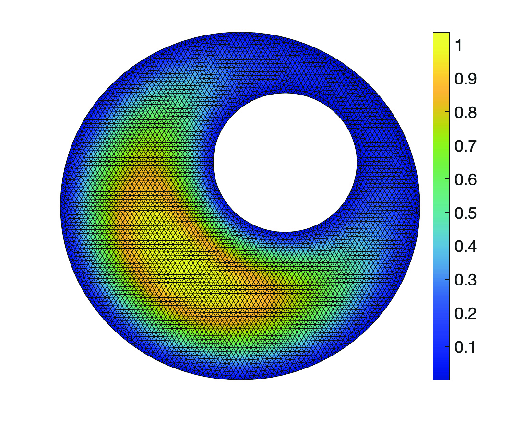
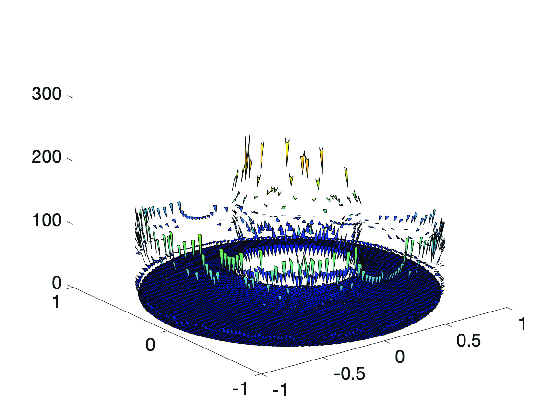
|
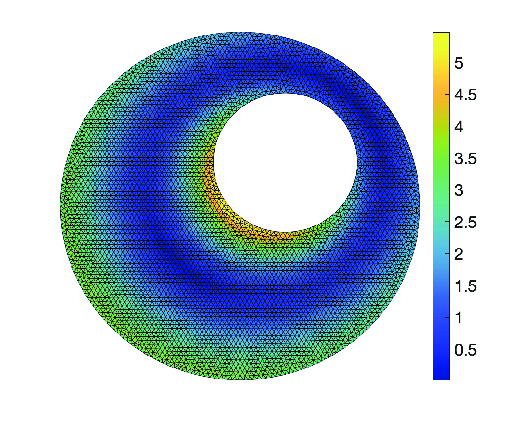
8.2 Stable broken polynomial extensions and -robust a posteriori error estimates in
Participants: Théophile Chaumont-Frelet, Alexandre Ern, Martin Vohralík.
In 25, we extend the results that we have previously established in the and context in 10 and 9 to the context. First, based on the seminal contributions in 72 and 73, we establish a stable broken polynomial extension on a patch of tetrahedra. We then use this result to design a posteriori error estimates of -conforming methods that possess the following crucial advantages: they are reliable (guaranteed), locally efficient, polynomial-degree-robust, and inexpensive. This in particular allows to certify the error committed in a numerical approximation of the simplified Maxwell problem, as well as to predict its spatial distribution, as illustrated in Figure 2.
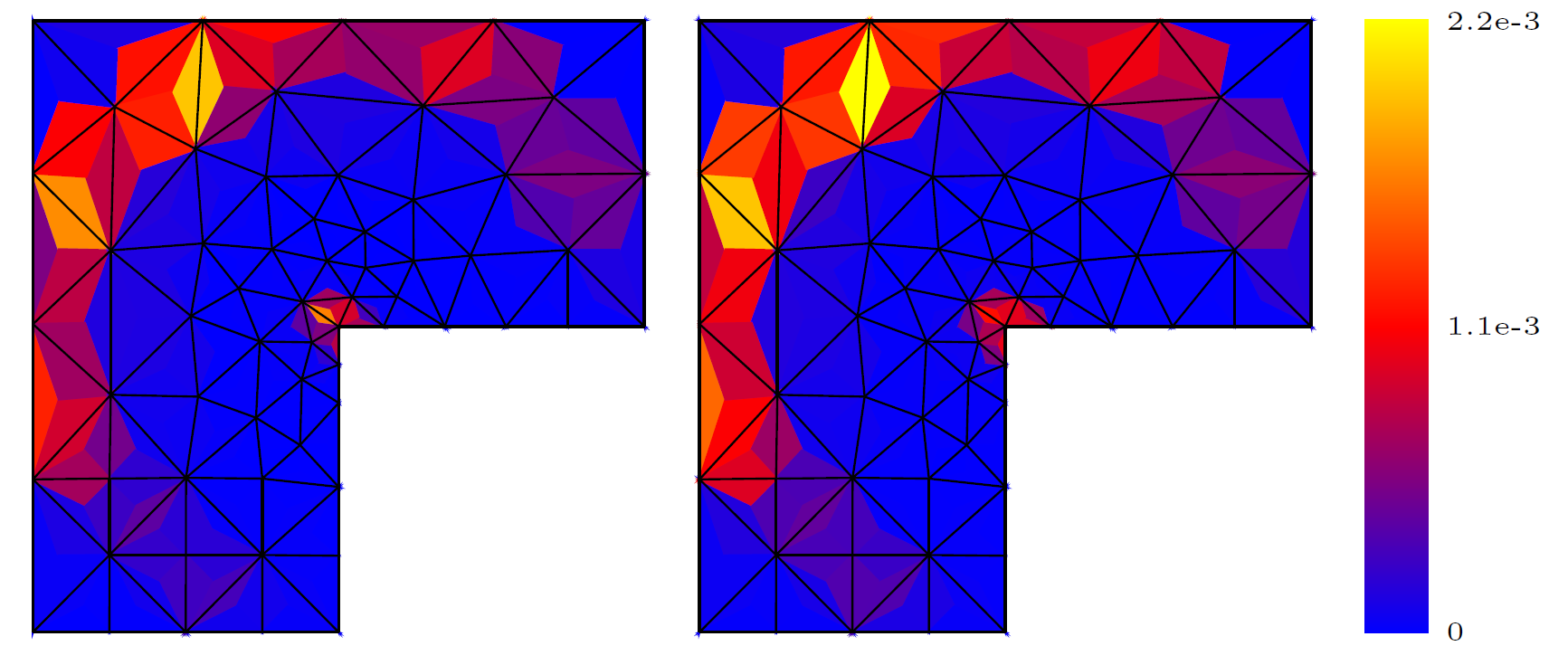
8.3 Hybrid high-order methods for flow simulations in extremely large discrete fracture networks
Participants: Alexandre Ern, Florent Hédin, Géraldine Pichot, Nicolas Pignet.
In 64, we investigate the computational performance of hybrid high-order methods applied to flow simulations in extremely large discrete fracture networks (over one million of fractures). We study the choice of basis functions, the trade-off between increasing the polynomial order and refining the mesh, and how to take advantage of polygonal cells to reduce the number of degrees of freedom. An example of gain obtained with a polygonal discretization over a traditional triangular discretization is presented in Figure 3.
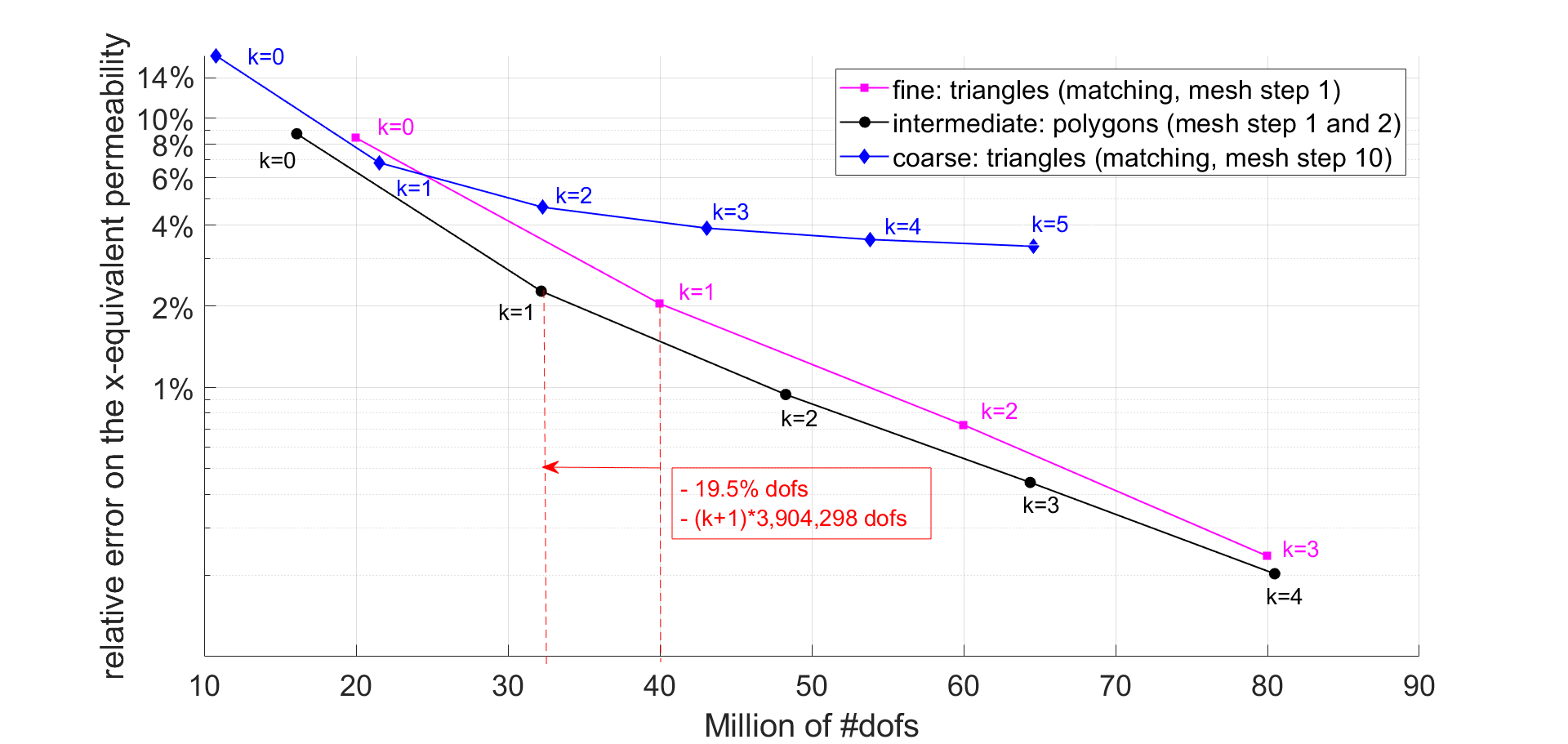
Relative error on the xx-equivalent permeability versus the number of dofs. Example of gain obtained with a polygonal discretization.
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
- Two-part contract with EDF accompanying the PhD thesis of Idrissa Niakh.
- Two-part contract with IFP Energies Nouvelles accompanying the PhD thesis of Joëlle Ferzly.
- Two-part contract with ANDRA accompanying the PhD thesis of Ari Rappaport.
- Two-part contract with CEA accompanying the PhD thesis of Morgane Steins.
- Two-part contract with CEA accompanying the PhD thesis of Romain Mottier.
10 Partnerships and cooperations
Informal international partners
University College London, Great Britain; Texas A&M University, USA; UPC (Spain); Institute of Mathematics, Czech Academy of Sciences; Charles University, Prague; Ecole Nationale d'Ingénieurs de Tunis
10.1 International research visitors
10.1.1 Visits of international scientists
Inria International Chair
Jean-Luc GUERMOND
-
Name of the chair:
Inria International Chair 2019–2023
-
Institution of origin:
Texas A&M University
-
Country:
United States
-
Dates:
From Jan 01 2019 to Dec 31 2023
-
Title:
Curved H(div), H(curl) elements, and magnetohydrodynamics & Approximation of hyperbolic systems
-
Summary:
The program is articulated around two themes: (1) Theoretical aspects in finite elements and applications to multi-physics magneto-hydrodynamics; (2) Finite element approximation of hyperbolic systems and applications. The results from this research will have applications in problems related to porous media flows, magnetohydrodynamics, water management, and compressible and incompressible fluid flows.
Other international visits to the team
See Section 1 Team members, visitors, external collaborators.
10.2 European initiatives
10.2.1 FP7 & H2020 projects
EMC2
-
Title:
Extreme-scale Mathematically-based Computational Chemistry
-
Duration:
2019 - 2025
-
Coordinator:
E. Cancès, L. Grigori, Y. Maday, J.-P. Piquemal
-
Partners:
- CENTRE NATIONAL DE LA RECHERCHE SCIENTIFIQUE
- ECOLE NATIONALE DES PONTS ET CHAUSSEES
- Inria
- Sorbonne Université
-
Inria contact:
L. Grigori
-
Summary:
The goal of this ERC Synergy is to develop physical and chemical models in chemistry, condensed matter physics, molecular biology, materials science, and nanosciences, altogether with mathematically-certified and numerically-efficient algorithms, and to implement them in a scalable way on various computer architectures.
- Web page:
GATIPOR
-
Title:
Guaranteed fully adaptive algorithms with tailored inexact solvers for complex porous media flows
-
Duration:
2015 - 2021
-
Coordinator:
M. Vohralík
-
Partners:
- Inria
-
Inria contact:
M. Vohralík
-
Summary:
The subject of this ERC consolidator grant are new approaches to porous media multiphase flows: inexact Newton-multigrid solvers, local stopping criteria, adaptivity, and a posteriori error control. The goal is to guarantee the overall simulation error and to speed-up importantly the present-day simulations.
- Web page:
11 Dissemination
11.1 Promoting scientific activities
11.1.1 Scientific events: organisation
Zhaonan Dong, Alexandre Ern, and Martin Vohralík (also with Jan Papež from the Czech Academy of Sciences in Prague) co-organized this year's edition of the European Finite Element Fair. The event was held in a hybrid format and hosted at Inria Paris on September 10–11, 2021.
Michel Kern organized (with Brahim Amaziane, Université de Pau) the Workshop SITRAM21 (Advances in the SImulation of reactive flow and TRAnsport in porous Media), December 8–9, 2021, Inria Paris.
Michel Kern is a co-organizer of the minisymposium "Mathematical and numerical methods for multi-scale multi-physics, nonlinear coupled processes" at the Interpore 2022 conference.
Guillaume Enchéry and Martin Vohralík have organized a 1-day workshop Journée contrat cadre IFP Energies Nouvelles/Inria.
Member of the organizing committees
Alexandre Ern is a member of the organizing committee of the European Finite Element Fair.
11.1.2 Scientific events: selection
Member of the conference program committees
Géraldine Pichot was a member of the Scientific Committee of the SIAM Conference on Mathematical & Computational Issues in the Geosciences (GS21), June 21–24, 2021, Politecnico di Milano, Italy.
Reviewer
François Clément served as reviewer for ITP21, and for CPP22.
11.1.3 Journal
Member of the editorial boards
Alexandre Ern is a member of the editorial boards of SIAM Journal on Scientific Computing, ESAIM Mathematical Modelling and Numerical Analysis, IMA Journal of Numerical Analysis, Journal of Scientific Computing, and Computational Methods in Applied Mathematics.
Martin Vohralík is a member of the editorial boards of Acta Polytechnica and Applications of Mathematics.
Reviewer - reviewing activities
Zhaonan Dong was a reviewer for the SIAM Journal on Numerical Analysis and SIAM Journal on Scientific Computing.
Alexandre Ern and Martin Vohralík have reviewed a dozen papers for various major journals of the field.
Michel Kern was a reviewer for SIAM Journal on Scientific Computing, Transport in Porous Media, Computer Methods in Applieds Mechanics and Engineering, Applicable Analysis and Mathematics and Computers in Simulation.
Géraldine Pichot was a reviewer for the SIAM/ASA Journal on Uncertainty Quantification.
11.1.4 Invited talks
Alexandre Ern gave one of the Plenary Talks at ICOSAHOM 2021 (virtual congress, Vienna, July 2021) and the Initial Lecture of the Australia-wide online seminar series on computational and numerical maths (February 2021).
Géraldine Pichot gave a keynote speech (50 minutes presentation) at the 2020+2021 edition of the bi-annual congress of the Italian Society of Applied and Industrial Mathematics SIMAI conference in Parma (August 30 to September 3, 2021).
Martin Vohralík was an invited speaker at PDEs in Fluid Mechanics 2021, online/Beyrouth, Liban, June 2021, Recent Advances in the Numerical Approximation of Partial Differential Equations, online/Milano, Italy, June 2021, and Numerical Analysis Workshop in Bielefeld, September 2021, Bielefeld, Germany.
11.1.5 Leadership within the scientific community
Alexandre Ern joined the Administration Board of SMAI and its Executive Committee as Vice-President in charge of relations with the industry.
Michel Kern is President of the C3I ("Certificat de Compétences en Calcul Intensif") Committee and a meber of the Scientific Board of Orap.
Martin Vohralík is a member of the steering committee of Summer schools CEA–EDF–INRIA.
Martin Vohralík is a member of the scientific board of the IFP Energies Nouvelles– Inria joint strategic partnership laboratory.
11.1.6 Scientific expertise
Michel Kern is a reviewer for the Allocation of Computing Time located at the Juelich Supercomputing Centre in Germany.
11.1.7 Research administration
François Clément is a member of the Comité local d'hygiène, de sécurité et des conditions de travail of the Inria Research Center of Paris.
Michel Kern is chair of the Comission de Développement Technologique of the Inria Paris Center.
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Licence : Alexandre Ern, Numerical analysis, 77h, L3/M1, Ecole Polytechnique, France.
- Master : Alexandre Ern, Discontinuous Galerkin methods, 20h, M2, Sorbonne University, France.
- Master: Michel Kern, Models and numerical methods for subsurface flow, 30h, M2, Université Paris Saclay, France.
- Master: Michel Kern, Advanced numerical analysis, 30h, M1, Institut Galilée, Université Paris-Nord, France.
- Master: Martin Vohralík, Advanced finite elements, 21h, M1, Ecole nationale supérieure de techniques avancées, Paris, France.
11.2.2 Supervision
- L3 Internship: Louise Leclerc, from June to July 2021, Formalization and proof in Coq of the Bochner integral, Sylvie Boldo (Toccata), François Clément.
- M2 Internship: Houda Mouhcine, from April to September 2021, Formalization and proof in Coq of the Tonelli theorem, Sylvie Boldo (Toccata), François Clément, Micaela Mayero (LIPN).
- Internship: Zuodong Wang, from June 2021 until September 2021, Hybrid high-order method for elliptic PDEs on curved and complicated domain, Zhaonan Dong.
- Intership: Daniel Zegarra-Vasquez (Sup-Galilée), April to September 2021, Simulation of flow in porous media with fractures, Géraldine Pichot and Michel Kern.
- PhD in progress: Joëlle Ferzly, A posteriori error estimates and adaptivity for complementarity problems, started 15 October 2019, Martin Vohralík.
- PhD in progress: Romain Mottier, Nonconfing hybrid methods for modeling and numerical simulation of seismo-acoustic wave propagation, started 01 November 2021, Alexandre Ern and Laurent Guillot (CEA).
- PhD in progress: Houda Mouhcine, Formal proofs in applied mathematics: verification of a generator for quadrature formulas, started 01 October 2021, Sylvie Boldo (Toccata), François Clément, Micaela Mayero (LIPN).
- PhD in progress: Idrissa Niakh, Reduced models for variational inequalities in computational mechanics, started 01 November 2019, Alexandre Ern and Virginie Ehrlacher (ENPC).
- PhD in progress: Stefano Piccardo, High-fidelity simulation of droplets in complex shear flows, started 01 October 2019, Alexandre Ern and Antonio Huerta (UPC).
- PhD in progress: Ari Rappaport, Adaptivity of model, linear and nonlinear solvers, and local conservation by post-processing. Application to transport problems in underground repositories, started 01 January 2021, Martin Vohralík and François Févotte (TriScale innov).
- PhD in progress: Morgane Steins, Hybrid high order methods for explicit dynamics of structures with adaptive mesh refinement, started 01 October 2020, Alexandre Ern and Martin Vohralík.
- PhD in progress: Daniel Zegarra Vasquez, High-performance simulation of single-phase flows in a fractured porous medium, started 01 October 2021, Michel Kern, Géraldine Pichot, and Martin Vohralík.
11.2.3 Juries
Alexandre Ern was a reviewer for the HDR defense of Aline Lefebvre-Lepot (IPP, December 2021) and a reviewer for the PhD thesis of Michele Giuliano Carlino (University of Bordeaux, December 2021). He was also the chair of the committee for the HDR of Olga Mula (Dauphine University, December 2021).
Michel Kern was an axaminer for the HDR of Laila Amir (Université de Marrakech, Morocco, April 2021), and for the PhD of Pierre Jacquet (Université de Pau, February 2021).
Géraldine Pichot was an examiner for the PhD thesis of Miao Yu (University of Paris, December 2021). She was also a member of the jury of the DT1 position: Ingénieur expérimentation et développement (h/f), Inria, September–October 2021. She also served as a member of the evaluation committee: permanent researcher position in computational geoscience, University of Bergen, February 2021.
Martin Vohralík served as referee and committee member for the PhD thesis defense of Manuela Bastidas Olivares (Hasselt University, Belgium, March 2021). He also served as referee and committee member for the PhD thesis defense of Stefan Schimanko (Vienna University of Technology, Austria, June 2021). He further served as a committee member for the PhD thesis defense of Manu Jayadharan (University of Pittsburgh, USA, July 2021). He also served as referee and committee member for the PhD thesis defense of André Harnist (Université de Montpellier, October 2021). He further served as the chair of the committee for the PhD thesis of Daria Koliesnikova (Aix Marseille Université, July 2021). He finally served as referee and committee member for the HDR sefense of Stella Krell (Université Côte d’Azur, June 2021).
11.3 Popularization
11.3.1 Internal or external Inria responsibilities
Géraldine Pichot is a member of the editorial committee of Interstices.
11.3.2 Interventions
Géraldine Pichot, Conference at the RJMI (Rendez-vous des Jeunes Mathématiciennes et Informaticiennes), November 3, 2021.
12 Scientific production
12.1 Major publications
- 1 articleA posteriori error estimates and stopping criteria for space-time domain decomposition for two-phase flow between different rock types.SMAI Journal of Computational Mathematics5December 2019, 195-227
- 2 articleTrusting computations: A mechanized proof from partial differential equations to actual program.Computers and Mathematics with Applications683August 2014, 325--352
- 3 articleWave equation numerical resolution: a comprehensive mechanized proof of a C program.Journal of Automated Reasoning504April 2013, 423--456
- 4 articleGuaranteed and robust a posteriori bounds for Laplace eigenvalues and eigenvectors: conforming approximations.SIAM Journal on Numerical Analysis555September 2017, 2228-2254
-
5
article
-Version discontinuous Galerkin methods on essentially arbitrarily-shaped elements.Mathematics of Computation91333January 2022, 1-35 - 6 articleA hybrid high-order locking-free method for linear elasticity on general meshes.Comput. Methods Appl. Mech. Engrg.2832015, 1--21URL: http://dx.doi.org/10.1016/j.cma.2014.09.009
-
7
articleEquivalence of local-and global-best approximations, a simple stable local commuting projector, and optimal
approximation estimates in (div).IMA Journal of Numerical AnalysisMarch 2021 - 8 articleFinite element quasi-interpolation and best approximation.ESAIM Math. Model. Numer. Anal.5142017, 1367--1385URL: https://doi.org/10.1051/m2an/2016066
- 9 articlePolynomial-degree-robust a posteriori estimates in a unified setting for conforming, nonconforming, discontinuous Galerkin, and mixed discretizations.SIAM Journal on Numerical Analysis532April 2015, 1058-1081
- 10 articleStable broken H1 and H(div) polynomial extensions for polynomial-degree-robust potential and flux reconstruction in three space dimensions.Mathematics of Computation89322March 2020, 551-594
- 11 articleSpace-time domain decomposition methods for diffusion problems in mixed formulations.SIAM J. Numer. Anal.5162013, 3532--3559URL: http://dx.doi.org/10.1137/130914401
- 12 articleSimulating diffusion processes in discontinuous media: a numerical scheme with constant time steps.J. Comput. Phys.231212012, 7299--7314URL: http://dx.doi.org/10.1016/j.jcp.2012.07.011
- 13 articleA generalized mixed hybrid mortar method for solving flow in stochastic discrete fracture networks.SIAM J. Sci. Comput.3412012, B86--B105URL: http://dx.doi.org/10.1137/100804383
12.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Scientific books
Reports & preprints
12.3 Cited publications
- 72 articleOn Bogovskiĭ and regularized Poincaré integral operators for de Rham complexes on Lipschitz domains.Math. Z.26522010, 297--320URL: http://dx.doi.org/10.1007/s00209-009-0517-8
- 73 articlePolynomial extension operators. Part II.SIAM J. Numer. Anal.4752009, 3293--3324URL: http://dx.doi.org/10.1137/070698798

