VERIDIS - 2021 - Annual activity report

VERIDIS

VERIDIS - 2021

2021

Activity report

Project-Team

VERIDIS

RNSR: 201020692C

Research center

Nancy - Grand Est

In partnership with:

CNRS, Université de Lorraine, Max-Planck-Institut für Informatik Saarbrücken

Modeling and Verification of Distributed Algorithms and Systems

In collaboration with:

Laboratoire lorrain de recherche en informatique et ses applications (LORIA)

Domain

Algorithmics, Programming, Software and Architecture

Theme

Proofs and Verification

Creation of the Project-Team: 2012 July 01

Keywords

Computer Science and Digital Science

A2.1.7. Distributed programming
A2.1.11. Proof languages
A2.4. Formal method for verification, reliability, certification
A2.4.1. Analysis
A2.4.2. Model-checking
A2.4.3. Proofs
A2.5. Software engineering
A7.2. Logic in Computer Science
A8.4. Computer Algebra

1 Team members, visitors, external collaborators

Research Scientists

Stephan Merz [Team leader, Inria, Senior Researcher, HDR]
Engel Escaffre-Lefaucheux [Inria, from October 2021, Starting Faculty Position]
Ioannis Filippidis [Inria, Starting Research Position]
Thomas Sturm [CNRS, Senior Researcher, HDR]
Sophie Tourret [Inria, Researcher]
Uwe Waldmann [Max Planck Society, Researcher]
Christoph Weidenbach [Max Planck Society, Senior Researcher, HDR]

Faculty Members

Étienne André [Univ de Lorraine, Professor, HDR]
Horatiu Cirstea [Univ de Lorraine, Professor, HDR]
Marie Duflot-Kremer [Univ de Lorraine, Associate Professor]
Serguei Lenglet [Univ de Lorraine, Associate Professor]
Pierre-Etienne Moreau [Univ de Lorraine, Professor, HDR]
Dominique Méry [Univ de Lorraine, Professor]
Sorin Stratulat [Univ de Lorraine, Associate Professor, HDR]

Post-Doctoral Fellows

Johan Arcile [Univ de Lorraine]
Martin Bromberger [Max Planck Society]
Zheng Cheng [Univ de Lorraine]
Hamid Rahkooy [Max Planck Society]

PhD Students

Antoine Defourné [Inria]
Martin Desharnais [Max Planck Society]
Daniel El Ouraoui [Inria, until February 2021]
Fajar Haifani [Max Planck Society]
Hendrik Leidinger [Max Planck Society]
Pierre Lermusiaux [Univ de Lorraine, ATER]
Lorenz Leutgeb [Max Planck Society]
Dylan Marinho [Université de Lorraine]
Hans Jörg Schurr [Univ de Lorraine, Inria until August 2021, ATER since September 2021]

Technical Staff

George Krait [Inria, Engineer, from February 2021]
Benjamin Loillier [Inria, Engineer]

Interns and Apprentices

Sonal Ramchandra Dhage [Inria, from March 2021 until July 2021]
Alexis Larcher [Univ de Lorraine, from April 2021 until June 2021]
Dostonbek Matyakubov [Inria, from March 2021 until July 2021]
Qi Qiu [Inria, from April 2021 until July 2021]
Vincent Trélat [Univ de Lorraine, from September 2021]

Administrative Assistants

Sophie Drouot [Inria]
Sylvie Hilbert [CNRS]

External Collaborators

Jasmin Christian Blanchette [Free University of Amsterdam, The Netherlands]
Pascal Fontaine [University of Liège, Belgium, HDR]

2 Overall objectives

The VeriDis project team includes members of the MOSEL group at LORIA, the computer science laboratory in Nancy, and members of the research group Automation of Logic at Max-Planck-Institut für Informatik in Saarbrücken. It is headed by Stephan Merz and Christoph Weidenbach. VeriDis was created in 2010 as a local research group of Inria Nancy – Grand Est and has been an Inria project team since July 2012.

The objectives of VeriDis are to contribute to advances in verification techniques, including automated and interactive theorem proving, and to make them available for the development and analysis of concurrent and distributed algorithms and systems, based on mathematically precise and practically applicable development methods. The techniques that we develop are intended to assist designers of algorithms and systems in carrying out formally verified developments, where proofs of relevant properties, as well as bugs, can be found with a high degree of automation.

Within this context, we work on techniques for automated theorem proving for expressive languages based on first-order logic, with support for theories (fragments of arithmetic, set theory etc.) that are relevant for specifying algorithms and systems. Ideally, systems and their properties would be specified using high-level, expressive languages, errors in specifications would be discovered automatically, and finally, full verification could also be performed completely automatically. Due to the fundamental undecidability of the problem, this cannot be achieved in general. Nevertheless, we have observed important advances in automated deduction in recent years, to which we have contributed. These advances suggest that a substantially higher degree of automation can be achieved over what is available in today's tools supporting deductive verification. Our techniques are developed within SMT (satisfiability modulo theories) solving and superposition reasoning, the two main frameworks of contemporary automated reasoning that have complementary strengths and weaknesses, and we are interested in making them converge when appropriate. Techniques developed within the symbolic computation domain, such as algorithms for quantifier elimination for appropriate theories, are also relevant, and we are working on integrating them into our portfolio of techniques. In order to handle expressive input languages, we are working on techniques that encompass tractable fragments of higher-order logic, for example for specifying inductive or co-inductive data types, for automating proofs by induction, or for handling collections defined through a characteristic predicate.

Since full automatic verification remains elusive, another line of our research targets interactive proof platforms. We intend these platforms to benefit from our work on automated deduction by incorporating powerful automated backends and thus raise the degree of automation beyond what current proof assistants can offer. Since most conjectures stated by users are initially wrong (due to type errors, omitted hypotheses or overlooked border cases), it is also important that proof assistants be able to detect and explain such errors rather than letting users waste considerable time in futile proof attempts. Moreover, increased automation must not come at the expense of trustworthiness: skeptical proof assistants expect to be given an explanation of the proof found by the backend prover that they can certify.

Model checking is also an established and highly successful technique for verifying systems and for finding errors. Our contributions in this area more specifically target quantitative, in particular timed or probabilistic systems. A specificity of VeriDis is notably to consider partially specified systems, using parameters, in which case the verification problem becomes the synthesis of suitable parameter valuations.

Our methodological and foundational research is accompanied by the development of efficient software tools, several of which go beyond pure research prototypes: they have been used by others, have been integrated in verification platforms developed by other groups, and participate in international competitions. We also validate our work on verification techniques by applying them to the formal development of algorithms and systems. We mainly target high-level descriptions of concurrent and distributed algorithms and systems. This class of algorithms is by now ubiquitous, ranging from multi- and many-core algorithms to large networks and cloud computing, and their formal verification is notoriously difficult. Targeting high levels of abstraction allows the designs of such systems to be verified before an actual implementation has been developed, contributing to reducing the costs of formal verification. The potential of distributed systems for increased resilience to component failures makes them attractive in many contexts, but also makes formal verification even more important and challenging. Our work in this area aims at identifying classes of algorithms and systems for which we can provide guidelines and identify patterns of formal development that makes verification less an art and more an engineering discipline. We mainly target components of operating systems, distributed and cloud services, and networks of computers or mobile devices.

Beyond formal system verification, we pursue applications of some of the symbolic techniques that we develop in other domains. We have observed encouraging success in using techniques of symbolic computation for the qualitative analysis of biological and chemical networks described by systems of ordinary differential equations that were previously only accessible to large-scale simulation. Such networks include biological reaction networks as they occur with models for diseases such as diabetes or cancer. They furthermore include epidemic models such as variants and generalizations of SEIR1 models, which are typically used for Influenza A or Covid-19. This work is being pursued within a large-scale interdisciplinary collaboration. It aims for our work grounded in verification to have an impact on the sciences, beyond engineering, which will feed back into our core formal methods community.

3 Research program

3.1 Automated and Interactive Theorem Proving

The VeriDis team gathers experts in techniques and tools for automatic deduction and interactive theorem proving, and specialists in methods and formalisms designed for the development of trustworthy concurrent and distributed systems and algorithms. Our common objective is twofold: first, we wish to advance the state of the art in automated and interactive theorem proving, and their combinations. Second, we work on making the resulting technology available for the computer-aided verification of distributed systems and protocols. In particular, our techniques and tools are intended to support sound methods for the development of trustworthy distributed systems that scale to algorithms relevant for practical applications.

VeriDis members from Saarbrücken are developing the Spass 10workbench. It currently consists of one of the leading automated theorem provers for first-order logic based on the superposition calculus 73 and a theory solver for linear arithmetic 2. Recently we have extended it to a Datalog hammer solving universal and existential queries with respect to a Horn Bernays-Schoenfinkel Horn theory modulo linear arithmetic 29, 28.

In a complementary approach to automated deduction, VeriDis members from Nancy work on techniques for integrating reasoners for specific theories. They develop veriT1, an SMT 2 solver that combines decision procedures for different fragments of first-order logic. The veriT solver is designed to produce detailed proofs; this makes it particularly suitable as a component of a robust cooperation of deduction tools.

Finally, VeriDis members design effective quantifier elimination methods and decision procedures for algebraic theories, supported by their efficient implementation in the Redlog system 5.

An important objective of this line of work is the integration of theories in automated deduction. Typical theories of interest, including fragments of arithmetic, are difficult or impossible to express in first-order logic. We therefore explore efficient, modular techniques for integrating semantic and syntactic reasoning methods, develop novel combination results and techniques for quantifier instantiation. These problems are addressed from both sides, i.e. by embedding decision procedures into the superposition framework or by allowing an SMT solver to accept axiomatizations for plug-in theories. We also develop specific decision procedures for theories such as non-linear real arithmetic that are important when reasoning about certain classes of (e.g., real-time) systems but that also have interesting applications beyond verification.

We rely on interactive theorem provers for reasoning about specifications at a high level of abstraction when fully automatic verification is not (yet) feasible. An interactive proof platform should help verification engineers lay out the proof structure at a sufficiently high level of abstraction; powerful automatic plug-ins should then discharge the resulting proof steps. Members of VeriDis have ample experience in the specification and subsequent machine-assisted, interactive verification of algorithms. In particular, we participate in a project at the joint Microsoft Research-Inria Centre on the development of methods and tools for the formal proof of specifications written in the TLA+85 language. Our prover relies on a declarative proof language, and calls upon several automatic backends 4. Trust in the correctness of the overall proof can be ensured when the backends provide justifications that can be checked by the trusted kernel of a proof assistant. During the development of a proof, most obligations that are passed to the prover actually fail – for example, because necessary information is not present in the context or because the invariant is too weak, and we are interested in explaining failed proof attempts to the user, in particular through the construction of counter-models.

Members of VeriDis formalize a framework in the proof assistant Isabelle/HOL for representing the correctness and completeness of automated theorem provers. This work encompasses proof calculi such as ordered resolution or superposition, as well as concrete prover architectures such as Otter or DISCOUNT loops. It also covers the most recent splitting techniques that bring proof calculi closer to SMT solvers.

3.2 Formal Methods for Developing and Analyzing Algorithms and Systems

Theorem provers are not used in isolation, but they support the application of sound methodologies for modeling and verifying systems. In this respect, members of VeriDis have gained expertise and recognition in making contributions to formal methods for concurrent and distributed algorithms and systems 3, 8, and in applying them to concrete use cases. In particular, the concept of refinement69, 74, 90 in state-based modeling formalisms is central to our approach because it allows us to present a rational (re)construction of system development. An important goal in designing such methods is to establish precise proof obligations, many of which can be discharged by automatic tools. This requires taking into account specific characteristics of certain classes of systems and tailoring the model to concrete computational models. Our research in this area is supported by carrying out case studies for academic and industrial developments. This activity benefits from and influences the development of our proof tools.

In this line of work, we investigate specific development and verification patterns for particular classes of algorithms, in order to reduce the work associated with their verification. We are also interested in applications of formal methods and their associated tools to the development of systems that underlie specific certification requirements in the sense of, e.g., Common Criteria. Finally, we are interested in the adaptation of model checking techniques for verifying actual distributed programs, rather than high-level models.

Today, the formal verification of a new algorithm is typically the subject of a PhD thesis, if it is addressed at all. This situation is not sustainable given the move towards more and more parallelism in mainstream systems: algorithm developers and system designers must be able to productively use verification tools for validating their algorithms and implementations. On a high level, the goal of VeriDis is to make formal verification standard practice for the development of distributed algorithms and systems, just as symbolic model checking has become commonplace in the development of embedded systems and as security analysis for cryptographic protocols is becoming standard practice today. Although the fundamental problems in distributed programming are well-known, they pose new challenges in the context of modern system paradigms, including ad-hoc and overlay networks or peer-to-peer systems, and they must be integrated for concrete applications.

Model checking

The paradigm of model checking is based on automatically verifying properties over a formal model of a system, using mathematical foundations. Model checking, while useful and highly successful in practice, can encounter the infamous state space explosion problem. One direction of VeriDis therefore addresses the efficiency of model checking, by proposing new algorithms or heuristics to speed up analysis. We notably focus on the quantitative setting (time, probabilities), and more specifically on the parametric paradigm where some quantitative constants are unknown, and the goal becomes to synthesize suitable valuations.

3.3 Verification and Analysis of Dynamic Properties of Biological Systems

The unprecedented accumulation of information in biology and medicine during the last 20 years led to a situation where any new progress in these fields is dependent on the capacity to model and make sense of large data. Until recently, foundational research was concerned with simple models of 2 to 5 ordinary differential equations. The analysis of even such simple models was sufficiently involved that it resulted in one or several scientific publications for a single model. Much larger models are built today to represent cell processes, explain and predict the origin and evolution of complex diseases or the differences between patients in precision and personalized medicine. For instance, the biomodels.net model repository 88 contains thousands of hand-built models of up to several hundreds of variables. Numerical analysis of large models requires an exhaustive scan of the parameter space or the identification of the numerical parameters from data. Both is infeasible for large biological systems because parameters are largely unknown and because of the curse of dimensionality: data, even rich, become rapidly sparse when the dimensionality of the problem increases. On these grounds, VeriDis researchers aim at formal symbolic analysis instead of numerical simulation. This complements VeriDis's engineering-oriented research with another research line in the natural sciences, noticing that at an adequate level of abstraction, problems and algorithmic approaches to their solutions resemble each other.

To get an impression, consider BIOMD0000000716 in the above-mentioned BioModels database, which models the transmission dynamics of subtype H5N6 of the avian Influenza A virus in the Philippines in August 2017 89. There are four species: S_b (susceptible bird), I_b (infected bird), S_h (susceptible human), and I_h (infected human). Denoting their concentrations over time we denote by differential variables $y_{1}, \dots, y_{4}$ , respectively, we obtain the following dynamics:

\begin{matrix} {\dot{y}}_{1} & = - \frac{9137}{2635182} y_{1} y_{2} - \frac{1}{730} y_{1} + \frac{412}{73}, & {\dot{y}}_{2} & = \frac{9137}{2635182} y_{1} y_{2} - \frac{4652377}{961841430} y_{2}, \\ {\dot{y}}_{3} & = - \frac{1}{6159375000} y_{2} y_{3} - \frac{1}{25258} y_{3} + \frac{40758549}{3650000}, & {\dot{y}}_{4} & = \frac{1}{6159375000} y_{2} y_{3} - \frac{112500173}{2841525000000} y_{4} . \end{matrix}

Using exclusively formal methods on this dynamics, we algorithmically obtain a decomposition of the dynamics into three sub-systems $T_{1}$ , ..., $T_{3}$ with respective attractive manifolds $ℳ_{1}$ , ..., $ℳ_{3}$ :

\begin{matrix} T_{1} & : {\dot{y}}_{1} = 1 \cdot (- \frac{9137}{2635182} y_{1} y_{2} + \frac{412}{73}), {\dot{y}}_{2} = {\dot{y}}_{3} = {\dot{y}}_{4} = 0 \\ ℳ_{1} & : y_{1} y_{2} = \frac{1085694984}{667001} \\ T_{2} & : {\dot{y}}_{2} = \frac{1}{125} \cdot (- \frac{116309425}{192368286} y_{2} + \frac{51500}{73}), {\dot{y}}_{3} = {\dot{y}}_{4} = 0 \\ ℳ_{2} & : y_{1} = \frac{4652377}{3335005}, y_{2} = \frac{5428474920}{4652377} \\ T_{3} & : {\dot{y}}_{3} = \frac{1}{15625} \cdot (- \frac{15625}{25258} y_{3} + \frac{203792745}{1168}), {\dot{y}}_{4} = \frac{1}{15625} \cdot (\frac{15079097}{5094352815} y_{3} - \frac{112500173}{181857600} y_{4}) \\ ℳ_{3} & : y_{1} = \frac{4652377}{3335005}, y_{2} = \frac{5428474920}{4652377}, y_{3} = \frac{7051228977}{25000}, y_{4} = \frac{441466240042010928888}{327120760850763125} . \end{matrix}

The explicit constant factors on the right hand sides of the differential equations $T_{i}$ make explicit that the system $T_{2}$ is 125 times slower than $T_{1}$ , and $T_{3}$ is another 125 times slower.

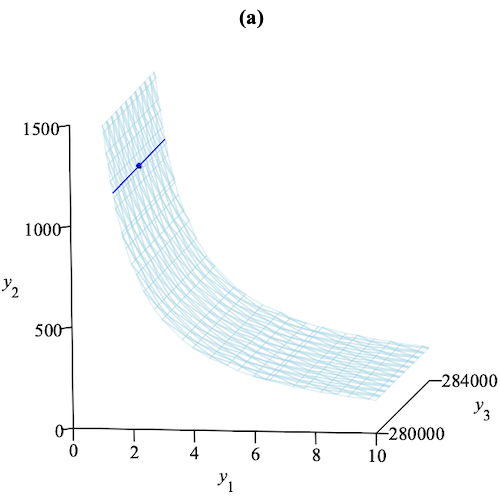
Figure 1.a — Figure 1: Reduction of an epidemic model of avian Influenza A. (a) The surface is the critical manifold $ℳ_{1}$ projected from $ℝ^{4}$ into real $(y_{1}, y_{2}, y_{3})$ -space. The line located at $(y_{1}, y_{2}) \approx (1.4, 1166.8)$ is the critical submanifold $ℳ_{2} \subseteq ℳ_{1}$ . The dot located at $(y_{1}, y_{2}, y_{3}) \approx (1.4, 1166.8, 282049.2)$ is the critical submanifold $ℳ_{3} \subseteq ℳ_{2}$ . Both $ℳ_{1}$ and $ℳ_{2}$ extend to $\pm \infty$ in both $y_{3}$ and $y_{4}$ direction, and $ℳ_{3}$ is located near $(1.4, 1166.8, 282049.2, 1349.6)$ . (b) The direction field of $T_{1}$ projected from $ℝ^{4}$ into real $(y_{1}, y_{2})$ -space. The curve is the critical manifold $ℳ_{1}$ . (c) The direction field of $T_{2}$ on $ℳ_{1}$ projected from $ℝ^{4}$ into real $(y_{3}, y_{2})$ -space. The line is the critical submanifold $ℳ_{2} \subseteq ℳ_{1}$ . (d) The direction field of $T_{3}$ on $ℳ_{2}$ projected from $ℝ^{4}$ into real $(y_{3}, y_{4})$ -space. The dot is the critical submanifold $ℳ_{3} \subseteq ℳ_{2}$ .

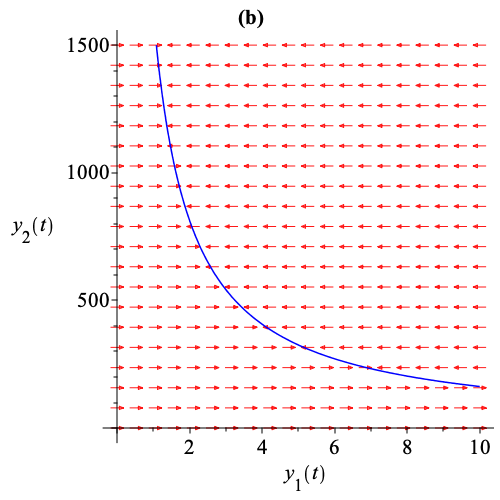
Figure 1.b — Figure 1: Reduction of an epidemic model of avian Influenza A. (a) The surface is the critical manifold $ℳ_{1}$ projected from $ℝ^{4}$ into real $(y_{1}, y_{2}, y_{3})$ -space. The line located at $(y_{1}, y_{2}) \approx (1.4, 1166.8)$ is the critical submanifold $ℳ_{2} \subseteq ℳ_{1}$ . The dot located at $(y_{1}, y_{2}, y_{3}) \approx (1.4, 1166.8, 282049.2)$ is the critical submanifold $ℳ_{3} \subseteq ℳ_{2}$ . Both $ℳ_{1}$ and $ℳ_{2}$ extend to $\pm \infty$ in both $y_{3}$ and $y_{4}$ direction, and $ℳ_{3}$ is located near $(1.4, 1166.8, 282049.2, 1349.6)$ . (b) The direction field of $T_{1}$ projected from $ℝ^{4}$ into real $(y_{1}, y_{2})$ -space. The curve is the critical manifold $ℳ_{1}$ . (c) The direction field of $T_{2}$ on $ℳ_{1}$ projected from $ℝ^{4}$ into real $(y_{3}, y_{2})$ -space. The line is the critical submanifold $ℳ_{2} \subseteq ℳ_{1}$ . (d) The direction field of $T_{3}$ on $ℳ_{2}$ projected from $ℝ^{4}$ into real $(y_{3}, y_{4})$ -space. The dot is the critical submanifold $ℳ_{3} \subseteq ℳ_{2}$ .

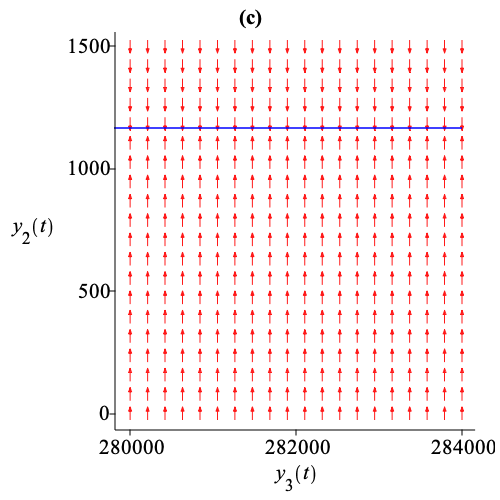
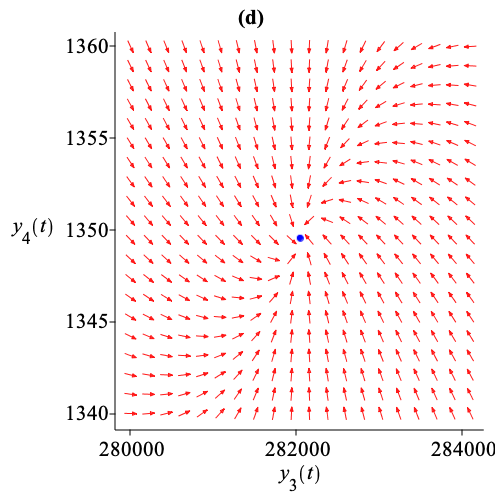
This multiple time scale reduction emphasizes a cascade of successive relaxations of model variables. First, the population of susceptible birds relaxes, meaning that these variables reach quasi-steady state values as shown in Fig. 1(b). Then the population of infected birds relaxes as shown in Fig. 1(c). Finally, the populations of susceptible and infected humans relax to a stable steady state as shown in Fig. 1(d), while following a reduced dynamics described by $T_{3}$ .

The computation time is less than a second. The computation is based on massive SMT solving over various theories, including QF_LRA for tropicalizations, QF_NRA for testing Hurwitz conditions on eigenvalues, and QF_LIA for finding sufficient differentiability conditions for hyperbolic attractivity of critical manifolds. Gröbner reduction techniques are used for final algebraic simplification 18. Observe that numerical simulation would not be able to provide such a global analysis of the overall system, even in the absence of symbolic parameters, as is the case in our rather simple example.

4 Application domains

Distributed algorithms and protocols are found at all levels of computing infrastructure, from many-core processors and systems on chip to wide-area networks. We are particularly interested in the verification of algorithms that are developed for supporting novel computing paradigms, including ad-hoc networks that underly mobile and low-power computing or overlay networks, peer-to-peer networks that provide services for telecommunication, or cloud computing services. Computing infrastructure must be highly available and is ideally invisible to the end user, therefore correctness is crucial. One should note that standard problems of distributed computing such as consensus, group membership or leader election have to be reformulated for the dynamic context of these modern systems. We are not ourselves experts in the design of distributed algorithms, but we work together with domain experts on designing formal models of these protocols, and on verifying their properties. These cooperations help us focus on concrete algorithms and ensure that our work is relevant to the distributed algorithm community.

Our work on symbolic procedures for solving polynomial constraints finds applications beyond verification. In particular, we have been working in interdisciplinary projects with researchers from mathematics, computer science, systems biology, and system medicine on the analysis of reaction networks and epidemic models in order to infer principal qualitative properties. Our techniques complement numerical analysis techniques and are validated against collections of models from computational biology.

Our work on parametric timed automata is partly motivated by applications in cybersecurity, notably within the ANR-NRF ProMiS project (cf. section 9.1.1). Foundational decidability results 71, 72 and novel notions of non-interference for this class of automata allow us, for example, to determine the maximal frequency of attacker actions for the attack to succeed (i.e., so that these actions remain invisible to the external observer). These methods can also be applied to the analysis of attack-fault trees 13 and formally derive parameter valuations (representing time or cost) for which an attack-fault tree is safe or, on the other hand, for which an attack is possible.

5 Highlights of the year

5.1 Awards

The developers of the theorem prover Zipperposition, including Alexander Bentkamp, Jasmin Blanchette, Simon Cruanes, Visa Nummelin, Sophie Tourret, and Petar Vukmirović, secured the first-place trophy at the 2021 edition of the CADE ATP System Competition (CASC) in the higher-order division for the second year in a row.

Jasmin Blanchette, Sascha Böhme, and Lawrence Paulson received the Skolem (test-of-time) award at CADE 2021 for their 2011 paper “Extending Sledgehammer with SMT Solvers” 76.

Hans-Jörg Schurr and Pascal Fontaine received the best student paper award at FroCos 2021 for their paper “Quantifier Simplification by Unification in SMT”35.

Louis Penet de Monterno, Bernadette Charron-Bost, and Stephan Merz received the best paper award at SSS 2021 for their paper “Synchronization Modulo $k$ in Dynamic Networks”42.

Petar Vukmirović, Jasmin Blanchette, Simon Cruanes, Visa Nummelin, and Sophie Tourret were honored with the best student paper award at CADE 2021 for their paper “Making Higher-Order Superposition Work”51.

6 New software and platforms

6.1 New software

6.1.1 IMITATOR

Name:
IMITATOR
Keywords:
Verification, Parametric model, Parameter synthesis, Model Checking, Model Checker, Timed automata
Functional Description:
IMITATOR is a software tool for parametric verification and robustness analysis of real-time systems with parameters. It relies on the formalism of networks of parametric timed automata, augmented with integer variables and stopwatches.
News of the Year:
New algorithm for NDFS-based cycle synthesis (by Laure Petrucci and Jaco Van de Pol). Extension of the syntax: if-then-else conditions allowed in updated, #include allowed for submodel inclusion. New applications to cybersecurity.
URL:
https://www.imitator.fr/
Publications:
hal-00785289, hal-02153214, hal-02153342, hal-01961496
Contact:
Etienne Andre
Participants:
Etienne Andre, Jaime Eduardo Arias Almeida
Partner:
Loria

6.1.2 Redlog

Name:
Reduce Logic System
Keywords:
Computer algebra system (CAS), First-order logic, Constraint solving
Functional Description:

Redlog is an integral part of the interactive computer algebra system Reduce. It supplements Reduce's comprehensive collection of powerful methods from symbolic computation by supplying more than 100 functions on first-order formulas.

Redlog generally works with interpreted first-order logic in contrast to free first-order logic. Each first-order formula in Redlog must exclusively contain atoms from one particular Redlog-supported theory, which corresponds to a choice of admissible functions and relations with fixed semantics. Redlog-supported theories include Nonlinear Real Arithmetic (Real Closed Fields), Presburger Arithmetic, Parametric QSAT, and many more.
News of the Year:

Parts of the Redlog code are more than 25 years old now. Version 1 of the underlying computer algebra system Reduce has been published even more than 50 years ago. In 2018 we therefore started to go for major revisions and improvements of Redlog's software architecture, which are still under way.

During 2021 we attacked two major workhorses, which are simplification and quantifier elimination by virtual substitution. Recall that our implementations are generic in the sense that they cover the first-order logic part and contain domain-specific black box procedures. They have been frequently extended and modified in the course of multiple research projects throughout the years. The situation had reached a point where a complete reimplementation became necessary, accompanied by a consolidation of numerous experimental options. We finished the generic part of the simplifier, and we are making good progress with the quantifier elimination. Our principal design goal is more simplicity for the sake of better long-term maintainability. Technically we now favor keeping state spaces in explicit mutable data structures rather than on the recursion stack. Although not directly supported by the underlying Lisp system, we use object oriented ideas and approaches to the extent possible.
URL:
https://www.redlog.eu/
Contact:
Thomas Sturm
Participant:
Thomas Sturm

6.1.3 SPASS Workbench

Name:
SPASS Automated Reasoning Workbench
Keywords:
Decision, Linear Systems Solver
Functional Description:
The SPASS Workbench is a collection of tools for various reasoning tasks in logic. It currently comprises the first-order theorem prover SPASS, a decision procedure for linear (mixed) arithmetic SPASS-IQ, and an SMT (Satisfiability Modulo Theory) solver for linear (mixed) arithmetic. In preparation are a SAT solver SPASS-SAT, a propositional CNF converter SPASS-CNF, and a solver SPASS-SPL for a fragment we called SUPERLOG that is the first-order Bernays Schoenfinkel class extended with linear arithmetic.
News of the Year:
We finished the first part of SPASS-SPL that actually does reasoning through a Datalog hammer. Reasoning tasks out of the SUPERLOG language are reduced to reasoning tasks in a classical Datalog language.
URL:
https://www.mpi-inf.mpg.de/departments/automation-of-logic/software/spass-workbench/
Publications:
hal-03531893, hal-03531889, hal-03531894
Contact:
Christoph Weidenbach
Participants:
Martin Bromberger, Christoph Weidenbach

6.1.4 TLAPS

Name:
TLA+ proof system
Keyword:
Proof assistant
Functional Description:
TLAPS is a platform for developing and mechanically verifying proofs about TLA+ specifications. The TLA+ proof language is hierarchical and explicit, allowing a user to decompose the overall proof into proof steps that can be checked independently. TLAPS consists of a proof manager that interprets the proof language and generates a collection of proof obligations that are sent to backend verifiers. The current backends include the tableau-based prover Zenon for first-order logic, Isabelle/TLA+, an encoding of TLA+ set theory as an object logic in the logical framework Isabelle, an SMT backend designed for use with any SMT-lib compatible solver, and an interface to a decision procedure for propositional temporal logic.
News of the Year:
Besides bug fixes, work on the proof manager in 2021 concentrated on the following items:
- proof methods for reasoning about the enabled and action composition operators of TLA+,
- support for reasoning about recursively defined operators,
- and support for tuples in binding constructs such as quantifiers and set comprehension.
A new version of the SMT backend is in preparation, and several changes were made to the Isabelle backend. We expect all these new developments to be consolidated for a major release to appear in 2022.
URL:
https://tla.msr-inria.inria.fr/tlaps/content/Home.html
Contact:
Stephan Merz
Participants:
Damien Doligez, Stephan Merz, Ioannis Filippidis
Partner:
Microsoft

6.1.5 veriT

Keywords:
Automated deduction, Formula solving, Verification
Functional Description:
VeriT is an open, trustable and efficient SMT (Satisfiability Modulo Theories) solver. It comprises a SAT solver, an efficient decision procedure for uninterpreted symbols based on congruence closure, a simplex-based decision procedure for linear arithmetic, and instantiation-based quantifier reasoning.
News of the Year:

Efforts in 2021 have been focused on quantifier handling, higher logic, and better proof production. Achievements in 2021 are essentially around proof production, which makes veriT particularly suitable for integration within skeptical proof assistants.

The veriT solver participated in the SMT competition SMT-COMP 2021http://www.smtcomp.org with good results. In particular, our fast version (tuned for 24s) was among the fastest (besides portfolio approaches) for several logics, in the 24s category.

We target applications where validation of formulas is crucial, such as the validation of TLA+ and B specifications, and work together with the developers of the respective verification platforms to make veriT even more useful in practice. The solver is available as a plugin for the Rodin platform, and it is integrated within Atelier B.

veriT is also a prototype platform for ideas developed within the Matryoshka project, aiming at greater availability of automated reasoning for proof assistants.
URL:
http://www.veriT-solver.org
Contact:
Pascal Fontaine
Participants:
Haniel Barbosa, Pascal Fontaine, Hans-Jörg Schurr, Sophie Tourret
Partner:
Université de Lorraine

7 New results

7.1 Automated and Interactive Theorem Proving

Participants: Jasmin Christian Blanchette, Martin Bromberger, Antoine Defourné, Martin Desharnais, Daniel El Ouraoui, Ioannis Filippidis, Pascal Fontaine, Fajar Haifani, George Krait, Hendrik Leidinger, Lorenz Leutgeb, Stephan Merz, Qi Qiu, Hans-Jörg Schurr, Sorin Stratulat, Sophie Tourret, Vincent Trélat, Marco Voigt, Uwe Waldmann, Christoph Weidenbach.

7.1.1 Contributions to SMT Techniques

Quantifier Handling in First-Order SMT.

Designing techniques for handling quantifiers in SMT has always been an important objective of the team.

Quantifier reasoning in SMT solvers relies on instantiation: ground instances are generated heuristically from the quantified formulas until a contradiction is reached at the ground level. Previous instantiation heuristics, however, often fail in the presence of nested quantifiers. To address this issue we introduced a unification-based method that augments the problem with shallow quantified formulas obtained from assertions with nested quantifiers. These new formulas help unlock the regular instantiation techniques, but parsimony is necessary since they might also be misguiding. To mitigate this, we identified some effective restricting conditions. The method has been implemented in the veriT solver, and tested on benchmarks from the SMT-LIB. It allowed the solver to prove more formulas, faster. This was published at FroCoS 2021, and the paper received the award for the best student paper 35.

Quantifier Handling in Higher-Order SMT.

Joint work with Haniel Barbosa (Univ. Feder. de Miras Gerais, Brazil).

SMT solvers have throughout the years been able to cope with increasingly expressive logics, from ground formulas to full first-order logic (FOL). In the past, we proposed a pragmatic extension for SMT solvers to support higher-order logic reasoning natively without compromising performance on FOL reasoning, thus leveraging the extensive research and implementation efforts dedicated to efficient SMT solving. However, the higher-order SMT solvers resulting from this work are not as effective as we would expect given their performances in first-order logic. We believe this comes from the fact that only the core of the SMT solver has been extended, ignoring in particular the modules for quantifier instantiation.

This motivated us to start working on an extension of the main quantifier-instantiation approach (congruence closure with free variables, CCFV) to higher-order logic in 2020. This work is still ongoing. We are working on an encoding of the CCFV higher-order problem into a set of SAT constraints. In 2020, we concentrated our efforts mainly on the theory, to prove the soundness and completeness of our approach. This year, as a first step towards an implementation, we designed precise pseudocode for all elements of CCFV computation.

Proofs for SMT.

We previously developed a framework for processing formulas in automatic theorem provers, with generation of detailed proofs that can be checked by external tools, including skeptical proof assistants. The main components are a generic contextual recursion algorithm and an extensible set of inference rules. Clausification, Skolemization, theory-specific simplifications, and expansion of `let' expressions are instances of this framework. With suitable data structures, proof generation adds only a linear-time overhead, and proofs can be checked in linear time. We implemented the approach in the SMT solver veriT. This allowed us to dramatically simplify the code base while increasing the number of problems for which detailed proofs can be produced. Our publication at CADE 47 demonstrates the excellent results of our approach, building on our previous work on proof formats for SMT and on proof reconstruction within the proof assistant Isabelle/HOL (e.g., 81). Our proof format was moreover the basis for the standard Alethe format 46, which is now getting adopted by the community.

7.1.2 Automated reasoning techniques beyond SMT

Extensions of a formal framework for automated reasoning.

We are part of a group developing a framework for formal refutational completeness proofs of abstract provers that implement automated reasoning calculi, especially calculi based on saturation such as ordered resolution and superposition.

Last year, we published a framework that fully captures the dynamic aspects of proof search with a saturation calculus. This year, we extended this work in two directions. First, we finished a mechanization of the framework in Isabelle/HOL, including a case study. This research was presented at CPP 2021 50. Second, we extended the work to support clause splitting as supported by superposition provers such as SPASS and Vampire. These provers use a SAT solver (either built-in or off-the-shelf) to explore the search space more efficiently. This extension of the framework was highly nontrivial and revealed some completeness issues with the theorem prover Vampire. This work was presented at CADE 2021 33.

During his master internship, Qi Qiu extended the Isabelle formalization by representations of the main loops of saturation-based theorem provers.

Superposition for full higher-order logic.

In previous work, we designed superposition calculi for two fragments of higher-order logic as stepping stones towards full higher-order logic. We have now designed two more superposition calculi: one to handle native Booleans in first-order logic as well as one for full higher-order logic that builds on all the others, and includes partial application (currying), anonymous functions ( $λ$ -expressions), and native Booleans. The proof system works on $β η$ -equivalence classes of $λ$ -terms and relies on higher-order unification to achieve refutational completeness for Henkin semantics.

We implemented the calculus in the Zipperposition prover. This implementation helped us win the first-place trophy at the CADE ATP System Competition (CASC), ahead of Vampire, in the 2021 edition of the competition. Our own empirical evaluation includes benchmarks from the TPTP (Thousands of Problems for Theorem Provers) and interactive verification problems exported from Isabelle/HOL. The results appear promising and suggest that an optimized implementation inside a competitive prover such as E, SPASS, or Vampire would outperform existing higher-order automatic provers. This research was presented at the CADE 2021 conference 27, 43, 51. The last paper won the best student paper award at the conference.

Relevance of clauses for resolution.

A clause is relevant for a refutation with respect to an unsatisfiable clause set if it occurs in all refutation proofs. It is semi-relevant if it occurs in at least one refutation proof. We have shown that for some clause $C$ the question whether it is semi-relevant can be reduced to the question whether there exists a set-of-support (SOS) refutation whose set of support is the singleton ${C}$ 37. To this end we generalized and finalized the well-known completeness result on SOS resolution 83: SOS resolution is complete if and only if there exists a resolution refutation with one of the clauses out of the SOS 37. The notion of semi-relevance is in particular useful to test the contribution of a clause or formula to a specific consequence.

Well-founded cyclic proofs.

In the past few years, cyclic proofs have been witnessed to be natural and useful tools for dealing with fixpoint logics (logics for reasoning about induction and co-induction). Cyclic proofs are currently considered as being non-wellfounded, mainly because they are viewed as finite/regular representations of (a subclass of) infinite proofs. In spite of this belief, the soundness of some of them can be expressed using well-founded arguments. For example, in the context of first-order logic with inductive definitions, the sequent-based proofs built with the CLKID $^{ω}$ cyclic induction proof system can also be validated using Noetherian (well-founded) induction arguments; the induction ordering is the underlying semantic ordering used to show some global trace condition, mainly ensuring that the steps along the infinite paths from cyclic derivations of false sequents are decreasing. This provides a bridge with the state-of-the-art (formula-based) Noetherian induction reasoning. A paper was published at SCSS 2021 49, and we expect that proof techniques specific to this domain make cyclic reasoning more effective.

Abduction for Description Logics.

Abduction is the process of explaining new observations using background knowledge. It is central to knowledge discovery and knowledge processing and has been intensely studied in various domains such as artificial intelligence, philosophy and logic. In the description logic literature, abduction has received little attention, despite being recognised as important for ontology repair, query update and matchmaking.

As part of his PhD, Fajar Haifani develops a technique for abduction in the lightweight description logic $ℰℒ$ , that specializes in representing subset inclusions and membership. His approach consists in translating the problem to first-order logic to harness the power of the automated deduction tool SPASS to produce prime implicates, i.e., most general consequences, from which the solutions of the abduction problem can be reconstructed. Theoretical results of this work have been presented at the SOQE and XLoKR workshops this year 36.

In a joint work with P. Koopmann, W. Del-Pinto and R. Schmidt, we are also working on an extended version of an earlier work on abduction in the expressive description logic $𝒜ℒ𝒞$ 82.

Proofs for TLA+.

The logic of TLA+ mixes first-order and modal reasoning. In particular, the predicate $e n a b l e d A$ is true of a state $s$ if there exists a state $t$ such that $A$ is true over the pair $(s, t)$ . This predicate is at the basis of reasoning about fairness conditions. We designed methods for reasoning about enabled and implemented them in the TLA+ proof system TLAPS. The most elementary technique consists in replacing the enabled operator with existential quantification over all primed state variables. In order to achieve better automation, we also implemented rules that reflect the monotonicity of enabled with respect to implication, as well as a rewrite system that pushes the enabled operator inward in complex formulas and simplifies the resulting proof obligations. These techniques have been validated using several case studies in formal proof, and they allow us for the first time to mechanically prove liveness properties of TLA+ specifications.

In his PhD work, Antoine Defourné investigates encodings of the non-temporal theory of TLA+ in the input languages of automated theorem provers for first-order and higher-order logic, including SMT solvers and Zipperposition. Preliminary results appeared in a paper published at FroCos 2021 32. The new encodings were applied to TLAPS proofs that establish mutual exclusion for the “deconstructed” Bakery algorithm introduced by Lamport 84, as well as refinement of this algorithm by the distributed state machine from 87. These proofs are available online, and the new encodings led to a significant improvement in the degree of automation.

Verification of an algorithm for computing strongly connected components.

In the course of his research project for École des Mines de Nancy, Vincent Trélat formalizes in Isabelle/HOL an algorithm for computing strongly connected components in a graph presented in Vincent Bloemen's PhD thesis 77 and originally due to Dijkstra. After showing the correctness of the sequential version of the algorithm, the objective is to verify data structures underlying a concurrent implementation.

7.2 Formal Methods for Developing and Analyzing Algorithms and Systems

Participants: Étienne André, Johan Arcile, Martin Bromberger, Zheng Cheng, Horatiu Cirstea, Marie Duflot-Kremer, Engel Escaffre-Lefaucheux, Serguei Lenglet, Pierre Lermusiaux, Benjamin Loillier, Dylan Marinho, Dostonbek Matyakubov, Dominique Méry, Stephan Merz, Pierre-Etienne Moreau, Christoph Weidenbach.

7.2.1 Contributions to Formal Methods of System Design

Simpler Rules for Auxiliary Variables.

Refinement of a specification expressed at a high level of abstraction by a lower-level specification is a fundamental concept in formal system development. A key problem in proving refinement is to demonstrate that suitable values of internal variables of the high-level specification can be assigned to every possible execution of the low-level specification. The standard technique for doing so is to exhibit a refinement mapping where values for these variables are computed for each state, but it is also well known that this technique is incomplete. In joint work with Leslie Lamport (Microsoft Research), we revisit the classic paper 68 that introduced constructions for auxiliary variables in order to strengthen the refinement mapping technique. In particular, we introduce simpler rules for defining prophecy variables and demonstrate how they can be used for proving the correctness of an algorithm implementing a linearizable object. We also show that our constructions of auxiliary variables yield a complete proof method. An article based on this work has been accepted for publication at ACM Transactions on Programming Languages and Systems and will appear in 2022.

Formal Analysis of Critical Interactive Systems.

When interactive systems allow users to interact with critical systems, they are qualified as Critical Interactive Systems. Their design requires the support of different activities and tasks to achieve user goals. Examples of such systems are cockpits, control panels of nuclear plants, medical devices, etc. Such critical systems are very difficult to model due to the complexity of the offered interaction capabilities. We present 20 a formal development methodology for designing interactive applications using a correct-by-construction approach. We propose a refinement strategy based on the model-view-controller (MVC) paradigm to structure and design Event-B formal models of the interactive application. The proposed MVC-based refinement strategy facilitates the development of an abstract model and a series of refined models by introducing the possible modes, controller behaviour and visual components of the interactive application while preserving the required interaction-related safety properties. To demonstrate the effectiveness, scalability, reliability and feasibility of our approach, we use a small example from the automotive domain and real-life industrial case studies from aviation. The entire development is realized in Event-B, and the Rodin tool is used to analyze and verify the correctness of the formalized model.

Integration of Knowledge in Formal Development

System engineering development processes rely on modeling activities that lead to different design models 54 corresponding to different analyses of the system under consideration. Domain engineering 55 plays a central role in the explicitation of domain-related properties. We have finalized a collection 58 of results related to ontologies 57 as well as to the domain of interactive systems. Checking the conformance of a system design to a standard is a central activity in the system engineering life cycle, a fortiori when the system is deemed critical. It ensures that a system or a model of a system faithfully meets the requirements of a specification of a standard, improving the robustness and trustworthiness of the system model. We present 40, 39 a formal framework based on the correct-by-construction Event-B method and related theories for formally checking the conformance of a formal system model to a formalized standard specification by construction. This framework facilitates the formalization of concepts and rules from a standard in the form of an ontology, as well as the formalization of an engineering domain, using an Event-B theory consisting of data types and a collection of operators and properties. Conformance checking is accomplished by annotating the system model with typing conditions. We address an industrial case study borrowed from the aircraft cockpit engineering domain to demonstrate the feasibility and strengths of our approach. The ARINC 661 standard is formalized as an Event-B theory. This theory formally models and annotates the safety-critical real-world application of a weather radar system for certification purposes.

Modeling hybrid systems by refinement.

Whenever continuous dynamics and discrete control interact, hybrid systems arise. As hybrid systems become ubiquitous and more and more complex, analysis and synthesis techniques are in high demand to design safe hybrid systems. This is however challenging due to the nature of hybrid systems and their designs, and the question of how to formulate and reason about their safety problems. Previous work has demonstrated how to extend the discrete modeling language Event-B with support for continuous domains to integrate traditional refinement in hybrid system design. We now propose a strategy 30 that can coherently refine an abstract hybrid system design with safety constraints down to a concrete one, integrated with implementable discrete control, that can behave safely. We demonstrate our proposal on a smart heating system that regulates room temperature between two references.

Certified Semantics Transformations

Any given programming language may come with several semantics definitions, such as big-step, small-step, or even abstract machines, which can be seen as an implementation of a language. They all describe identical behaviors of programs, but each may be better adapted for some purpose: for instance, small-step semantics are better suited to prove subject reduction.

To have access to all kinds of semantics at once, we develop transformations between semantics to be able to generate one from the other at no extra cost for the language designer. We propose a transformation from big-step to small-step semantics and certify its correctness using Coq certificates: for a given input language in big-step, we generate the small-step semantics and a Coq proof script that shows the correspondence between the two semantics. We also develop a certified transformation from big-step to abstract machines 22. Finally, we generate abstract machines in a generic and complete way for non-deterministic languages such as process calculi, for which only ad hoc and partial implementations existed so far.

An Extension of PlusCal for Distributed Algorithms.

In previous work 70, we extended the algorithmic language PlusCal 86 by constructs intended for describing distributed algorithms. In his master internship, Dostonbek Matyakubov consolidated the translator for this PlusCal extension to TLA+ specifications.

7.2.2 Automated Reasoning Techniques for Verification

Static analysis of rewriting systems.

Rewriting is a widely established formalism that is especially well suited for describing program semantics and transformations. In particular, constructor-based term rewriting systems are generally used to illustrate the behaviour of functional language programs. In the context of formal verification, it is often necessary to characterize the shape of the reachable terms of such rewrite systems and, in particular, when performing (program) transformations we often want to eliminate some symbols and, more generally, to ensure that some patterns are absent from the result of the transformation.

We have proposed a method to statically analyse constructor term rewriting systems and to verify the absence of patterns from the corresponding normal forms 31. The approach is non-intrusive and avoids the burden of specifying a specific language to characterize the result of the transformation as the user is simply requested to indicate, for the corresponding functions, the patterns that should be eliminated and the respective pre-conditions for the arguments of the function. If the analysed rewriting system features non-linear right-hand sides, false negatives could be obtained but when the system is confluent, as is the case for deterministic functional programs, and if a strict reduction strategy is used, the method handles also some form of non-linear right-hand sides. The method has been implemented in Haskell and the results in terms of expressiveness and efficiency are very encouraging.

Towards Mechanization and Application of SUPERLOG.

In joint work with the groups of Markus Kroetzsch and Christof Fetzer (Technical University of Dresden), we have introduced a logical fragment called SUPERLOG (Supervisor Logic) that is meant to provide a basis for formalizing abstract control algorithms found in ECUs (Electronical Control Units). The language comes with support for fully automated verification and also for execution 34. Technically, SUPERLOG is an extension of the (Horn) first-order Bernays-Schoenfinkel fragment with arithmetic constraints. It extends the well known SMT fragment by universally quantified variables. In addition to the already developed sound and complete calculus for the SUPERLOG language 78, we have now developed a Datalog hammer: a procedure that reduces universally as well as existentially quantified queries to plain Datalog 28. It outperforms any available state-of-the art technique on SUPERLOG formalizations. The theory is based on the decidability results obtained by Marco Voigt 21.

7.2.3 Parametric timed model checking

Theoretical questions.

In 12, we studied the power of updates in parametric timed automata: we showed that, by adding some restrictions compared to the original model, we can also significantly enhance the syntax (by allowing “updates to parameters”) while ensuring that a crucial problem (the emptiness of the valuation set reaching a given discrete location) remains decidable.

Heuristics and efficient synthesis.

In 23, we proposed new algorithms to synthesize valuations yielding at least one infinite accepting run in a parametric timed automaton. This is important for parametric timed model checking, since the violation of a property (expressed using some logics) can reduce to the existence of such an infinite accepting run.

In 26, we formalized and published (using the GNU GPL license) a library of benchmarks for parametric timed systems, with the ultimate goal to use it in further works studying the efficiency of synthesis algorithms.

Application to security properties.

In 13, we targeted the formalization of attack-fault trees, and proposed a method to formally derive parameter valuations for which an attack-fault tree (involving quantitative constants such as time and costs) is safe or, on the other hand, makes an attack possible.

Application to real-time systems.

In 11, we modeled and verified the system of a flight control launcher from ArianeGroup. Using the formalism of parametric timed automata and the IMITATOR model checker 24, we notably derived safe timing parameter valuations ensuring not only the functional correctness, but also some tight constraints on the tasks and their sequential behavior.

Monitoring of hybrid systems.

Finally, we considered monitoring of hybrid systems: while not strictly speaking model checking, monitoring can provide designers with formal guarantees on some concrete system executions. In 53, we proposed a new technique, where the monitoring algorithm takes advantage of a “bounding model” expressed using hybrid automata, which acts as a light overapproximation of the model. As a consequence, our monitoring algorithm can discard false positives, and provides designers with more accurate guarantees, while allowing for very expressive specifications. Our algorithm was implemented in a toolkit, and it is scalable.

7.3 Verification and Analysis of Dynamic Properties of Biological Systems

Participants: Hamid Rahkooy, Thomas Sturm.

Several major research articles on Real Singularities of Implicit Ordinary Differential Equations, on Reduction of Reaction Network Kinetics to Multiple Timescales, and on Geometric Analysis of Steady State Regimes have been published in scientic journals during the reporting period 19, 18, 16. A discussion of that research is available in last year's report.

Parametric Geometric Analysis of Steady State Regimes.

During the last decades there has been considerable research on “toricity” of various algebraic structures 79, 91. In that general context, it is natural that “toricity” of steady state regimes of ordinary differential equations with polynomial vector fields that describe the kinetics of reaction networks stands for binomiality of the steady state ideal, which in turn corresponds to the steady state variety over the complex numbers. In our foundational, non-parametric, work on Geometric Analysis of Steady State Regimes we introduce an alternative concept of toricity over the real numbers 16. Our real toricity refers directly to the geometric shape of the real variety itself. We argue that our notion of toricity is more adequate than the traditional complex one from a biological point of view. We give detailed algorithms for both the real and the complex approach, along with prototypical implementations, and demonstrate on the grounds of systematic benchmarks on a large set of models from the biomodels.net database 88 that the performance of the real approach does not at all fall behind that of the complex one. Technically, our complex algorithms use Gröbner basis techniques, and our real algorithms use real decision procedures such as SMT solving over QF_NRA or real quantifier elimination procedures.

As the next natural step, we investigated the same problems with parametric reaction rates. This is well motivated, as reaction rates are either measured with limited precision, or estimated often only by order of magnitude. Relevant biological findings should be robust under variations of those parameters; as Feinberg points out that in his excellent textbook: The network itself will be our object of study, not the network endowed with a particular set of rate constants80.

Our generalization over the complex numbers 45 requires the careful use of comprehensive Gröbner bases and corresponding techniques 92. Over the real numbers 44 the presence of parameters exceeds the SMT framework, and we make use of real quantifier elimination methods. We successfully analyze various biological models from the literature. In benchmark series with $n$ -site phosphorylation networks we can (for $n = 5$ ) process models with up to 54 species and 30 parameteric rate constants, which amounts to the elimination of 54 real quantifiers in an 84-dimensional space, arriving at concise scientifically interpretable conditions in the parameters.

8 Bilateral contracts and grants with industry

Participants: Martin Bromberger, Christoph Weidenbach.

8.1 Bilateral contracts with industry

The Max Planck Institute for Informatics (MPI-INF) and Logic 4 Business GmbH (L4B) have signed a cooperation contract. Its subject is the application of automated reasoning methods to product complexity management, in particular in the car industry. MPI-INF is providing software and know-how, L4B is providing real-world challenges. The agreement involves Martin Bromberger and Christoph Weidenbach. The company L4B was successfully sold in 2021 to an industrial partner.

9 Partnerships and cooperations

9.1 International initiatives

9.1.1 Participation in other international programs

ANR-NRF ProMiS

Title:
Provable Mitigation of Side Channel through Parametric Verification
Duration:
2020–2024
Coordinators:
Étienne André, Jun Sun
Partner Institutions:
- Université de Lorraine, France (coordinator)
- École Centrale Nantes, France
- Singapore Management University (coordinator)
- Singapore University of Technology and Design
Team participants:
Étienne André, Johan Arcile, Dylan Marinho
Keywords:
security, formal methods, model checking, timed automata
Summary:
The Spectre vulnerability illustrates the fact that attackers can extract information about private data using a timing attack. It is an example of side channel attacks, where secure information flows through side channels unintentionally. We propose techniques for automatically synthesizing mitigations of side channel attacks using formal verification techniques, by reducing this problem to the parameter synthesis problem of a given formalism. We plan to deliver a fully automated toolkit which can be automatically applied to real-world systems.
More information:
ProMiS Web site

ANR-DFG SYMBIONT

Title:
Symbolic Methods for Biological Networks
Duration:
July 2018–April 2022
Coordinators:
Thomas Sturm and Andreas Weber/Reinhard Klein
Partner Institutions:
- CNRS / LORIA (coordinator)
- Univ. of Lille 1, France
- Univ. of Montpellier, France
- Inria Saclay Île de France (Lifeware), France
- Univ. of Bonn, Germany (coordinator)
- RWTH Aachen (Department of Mathematics and Joint Research Center for Computational Biomedecine), Germany
- Univ. of Kassel, Germany
Team participants:
Hamid Rahkooy, Thomas Sturm
Keywords:
molecular interaction networks, computational models, symbolic methods, tropical geometry, real algebraic geometry
Summary:
SYMBIONT is an international interdisciplinary project, funded by ANR in France and by DFG in Germany under the PRCI program. It includes researchers from mathematics, computer science, systems biology, and systems medicine. Computational models in systems biology are built from molecular interaction networks and rate laws, involving parameters, resulting in large systems of differential equations. The statistical estimation of model parameters is computationally expensive and many parameters are not identifiable from experimental data. The project aims at developing novel symbolic methods, aiming at the formal deduction of principal qualitative properties of models, for complementing the currently prevailing numerical approaches. Concrete techniques include tropical geometry, real algebraic geometry, theories of singular perturbations, invariant manifolds, and symmetries of differential systems. The methods are implemented in software and validated against models from computational biology databases.
More information:
SYMBIONT Web site

9.2 International research visitors

9.2.1 Visits of international scientists

Jaco van de Pol

Status:
professor
Institution of origin:
University of Aarhus
Country:
Denmark
Dates:
16–30 October 2021
Context of the visit:
Collaboration with Étienne André, Dylan Marinho, Stephan Merz
Mobility program/type of mobility:
Invited professor (University of Lorraine)

Deepak Kapur

Status:
professor
Institution of origin:
University of New Mexico
Country:
USA
Dates:
15 November 2021 – 12 January 2022
Context of the visit:
Collaboration with Martin Bromberger, Hendrik Leidinger, Christoph Weidenbach
Mobility program/type of mobility:
Invited professor (MPI-INF)

9.3 European initiatives

9.3.1 Horizon Europe

Matryoshka

Program:
ERC
Title:
Fast Interactive Verification through Strong Higher-Order Automation
Duration:
March 2017 – February 2022
Coordinator:
Jasmin Blanchette
Partner Institutions:
- Vrije Universiteit Amsterdam, The Netherlands (coordinator)
- Inria
- Université de Lorraine, France
Team participants:
Jasmin Blanchette, Antoine Defourné, Pascal Fontaine, Stephan Merz, Hans-Jörg Schurr, Sophie Tourret
Keywords:
interactive theorem proving, automated reasoning, higher-order logic, superposition, SMT solving
Summary:
Proof assistants are increasingly used to verify hardware and software and to formalize mathematics. However, despite some success stories, they remain very laborious to use. The situation has improved with the integration of first-order automatic theorem provers—superposition provers and SMT (satisfiability modulo theories) solvers—but only so much can be done when viewing automatic provers as black boxes. The purpose of Matryoshka is to deliver much higher levels of automation to users of proof assistants by fusing and extending two lines of research: automatic and interactive theorem proving. Our approach is to enrich superposition and SMT with higher-order reasoning in a careful manner, in order to preserve their desirable properties. With higher-order superposition and higher-order SMT in place, we will develop highly automatic provers building on modern superposition provers and SMT solvers, following a novel stratified architecture, and integrate them in proof assistants. Users stand to experience substantial productivity gains: From 2010 to 2016, the success rate of automatic provers on interactive proof obligations from a representative benchmark suite called Judgment Day has risen from 47% to 77%; with this project, we aim at 90%–95% proof automation.
More information:
Matryoshka Web site

9.3.2 Other European programs

ARC

Program:
Erasmus+
Title:
Automated reasoning in the class
Duration:
October 2019 – August 2022
Coordinator:
Isabela Dramnesc
Partner Institutions:
- West University of Timisoara, Romania (coordinator)
- Johannes Kepler University Linz, Austria
- RWTH Aachen, Germany
- Eszterhazy Karoly University, Hungary
- University of Lorraine, France
Team participant:
Sorin Stratulat
Keywords:
computational logic, automated reasoning, education
Summary:
The main objective of the project is to improve the education of computer science students in fields related to computational logic, by creating innovative and advanced learning material that uses automated reasoning and by training a large number of academic staff in using this in a modern way. Thus indirectly the project objectives include the effects of increased software reliability: virus elimination, online safety, better detection of negative online phenomena (fake news, cyberbullying, etc.), and other.

PIAF

Program:
Erasmus+
Title:
Pensée Informatique et Algorithmique au Fondamental / Computational and Algorithmic Thinking in Primary Education
Duration:
September 2018 – August 2021
Coordinator:
Brigitte Denis
Partner Institutions:
- University of Liège, Belgium (coordinator)
- University of Luxembourg, Luxembourg
- Saarland University, Germany
- ESPE Nancy, France
Team participant:
Marie Duflot-Kremer
Keywords:
computational and algorithmic thinking, education, primary school
Summary:
The goal of the PIAF project is threefold: creating a repository of skills related to computational and algorithmic thinking, designing activities aiming at the acquisition of these skills, and evaluating the impact of these activities on primary school children and their computational thinking capacities.

9.4 National initiatives

ANR Project DISCONT

Title:
Correct integration of discrete and continuous models
Duration:
March 2018 – September 2023
Coordinator:
Dominique Méry
Partner Institutions:
- Université de Lorraine (coordinator)
- ENSEEIHT/IRIT, Toulouse
- LACL, Paris Est Créteil
- CLEARSY, Aix-en-Provence
Team participants:
Zheng Cheng, Dominique Méry
Summary:
Cyber-Physical Systems (CPSs) connect the real world to software systems through a network of sensors and actuators that interact in complex ways, depending on context and involving different spatial and temporal scales. Typically, a discrete software controller interacts with its physical environment in a closed-loop schema where input from sensors is processed and output is generated and communicated to actuators. We are concerned with the verification of the correctness of such discrete controllers, which requires correct integration of discrete and continuous models. Correctness should arise from a design process based on sound abstractions and models of the relevant physical laws. The systems are generally characterized by differential equations with solutions in continuous domains; discretization steps are therefore of particular importance for assessing the correctness of CPSs. DISCONT aims at bridging the gap between the discrete and continuous worlds of formal methods and control theory. We will lift the level of abstraction above that found in current bridging techniques and provide associated methodologies and tools. Our concrete objectives are to develop a formal hybrid model, elaborate refinement steps for control requirements, propose a rational step-wise design method and support tools, and validate them based on use cases from a range of application domains.
Keywords:
cyber-physical systems, discrete models, continuous models, refinement, verification, tools
More information:
DISCONT Web site

ANR Project EBRP

Title:
Enhancing EventB and RODIN: EventB-Rodin-Plus
Duration:
January 2020 – January 2024
Coordinator:
Dominique Méry
Partner Institutions:
- INPT-ENSEEIHT/IRIT, Toulouse
- CentraleSupelec / LRI
- Université de Lorraine / LORIA
- Université de Paris-Est Créteil / LACL
- University of Düsseldorf / STUPS
- University of Southampton / School of Electronics and Computer Science
Team participants:
Zheng Cheng, Dominique Méry
Keywords:
formal IDE, theory, proof managementr, cyber-physical systems, discrete models, continuous models, refinement, verification, tools
Summary:
The purpose of EBRP is to enhance Event-B and the corresponding Rodin toolset. This will be done by engaging in some basic research dealing with various mathematical theories that are not currently available in Event-B and Rodin. The development of complex systems usually involves different scientific disciplines and skills. For instance, modeling behaviors and interactions of autonomous systems may require concepts from control theory such as differential equations, communication protocols, resource allocation, access control rules, etc. EBRP targets the definition of extension mechanisms for Event-B rather than defining domain-specific modeling languages, and implementing those mechanisms within Rodin.
More information:
EBRP Web site

ANR Project Formedicis

Title:
Formal methods for the development and the engineering of critical interactive systems
Duration:
January 2017 – July 2022
Coordinator:
David Chemouil
Partner Institutions:
- ONERA, Toulouse (coordinator)
- ENSEEIHT/IRIT, Toulouse
- ENAC, Toulouse
- Université de Lorraine
Team participants:
Horatiu Cirstea, Dominique Méry
Summary:
During the last 30 years, the aerospace domain has successfully devised rigorous methods and tools for the development of safe functionally-correct software. During this process, interactive software has received a relatively lower amount of attention. However, Human-System Interactions (HSI) are important for critical systems and especially in aeronautics: for example, the investigation into the crash of the Rio-Paris flight AF 447 in 2009 pointed out a design issue in the Flight Director interface as one of the original causes of the crash. Formedicis aims at designing a formal hub language, in which designers can express their requirements concerning the interactive behavior that must be embedded inside applications, and at developing a framework for validating, verifying, and implementing critical interactive applications expressed in that language.
Keywords:
critical systems, aeronautics, human-system interaction, system requirements

ANR Project PARDI

Title:
Verification of parameterized distributed systems
Duration:
January 2017 – December 2021
Coordinator:
Philippe Quéinnec
Partner Institutions:
- ENSEEIHT/IRIT, Toulouse (coordinator)
- Université Paris Sud/LRI, Saclay
- Université Nanterre/LIP6, Paris
- Inria Nancy – Grand Est
Team participants:
George Krait, Stephan Merz
Summary:
Distributed systems and algorithms are parameterized by the number of participating processes, the communication model, the fault model, and more generally the properties of interaction among the processes. The project aims at providing methodological and tool support for verifying parameterized systems, using combinations of model checking and theorem proving. VeriDis contributes its expertise on TLA+ and its verification tools, and the integration with the Cubicle model checker is a specific goal of the project.
Keywords:
distributed systems, parameters, communication model, fault model, model checking, theorem proving
More information:
PARDI Web site

DFG Transregional Research Center 248 CPEC

Title:
Foundations of Perspicuous Software Systems.
Duration:
January 2019 – December 2022.
Coordinators:
Holger Hermanns and Raimund Dachselt
Partner Institutions:
- Saarland University (coordinator)
- University of Dresden (coordinator)
- Max Planck Institute for Software Systems, Saarbrücken
Team participants:
Fajar Haifani, Sophie Tourret, Christoph Weidenbach.
Summary:
With cyber-physical technology increasingly impacting our lives, it is very important to ensure that humans can understand them. Systems lack support for making their behaviour plausible to their users. And even for technology experts it is nowadays virtually impossible to provide scientifically well-founded answers to questions about the exact reasons that lead to a particular decision, or about the responsibility for a malfunctioning. The root cause of the problem is that contemporary systems do not have any built-in concepts to explicate their behaviour. They calculate and propagate outcomes of computations, but are not designed to provide explanations. They are not perspicuous. The key to enable comprehension in a cyber-physical world is a science of perspicuous computing.
Keywords:
cyber-physical system, explainability, causal analysis
More information:
Perspicuous Computing Web site

9.5 Regional initiatives

The PhD thesis of Antoine Defourné is partly funded by Région Grand Est.

10 Dissemination

10.1 Promoting scientific activities

10.1.1 Scientific events: organisation

General chair, scientific chair

Étienne André was the general chair of Petri Nets'21 (42nd International Conference on Applications and Theory of Petri Nets and Concurrency, June 2021, France).
Stephan Merz, together with Igor Konnov and Markus Kuppe, chaired the TLA+ Tutorial organized online as a satellite event of DISC 2021.

Member of organizing committees

Pascal Fontaine, Stephan Merz and Christoph Weidenbach are co-organizers of the International Summer School on Verification Techniques, Systems, and Applications (VTSA) that has been organized since 2008 in the Greater Region (Nancy, Saarbrücken, Luxembourg, and Liège). In 2021, VTSA was organized in October in Liège, Belgium.
Sophie Tourret was the publicity chair of the 28th International Conference on Automated Reasoning (CADE-28), that took place virtually.
Sophie Tourret co-chairs the organization of workshops and other satellite events of the 11th International Joint Conference on Automated Reasoning (IJCAR 2022).

10.1.2 Scientific events: selection

Chair of conference program committees

Jasmin Blanchette is co-chair of the program committee of the 11th International Joint Conference on Automated Reasoning (IJCAR 2022).
Dominique Méry was a co-chair of the 19th ACM-IEEE International Conference on Formal Methods and Models for System Design (MEMOCODE'21) 62 and of the 8th International Conference on Rigorous State-Based Methods (ABZ 2021) 61.

Member of conference program committees

Étienne André was a member of the program committees of the 24th International Conference on Fundamental Approaches to Software Engineering (FASE), the 24th ACM International Conference on Hybrid Systems: Computation and Control (HSCC), the 18th International Colloquium on Theoretical Aspects of Computing (ICTAC), the 26th IEEE Pacific Rim International Symposium on Dependable Computing (PRDC), and the 15th Theoretical Aspects of Software Engineering Conference (TASE).
Horatiu Cirstea was a member of the program committee of the 5th International Joint Conference on Rules and Reasoning (RuleML+RR).
Jasmin Blanchette was a member of the program committee of the 13th International Symposium on Frontiers of Combining Systems (FroCoS), the 28th International Conference on Automated Deduction (CADE), the 13th NASA Formal Methods Symposium (NFM), the 12th International Conference on Interactive Theorem Proving (ITP), the 33rd Conference on Computer-Aided Verification (CAV), and the 29th Conference on Computer Science Logic (CSL).
Stephan Merz was a member of the program committees of the 8th International Conference on Rigorous State Based Methods (ABZ), the 41st International Conference on Formal Techniques for Distributed Objects, Components, and Systems (FORTE), the 12th International Conference on Interactive Theorem Proving (ITP), the 15th International Conference on Tests and Proofs (TAP), and the 6th Workshop on Formal Integrated Development Environment (F-IDE),
Sorin Stratulat was a member of the program committees of the International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), the International Conference on Information Assurance and Security (IAS), the Working Formal Methods Symposium (FROM), the International Conference on EUropean Transnational Educational (ICEUTE), and the International Conference on Computational Intelligence in Security for Information Systems (CISIS).
Thomas Sturm was a member of the program committees of the 23rd Conference on Computer Algebra in Scientific Computing (CASC) and the 46th International Symposium on Symbolic and Algebraic Computation (ISSAC).
Sophie Tourret is a program committee board member of IJCAI (2022-2024), and was a member of the program committes of the 30th International Joint Conference on Artificial Intelligence (IJCAI-PRICAI), the 28th International Conference on Automated Deduction (CADE), and the 11th ACM SIGPLAN International Conference on Certified Programs and Proofs (CPP).
Uwe Waldmann was a member of the program committee of the 28th International Conference on Automated Deduction (CADE).
Christoph Weidenbach was a program committee board member of the 13th International Symposium on Frontiers of Combining Systems (FroCos) and the 11th ACM SIGPLAN International conference on Certified Programs and Proofs (CPP).

10.1.3 Journal

Member of editorial boards

Jasmin Blanchette served as editor-in-chief of the Journal of Automated Reasoning.
Dominique Méry is the book review editor of the journal Formal Aspects of Computing.
Thomas Sturm is an editor of the Journal of Symbolic Computation (Elsevier) since 2003 and an editor of Mathematics in Computer Science (Springer) since 2013.
Christoph Weidenbach is an editor of the Journal of Automated Reasoning.

Special issues edited

Thomas Sturm edited two special issues of Mathematics in Computer Science on Computer Algebra in Scientific Computing59, 60.

10.1.4 Invited talks

Stephan Merz gave a colloquium talk at the University of Augsburg (online) on January 14.
Sophie Tourret gave a talk for a team seminar of Deducteam at ENS Saclay on September 10.
Sophie Tourret gave a seminar talk and a part of a tutorial at the Dagstuhl seminar 21371 in September.
Sophie Tourret gave a talk for a student working group at ENS Paris on December 15.

10.1.5 Leadership within the scientific community

Étienne André is a steering committee member of the yearly International Workshop on Synthesis of Complex Parameters.
Dominique Méry is a member of the IFIP Working Group 1.3 on Foundations of System Specifications.
Stephan Merz is a member of the IFIP Working Group 2.2 on Formal Description of Programming Concepts.
Sophie Tourret is a steering committee member of the bi-annual International Workshop on Practical Aspects of Automated Reasoning. She is also the editor of the newsletter of AAR, the Association for Automated Reasoning.
Uwe Waldmann was a member of the committee for the Bill McCune PhD Award in Automated Reasoning.
Christoph Weidenbach is president of CADE. He is also a member of the IJCAR steering committee.

10.1.6 Scientific expertise

Thomas Sturm was a project partner in the Engineering and Physical Sciences Research Council (EPSRC) Projects EP/T015748/1 and EP/T015713/1Pushing Back the Doubly-Exponential Wall of Cylindrical Algebraic Decomposition, Universities of Coventry and Bath, UK.

10.1.7 Research administration

Stephan Merz was a member of the visiting committee of HCERES for evaluating IRISA, Rennes.
Stephan Merz was the delegate for scientific affairs at the Inria Nancy – Grand Est research center and a member of Inria's Evaluation Committee. In 2021, he was the vice-president of the hiring committee of Inria researchers at Inria Nancy.
Stephan Merz is a member of the executive committee of the project on citizens' trust in the digital world (DigiTrust) funded by Lorraine Université d'Excellence.
Uwe Waldmann is ombudsperson of the Max Planck Institute for Informatics.
Christoph Weidenbach is a member of the selection committee of the Saarbrücken Graduate School in Computer Science.

10.2 Teaching - Supervision - Juries

10.2.1 Teaching

DUT 1: Étienne André, Structures de données, 42 HETD, Université de Lorraine – IUT Charlemagne, France.
DUT 1: Étienne André, Interfaces hommes machines, 57 HETD, Université de Lorraine – IUT Charlemagne, France.
DUT 1: Étienne André, Architecture des réseaux, 32 HETD, Université de Lorraine – IUT Charlemagne, France.
DUT 1: Étienne André, Conception orientée objets, 38 HETD, Université de Lorraine – IUT Charlemagne, France.
DUT 2: Étienne André, Projets tuteurés, 14 HETD, Université de Lorraine – IUT Charlemagne, France.
DUT 2: Étienne André, Stages, 42 HETD, Université de Lorraine – IUT Charlemagne, France.
Master: Horatiu Cirstea, Rewriting for proofs and programs, 40 HETD, M2 Informatique and Master Erasmus Mundus DESEM, Université de Lorraine, France.
Master: Horatiu Cirstea, Advanced software engineering, 40 HETD, M2 Informatique and Master Erasmus Mundus DESEM, Université de Lorraine, France.
Master: Horatiu Cirstea, Software engineering & Design patterns, 80 HETD M1 informatique, Université de Lorraine, France.
Licence: Marie Duflot-Kremer, Algorithmes et programmation 1, 60 HETD, L1, Université de Lorraine, France.
Diplôme inter universitaire: Marie Duflot-Kremer, formation d'enseignants du secondaire à la spécialité NSI, 18 HETD, Université de Lorraine, France
Licence: Marie Duflot-Kremer, Accompagnement Algorithmique, 60 HETD, L1, Université de Lorraine, France
Master: Marie Duflot-Kremer and Stephan Merz, Elements of model checking, 40 HETD, M2 Informatique and Master Erasmus Mundus DESEM, Université de Lorraine, France.
Master: Marie Duflot-Kremer and Stephan Merz, Algorithmes distribués, 30 HETD, M1 Informatique, Université de Lorraine, France.
Licence: Engel Escaffre-Lefaucheux, Bases de la Programmation Objets, 10 HETD, L2, Université de Lorraine.
Classe préparatoire universitaire: Engel Escaffre-Lefaucheux, colles Algorithme et Programmation, 12 HETD, Université de Lorraine.
Master: Dominique Méry, Formal Modelling for Software-based Systems 40 HETD, M2 Informatique and Master Erasmus Mundus DESEM, Université de Lorraine, France.
Master: Dominique Méry, Models and algorithms, M1 Telecom Nancy, 48 HETD, Université de Lorraine, France.
Master: Dominique Méry, Formal Modelling for Software-based Systems, M2 Telecom Nancy, 24 HETD, Université de Lorraine, France.
Master: Sophie Tourret, Decision Procedures for Program Verification, guest lecturer for 8 HETD in january 2021, M2 Informatique and Master Erasmus Mundus DESEM, Université de Lorraine, France.
Master: Sophie Tourret, Decision Procedures for Program Verification, 32 HETD in 2021-2022 (winter semester), M2 Informatique and Master Erasmus Mundus DESEM, Université de Lorraine, France.
Master: Uwe Waldmann, Automated Reasoning I, 60 HETD, Universität des Saarlandes, Germany.
Master: Christoph Weidenbach, Automated Reasoning II, Universität des Saarlandes, Germany.

10.2.2 Supervision

HDR: Sorin Stratulat, Noetherian Induction for Computer-Assisted First-Order Reasoning, Université de Lorraine, 29 June 2021 64.
PhD: Daniel El Ouraoui, Methods for Higher-Order reasoning in SMT, Université de Lorraine. Supervised by Jasmin Blanchette, Pascal Fontaine, and Stephan Merz, 11 February 2021 63.
PhD in progress: Antoine Defourné, SMT for TLAPS, Université de Lorraine. Supervised by Jasmin Blanchette, Pascal Fontaine, and Stephan Merz, since March 2019.
PhD in progress: Martin Desharnais, Verification of First-Order Calculi in Isabelle, Universität des Saarlandes. Supervised by Jasmin Blanchette, Sophie Tourret and Christoph Weidenbach, since August 2021.
PhD in progress: Fajar Haifani, Explications in Logic, Universität des Saarlandes. Supervised by Sophie Tourret and Christoph Weidenbach, since November 2019.
PhD in progress: Hendrik Leidinger, SCL in First-Order Logic with Equality, Universität des Saarlandes. Supervised by Christoph Weidenbach, since August 2020.
PhD in progress: Pierre Lermusiaux, Analysis of properties of interactive critical systems, Université de Lorraine. Supervised by Horatiu Cirstea and Pierre-Etienne Moreau, since October 2017.
PhD in progress: Christoph Lüders, On algorithmic reductions of biochemical reaction networks, Universität Kassel, Germany. Supervised by Werner Seiler, Thomas Sturm, Sebastian Walcher, and Andreas Weber $†$ , since June 2015.
PhD in progress: Dylan Marinho, Detecting timing attacks using formal methods, Université de Lorraine. Supervised by Étienne André, since October 2020.
PhD in progress: Hans-Jörg Schurr, Higher-Order SMT, Université de Lorraine. Supervised by Jasmin Blanchette, Pascal Fontaine, and Stephan Merz, since November 2017.

10.2.3 Juries

Étienne André was a reviewer in the PhD committee of Léo Henry (Université Rennes 1).
Horatiu Cirstea was a reviewer in the PhD committee of Nguyen-Nhat-Binh Trinh (Université de Franche-Comté).
Stephan Merz was a reviewer in the PhD committee of Lucas Franceschino (University of Rennes) and the president of the PhD committees of Sylvain Cecchetto (University of Lorraine).
Thomas Sturm was a reviewer and examiner on the PhD committee of Zak Tonks under the supervision of J. H. Davenport, University of Bath, UK.
Uwe Waldmann was a member of the PhD committee of Alexander Bentkamp (VU Amsterdam).

10.3 Popularization

10.3.1 Internal or external Inria responsibilities

Marie Duflot-Kremer is the deputy vice-president for outreach activities in the supervisory council of SIF (Société Informatique de France) and a member of the scientific committee of Fondation Blaise Pascal.
Marie Duflot-Kremer is a member of the jury of the award Prix du Roman Cyber created by ANSSI (the French agency for the security of information systems) for rewarding a novel related to computer science or cyber-security.
Marie Duflot-Kremer is a member of the Interstices editorial board, a Web site launched by Inria that publishes popularization articles.
Christoph Weidenbach is the head of the steering committee of the German Computer Science Competition for High School Students (BWINF) and a co-organizer and the president of the jury of the final round that took place online in September 2021. Stephan Merz was a member of that jury.

10.3.2 Articles and contents

Marie Duflot-Kremer is a member of the Erasmus+ project PIAF (cf. section 9.3) that studies how computational thinking can be introduced in primary education. The project ended in 2021, and she produced several didactical resources (videos explaining competences in computational thinking).
As a member of the French group Informatique Sans Ordinateur, Marie Duflot-Kremer takes part in creating new popularization activities and publishing online documentation to help people reproduce unplugged computer science activities. She also proposed and supervised an internship for 3rd year students to develop, test in classrooms, and promote such activities.

10.3.3 Education

Marie Duflot-Kremer is a member of the CAPES NSI (numérique et sciences informatique) jury, the committee for hiring secondary school teachers and of the steering committee of the future Concours Général Informatique that will reward the best high school students in computer science.

10.3.4 Interventions

Marie Duflot-Kremer gave a presentation at the Science and You conference about the Inria project Chiche! Un scientifique, une classe encouraging high school students imagine their future in (computer) science, and she participated in several meetings with classes for this project.
Marie Duflot-Kremer gave a talk about unplugged computer activities at the regional annual meeting of APMEP (association of math teachers).
Marie Duflot-Kremer gave a talk during an online training about gender issues and the digital sector organized by Académie de Strasbourg.
Marie Duflot-Kremer and Sophie Tourret participated in Fête de la science by supervising a stand animated by students.
Sophie Tourret animated two interventions in the Condorcet high school in Schœneck within the program Chiche! Un scientifique, une classe.

11 Scientific production

11.1 Major publications

1 inproceedingsT.Thomas Bouton, D. C.Diego Caminha B. de Oliveira, D.David Déharbe and P.Pascal Fontaine. veriT: an open, trustable and efficient SMT-solver.Proc. Conference on Automated Deduction (CADE)5663Lecture Notes in Computer ScienceMontreal, CanadaSpringer2009, 151-156
back to text
2 articleM.Martin Bromberger, T.Thomas Sturm and C.Christoph Weidenbach. A complete and terminating approach to linear integer solving.Journal of Symbolic Computation100September 2020, 102-136
HAL DOI back to text
3 incollectionD.Dominique Cansell and D.Dominique Méry. The Event-B Modelling Method - Concepts and Case Studies.Logics of Specification LanguagesMonographs in Theoretical Computer ScienceSpringerFebruary 2008, 33-140
HAL back to text
4 inproceedingsD.Denis Cousineau, D.Damien Doligez, L.Leslie Lamport, S.Stephan Merz, D.Daniel Ricketts and H.Hernán Vanzetto. TLA+ Proofs.18th International Symposium On Formal Methods - FM 20127436Lecture Notes in Computer ScienceParis, FranceSpringer2012, 147-154
back to text
5 articleA.Andreas Dolzmann and T.Thomas Sturm. Redlog: Computer algebra meets computer logic.ACM SIGSAM Bull.3121997, 2-9
back to text
6 articleH.Hassan Errami, M.Markus Eiswirth, D.Dima Grigoriev, W. M.Werner M Seiler, T.Thomas Sturm and A.Andreas Weber. Detection of Hopf bifurcations in chemical reaction networks using convex coordinates.Journal of Computational Physics291March 2015, 279 - 302
HAL DOI
7 articleE.Evgeny Kruglov and C.Christoph Weidenbach. Superposition Decides the First-Order Logic Fragment Over Ground Theories.Mathematics in Computer Science642012, 427-456
8 incollectionS.Stephan Merz. The Specification Language TLA+.Logics of specification languagesMonographs in Theoretical Computer ScienceSpringer2008, 401-452
HAL back to text
9 inproceedingsT.Thomas Sturm and A.Ashish Tiwari. Verification and synthesis using real quantifier elimination.Proc. ISSAC 2011San Jose, United StatesACM PressJune 2011, 329
HAL DOI
10 inproceedingsC.Christoph Weidenbach, D.Dilyana Dimova, A.Arnaud Fietzke, M.Martin Suda and P.Patrick Wischnewski. SPASS Version 3.5.22nd International Conference on Automated Deduction (CADE-22)5663LNAIMontreal, CanadaSpringer2009, 140-145
back to text

11.2 Publications of the year

International journals

11 articleÉ.Étienne André, E.Emmanuel Coquard, L.Laurent Fribourg, J.Jawher Jerray and D.David Lesens. Parametric Schedulability Analysis of a Launcher Flight Control System under Reactivity Constraints.Fundamenta Informaticae1821September 2021, 31-67
HAL DOI back to text
12 articleÉ.Étienne André, D.Didier Lime and M.Mathias Ramparison. Parametric updates in parametric timed automata.Logical Methods in Computer Science172May 2021, 13:1-13:67
HAL DOI back to text
13 articleÉ.Étienne André, D.Didier Lime, M.Mathias Ramparison and M.Mariëlle Stoelinga. Parametric Analyses of Attack-fault Trees.Fundamenta Informaticae1821September 2021, 69 - 94
HAL DOI back to text back to text
14 articleA.Alexander Bentkamp, J.Jasmin Blanchette, S.Simon Cruanes and U.Uwe Waldmann. Superposition for Lambda-Free Higher-Order Logic.Logical Methods in Computer Science1722021
HAL DOI
15 articleA.Alexander Bentkamp, J.Jasmin Blanchette, S.Sophie Tourret, P.Petar Vukmirović and U.Uwe Waldmann. Superposition with Lambdas.Journal of Automated Reasoning657October 2021, 893-940
HAL DOI
16 articleD.Dima Grigoriev, A.Alexandru Iosif, H.Hamid Rahkooy, T.Thomas Sturm and A.Andreas Weber. Efficiently and Effectively Recognizing Toricity of Steady State Varieties.Mathematics in Computer Science152June 2021, 199 - 232
HAL DOI back to text back to text
17 articleJ.Jawher Jerray, L.Laurent Fribourg and É.Étienne André. An Approximation of Minimax Control using Random Sampling and Symbolic Computation.IFAC-PapersOnLine5452021, 265-270
HAL DOI
18 articleN.Niclas Kruff, C.Christoph Lüders, O.Ovidiu Radulescu, T.Thomas Sturm and S.Sebastian Walcher. Algorithmic Reduction of Biological Networks with Multiple Time Scales.Mathematics in Computer Science153September 2021, 499 - 534
HAL DOI back to text back to text
19 articleW. M.Werner M Seiler, M.Matthias Seiß and T.Thomas Sturm. A Logic Based Approach to Finding Real Singularities of Implicit Ordinary Differential Equations.Mathematics in Computer Science152June 2021, 333-352
HAL DOI back to text
20 articleN. K.Neeraj Kumar Singh, Y.Yamine Aït-Ameur, R.Romain Geniet, D.Dominique Méry and P.Philippe Palanque. On the Benefits of Using MVC Pattern for Structuring Event-B Models of WIMP Interactive Applications.Interacting with ComputersMay 2021
HAL DOI back to text
21 articleM.Marco Voigt. Decidable ** First-Order Fragments of Linear Rational Arithmetic with Uninterpreted Predicates.Journal of Automated Reasoning653March 2021, 357-423
HAL DOI back to text

International peer-reviewed conferences

22 inproceedingsG.Guillaume Ambal, S.Sergueï Lenglet and A.Alan Schmitt. Certified Abstract Machines for Skeletal Semantics.CPP 2022 - 11th ACM SIGPLAN International Conference on Certified Programs and ProofsPhiladelphia, United StatesJanuary 2022, 1-13
HAL back to text
23 inproceedingsÉ.Étienne André, J.Jaime Arias, L.Laure Petrucci and J. v.Jaco van de Pol. Iterative Bounded Synthesis for Efficient Cycle Detection in Parametric Timed Automata.Proceedings of the 27th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS 2021)27th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS 2021)Proceedings of the 27th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS 2021)12651virtual, LuxembourgSpringerMarch 2021, 311-329
HAL DOI back to text
24 inproceedingsÉ.Étienne André. IMITATOR 3: Synthesis of Timing Parameters Beyond Decidability.Proceedings of the 33rd International Conference on Computer-Aided Verification (CAV 2021)33rd International Conference on Computer-Aided VerificationLos Angeles/Online, United StatesJuly 2021, 552-565
HAL DOI back to text
25 inproceedingsÉ.Étienne André and A.Aleksander Kryukov. Parametric non-interference in timed automata.Proceedings of the 25th International Conference on Engineering of Complex Computer Systems (ICECCS 2020)ICECCS 2020 - 25th International Conference on Engineering of Complex Computer SystemsIEEE Conference ProceedingsSingapore, SingaporeIEEEMarch 2021
HAL
26 inproceedingsÉ.Étienne André, D.Dylan Marinho and J.Jaco Van De Pol. A Benchmarks Library for Extended Parametric Timed Automata.15th International Conference on Tests and Proofs (TAP 2021)Proceedings of the 15th International Conference on Tests and Proofs (TAP 2021)12740Virtual, NorwaySpringerJune 2021, 39-50
HAL DOI back to text
27 inproceedingsA.Alexander Bentkamp, J.Jasmin Blanchette, S.Sophie Tourret and P.Petar Vukmirović. Superposition for Full Higher-order Logic.Automated Deduction – CADE 28Automated Deduction - CADE 2812699Lecture Notes in Computer SciencePittsburgh, PA / online, United StatesSpringer International PublishingJuly 2021, 396-412
HAL DOI back to text
28 inproceedingsM.Martin Bromberger, I.Irina Dragoste, R.Rasha Faqeh, C.Christof Fetzer, M.Markus Krötzsch and C.Christoph Weidenbach. A Datalog Hammer for Supervisor Verification Conditions Modulo Simple Linear Arithmetic.FroCos 2021 - 13th International Symposium on Frontiers of Combining Systems12941Lecture Notes in Computer ScienceBirmingham, United KingdomSpringer International PublishingSeptember 2021, 3-24
HAL DOI back to text back to text
29 inproceedingsM.Martin Bromberger, A.Alberto Fiori and C.Christoph Weidenbach. Deciding the Bernays-Schoenfinkel Fragment over Bounded Difference Constraints by Simple Clause Learning over Theories.Lecture Notes in Computer ScienceVerification, Model Checking, and Abstract Interpretation - 22nd International Conference, VMCAI 202112597Verification, Model Checking, and Abstract InterpretationCopenhagen/virtuel, DenmarkSpringer International PublishingJanuary 2021, 511-533
HAL DOI back to text
30 inproceedingsZ.Zheng Cheng and D.Dominique Méry. A Refinement Strategy for Hybrid System Design with Safety Constraints.Model and Data Engineering - 10th International Conference, {MEDI}12732Lecture Notes in Computer ScienceTallinn, EstoniaSpringerJune 2021, 3-17
HAL DOI back to text
31 inproceedingsH.Horatiu Cirstea, P.Pierre Lermusiaux and P.-E.Pierre-Etienne Moreau. Static analysis of pattern-free properties.PPDP 2021: 23rd International Symposium on Principles and Practice of Declarative ProgrammingTallinn, EstoniaACMSeptember 2021, 1-13
HAL DOI back to text
32 inproceedingsA.Antoine Defourné. Improving Automation for Higher-Order Proof Steps.Lecture NotesFroCos 2021 - 13th International Symposium on Frontiers of Combining Systems12941Frontiers of Combining Systems-13th International Symposium, FroCoS 2021, Birmingham, UK, September 8–10, 2021, ProceedingsBirmingham, United KingdomSpringerSeptember 2021, 139-153
HAL back to text
33 inproceedingsG.Gabriel Ebner, J.Jasmin Blanchette and S.Sophie Tourret. A Unifying Splitting Framework.Automated Deduction – CADE 28Automated Deduction - CADE 2812699Lecture Notes in Computer SciencePittsburgh, PA / online, United StatesSpringer International PublishingJuly 2021, 344-360
HAL DOI back to text
34 inproceedingsR.Rasha Faqeh, C.Christof Fetzer, H.Holger Herrmanns, J.Jörg Hoffmann, M.Michaela Klauck, M.Maximilian Koehl, M.Marcel Steinmetz and C.Christoph Weidenbach. Towards Dynamic Dependable Systems through Evidence-Based Continuous Certification.ISoLA 2020 - 9th International Symposium On Leveraging Applications of Formal Methods, Verification and ValidationRhodes, GreeceOctober 2021
HAL back to text
35 inproceedingsBest paperP.Pascal Fontaine and H.-J.Hans-Jörg Schurr. Quantifier Simplification by Unification in SMT.FroCos 2021 - 13th International Symposium on Frontiers of Combining Systems12941Lecture Notes in Computer ScienceBirmingham, United KingdomSeptember 2021, 232-249
HAL DOI back to text back to text
36 inproceedingsF.Fajar Haifani, P.Patrick Koopmann and S.Sophie Tourret. Abduction in EL via Translation to FOL.Proceedings of the Second Workshop on Second-Order Quantifier Elimination and Related Topics (SOQE 2021)associated with the 18th International Conference on Principles of Knowledge Representation and Reasoning (KR 2021)Second Workshop on Second-Order Quantifier Elimination and Related Topics (SOQE 2021)3009CEUR Workshop ProceedingsHanoï (online), VietnamNovember 2021, 46-58
HAL back to text
37 inproceedingsF.Fajar Haifani, S.Sophie Tourret and C.Christoph Weidenbach. Generalized Completeness for SOS Resolution and its Application to a New Notion of Relevance.Automated Deduction – CADE 28Automated Deduction - CADE 2812699Lecture Notes in Computer SciencePittsburgh, PA / online, United StatesSpringer International PublishingJuly 2021, 327-343
HAL DOI back to text back to text
38 inproceedingsJ.Jawher Jerray, L.Laurent Fribourg and É.Étienne André. Robust optimal periodic control using guaranteed Euler's method.Proceedings of the 2021 American Control Conference (ACC 2021)ACC 2021 - American Control ConferenceNew Orleans/Virtual, United StatesIEEEMay 2021, 986-991
HAL DOI
39 inproceedingsI.Ismail Mendil, Y.Yamine Aït-Ameur, N. K.Neeraj Kumar Singh, D.Dominique Méry and P.Philippe Palanque. Leveraging Event-B Theories for Handling Domain Knowledge in Design Models.Dependable Software Engineering. Theories, Tools, and Applications. 7th International Symposium, SETTA 2021, Beijing, China, November 25–27, 2021, Proceedings7th International Symposium on Dependable Software Engineering. Theories, Tools, and Applications (SETTA 2021)13071Lecture Notes in Computer ScienceBeijing/Online, ChinaSpringer International Publishing2021, 40-58
HAL DOI back to text
40 inproceedingsI.Ismail Mendil, Y.Yamine Aït-Ameur, N. K.Neeraj Kumar Singh, D.Dominique Méry and P.Philippe Palanque. Standard Conformance-by-Construction with Event-B.Formal Methods for Industrial Critical Systems. 26th International Conference, FMICS 2021, Paris, France, August 24–26, 2021, Proceedings; Lecture Notes in Computer Science (LNCS)26th International Conference on Formal Methods for Industrial Critical Systems (FMICS 2021)12863Formal Methods for Industrial Critical Systems. 26th International Conference, FMICS 2021, Paris, France, August 24–26, 2021, Proceedings ; ISBN 978-3-030-85247-4Paris, FranceSpringer International Publishing2021, 126-146
HAL DOI back to text
41 inproceedingsD.Dominique Méry. Refinement-based Construction of Correct Distributed Algorithms.ICI2ST 2021 - The Second International Conference on Information Systems and Software TechnologiesQuito / Virtual, EcuadorIEEEMarch 2021
HAL
42 inproceedingsBest paperL. P.Louis Penet de Monterno, B.Bernadette Charron-Bost and S.Stephan Merz. Synchronization Modulo k in Dynamic Networks.Stabilization, Safety, and Security of Distributed Systems23rd International Symposium on Stabilization, Safety, and Security of Distributed Systems (SSS 2021)13046Lecture Notes in Computer ScienceGothenburg / online, SwedenSpringer International PublishingNovember 2021, 425-439
HAL DOI back to text
43 inproceedingsV.Visa Nummelin, A.Alexander Bentkamp, S.Sophie Tourret and P.Petar Vukmirović. Superposition with First-class Booleans and Inprocessing Clausification.Automated Deduction – CADE 28Automated Deduction - CADE 2812699Lecture Notes in Computer SciencePittsburgh, PA / online, United StatesSpringer International PublishingJuly 2021, 378-395
HAL DOI back to text
44 inproceedingsH.Hamid Rahkooy and T.Thomas Sturm. Parametric Toricity of Steady State Varieties of Reaction Networks.Computer Algebra in Scientific ComputingComputer Algebra in Scientific Computing (CASC 2021)12865Lecture Notes in Computer ScienceSochi, RussiaSpringer International PublishingAugust 2021, 314-333
HAL DOI back to text
45 inproceedingsH.Hamid Rahkooy and T.Thomas Sturm. Testing Binomiality of Chemical Reaction Networks Using Comprehensive Gröbner Systems.Computer Algebra in Scientific ComputingComputer Algebra in Scientific Computing (CASC 2021)12865Lecture Notes in Computer ScienceSochi, RussiaSpringer International PublishingAugust 2021, 334-352
HAL DOI back to text
46 inproceedingsH.-J.Hans-Jörg Schurr, M.Mathias Fleury, H.Haniel Barbosa and P.Pascal Fontaine. Alethe: Towards a Generic SMT Proof Format (extended abstract).PxTP 2021 - Seventh Workshop on Proof eXchange for Theorem Proving336EPTCSPittsburgh, PA / virtual, United StatesJuly 2021, 49-54
HAL DOI back to text
47 inproceedingsH.-J.Hans-Jörg Schurr, M.Mathias Fleury and M.Martin Desharnais. Reliable Reconstruction of Fine-Grained Proofs in a Proof Assistant.CADE 28 - 28th International Conference on Automated DeductionPittsburgh/Virtual, United StatesJuly 2021
HAL DOI back to text
48 inproceedingsY.Ying Sheng, Y.Yoni Zohar, C.Christophe Ringeissen, J.Jane Lange, P.Pascal Fontaine and C.Clark Barrett. Politeness for the Theory of Algebraic Datatypes (Extended Abstract).Thirtieth International Joint Conference on Artificial Intelligence, IJCAI-21 (Sister Conferences Best Papers)Montreal, CanadaInternational Joint Conferences on Artificial Intelligence OrganizationAugust 2021, 4829-4833
HAL DOI
49 inproceedingsS.Sorin Stratulat. E-Cyclist: Implementation of an Efficient Validation of FOL ID Cyclic Induction Reasoning.SYMBOLIC COMPUTATION FOR SOFTWARE SCIENCE342Electronic Proceedings in Theoretical Computer ScienceLinz, AustriaSeptember 2021, 129--135
HAL back to text
50 inproceedingsS.Sophie Tourret and J.Jasmin Blanchette. A modular Isabelle framework for verifying saturation provers.CPP '21: 10th ACM SIGPLAN International Conference on Certified Programs and ProofsVirtual, DenmarkACM2021, 224-237
HAL DOI back to text
51 inproceedingsBest paperP.Petar Vukmirović, A.Alexander Bentkamp, J.Jasmin Blanchette, S.Simon Cruanes, V.Visa Nummelin and S.Sophie Tourret. Making Higher-Order Superposition Work.Automated Deduction – CADE 28Automated Deduction - CADE 2812699Lecture Notes in Computer SciencePittsburgh, PA, United StatesSpringer International PublishingJuly 2021, 415-432
HAL DOI back to text back to text
52 inproceedingsP.Petar Vukmirović, J.Jasmin Blanchette and M. J.Marijn J H Heule. SAT-Inspired Eliminations for Superposition.21st International Conference on Formal Methods in Computer-Aided Design (FMCAD 2021)New Haven, CT / virtual, United StatesOctober 2021, 231-240
HAL DOI
53 inproceedingsM.Masaki Waga, É.Étienne André and I.Ichiro Hasuo. Model-bounded monitoring of hybrid systems.This is the author (and slightly extended) version of the manuscript of the same name published in the proceedings of the 12th ACM/IEEE International Conference on Cyber-Physical Systems12th ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS 2021)Proceedings of the 12th ACM/IEEE International Conference on Cyber-Physical SystemsNashville, United StatesACMMay 2021
HAL back to text

Scientific book chapters

54 inbookY.Yamine Aït-Ameur, R.Régine Laleau, D.Dominique Méry and N. K.Neeraj Kumar Singh. Towards Leveraging Domain Knowledge in State-Based Formal Methods.12750Logic, Computation and Rigorous Methods: Essays Dedicated to Egon Börger on the Occasion of His 75th BirthdayLecture Notes in Computer ScienceSpringerJune 2021, 1-13
HAL DOI back to text
55 inbookD.Dominique Méry and S.Souad Kherroubi. Contextual Dependency in State-based Modelling.Implicit and explicit semantics integration in proof based developments of discrete systemsSpringerJanuary 2021
HAL DOI back to text
56 inbookN.Nicolas Schnepf, R.Remi Badonnel, A.Abdelkader Lahmadi and S.Stephan Merz. Automated Orchestration of Security Chains Driven by Process Learning.Communication Networks and Service Management in the Era of Artificial Intelligence and Machine Learning1WileyOctober 2021
HAL DOI
57 inbookN. K.Neeraj Kumar Singh, Y.Yamine Aït-Ameur and D.Dominique Méry. Formal Ontological Analysis for Medical Protocols.Implicit and explicit semantics integration in proof based developments of discrete systemsSpringerJanuary 2021
HAL DOI back to text

Edition (books, proceedings, special issue of a journal)

58 bookY.Yamine Aït-Ameur, S.Shin Nakajima and D.Dominique Méry. Implicit and Explicit Semantics Integration in Proof-Based Developments of Discrete Systems.Springer Singapore2021
HAL DOI back to text
59 bookM.Matthew England, F.François Boulier, T.Timur Sadykov and T.Thomas Sturm. Computer Algebra in Scientific Computing 2020.Mathematics in Computer Science153SpringerSeptember 2021
HAL back to text
60 bookM.Matthew England, W.Wolfram Koepf, T.Timur Sadykov, W.Werner Seiler and T.Thomas Sturm. Computer Algebra in Scientific Computing 2019.Mathematics in Computer Science152SpringerJune 2021
HAL back to text
61 proceedingsA.Alexander RaschkeD.Dominique MéryRigorous State-Based Methods-8th International Conference, ABZ 2021, Ulm, Germany, June 9–11, 2021, Proceedings.ABZ 2021 - 8th International Conference on Rigorous State Based Methods12709Lecture Notes in Computer ScienceUlm, GermanySpringer International PublishingJune 2021
HAL DOI back to text
62 proceedingsA.Arunkumar SD.Dominique MéryI.Indranil SahaL.Lijun ZhangMEMOCODE '21: Proceedings of the 19th ACM-IEEE International Conference on Formal Methods and Models for System Design.MEMOCODE '21: 19th ACM-IEEE International Conference on Formal Methods and Models for System DesignVirtuel, ChinaIEEENovember 2021
HAL DOI back to text

Doctoral dissertations and habilitation theses

63 thesisD.Daniel El Ouraoui. Methods for Higher-Order reasoning in SMT.Université de LorraineFebruary 2021
HAL back to text
64 thesisS.Sorin Stratulat. Noetherian Induction for Computer-Assisted First-Order Reasoning.Université de LorraineJune 2021
HAL back to text

Reports & preprints

65 miscM.Małgorzata Biernacka, D.Dariusz Biernacki, S.Serguei Lenglet and A.Alan Schmitt. Non-Deterministic Abstract Machines.January 2022
HAL DOI

Other scientific publications

66 articleM.Matthew England, F.François Boulier, T.Timur Sadykov and T.Thomas Sturm. Foreword, with a Dedication to Vladimir Gerdt.Mathematics in Computer Science153September 2021, 369 - 371
HAL DOI
67 articleM.Matthew England, W.Wolfram Koepf, T.Timur Sadykov, W. M.Werner M Seiler and T.Thomas Sturm. Foreword, with a Dedication to Andreas Weber.Mathematics in Computer Science152June 2021, 173 - 175
HAL DOI

11.3 Cited publications

68 articleM.Martín Abadi and L.Leslie Lamport. The Existence of Refinement Mappings.Theoretical Computer Science812May 1991, 253-284
back to text
69 bookJ.-R.Jean-Raymond Abrial. Modeling in Event-B: System and Software Engineering.Cambridge University Press2010
back to text
70 inproceedingsH.Heba Alkayed, H.Horatiu Cirstea and S.Stephan Merz. An Extension of PlusCal for Modeling Distributed Algorithms.TLA+ Community Event 2020Freiburg (online), GermanyOctober 2020
HAL back to text
71 inproceedingsR.Rajeev Alur, T. A.Thomas A. Henzinger and M. Y.Moshe Y. Vardi. Parametric real-time reasoning.Proc. 25th Annual ACM Symp. Theory of ComputingSan Diego, CA, USAACM1993, 592-601
back to text
72 inproceedingsÉ.Étienne André and J.Jun Sun. Parametric Timed Model Checking for Guaranteeing Timed Opacity.17th International Symposium on Automated Technology for Verification and Analysis (ATVA 2019)Ming-Hsien TsaiTaipei, TaiwanSpringerOctober 2019
HAL back to text
73 articleL.Leo Bachmair and H.Harald Ganzinger. Rewrite-Based Equational Theorem Proving with Selection and Simplification.Journal of Logic and Computation431994, 217-247
back to text
74 bookR.R. Back and J.J. von Wright. Refinement calculus---A systematic introduction.Springer Verlag1998
back to text
75 incollectionC.Clark Barrett, R.Roberto Sebastiani, S. A.Sanjit A. Seshia and C.Cesare Tinelli. Satisfiability Modulo Theories.Handbook of Satisfiability185Frontiers in Artificial Intelligence and ApplicationsIOS PressFebruary 2009, 26825-885
back to text
76 inproceedingsJ. C.Jasmin Christian Blanchette, S.Sascha Böhme and L. C.Lawrence C. Paulson. Extending Sledgehammer with SMT Solvers.23rd International Conference on Automated Deduction (CADE-23)6803Lecture Notes in Computer ScienceSpringer2011, 116--130
back to text
77 phdthesisV.Vincent Bloemen. Strong Connectivity and Shortest Paths for Checking Models.University of TwenteEnschede, The Netherlands2019
back to text
78 miscM.Martin Bromberger, A.Alberto Fiori and C.Christoph Weidenbach. SCL with Theory Constraints.October 2020
HAL back to text
79 articleD.David Eisenbud and B.Bernd Sturmfels. Binomial Ideals.Duke Mathematical Journal841July 1996
back to text
80 bookM.Martin Feinberg. Foundations of Chemical Reaction Network Theory.202Applied Mathematical SciencesSpringer2019
back to text
81 inproceedingsM.Mathias Fleury and H.-J.Hans-Jörg Schurr. Reconstructing veriT Proofs in Isabelle/HOL.PxTP 2019 - Sixth Workshop on Proof eXchange for Theorem Proving301https://arxiv.org/abs/1908.09480Natal, BrazilAugust 2019, 36-50
HAL DOI back to text
82 inproceedingsP.Patrick Koopmann, W.Warren Del-Pinto, S.Sophie Tourret and R. A.Renate A. Schmidt. Signature-Based Abduction for Expressive Description Logics.KR2020, 592--602
back to text
83 articleL.~Wos, G.A.~Robinson and D.F.~Carson. Efficiency and completeness of the set of support strategy in theorem proving.Journal of the ACM1241965, 536--541
back to text
84 articleL.Leslie Lamport. Deconstructing the Bakery to Build a Distributed State Machine.Comm. ACMto appear2022
back to text
85 bookL.Leslie Lamport. Specifying Systems.Boston, Mass.Addison-Wesley2002
back to text
86 inproceedingsL.Leslie Lamport. The PlusCal Algorithm Language.6th Intl. Coll. Theoretical Aspects of Computing (ICTAC 2009)5684Lecture Notes in Computer ScienceKuala Lumpur, MalaysiaSpringer2009, 36-60
back to text
87 articleL.Leslie Lamport. Time, Clocks, and the Ordering of Events in a Distributed System.Commun. ACM2171978, 558--565
back to text
88 articleN.Nicolas Le Novere, B.Benjamin Bornstein, A.Alexander Broicher, M.Melanie Courtot, M.Marco Donizelli, H.Harish Dharuri, L.Lu Li, H.Herbert Sauro, M.Maria Schilstra, B.Bruce Shapiro and others. BioModels Database: A Free, Centralized Database of Curated, Published, Quantitative Kinetic Models of Biochemical and Cellular Systems.Nucleic acids res.34suppl_1January 2006, D689-D691
DOI back to text back to text
89 articleH.Hanl Lee and A.Angelyn Lao. Transmission Dynamics and Control Strategies Assessment of Avian Influenza A (H5N6) in the Philippines.Infectious Disease Modelling32018, 35-59
DOI back to text
90 bookC.Carroll Morgan. Programming from Specifications.2nd editionPrentice Hall1998
back to text
91 bookB.Bernd Sturmfels. Solving Systems of Polynomial Equations.Providence, RIAMS2002
back to text
92 articleV.Volker Weispfenning. Comprehensive Gröbner Bases.Journal of Symbolic Computation141July 1992, 1--29
back to text

VERIDIS - 2021

VERIDIS - 2021

Keywords

Computer Science and Digital Science

Other Research Topics and Application Domains

1 Team members, visitors, external collaborators

Research Scientists

Faculty Members

Post-Doctoral Fellows

PhD Students

Technical Staff

Interns and Apprentices

Administrative Assistants

External Collaborators

2 Overall objectives

3 Research program

3.1 Automated and Interactive Theorem Proving

3.2 Formal Methods for Developing and Analyzing Algorithms and Systems

Model checking

3.3 Verification and Analysis of Dynamic Properties of Biological Systems

4 Application domains

5 Highlights of the year

5.1 Awards

6 New software and platforms

6.1 New software

6.1.1 IMITATOR

6.1.2 Redlog

6.1.3 SPASS Workbench

6.1.4 TLAPS

6.1.5 veriT

7 New results

7.1 Automated and Interactive Theorem Proving

7.1.1 Contributions to SMT Techniques

Quantifier Handling in First-Order SMT.

Quantifier Handling in Higher-Order SMT.

Proofs for SMT.

7.1.2 Automated reasoning techniques beyond SMT

Extensions of a formal framework for automated reasoning.

Superposition for full higher-order logic.

Relevance of clauses for resolution.

Well-founded cyclic proofs.

Abduction for Description Logics.

Proofs for TLA+.

Verification of an algorithm for computing strongly connected components.

7.2 Formal Methods for Developing and Analyzing Algorithms and Systems

7.2.1 Contributions to Formal Methods of System Design

Simpler Rules for Auxiliary Variables.

Formal Analysis of Critical Interactive Systems.

Integration of Knowledge in Formal Development

Modeling hybrid systems by refinement.

Certified Semantics Transformations

An Extension of PlusCal for Distributed Algorithms.

7.2.2 Automated Reasoning Techniques for Verification

Static analysis of rewriting systems.

Towards Mechanization and Application of SUPERLOG.

7.2.3 Parametric timed model checking

Theoretical questions.

Heuristics and efficient synthesis.

Application to security properties.

Application to real-time systems.

Monitoring of hybrid systems.

7.3 Verification and Analysis of Dynamic Properties of Biological Systems

Parametric Geometric Analysis of Steady State Regimes.

8 Bilateral contracts and grants with industry

8.1 Bilateral contracts with industry

9 Partnerships and cooperations

9.1 International initiatives

9.1.1 Participation in other international programs

ANR-NRF ProMiS

ANR-DFG SYMBIONT

9.2 International research visitors

9.2.1 Visits of international scientists

Jaco van de Pol

Deepak Kapur

9.3 European initiatives

9.3.1 Horizon Europe

Matryoshka

9.3.2 Other European programs

ARC

PIAF