2024Activity reportProject-TeamVERIDIS
RNSR: 201020692C- Research center Inria Centre at Université de Lorraine
- In partnership with:CNRS, Université de Lorraine, Max-Planck-Institut für Informatik Saarbrücken
- Team name: Modeling and Verification of Distributed Algorithms and Systems
- In collaboration with:Laboratoire lorrain de recherche en informatique et ses applications (LORIA)
- Domain:Algorithmics, Programming, Software and Architecture
- Theme:Proofs and Verification
Keywords
Computer Science and Digital Science
- A2.1.1. Semantics of programming languages
- A2.1.4. Functional programming
- A2.1.7. Distributed programming
- A2.1.11. Proof languages
- A2.2. Compilation
- A2.4. Formal method for verification, reliability, certification
- A2.4.1. Analysis
- A2.4.2. Model-checking
- A2.4.3. Proofs
- A2.5. Software engineering
- A4.5. Formal methods for security
- A7.2. Logic in Computer Science
- A8.4. Computer Algebra
Other Research Topics and Application Domains
- B6.1. Software industry
- B6.1.1. Software engineering
- B6.3.2. Network protocols
- B6.6. Embedded systems
1 Team members, visitors, external collaborators
Research Scientists
- Stephan Merz [Team leader, INRIA, Senior Researcher]
- Engel Lefaucheux [INRIA, ISFP]
- Thomas Sturm [CNRS, Senior Researcher]
- Sophie Tourret [INRIA, Researcher]
- Uwe Waldmann [Max Planck Society]
- Christoph Weidenbach [Max Planck Society]
Faculty Members
- Julie Cailler [UL, Associate Professor, from Sep 2024]
- Horatiu Cirstea [UL, Professor]
- Marie Duflot-Kremer [UL, Associate Professor]
- Victor Roussanaly [UL, ATER, until Sep 2024]
- Sorin Stratulat [UL, Associate Professor, HDR]
- Martin Vassor [UL, Associate Professor, from Sep 2024]
Post-Doctoral Fellows
- Martin Bromberger [Max Planck Society, until Sep 2024]
- Sibylle Möhle [Max Planck Society, until Jul 2024]
PhD Students
- Thomas Bagrel [UL, CIFRE]
- Ghilain Bergeron [INRIA]
- Alessio Coltellacci [INRIA]
- Sarah Depernet [INRIA, from Oct 2024]
- Martin Desharnais [Max Planck Society]
- Hendrik Leidinger [Max Planck Society]
- Lorenz Leutgeb [Max Planck Society]
- Simon Schwarz [Max Planck Society]
- Mohamed Amine Snoussi [Westinghouse France, CIFRE]
- Vincent Trélat [INRIA]
Interns and Apprentices
- Sarah Depernet [UL, Intern, from Mar 2024 until Aug 2024]
- Terry Tempestini [INRIA, Intern, from Jun 2024 until Jul 2024]
Administrative Assistants
- Juline Brevillet [UL, until Apr 2024]
- Elsa Maroko [CNRS, from May 2024]
- Jennifer Müller [Max Planck Society]
- Cécilia Olivier [INRIA]
Visiting Scientist
- Alistair Finn Hackett [University of British Columbia, from Aug 2024 until Nov 2024]
External Collaborator
- Pascal Fontaine [Univ. Liège]
2 Overall objectives
The VeriDis project team includes members of the Formal Methods department at LORIA, the computer science laboratory in Nancy, and members of the research group Automation of Logic at Max Planck Institut für Informatik in Saarbrücken. It is headed by Stephan Merz and Christoph Weidenbach. VeriDis was created in 2010 as a local research group of Inria Nancy – Grand Est and has been an Inria project team since July 2012.
The objectives of VeriDis are to contribute to advances in verification techniques, including automated and interactive theorem proving, and to make them available for the development and analysis of concurrent and distributed algorithms and systems, based on mathematically precise and practically applicable development methods. The techniques that we develop are intended to assist designers of algorithms and systems in carrying out formally verified developments, where proofs of relevant properties, as well as bugs, can be found with a high degree of automation.
Within this context, we work on techniques for automated theorem proving for expressive languages based on first-order logic, with support for theories (including fragments of arithmetic or of set theory) that are relevant for specifying algorithms and systems. Ideally, systems and their properties would be specified using high-level, expressive languages, errors in specifications would be discovered automatically, and finally, full verification could also be performed completely automatically. Due to the fundamental undecidability of the problem, this cannot be achieved in general. Nevertheless, we have observed important advances in automated deduction in recent years, to which we have contributed. These advances suggest that a substantially higher degree of automation can be achieved over what is available in today's tools supporting deductive verification. Our techniques are developed within trail-based solving and saturation-based reasoning, the two main frameworks of contemporary automated reasoning, of which respectively SMT (Satisfiability Modulo Reasoning) and superposition are the current most prominent examples in first- and higher-order logic. These two frameworks have complementary strengths and weaknesses. Figuring out how and when to make them converge is part of our interests. Techniques developed within the symbolic computation domain, such as algorithms for quantifier elimination for appropriate theories, are also relevant, and are part of our portfolio of techniques. In order to handle expressive input languages, we are working on techniques that encompass tractable fragments of higher-order logic, for example for specifying inductive or co-inductive data types, for automating proofs by induction, or for handling collections defined through a characteristic predicate.
Since full automatic verification remains elusive, another line of our research targets interactive proof platforms. We intend these platforms to benefit from our work on automated deduction by incorporating powerful automated backends and thus raise the degree of automation beyond what current proof assistants can offer. Since most conjectures stated by users are initially wrong (due to type errors, omitted hypotheses or overlooked border cases), it is also important that proof assistants be able to detect and explain such errors rather than letting users waste considerable time in futile proof attempts. Moreover, increased automation must not come at the expense of trustworthiness: skeptical proof assistants expect to be given an explanation of the proof found by the backend prover that they can certify.
Model checking is an established and highly successful technique for verifying systems and for finding errors. Our contributions in this area more specifically target quantitative aspects, in particular the verification of timed or probabilistic systems. A specificity of VeriDis is to consider partially specified systems, using parameters, in which case the verification problem becomes the synthesis of suitable parameter valuations.
Our methodological and foundational research is accompanied by the development of efficient software tools, several of which go beyond pure research prototypes: they have been used by others or have been integrated in verification platforms developed by other groups. We also validate our work on verification techniques by applying them to the formal development of algorithms and systems. We mainly target high-level descriptions of concurrent and distributed algorithms and systems. This class of algorithms is ubiquitous, ranging from multi- and many-core algorithms to large networks and cloud computing, and their formal verification is notoriously difficult. Targeting high levels of abstraction allows the designs of such systems to be verified before an actual implementation has been developed, contributing to reducing the costs of formal verification. The potential of distributed systems for increased resilience to component failures makes them attractive in many contexts, but also makes formal verification even more important and challenging. Our work in this area aims at identifying classes of algorithms and systems for which we can provide guidelines and identify patterns of formal development that makes verification less an art and more an engineering discipline. We mainly target components of operating systems, distributed and cloud services, and networks of computers or mobile devices. When correctness properties have been formally verified for a high-level specification of an algorithm, the correctness of an implementation of an algorithm still remains to be checked, using techniques such as refinement proofs, code generation, testing or trace validation.
Beyond formal system verification, we pursue applications of some of the symbolic techniques that we develop in other domains. We have observed encouraging success in using techniques of symbolic computation for the qualitative analysis of biological and chemical networks described by systems of ordinary differential equations that were previously only accessible to large-scale simulation. Such networks include biological reaction networks as they occur with models for diseases such as diabetes or cancer. They furthermore include epidemic models such as variants and generalizations of SEIR1 models, which are typically used for Influenza A or Covid-19. In this way, we aim for our work grounded in verification to have an impact on the sciences, beyond engineering, which will feed back into our core formal methods community.
3 Research program
3.1 Automated and Interactive Theorem Proving
The VeriDis team gathers experts in techniques and tools for automatic deduction and interactive theorem proving, and specialists in methods and formalisms designed for the development of trustworthy concurrent and distributed systems and algorithms. Our common objective is twofold: first, we wish to advance the state of the art in automated and interactive theorem proving, and their combinations. Second, we work on making the resulting technology available for the computer-aided verification of distributed systems and protocols. In particular, our techniques and tools are intended to support sound methods for the development of trustworthy distributed systems that scale to algorithms relevant for practical applications.
VeriDis members from Saarbrücken are developing the Spass 11workbench. It currently consists of one of the leading automated theorem provers for first-order logic based on the superposition calculus 50, a theory solver for linear arithmetic 2, a CDCL2 based satisfiability solver and a propositional converter to clausal normal form. Recently we have extended it to a Datalog hammer solving universal and existential queries with respect to a Horn Bernays-Schoenfinkel theory modulo linear arithmetic 55, 54.
In a complementary approach to automated deduction, VeriDis members from Nancy work on techniques for integrating reasoners for specific theories. They develop veriT1, an SMT 3 solver that combines decision procedures for different fragments of first-order logic. The veriT solver is designed to produce detailed proofs; this makes it particularly suitable as a component of a robust cooperation of deduction tools.
Finally, VeriDis members design effective quantifier elimination methods and decision procedures for algebraic theories, supported by their efficient implementation in the Redlog5 and Logic1 systems.
An important objective of this line of work is the integration of theories in automated deduction. Typical theories of interest, including fragments of arithmetic, are difficult or impossible to express in first-order logic. We therefore explore efficient, modular techniques for integrating semantic and syntactic reasoning methods, develop novel combination results and techniques for quantifier instantiation. These problems are addressed from both sides, i.e. by embedding decision procedures into the superposition framework or by allowing an SMT solver to accept axiomatizations for plug-in theories. We also develop specific decision procedures for theories such as non-linear real arithmetic that are important when reasoning about certain classes of (e.g., real-time) systems but that also have interesting applications beyond verification.
We rely on interactive theorem provers for reasoning about specifications at a high level of abstraction when fully automatic verification is not (yet) feasible. An interactive proof platform should help verification engineers lay out the proof structure at a sufficiently high level of abstraction; powerful automatic plug-ins should then discharge the resulting proof steps. Members of VeriDis have ample experience in the specification and subsequent machine-assisted, interactive verification of algorithms. In particular, we contribute to the development of methods and tools for verifying properties of specifications written in the TLA+59 language, partly supported by the TLA+ Foundation. Our group in particular develops the TLA+ Proof System where proofs are expressed in a declarative language and that calls upon several automatic backends 4. Trust in the correctness of the overall proof can be ensured when the backends provide justifications that can be checked by the trusted kernel of a proof assistant.
Members of VeriDis formalize a framework in the proof assistant Isabelle/HOL for representing the correctness and completeness of automated theorem provers. This work encompasses proof calculi such as ordered resolution or superposition, as well as concrete prover architectures such as Otter or DISCOUNT loops. It also covers the most recent splitting techniques that bring proof calculi closer to SMT solvers.
3.2 Formal Methods for Developing and Analyzing Algorithms and Systems
Theorem provers are not used in isolation. We are most interested in their support of sound methodologies for modeling and verifying systems. In this respect, members of VeriDis have gained expertise and recognition in making contributions to formal methods for concurrent and distributed algorithms and systems 3, 9, and in applying them to concrete use cases. In particular, the concept of refinement48, 51, 62 in state-based modeling formalisms is central to our approach because it allows us to present a rational (re)construction of system development. An important goal in designing such methods is to establish precise proof obligations, many of which can be discharged by automatic tools. This requires taking into account specific characteristics of certain classes of systems and tailoring the model to concrete computational models. Our research in this area is supported by carrying out case studies for academic and industrial developments. This activity benefits from and influences the development of our proof tools.
In this line of work, we investigate specific development and verification patterns for particular classes of algorithms, in order to reduce the work associated with their verification. We are also interested in applications of formal methods and their associated tools to the development of systems that underlie specific certification requirements in the sense of, e.g., Common Criteria. Finally, we are interested in the adaptation of model checking techniques for verifying actual distributed programs, rather than high-level models.
Today, the formal verification of a new algorithm is typically the subject of a PhD thesis, if it is addressed at all. This situation is not sustainable: algorithm developers and system designers must be able to productively use verification tools for validating their algorithms and implementations. On a high level, the goal of VeriDis is to make formal verification standard practice for the development of distributed algorithms and systems, just as symbolic model checking has become commonplace in the development of embedded systems and as security analysis for cryptographic protocols is becoming standard practice today. Although the fundamental problems in distributed programming are well-known, they pose new challenges in the context of modern system paradigms, including ad-hoc and overlay networks or peer-to-peer systems, and they must be integrated for concrete applications.
Model checking.
The paradigm of model checking is based on automatically verifying properties over a formal model of a system, using mathematical foundations. Model checking, while useful and highly successful in practice, can encounter the infamous state space explosion problem. One direction of VeriDis therefore addresses the efficiency of model checking, by proposing new algorithms or heuristics to speed up analysis. We notably focus on the quantitative setting (time, probabilities), and more specifically on the parametric paradigm where some quantitative constants are unknown, and the goal becomes to synthesize suitable valuations. A recent application of the VeriDis team is that of opacity (in the more general field of cybersecurity), addressed using model checking. The team considers a novel definition of opacity in timed automata, where an attacker has only access to the execution time; several recent works address this direction.
3.3 Verification and Analysis of Dynamic Properties of Biological Systems
The unprecedented accumulation of information in biology and medicine during the last 20 years led to a situation where any new progress in these fields is dependent on the capacity to model and make sense of large data. Until recently, foundational research was concerned with simple models of 2 to 5 ordinary differential equations. The analysis of even such simple models was sufficiently involved that it resulted in one or several scientific publications for a single model. Much larger models are built today to represent cell processes, explain and predict the origin and evolution of complex diseases or the differences between patients in precision and personalized medicine. For instance, the biomodels.net model repository 60 contains thousands of hand-built models of up to several hundreds of variables. Numerical analysis of large models requires an exhaustive scan of the parameter space or the identification of the numerical parameters from data. Both are infeasible for large biological systems because parameters are largely unknown and because of the curse of dimensionality: data, even rich, become rapidly sparse when the dimensionality of the problem increases. On these grounds, VeriDis researchers aim at formal symbolic analysis instead of numerical simulation.
As an illustration of the approach, consider BIOMD0000000716 in the above-mentioned BioModels database, which models the transmission dynamics of subtype H5N6 of the avian Influenza A virus in the Philippines in August 2017 61. This model describes four species (susceptible/infected bird or human) together with their dynamics. Using purely symbolic algorithms, we obtain a decomposition of the dynamics into three subsystems , , and with attractive manifolds , and . The constant factors appearing in the corresponding differential equations indicate that the system is 125 times slower than , and that is another 125 times slower.
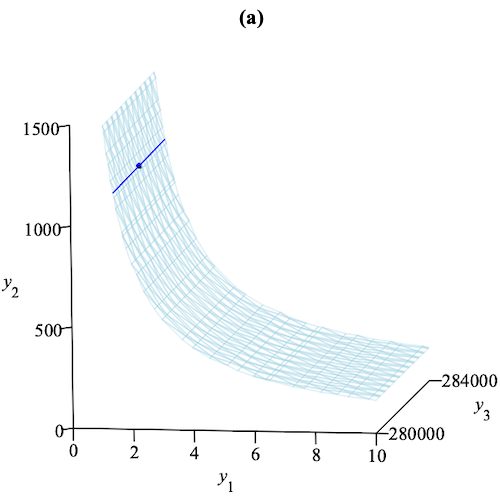
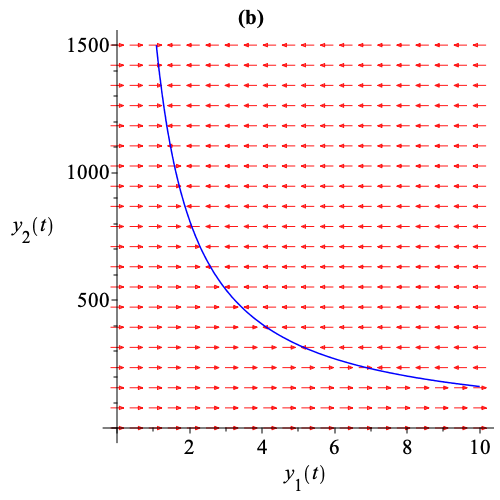
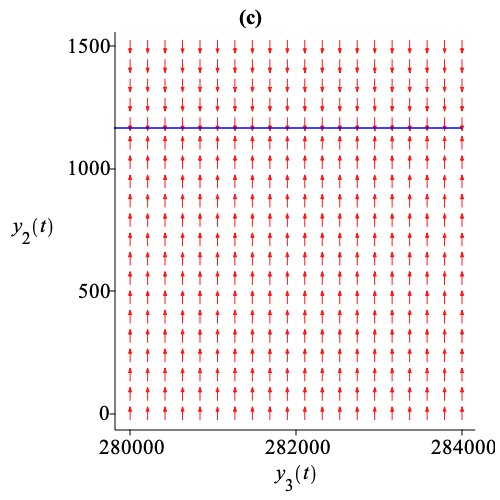
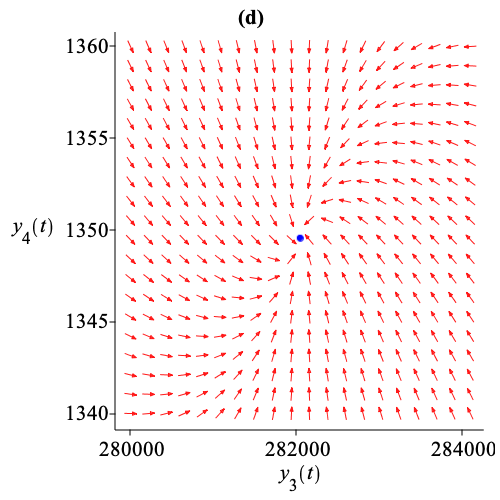
The figure illustrates an epidemic model of avian Influenza A.
The figure illustrates an epidemic model of avian Influenza A.
This multiple time scale reduction emphasizes a cascade of successive relaxations of model variables. Figure 1(a) shows the surface of projected into 3D space, with the line and the dot representing the submanifolds and . Figure 1(b) illustrates the direction field of projected into 2D space. The curve corresponds to , indicating that the population of susceptible birds relaxes and that these variables reach quasi-steady state values. Figure 1(c) represents the direction field of on projected into 2D space. The line corresponds to , showing the relaxation of the population of infected birds. Finally, figure 1(d) shows the direction field of on projected into 2D space. The dot corresponds to , indicating the relaxation of the populations of susceptible and infected humans to a stable steady state.
The computation time is less than a second. The computation is based on massive SMT solving over various theories, including QF_LRA for tropicalizations, QF_NRA for testing Hurwitz conditions on eigenvalues, and QF_LIA for finding sufficient differentiability conditions for hyperbolic attractivity of critical manifolds. Gröbner reduction techniques are used for final algebraic simplification 58. Observe that numerical simulation would not be able to provide such a global analysis of the overall system, even in the absence of symbolic parameters, as is the case in our rather simple example.
4 Application domains
Distributed algorithms and protocols are found at all levels of computing infrastructure, from many-core processors and systems on chip to wide-area networks. We are particularly interested in the verification of algorithms that are developed for supporting peer-to-peer networks or cloud computing services. Computing infrastructure must be highly available and is ideally invisible to the end user, therefore correctness is crucial. One should note that standard problems of distributed computing such as consensus, group membership or leader election have to be reformulated for the dynamic context of these modern systems. We are not ourselves experts in the design of distributed algorithms, but we work together with domain experts on designing formal models of these protocols, and on verifying their properties. These cooperations help us focus on concrete algorithms and ensure that our work is relevant to the distributed algorithm community.
Our work on symbolic procedures for solving polynomial constraints finds applications beyond verification. In particular, we have been working in interdisciplinary projects with researchers from mathematics, computer science, systems biology, and system medicine on the analysis of reaction networks and epidemic models in order to infer principal qualitative properties. Our techniques complement numerical analysis techniques and are validated against collections of models from computational biology.
The team uses extensions of timed automata (such as parametric timed automata 49) as an underlying formalism to solve practical questions. Our work on parametric timed automata is partly motivated by applications in cybersecurity. Foundational decidability results and novel notions of non-interference and opacity for this class of automata allow us, for example, to determine the maximal frequency of attacker actions for the attack to succeed (i.e., so that these actions remain invisible to the external observer). Our contributions give rise to implementations in the Imitator model checker.
5 Highlights of the year
5.1 Awards
Dylan Marinho, a former PhD student of the group, received an award from the Lorraine Academy of Sciences for his PhD thesis Theoretical and algorithmic contributions to the analysis of safety and security properties in timed systems under uncertainty defended in October 2023.
5.2 Events
This year the VERIDIS team was involved in the organization of two major events for the automated theorem proving community that collectively brought together about 200 specialists of the domain from all over the world in Nancy.
The 12th International Joint Conference on Automated Reasoning (IJCAR) was organized in Nancy between the 1st and the 6th of July. IJCAR is the premier international joint conference on all aspects of automated reasoning, including foundations, implementations, and applications, comprising several leading conferences and workshops. IJCAR 2024 brought together the Conference on Automated Deduction (CADE), the International Symposium on Frontiers of Combining Systems (FroCoS), and the International Conference on Automated Reasoning with Analytic Tableaux and Related Methods (TABLEAUX). Stephan Merz, together with Christophe Ringeissen of the PESTO team of the Inria research center at University of Lorraine and Didier Galmiche of the TYPES research group of LORIA, were the conference chairs, and Sophie Tourret was the workshop chair.
The SAT/SMT/AR summer school took place during the week before IJCAR, also in Nancy. Propositional Satisfiability (SAT), Satisfiability Modulo Theories (SMT), and Automated Reasoning (AR) continue to make rapid advances and find novel uses in a wide variety of applications, both in computer science and beyond. The SAT/SMT/AR Summer School aims to bring a select group of students up to speed quickly in this exciting research area. Sophie Tourret was a scientific and local organizer of this event.
6 New software, platforms, open data
6.1 New software
6.1.1 Logic1
-
Keywords:
First-order logic, Quantifier Elimination, Computer algebra system (CAS)
-
Scientific Description:
Version 0.1.0 of Logic1 was released on November 13, 2024, through CondaForge and has already received 300 downloads.
Logic1 0.1.0 offers a robust framework for working with first-order formulas. Its implementations are designed to be generic and parameterized by theories in the sense of first-order logic, currently supporting the theory of Sets and the theory of Real Closed Fields. Included algorithms cover a range of tasks, such as computing normal forms (CNF, DNF, NNF, PNF), simplification, and quantifier elimination.
Comprehensive documentation is available at docs.logic1.eu and on GitHub.
-
Functional Description:
First-order logic recursively builds terms from variables and a specified set of function symbols with specified arities, which includes constant symbols with arity zero. Next, atomic formulas are built from terms and a specified set of relation symbols with specified arities. Finally, first-order formulas are recursively built from atomic formulas and a fixed set of logical operators.
Logic1 focuses on interpreted first-order logic, where the above-mentioned function and relation symbols have implicit semantics, which is not explicitly expressed via axioms within the logical framework. Typical applications include algebraic decision procedures and, more generally, quantifier elimination procedures, e.g., over the real numbers.
- URL:
-
Contact:
Thomas Sturm
-
Participants:
Thomas Sturm, Nicolas Faroß, Lorenz Leutgeb
6.1.2 Redlog
-
Name:
Reduce Logic System
-
Keywords:
Computer algebra system (CAS), First-order logic, Constraint solving, Quantifier Elimination
-
Functional Description:
Redlog is an integral part of the interactive computer algebra system Reduce. It supplements Reduce's comprehensive collection of powerful symbolic computation methods by supplying more than 100 functions on first-order formulas.
Redlog generally works with interpreted first-order logic in contrast to free first-order logic. Each first-order formula in Redlog must exclusively contain atoms from one particular Redlog-supported theory, which corresponds to a choice of admissible functions and relations with fixed semantics. Redlog-supported theories include Nonlinear Real Arithmetic (Real Closed Fields), Presburger Arithmetic, Parametric QSAT (quantified satisfiability solving), and many more.
-
News of the Year:
Future developments will center on the successor system Logic1, while Redlog will remain available and fully supported.
- URL:
-
Contact:
Thomas Sturm
-
Participants:
Thomas Sturm, Andreas Dolzmann, Melanie Achatz, Marek Kosta, Aless Lasaruk, Herbert Melenk, Winfried Neun, Andreas Seidl, Christoph Zengler, Volker Weispfenning
6.1.3 SPASS Workbench
-
Name:
SPASS Automated Reasoning Workbench
-
Keywords:
Decision, Linear Systems Solver
-
Functional Description:
The SPASS Workbench is a collection of tools for various reasoning tasks in logic. It currently comprises the first-order theorem prover SPASS, a decision procedure for linear (mixed) arithmetic SPASS-IQ, a satisfiability modulo theory (SMT) solver for linear (mixed) arithmetic, a propositional satisfiability (SAT) solver SPASS-SAT and a propositional conjunctive normal form converter SPASS-CNF.
-
News of the Year:
We have successfully applied SPASS-SPL to full fledged functional verification of the eBPF language.
- URL:
- Publications:
-
Contact:
Christoph Weidenbach
-
Participants:
Martin Bromberger, Christoph Weidenbach
6.1.4 E-Cyclist
-
Keyword:
Cyclic proofs
-
Functional Description:
Checking the soundness of cyclic induction reasoning for first-order logic with inductive definitions (FOLID) is decidable but the standard checking method is based on an exponential complement operation for Büchi automata. We devised a polynomial method “semi-deciding” this problem in a paper presented at the CiSS2019 conference (Circularity in Syntax and Semantics). E-Cyclist is an extension of the Cyclist prover (http://www.cyclist-prover.org/) that integrates this method. It successfully checked all the proofs included in the Cyclist distribution. The implementation details have been presented at SCSS 2021 (ID HAL: hal-02464242).
- URL:
-
Contact:
Sorin Stratulat
-
Participant:
Sorin Stratulat
6.1.5 TLAPS
-
Name:
TLA+ proof system
-
Keyword:
Proof assistant
-
Functional Description:
TLAPS is a platform for developing and mechanically verifying proofs about specifications written in the TLA+ language. The TLA+ proof language is hierarchical and explicit, allowing a user to decompose the overall proof into proof steps that can be checked independently. TLAPS consists of a proof manager that interprets the proof language and generates a collection of proof obligations that are sent to backend verifiers. The current backends include the tableau-based prover Zenon for first-order logic, Isabelle/TLA+, an encoding of TLA+ set theory as an object logic in the logical framework Isabelle, an SMT backend designed for use with any SMT-lib compatible solver, and an interface to a decision procedure for propositional temporal logic.
-
News of the Year:
In 2024, in addition to various bug fixes, the code was consolidated in preparation of a new release:
- The build processes is now based on dune.
- Support for the Language Server Protocol was implemented, and this allows TLAPS to be used from the TLA+ Virtual Studio Code Extension.
- The default SMT backend is now the one developed as part of Rosalie Defourné's PhD thesis.
- Support for the enabled and action composition operators of TLA+has been merged in to the main branch.
- URL:
-
Contact:
Stephan Merz
-
Participants:
Damien Doligez, Stephan Merz
-
Partner:
Microsoft
6.1.6 veriT
-
Keywords:
Automated deduction, Formula solving, Verification
-
Functional Description:
VeriT is an open, trustable and efficient SMT (Satisfiability Modulo Theories) solver. It comprises a propositional satisfiability (SAT) solver, an efficient decision procedure for uninterpreted symbols based on congruence closure, a simplex-based decision procedure for linear arithmetic, and instantiation-based quantifier reasoning.
-
News of the Year:
The development of veriT stopped in 2024. We are now working on a new platform called modulariT, that will eventually implement all features of veriT, but whose development is more focused on pedagogy and usefulness for testing ideas than efficiency.
We target applications where validation of formulas is crucial, such as proof about specifications written in the B or TLA+ languages, and we work together with the developers of the respective verification platforms to make SMT solvers even more useful in practice. The veriT solver is available as a plugin for the Rodin platform, and it is integrated within Atelier B.
- URL:
-
Contact:
Pascal Fontaine
-
Participants:
Pascal Fontaine, Sophie Tourret
-
Partner:
Université de Lorraine
6.2 New platforms
6.2.1 ODEbase
Participants: Thomas Sturm.
-
Name:
Online Database of Biomodels Involving Ordinary Differential Equations
-
Keywords:
Automated reasoning, Dynamical systems, Interdisciplinary research, Qualitative analysis
-
Scientific Description:
Symbolic Computation and Automated Reasoning allow qualitative answers to biological questions. Qualitative methods analyze dynamical input systems as formal objects, in contrast to investigating only a subset of the state space, as is the case with numerical simulation. A common format used in mathematical modeling of biological processes is the Systems Biology Markup Language SBML. However, symbolic tools and libraries have a different set of requirements for their input data than their numerical counterparts. The use of SBML data in Symbolic Computation and Automated Reasoning requires significant pre-processing that combines automated translation steps with human interaction and expertise. ODEbase provides pre-processed input data derived from established existing biomodels.
-
Functional Description:
SBML, which is technically an XML instance, has been designed as a very liberal format, and contributors of models are primarily researchers whose key expertise resides in natural sciences. This creates a situation where SBML features may be used in unexpected ways. A sound presentation of corresponding models outside the SMBL framework then requires expertise in the life sciences as well as mathematical competence, primarily in algebra and in dynamical systems. Technically we use a set of Python tools, which we have developed for the semi-automatic conversion of SBML models. Since the conversion process is not fully automatic and our resources are limited, we focus on models that we identify as interesting for Symbolic Computation and Automated Reasoning approaches. Our principal source of models is the renowned online database biomodels.net.
-
News of the Year:
ODEbase has more than doubled its citation count during 2024.
- URL:
- Publications:
-
Contact:
Thomas Sturm
-
Partners:
Christoph Lüders (University of Bonn, Germany), Ovidiu Radulescu (University of Montpellier, France).
7 New results
7.1 Automated and Interactive Theorem Proving
7.1.1 Techniques for Automated Deduction
Participants: Martin Bromberger, Julie Cailler, Martin Desharnais, Pascal Fontaine, Hendrik Leidinger, Lorenz Leutgeb, Sibylle Möhle, Sorin Stratulat, Sophie Tourret, Uwe Waldmann, Christoph Weidenbach.
Quantifier Handling in Higher-Order SMT.
Joint work with Haniel Barbosa (Univ. Federal de Minas Gerais, Brazil).
SMT solvers have throughout the years been able to cope with increasingly expressive logics, from ground formulas to full first-order logic (FOL). In the past, we proposed a pragmatic extension for SMT solvers to support higher-order logic reasoning natively without compromising performance on FOL reasoning, thus leveraging the extensive research and implementation efforts dedicated to efficient SMT solving. However, the higher-order SMT solvers resulting from this work are not as effective as we would expect given their performances in first-order logic. We believe this comes from the fact that only the core of the SMT solver has been extended, ignoring in particular the modules for quantifier instantiation.
This motivated us to start working on an extension of the main quantifier-instantiation approach (congruence closure with free variables, CCFV) to higher-order logic in 2020. We are working on an encoding of the CCFV higher-order problem into a set of SAT constraints. In previous years, we concentrated our efforts on the theory, to prove the soundness and completeness of our approach, and developed pseudo-code for all elements of CCFV computation. In 2022 and 2023, these algorithms were implemented in a C++ library, and they were tested on benchmarks from the SMT-lib collection. We started to integrate this library within a new SMT framework. In 2024, most of the work has been focused on building the rest of the infrastructure of the framework. The library will eventually be released under an open-source permissive license.
Effective Symbolic Model Construction.
When automatic reasoning techniques are applied in order to prove a specific property of some system, a proof is a certificate of success. If a proof attempt fails, automatic reasoning techniques may still terminate and implicitly provide a representation of a (counter) model to the property of interest. We have worked on effective representations for such counter models providing insights into why the desired property does not hold. This way, either the system, the formalization of it or the property can be debugged. A prerequisite for such an analysis is the successful termination of the proof attempt. We are working on new techniques for termination in the presence of loops while preserving our capabilities in analyzing the resulting model representations.
SCL Clause Learning from Simple Models.
We have continued our work on the SCL family of automated reasoning calculi. Given a finite consistent set of first-order ground literals without equality, we have developed an algorithm that generates a complete first-order logic interpretation, i.e., an interpretation for all ground literals over the signature and not just those in the input set, that is also a model for the input set. The interpretation is represented by first-order linear literals. It can be effectively used to evaluate clauses. A particular application are SCL stuck states. The SCL (Simple Clause Learning) calculus always computes with respect to a finite number of ground literals. It then finds either a contradiction or a stuck state being a model with respect to the considered ground literals. Our algorithm builds a complete literal interpretation out of such a stuck state model that can then be used to evaluate the clause set. If all clauses are satisfied an overall model has been found. If it does not satisfy some clause, this information can be effectively explored to extend the scope of ground literals considered by SCL 24.
In case of first-order logic with equality, an efficient evaluation of clauses and literals with respect to a set of (ground) unit equations is required for SCL(EQ). To this end we have lifted the classical congruence closure algorithm to the case of equations with variables 46.
Destructive Equality Resolution.
Bachmair's and Ganzinger's abstract redundancy concept for the Superposition Calculus justifies almost all operations that are used in superposition provers to delete or simplify clauses, and thus to keep the clause set manageable. Typical examples are tautology deletion, subsumption deletion, and demodulation, and with a more refined definition of redundancy, joinability and connectedness can be covered as well. The notable exception is Destructive Equality Resolution, that is, the replacement of a clause where by . This operation is implemented in state-of-the-art provers such as E, and it has been shown to be useful in practice: it increases the number of problems that E can solve and it also reduces E's runtime per solved problem. Little was known about how it affects refutational completeness, though (except for the special case that is also a variable). We have demonstrated on the one hand that the naive addition of Destructive Equality Resolution to the standard abstract redundancy concept renders the calculus refutationally incomplete. On the other hand, we have presented several restricted variants of the Superposition Calculus that are refutationally complete even with Destructive Equality Resolution 37.
Guiding Word Equation Solving using Graph Neural Networks.
Joint work with Parosh Aziz Abdulla, Mohamed Faouzi Atig, Chencheng Liang (Univ. of Uppsala, Sweden), Philipp Rümmer (Univ. of Uppsala, Sweden & Univ. of Regensburg, Germany).
Reasoning within theories such as arithmetic, arrays, and algebraic data structures has become a key challenge in automated reasoning. To address this, Satisfiability Modulo Theories (SMT) solvers have been developed, offering efficient decision procedures for a wide range of theories, including string theory. Strings, as a fundamental data type in programming, are crucial for many domains like text processing, database management, and web applications. One of the simplest string constraints is the word equation, modeled as equations in a free semigroup. Although the word equation problem is decidable and lies within PSPACE, SMT solvers often struggle with proving the unsatisfiability of word equations.
We developed a new algorithm that leverages a Graph Neural Network (GNN)-guided approach for solving word equations, building upon the well-known Nielsen transformation for equation splitting. The algorithm iteratively rewrites the terms on both sides of an equation, generating a tree-like search space. The choice of path at each split point significantly impacts solving efficiency, motivating the use of GNNs to make informed decisions about splits. Split decisions are formulated as multi-classification tasks, and five distinct graph representations of word equations are introduced to capture their structural properties for GNN processing.
The algorithm is implemented in a solver named DragonLi. Experimental results on both artificial and real-world benchmarks demonstrate that DragonLi excels in solving satisfiable problems. For single-word equations, DragonLi significantly outperforms well-established string solvers, while for conjunctions of multiple word equations, it remains competitive with state-of-the-art solvers.
Decision procedures for fragments with arithmetic.
Joint work with Bernard Boigelot and Baptiste Vergain (ULiège)
Arithmetic reasoning is an important aspect of automated deduction applied to verification. Fragments mixing arithmetic and uninterpreted symbols are often undecidable. We study the decidability frontier of such fragments. In particular, we are examining monadic first-order logic with order interpreted over the real numbers. This fragment is decidable, whereas adding the successor (or more precisely the “”) function is undecidable. Although this result has been known for some time, no effective decision procedure exists. We want to develop an effective procedure, first, because a fundamental understanding of this fragment is scientifically interesting, and second, because this deep understanding can be inspirational for new SMT quantifier instantiation techniques in the presence of arithmetic. We designed and published one key element of this decision procedure, namely the emptiness test of automata on linear orderings 23.
7.1.2 Integration of automated and interactive theorem proving
Participants: Julie Cailler, Alessio Coltellacci, Martin Desharnais, Stephan Merz, Sorin Stratulat, Vincent Trélat, Sophie Tourret, Uwe Waldmann.
Integration of Abduction in Isabelle/HOL.
Joint work with Haniel Barbosa (Univ. Federal de Minas Gerais, Brazil).
Thanks to the creation of the associate team Carma (cf. section 9.1), Sophie Tourret and Haniel Barbosa have started to work on a new collaborative project. Its objective is the integration of CVC5's abduction mechanism into the proof assistant Isabelle/HOL. Abduction is a logical operation that provides tentative explanations to statements in a given theory. For a proof assistant, it could be turned into a tool that suggests missing hypotheses or intermediary steps in proofs. CVC5 is currently the best tool for abduction modulo theories, and Isabelle/HOL is the proof assistant with the best automation. By combining both into a prototype tool, we want to identify robustly the bottlenecks of abduction and address them until abduction becomes useful in practice to help proof engineers.
Extensions of a Formal Framework for Automated Reasoning.
Joint work with Balazs Toth, a PhD student of Jasmin Blanchette in Munich.
We are part of a group developing a framework for formal refutational completeness proofs of abstract provers that implement automated reasoning calculi, especially calculi based on saturation such as ordered resolution and superposition. In previous work, we formalized in Isabelle/HOL a framework that fully captures the dynamic aspects of proof search with a saturation calculus.
This year, we completed the formalization in Isabelle/HOL of the superposition calculus, a state-of-the-art technique for theorem proving in first-order logic and higher-order logic with equality. The calculus was formalized to be compatible with the framework. The results were presented at the conference ITP 2024 28.
Proof Translation from HOL Light to Isabelle/HOL.
Joint work with Lawrence Paulson (Univ. of Cambridge).
We revived an existing technique for the automatic translation of proofs in the proof assistant HOL-Light to proofs in Isabelle/HOL with the help of Stéphane Glondu, an Inria engineer. Our target was a proof of the compactness of first-order logic. Whereas the update of the existing method went well (and was presented at the Isabelle Workshop 2024), we deemed the way the results are used in Isabelle/HOL to be unsatisfactory. We therefore worked in parallel on a manual translation of the existing HOL-Light proof with the help of Lawrence Paulson. This translation is complete and will soon be submitted to the Archive of Formal Proofs, the main repository for Isabelle/HOL proofs.Reconstruction of SMT Proofs.
Joint work with Bruno Andreotti and Haniel Barbosa (Univ. Federal de Minas Gerais, Brazil), and with Gilles Dowek (Inria Deducteam).
SMT solvers are widely considered as the tools of choice for program and system verification. Their combination with skeptical proof assistants requires proofs found by SMT solvers to be certified by the trusted kernel of proof assistants. The Alethe format represents a trace of an SMT proof, explaining why a set of SMT constraints is unsatisfiable. In this work, we describe how to interpret Alethe proof traces and generate corresponding proofs that are accepted by the Lambdapi proof checker, a foundational proof assistant based on dependent type theory and rewriting rules that is intended to serve as a pivot for exchanging proofs between interactive proof assistants. Our implementation currently handles the pure logic (UL) fragment of SMT-LIB; is based on the Carcara proof elaborator and proof checker in order to eliminate need for proof search required for handling some of the coarse-grained rules that exist in Alethe. Particular care has been taken to support efficient reconstruction of the hyper-resolution rule that accounts for the bulk of ground reasoning in Alethe. A preliminary description of our approach was published at the SMT workshop 2024 27, and an extended version of that paper has been submitted to a journal.
Towards a Verified Encoding of Proof Obligations.
The B and Event-B methods for formal system development are widely used for developing certified embedded systems, in particular in the railway domain. Their application generates a high number of proof obligations that must be discharged in order for a system development to be acceptable for certification authorities. Since a high degree of proof automation is essential in an industrial context, proofs are routinely delegated to automatic theorem provers, including SMT solvers. In a recent experiment conducted by the Clearsy company, among the roughly 77,000 proof obligations of a representative development project, 64% were proved automatically by the Atelier B tool suite, leaving 28,000 obligations to be proved by human interaction. The existing encoding of B proof obligations for SMT solvers 57 systematically reduces formulas to first-order logic, eliminating all constructs of set theory. A drawback of this approach is that it destroys the structure of formulas, in particular for constructs such as set comprehension that involve binders. In this work, we develop an alternative encoding that takes advantage of recent capabilities of SMT solvers to handle fragments of higher-order logic. Preliminary experiments suggest that this approach may result in better automation, which can be improved further by designing custom instantiation heuristics. We also aim for a high degree of confidence in the encoding and rely on a definition of the mathematical theory of the B language in the Lean proof assistant, together with a verified translation to SMT-LIB developed in Lean.
Deskolemization.
Joint work with Richard Bonichon (O(1) Labs), Olivier Hermant (CRI, Mines Paris, PSL University, Paris, France), and Johann Rosain (ENS Lyon, Lyon, France)
We present a general strategy that enables the translation of tableau proofs using different Skolemization rules into machine-checkable proofs. It is part of a framework that enables (i) instantiation of the strategy into algorithms for different sets of tableau rules (e.g., different logics) and (ii) easy soundness proof which relies on the local extensibility of user-defined rules. Furthermore, we propose an instantiation of this strategy for first-order tableaux that handles notably pre-inner Skolemization rules, which is, as far as the authors know, the first one in the literature. This deskolemization strategy has been implemented in the Goéland automated theorem prover, enabling an export of its proofs to Coq and Lambdapi. Finally, we have evaluated the algorithm performances for inner and pre-inner Skolemization rules through the certification of proofs from some categories of the TPTP library
An Extension of the TPTP Derivation Format for Sequent-Based Calculus.
Joint work with Simon Guilloud (EPFL, Switzerland).
Motivated by the transfer of proofs between proof systems, and in particular from first order automated theorem provers (ATPs) to interactive theorem provers (ITPs), we specify an extension of the TPTP derivation text format to describe proofs in first-order logic: SC-TPTP. To avoid multiplication of standards, our proposed format over-specifies the TPTP derivation format by focusing on sequent formalisms. By doing so, it provides a high level of detail, is faithful to mathematical tradition, and covers multiple existing tools and in particular tableaux-based strategies. We make use of this format to allow the Lisa proof assistant to query the Goéland automated theorem prover, and implement a library of tools able to parse, print and check SC-TPTP proofs, export them into Coq files, and rebuild low-level proof steps from more complex steps.
7.2 Formal Methods for Developing and Analyzing Algorithms and Systems
7.2.1 Contributions to Formal Methods of System Design
Participants: Thomas Bagrel, Ghilain Bergeron, Martin Bromberger, Horatiu Cirstea, Dominique Méry, Stephan Merz, Pierre-Etienne Moreau, Simon Schwarz, Martin Vassor, Christoph Weidenbach.
Effective Execution and Verification.
For certain first-order logic fragments combined with theories, effective symbolic execution and automated verification can be obtained. We propose a translation from eBPF (extended Berkeley Packet Filter) code to CHC (Constrained Horn Clause sets) over the combined theory of bitvectors and arrays. eBPF is in particular used in the Linux kernel where user code is executed under kernel privileges. In order to protect the kernel, a well-known verifier statically checks the code for any harm and a number of research efforts have been performed to secure and improve the performance of the verifier. Our translation procedure bpfverify is precise and covers almost all details of the eBPF language. Functional properties are automatically verified using z3. We prove termination of the procedure and show by real world eBPF code examples that full-fledged automatic verification is actually feasible 25.
Synthesis of inductive invariants for distributed algorithms.
Joint work with Aman Goel (Amazon) and Karem Sakallah (University of Michigan).
We investigate the use of symbolic model checking techniques for automatically computing inductive invariants for parameterized distributed algorithms. Specifically, the IC3PO model checker applies the well-known IC3 model checking algorithm to finite instances of the algorithm and, in case of success, retrieves inductive invariants for those instances. It then inspects these invariants for symmetries with respect to space (processes) and time (e.g., ballot numbers used during the algorithm) and expresses those symmetries by introducing quantifiers. The resulting formulas are then checked for larger input sizes until no new invariants are inferred. In 2024, we worked on extending the technique for specifications that require more expressive logical languages than previously considered. Specifically, we worked on inferring inductive invariants for the well-known Raft consensus algorithm that requires reasoning over sequences. We have so far been able to infer inductive invariants establishing two of the three main correctness properties of Raft.
Verifying and testing graph-based models.
Joint work with Hao Wu and Thomas Flinkow (Maynooth University).
The Event-B formalism is mainly used for modelling reactive systems and requires techniques and tools for validation. In a joint work, we have experimented a new tool called Cyclone that can be used for verifying and testing graph-based models. In contrast to other verification tools, Cyclone provides users with a unique way of building models and specifying their properties, by explicitly constructing and reasoning about graphs. As graphs can naturally capture both static and dynamic behaviours of a system, this allows users to represent many challenging problems. In 38, we describe Cyclone's basic features through different examples. Our preliminary evaluation results show that Cyclone has a promising potential in handling verification tasks from various domains and good usability for those who are not familiar with using verification tools.
Checking contracts in Event-B
The paper 36 reports on some lessons learnt from introducing the use of automated tools for verifying software-based systems such as Event-B and Rodin in higher education at the master's level. The verification of program properties such as partial correctness or absence of errors at runtime is based on induction principles using algorithmic techniques for checking statements in a logical framework such as classical logic or temporal logic. Alan Turing was undoubtedly the first to annotate programs and to apply an induction principle to transition systems. Our work is placed in this perspective of verifying safety properties of programs that could be executed sequentially or in a distributed manner, with the aim of presenting them as simply as possible to student classes in the context of a posteriori verification. We report on an experiment using the Event-B language and associated tools as an assembly and disassembly platform for correcting programs in a programming language. We have adopted a contract-based approach to programming, which we are implementing with Event-B. A few examples are given to illustrate this pedagogical approach as well as comments and observations. This step is part of a process of learning both the underlying techniques and other tools such as Frama-C based on the same ideas.
Verified Code Generation from PlusCal Programs.
Specifications written in high-level languages such as TLA+ are useful for verifying correctness properties. They often result in state spaces that remain manageable for model checking, and they allow users to design inductive invariants that underlie deductive system verification. However, there is a substantial gap between high-level specifications of algorithms and implementations of those algorithms in actual programs. One way to avoid this gap is to translate specifications into code in a programming language that can be compiled and executed. In this work, we investigate the feasibility of such an approach for algorithms written in PlusCal, an algorithmic language that can be translated to TLA+ for verification. We define a series of PlusCal fragments together with semantics-preserving translations from one fragment to the next one, and then aim at implementing a code generator for the most restrictive fragment. In order to ensure the correctness of the approach, the semantics of the intermediate and the target languages is defined in the Lean proof assistant, and the preservation of the semantics by the translations, also defined in Lean, is formally proved.
Validating traces of distributed systems.
Joint Work with Markus Kuppe (Microsoft Research) and Benjamin Loillier (PIXEL team).
Programming distributed systems is error-prone, and while formal methods such as TLA+ can help design such systems, the translation from the verified specification towards the final implementation is rarely certified. In order to bridge the gap between formal specifications of algorithms that are at the core of distributed systems and actual implementations of these systems, we developed a framework for the instrumentation of Java programs allowing one to record events and variable updates that are meaningful at the level of a given TLA+ specification. We then use the TLA+ model checker to verify that the recorded trace of an execution indeed corresponds to a possible execution of the high-level specification. Although this approach cannot formally establish the correctness of an implementation, experience with applying it to several distributed algorithms, including a production system that had been extensively validated using traditional testing techniques, indicates that it is surprisingly effective at discovering discrepancies between the TLA+ specification and the implementation. We describe the technique and discuss reasons for these discrepancies in a paper published at SEFM 2024 26. A journal version of that paper is in preparation.
Reversibility for Fault Tolerance in Typed Sessions.
Joint work with Adam Barwell (University of St. Andrews, Scotland) and Ping Hou (University of Oxford, England).
Multiparty Session Types (MPST) are a family of type-based techniques developed to prevent various classes of bugs in message-passing concurrent programs, such as the absence of deadlock. MPST are also used as a form of protocol specification, where the well-typedness of a program ensures its conformance to the specification (session fidelity). However, MPST often assume a reliable model of communication, i.e. without message loss or process faults, and existing approaches to relax this assumption either augment MPST with additional elements to deal with faults (e.g. placing explicit checkpoints in the protocol specification), or lower the guarantees provided (e.g. Affine MPST, which safely stop the whole system in case of a process failure, losing session fidelity).
In this project, we aim to implement MPST on top of a reversible variant of the higher-order -calculus. In such a setting, upon failure of a process, we expect the system to transparently revert to a previous state, thus recovering from the failure. Contrary to existing approaches based on reversibility, we do not modify the syntax or the semantics of MPST, allowing users to transparently switch from standard MPST to fault-tolerant MPST.
7.2.2 Model checking for stochastic, timed or linear systems
Participants: Sarah Depernet, Marie Duflot-Kremer, Engel Lefaucheux, Stephan Merz, Amine Snoussi.
Opacity of timed automata.
Joint work with Étienne André (University Paris Sorbonne Nord).
Opacity of a system is a property describing the impossibility for an external attacker to deduce some private information by observing an execution of the system. This notion is known 56 to be undecidable in the general case, as such, most works consider restricted frameworks. In 40, we considered a variety of opacity problems by weakening either the model or the attacker. Specifically, we considered limitations on the number of clocks, the diversity of observations provided by the system, and the number of observations the attacker could access, among other restrictions.
The idea of limiting the attacker's power can be seen as an extension to an existing line of research where the attacker only has access to the entire duration of the executions. In 20 and 21 we also studied this variant of opacity. In 20, we considered timed automata with a single clock, while allowing parameters. We developed a method to compute the set of private and public durations observable by the attacker, as well as to compare those two sets when feasible. In 21, we considered systems with arbitrarily many clocks, excluded parameters, and introduced a form of control to the system. The objective was to detect when a system could be easily modified to ensure opacity.
Diagnosis of stochastic systems.
The notion of diagnosis can be seen as a dual to opacity. While opacity seeks to hide private information from an observer, diagnosis aims to provide information about specific unobservable behaviors of a system, such as failures. The study of diagnosis in stochastic systems, such as those based on Markov chains, is now well-developed. For instance, in 53, the authors demonstrate, for various forms of diagnosis, how to determine whether a system is diagnosable and, if so, how to construct a diagnoser, i.e., a tool that translates a sequence of observations into a verdict. In 32, we examined how to minimize the cost of diagnosis. This included reducing both the delay between a fault's occurrence and its detection by the diagnoser, as well as reducing the number of sensors, and the frequency of their usage.
Modeling and verifying the Bitbus protocol.
Bitbus is a standard protocol used in master-slave networks of industrial controllers. In the context of a project aimed at reingeneering protocols based on Bitbus that are used in nuclear power plants, we model the protocol as communicating timed automata with the objective of studying some of the properties it guarantees, in particular with respect to the tolerance of intermittent faults.
Termination of linear loops.
Loops are a fundamental component of any programming language, and their study plays a crucial role in several subfields of computer science, including automated verification, abstract interpretation, program analysis, semantics, and more. Significant work in the linear dynamical systems community has focused on representing program loops as linear systems and analyzing the properties they satisfy, particularly with regard to loop termination. Since determining the termination of linear dynamical systems is undecidable in general, one common workaround involves searching for invariants that guarantee non-termination. The existence of such invariants provides a definitive answer to the termination problem, whereas their absence is inconclusive. This strategy hence circumvents the undecidability barrier. In 17, we investigated the automatic synthesis of invariants expressible in Presburger arithmetic, which are suitable for systems relying solely on integer variables.
In 34, we introduced what we coined constraint loops, where the values of the variables in the next iteration of the loop are chosen non-deterministically, subject to satisfying a set of linear inequalities. This often arises due to abstractions when modeling a complex loop in a program. Termination in this context means that every possible non-deterministic choice eventually leads to loop termination. While our results are currently limited by the number of dimensions (i.e., the number of variables within the loop), they are already technically complex. This line of research is ongoing.
7.3 Verification and Analysis of Dynamic Properties of Biological Systems
Participants: Thomas Sturm.
Approximate Conservation Laws.
Section 3.3 presented an example of analyzing the kinetics of a chemical reaction network across multiple timescales 58. While the reduction method described is broadly applicable, it can fail in certain cases. A primary source of failure is the degeneracy of the quasi-steady state, which occurs when the fast dynamics exhibit a continuum of steady states. This situation typically arises when the truncated fast ODEs possess first integrals, i.e., quantities conserved along any trajectory but fixed to arbitrary values depending on the initial conditions. As a result, the quasi-steady states lose hyperbolicity, as the Jacobian matrix for the fast dynamics becomes singular. To address this limitation, we have introduced the concept of approximate conservation laws, enabling further reductions.
From a technical perspective, this framework necessitates parametric adaptations of several established algorithms in Symbolic Computation. One straightforward example is the computation of the rank of a matrix with real parameters, producing a formal finite case distinction where possible ranks are paired with necessary and sufficient conditions expressed as Tarski formulas. This approach helps identify critical cases related to the aforementioned singularity in the Jacobian. Another example involves the use of comprehensive Gröbner bases in parametric computations for certain syzygy modules. A key challenge in all such algorithms is the combinatorial explosion in the number of cases.
To mitigate this issue, we employ SMT solving and real quantifier elimination techniques to detect inconsistencies and prune the case distinction tree early. However, since these decision procedures are typically double-exponential in complexity, they can become bottlenecks, particularly when the degrees of polynomial terms increase, potentially preventing termination within a reasonable timeframe. As the results remain valid even without eliminating some redundant cases, we combine multiple methods and impose suitable timeouts. This work has culminated in two articles published in the SIAM Journal on Applied Dynamical Systems 14, 15.
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
Participants: Thomas Bagrel, Horatiu Cirstea, Marie Duflot-Kremer, Engel Lefaucheux, Stephan Merz, Mohamed Amine Snoussi.
TLA+ Trace Validation
-
Duration:
January 2023 – December 2024
-
Industrial Partner:
Oracle Corporation
-
Team participants:
Horatiu Cirstea, Stephan Merz
-
Summary:
The objective of this work is to find discrepancies between traces of distributed programs collected during their execution and high-level specifications, written in TLA+, of the algorithms that the programs are supposed to implement.
Type systems for the memory safety of functional programs
-
Duration:
April 2022 – March 2025
-
Industrial Partner:
Tweag
-
Team participants:
Thomas Bagrel, Horatiu Cirstea
-
Summary:
In his PhD work supported by a CIFRE contract, Thomas Bagrel studies type systems and corresponding constructions in a pure functional calculus with destinations at its core for guaranteeing programs that are memory safe and can be compiled to efficient machine code.
Reengineering protocols for industrial controllers
-
Duration:
May 2023 – April 2026
-
Industrial Partner:
Westinghouse France
-
Team participants:
Amine Snoussi, Marie Duflot-Kremer, Engel Lefaucheux, Stephan Merz
-
Summary:
In his PhD work supported by a CIFRE contract, Amine Snoussi aims at constructing formal models and simulations of protocols that are used for industrial controllers, in particular for the diagnosis and control of electronic components in nuclear power plants.
Event-B modeling for Human-Machine Interaction
-
Duration:
June 2024 – June 2025
-
Industrial Partner:
SAS H-AUGENPLUS
-
Team participants:
Dominique Méry
-
Summary:
The objective of this work is to assist in the development of Event-B models for HMI systems.
9 Partnerships and cooperations
9.1 International initiatives
9.1.1 Inria associate team
-
Title:
CAtalyzing progRess in smt solving and proof assistants via Modularity, proof trAnslation, and proof reconstruction (CARMA)
-
Duration:
2024 - 2026
-
Coordinators:
Sophie Tourret and Haniel Barbosa (hbarbosa@dcc.ufmg.br)
-
Partners:
Universidade Federal de Minas Gerais Belo Horizonte (Brésil)
-
Inria contact:
Sophie Tourret
-
Summary:
SMT solving is a technique for determining the satisfiability of formulas modulo background theories in first- and higher-order logic. SMT solvers are versatile tools with many applications. The Carma associate team aims at improving the state of the art in SMT solving on three fronts. Our first objective is to counter the research slowdown created by the tight interconnection of parts in state-of-the-art SMT solvers. We will do this by creating a new SMT solver to act as a vessel for research, with a strong emphasis on modularity. Our goal is that all components can simply be plugged in and out to make it easy to upgrade and serve as a platform for comparison between different techniques. The tentative name of this new solver is ModulariT. Our second objective concerns higher-order SMT and the missing components to make it competitive. We are convinced that one of the missing key components is an efficient conflict-based instantiation technique for higher-order logic. We plan to provide this component for ModulariT (that will be designed to operate on first- and higher-order logic from the start). Our third objective concerns the coexistence of various proof formats for SMT solving. We aim at more interoperability so that the various formats do not create a divide in the community. Specifically, our aim will be to provide a tool for translating Alethe proofs originating from TLA+ specifications (extracted from the proof assistant TLAPS) to Dedukti, a logical framework based on the -calculus modulo, in which many logics and theories can be expressed, that has become the lingua franca of proof translation.
This year, there were several exchanges between Belo Horizonte and Nancy. Haniel Barbosa visited for 2 weeks and took part in the SAT/SMT/AR summer school co-organized in Nancy by Sophie Tourret. A master student of Haniel Barbosa stayed for more than a month in Nancy to collaborate with VERIDIS members on the third objective and attend the SAT/SMT/AR summer school. Sophie Tourret went to Brazil for a week and this led to a new work direction: the integration of SMT-based abduction in a proof assistant.
9.1.2 Participation in other International Programs
AiRobo
Participants: Sorin Stratulat.
-
Title:
Artificial Intelligence based Robotics
-
Partner Institution(s):
- University of Macedonia, Greece
- RWTH, Germany
- Eszterhazy Karoly Catholic University, Hungary
- West University of Timisoara, Romania
-
Date/Duration:
December 2023 - November 2026
-
Additional info/keywords:
AiRobo 29 is an ERASMUS+ project that aims to increase the quality and the attractivity of related departments at the partner universities, by a significant raise of the level of competence and skills of the relevant academic staff in the field of Artificial Intelligence based Robotics. The correct functioning of such safety-critical systems is ensured by formal verifications using theorem provers such as Theorema and Coq, as well as SAT and SMT solvers such as SMT-RAT. Some sorting algorithms, similar to those used by robots in applications like parcel sorting and waste sorting, have been formally verified using Theorema and Coq in 30.
9.2 International research visitors
Alistair Finn Hackett.
-
Status
PhD student
-
Institution of origin:
University of British Columbia
-
Country:
Canada
-
Dates:
August 2024 - November 2024
-
Context of the visit:
Trace validation for distributed systems
-
Mobility program/type of mobility:
research stay
9.3 National initiatives
ANR Project BiSoUS
-
Title:
Better Synthesis for Underspecified Quantitative Systems
-
Duration:
March 2023 – February 2027
-
Coordinator:
Didier Lime, École Centrale de Nantes & LS2N
-
Partner Institutions:
- IRISA, Rennes
- LIPN, University Sorbonne Paris Nord (Paris 13)
- LS2N École Centrale de Nantes (coordinator)
- LMF, University Paris-Saclay
-
Team participants:
Marie Duflot-Kremer, Engel Lefaucheux
-
Summary:
Computer systems are ubiquitous and identifying their possible defects is crucial already at the earliest stages of their development, when many aspects, including the environments or the execution platforms, have not been fixed. Verification must then be performed on underspecified models and should give understandable answers. In this project, we aim at developing verification techniques for underspecified models that take this explainability constraint into account, by optimizing resources, such as energy or memory, and synthesizing more precise requirements on the underspecified aspects of the models under which the system behaves correctly. We depart from classical formalisms and consider their combined extensions with three complementary ingredients: costs/rewards for resource consumption; parameters for unknown quantitative characteristics; and games for representing all the behaviours of the underspecified system.
-
Keywords:
Verification, Model checking, parametrised systems, games with guarantees
- More information:
ANR Project BLaSST
-
Title:
Enhancing B Language Reasoners Using SAT and SMT Techniques
-
Duration:
March 2022 – February 2026
-
Coordinator:
Stephan Merz
-
Partner Institutions:
- Inria Nancy (coordinator)
- University of Artois & CRIL, Lens
- CLEARSY, Aix-en-Provence
- University of Liège, Belgium
-
Team participants:
Pascal Fontaine, Stephan Merz, Vincent Trélat, Sophie Tourret
-
Summary:
The BLaSST project targets bridging combinatorial and symbolic techniques in automatic theorem proving, in particular for proof obligations generated from B models. It focuses on advancing the state of the art in automated reasoning, in particular SAT and SMT techniques, and on making these techniques available to software verification. More specifically, encoding techniques, optimized resolution techniques, model generation, and lemma suggestion will be investigated. The expected scientific impact is a substantially higher degree of automation of solvers for expressive input languages by leveraging higher-order reasoning and enumerative instantiations over finite domains, as well as useful feedback for verification conditions that cannot be proved. The effectiveness of the techniques developed in the project will be quantified by applying them to benchmark sets provided by the industrial partner. The industrial impact of BLaSST will be a higher productivity of proof engineers. The collections of benchmarks and the reasoning engines will be made openly available under permissive open-source licenses.
-
Keywords:
B method, deductive verification, SAT, SMT, higher-order logic
- More information:
ANR Project DISCONT
-
Title:
Correct integration of discrete and continuous models
-
Duration:
March 2018 – December 2024
-
Coordinator:
Dominique Méry
-
Partner Institutions:
- University of Lorraine (coordinator)
- ENSEEIHT & IRIT, Toulouse
- University Paris Est & LACL, Créteil
- CLEARSY, Aix-en-Provence
-
Team participants:
Dominique Méry
-
Summary:
Cyber-Physical Systems (CPSs) connect the real world to software systems through a network of sensors and actuators that interact in complex ways, depending on context and involving different spatial and temporal scales. Typically, a discrete software controller interacts with its physical environment in a closed-loop schema where input from sensors is processed and output is generated and communicated to actuators. We are concerned with the verification of the correctness of such discrete controllers, which requires correct integration of discrete and continuous models. Correctness should arise from a design process based on sound abstractions and models of the relevant physical laws. The systems are generally characterized by differential equations with solutions in continuous domains; discretization steps are therefore of particular importance for assessing the correctness of CPSs. DISCONT aims at bridging the gap between the discrete and continuous worlds of formal methods and control theory. We will lift the level of abstraction above that found in current bridging techniques and provide associated methodologies and tools. Our concrete objectives are to develop a formal hybrid model, elaborate refinement steps for control requirements, propose a rational step-wise design method and support tools, and validate them based on use cases from a range of application domains.
-
Keywords:
cyber-physical systems, discrete models, continuous models, refinement, verification, tools
- More information:
ANR Project EBRP
-
Title:
Enhancing EventB and RODIN: EventB-Rodin-Plus
-
Duration:
January 2020 – December 2026
-
Coordinator:
Dominique Méry
-
Partner Institutions:
- INPT-ENSEEIHT & IRIT, Toulouse
- CentraleSupelec & LRI
- University of Lorraine & LORIA
- University Paris-Est Créteil & LACL
- University of Düsseldorf, Germany
- University of Southampton, School of Electronics and Computer Science, United Kingdom
-
Team participants:
Dominique Méry
-
Keywords:
formal IDE, theory, proof management, cyber-physical systems, discrete models, continuous models, refinement, verification, tools
-
Summary:
The purpose of EBRP is to enhance Event-B and the corresponding Rodin toolset. This will be done by engaging in some basic research dealing with various mathematical theories that are not currently available in Event-B and Rodin. The development of complex systems usually involves different scientific disciplines and skills. For instance, modeling behaviors and interactions of autonomous systems may require concepts from control theory such as differential equations, communication protocols, resource allocation, access control rules, etc. EBRP targets the definition of extension mechanisms for Event-B rather than defining domain-specific modeling languages, and implementing those mechanisms within Rodin.
- More information:
ANR Project ICSPA
-
Title:
Interoperable and Confident Set-based Proof Assistants
-
Duration:
January 2022 – December 2026
-
Coordinator:
Catherine Dubois, ENSIIE & Samovar
-
Partner Institutions:
- ENSIIE & Samovar, Évry
- Inria (Nancy and Saclay research centers)
- University Paul Sabatier & IRIT, Toulouse
- University of Montpellier & LIRMM, Montpellier
- CLEARSY, Aix-en-Provence
-
Team participants:
Alessio Coltellacci, Dominique Méry, Stephan Merz
-
Summary:
The B, Event-B, and TLA+ formal methods are based on different flavors of set theory. The ICSPA project aims at formally relating these different theories for allowing users (i) to independently certify proofs carried out using the automatic proof tools developed for these formal methods and (ii) to transfer developments, including their proofs, carried out in one of these languages to another one. The objectives are to reinforce confidence in developments carried out using these methods and to enable interoperability between them. The foundation for achieving these goals lies in the encoding of the set theories in the Dedukti logical framework developed at Inria Saclay, which implements the -calculus modulo.
-
Keywords:
B method, TLA+, set theory, logical framework
- More information:
10 Dissemination
10.1 Promoting scientific activities
10.1.1 Scientific events: organization
General chair, scientific chair
- Dominique Méry was a scientific co-chair of ICFEM 2024 (Hiroshima,Japan).
- Stephan Merz was a scientific co-chair of IJCAR 2024 (Nancy) France, a co-organizer of the ETAPS Mentoring Workshop (Luxembourg), and a co-chair of the TLA+ Community Meeting (Milan, Italy).
- Sorin Stratulat was the co-chair of the 5th International Workshop on Automated (Co)inductive Theorem Proving (WAIT2024), co-located with IJCAR 2024 (Nancy, France).
- Sophie Tourret was a scientific co-chair of the SAT/SMT/AR summer school 2024 (Nancy, France).
Member of organizing committees
- Sophie Tourret was the workshop chair of IJCAR 2024, Nancy, France.
10.1.2 Scientific events: selection
Chair of conference program committees
- Julie Cailler was the PC chair of the 11th Workshop on Horn Clauses for Verification and Synthesis (HCVS2024, Luxembourg) and Web chair of the 24th Conference in Formal Methods in Computer-Aided Design (FMCAD 2024, Prague, Czech Republic).
Member of conference program committees
- Horatiu Cirstea : RuleML 2024.
- Dominique Méry : ABZ 2024, FMAS 2024, ICECCS 2024, STAF 2024, TASE 2024.
- Stephan Merz : ABZ 2024, FMICS 2024, ICFEM 2024, IJCAR 2024, SEFM 2024.
- Thomas Sturm : CASC 2024 (and workshop: SC-Square 2024)
- Sophie Tourret : IJCAI 2024, IJCAR 2024 (and workshops: LFMTP 2024, PAAR 2024).
- Uwe Waldmann : IJCAR 2024.
- Christoph Weidenbach : IJCAR 2024.
Reviewer
- Julie Cailler : IJCAR 2024, FM 2024, CPP 2024, VMCAI 2024, FMCAD 2024.
10.1.3 Journal
Editor-in-chief
- Thomas Sturm : Mathematics in Computer Science, Springer
Member of editorial boards
- Dominique Méry : Science of Computer Programming, Formal Aspects of Computing.
- Thomas Sturm : Journal of Symbolic Computation, Elsevier
- Christoph Weidenbach : Journal of Automated Reasoning, Springer
Reviewer - reviewing activities
- Stephan Merz : Science of Computer Programming, Software and System Modeling.
- Sophie Tourret : Journal of Artificial Intelligence Research, Science of Computer Programming, Journal of Symbolic Computation, Journal of Automated Reasoning.
- Martin Vassor : International Journal on Software and Systems Modeling.
- Uwe Waldmann : Journal of Logical and Algebraic Methods in Programming.
10.1.4 Invited talks
- Julie Cailler : “SC-TPTP : Extending the TPTP Format for Sequent-based Proofs” at the national days of the research groups LVP (GDR GPL) and Scalp (GDR IFM), Paris, France.
- Julie Cailler : Interviews and experience-sharing at the annual meeting of GDR GPL, Strasbourg, France.
- Thomas Sturm : “A Subtropical Approach to Positive Solutions of Large Polynomials”, BIRS Workshop 24w5197, Granada, Spain.
- Sophie Tourret : “The hows and whys of higher-order SMT” at the SMT workshop 2024, Montréal, Canada.
- Uwe Waldmann : “The Saturation Framework” at the annual meeting of the IFIP working group 1.6, Nancy, France.
10.1.5 Leadership within the scientific community
- Dominique Méry : IFIP Working Group 1.3 on Foundations of System Specification.
-
Stephan Merz
:
- IFIP Working Group 2.2 on Formal Description of Programming Concepts,
- chairman of the TLA+ Specification Language Committee and member of the Governing Board of the TLA+ Foundation.
-
Thomas Sturm
:
- SC-Square steering committee member, invited in 2023,
- advisory positions in the EPRSC Projects EP/T015748/1 and EP/T015713/1, UK.
-
Sophie Tourret
:
- SAT/SMT/AR coordination committee member, invited in 2024,
- EuroProofNet european COST action core member, deputy leader of working group 2 on automated theorem provers, invited in 2024,
- CADE trustee, elected in 2022,
- PAAR steering committee member, invited in 2020.
-
Uwe Waldmann
:
- Ex-officio CADE trustee,
- Co-speaker of the Special Interest Group on Deduction Systems of the AI Chapter of the German Society of Informatics.
10.1.6 Research administration
- Julie Cailler : editor of the AAR newsletter.
-
Marie Duflot-Kremer
:
- member of the hiring committee for an assistant professor at Inspé, Université de Lorraine
- member of the hiring committee for an assistant professor at Université Sorbonne Paris Nord
-
Stephan Merz
:
- member of the board of the project committee of Inria Center at University of Lorraine;
- coach for ERC candidates at Inria (since May 2024).
-
Sophie Tourret
:
- Inria center at University of Lorraine, hiring committee for junior researchers;
- Univ. Lorraine, hiring committees for associate professor positions at Mines Nancy and Polytech;
- ComiDocs Loria: committee for hiring non-permanent scientists;
- ComiPers Inria Nancy: committee for hiring non-permanent scientists.
-
Uwe Waldmann
:
- scientific representative of MPI-INF within the CPT-section of the Max Planck Society;
- member of the 2025 CIS tenure-track selection committee of the Max Planck Society.
- ombudsperson of MPI-INF.
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- Licence: Julie Cailler , Programming 2, 20 HETD, L1 Universität Regensburg, Germany.
- Licence: Julie Cailler , Algorithms and imperative programming, 44 HETD, L1 Université de Lorraine, France.
- Licence: Julie Cailler , Propositionnel and first-order logic, 30 HETD, L2-L3 Université de Lorraine, France.
- Master: Julie Cailler , Software engineering, 20 HETD, 2A ENSEM, France.
- Master: Horatiu Cirstea , Programming paradigms, 32 HETD, M2 Informatique, Université de Lorraine, France.
- Master: Horatiu Cirstea , Software analysis and design, 80 HETD, M1 informatique, Université de Lorraine, France.
- Master: Horatiu Cirstea , Software engineering, 50 HETD, 2A ENSEM, Université de Lorraine, France.
- Licence: Horatiu Cirstea , Algorithms and complexity 3, 36 HETD, L2, Université de Lorraine, France.
- Licence: Marie Duflot-Kremer , Algorithms and programming 1, 100 HETD, L1, Université de Lorraine, France.
- Licence : Marie Duflot-Kremer , data bases, 10 HETD, L3, Université de Lorraine, France
- Licence : Marie Duflot-Kremer , Scientific Outreach, 30h ETD, L1, Université de Lorraine, France.
- Master: Marie Duflot-Kremer , Using unplugged activities to pass on computer science concepts to students, 38 HETD, master for future teachers, Université de Lorraine, France
- Master: Marie Duflot-Kremer , Elements of model checking, 18 HETD, M2 Informatique, Université de Lorraine, France.
- Master: Marie Duflot-Kremer , Distributed algorithms, 15 HETD, M1 Informatique, Université de Lorraine, France.
- Master: Marie Duflot-Kremer and Engel Lefaucheux, supervision of 2 students in a short "initiation à la recherche" internship, M1, Université de Lorraine
- Classe préparatoire universitaire: Engel Lefaucheux , Colles Langages et automates, 5 HETD, Université de Lorraine.
- Licence: Engel Lefaucheux , Algorithms and programming 2, 20 HETD, L2, Université de Lorraine.
- Classe préparatoire des INP: Engel Lefaucheux , Langages et Automates, 34.5 HETD, Université de Lorraine
- Master: Dominique Méry , Formal Modeling for Software-based Systems 40 HETD, M2 Informatique, Université de Lorraine, France.
- Master: Dominique Méry , Models and algorithms, M1 Telecom Nancy, 48 HETD, Université de Lorraine, France.
- Master: Dominique Méry , Formal Modeling for Software-based Systems, M2 Telecom Nancy, 24 HETD, Université de Lorraine, France.
- Master: Stephan Merz , Elements of model checking, 12 HETD, M2 Informatique, Université de Lorraine, France.
- Master: Stephan Merz , Distributed algorithms, 15 HETD, M1 Informatique, Université de Lorraine, France.
- Master: Stephan Merz , Secure Coding, M1 Mines Nancy, 13 HETD, Université de Lorraine, France.
- Master: Sorin Stratulat , Software design, 30 HETD, M2 Informatique, Université de Lorraine, France.
- Licence: Sorin Stratulat , Algorithms and programming, 105 HETD, L1 Informatique, Université de Lorraine, France.
- Licence: Sorin Stratulat , Logic for computer science, 26 HETD, L1 Informatique, Université de Lorraine, France.
- Master: Thomas Sturm , Decision Procedures for Specific Theories (Seminar), Universität des Saarlandes, Germany.
- Master: Sophie Tourret , Secure Coding, M1 Mines Nancy, 13 HETD, Université de Lorraine, France.
- Master: Martin Vassor , Python for engineers, 42 HETD, 2A and 3A, Mines Nancy, Université de Lorraine, France.
- Master: Uwe Waldmann , Automated Reasoning, 60 HETD, Universität des Saarlandes, Germany.
- Master: Uwe Waldmann , Automated Reasoning II, 40 HETD, Universität des Saarlandes, Germany.
- Master: Christoph Weidenbach , Automated Reasoning, 60 HETD, Universität des Saarlandes, Germany.
10.2.2 Supervision
- PhD in progress: Thomas Bagrel , Type systems for memory safety in functional programming languages, Université de Lorraine (CIFRE with Tweag company). Supervised by Horatiu Cirstea , since April 2022.
- PhD in progress: Ghilain Bergeron , Generating distributed programs from formal specifications, University of Lorraine. Supervised by Horatiu Cirstea and Stephan Merz , since October 2023.
- PhD in progress: Alessio Coltellacci , Formalizing TLA+ set theory and certifying proofs, University of Lorraine. Supervised by Gilles Dowek (Inria Saclay) and Stephan Merz , since January 2023.
- PhD in progress: Sarah Depernet , Verifying timed cybersecurity properties using formal methods, University of Lorraine. Supervised by Engel Lefaucheux and Stephan Merz .
- PhD in progress: Martin Desharnais , Verification in Isabelle/HOL of automated reasoning results, MPI for Informatics, Saarland University. Supervised by Jasmin Blanchette , Sophie Tourret and Christoph Weidenbach , since August 2021, submitted December 2024.
- PhD in progress: Hendrik Leidinger , SCL in First-Order Logic with Equality, Saarland University. Supervised by Christoph Weidenbach , since August 2020, submitted December 2024.
- PhD in progress: Lorenz Leutgeb , Reasoning with SCL, Saarland University. Supervised by Christoph Weidenbach , since October 2021.
- PhD in progress: Simon Schwarz , Automatic Reasoning for Security, Saarland University. Supervised by Christoph Weidenbach , since October 2022.
- PhD in progress: Amine Snoussi , Formal Reengineering of Communication Protocols for Controllers. University of Lorraine (CIFRE with Westinghouse France). Supervised by Marie Duflot-Kremer and Stephan Merz , since May 2023.
- PhD in progress: Vincent Trélat , Higher-Order SMT Solving for Proof Obligations in Set Theory. University of Lorraine. Supervised by Stephan Merz and Sophie Tourret , since October 2023.
10.2.3 Juries
- Stephan Merz reviewed the PhD theses of Gianluca Redondi (University of Trento, Italy) and of Srinidhi Nagendra (University Paris Cité, France).
- Marie Duflot-Kremer is a member of the board of the "CAPES NSI" jury (national competitive exam to hire secondary school teachers)
10.3 Popularization
10.3.1 Specific official responsibilities in science outreach structures
- Marie Duflot-Kremer is the deputy vice-president for outreach activities in the supervisory council of SIF (Société Informatique de France) and a member of the scientific committee of Fondation Blaise Pascal, which supports projects on popularization activities.
- Marie Duflot-Kremer is a member of the Interstices editorial board, a Web site launched by Inria that publishes popularization articles.
- Christoph Weidenbach is the head of the steering committee of the German Computer Science Competition for High School Students (BWINF) and a co-organizer and the president of the jury of the final round that took place in Munich in September 2024. Thomas Sturm was a member of that jury.
10.3.2 Participation in live events
- Marie Duflot-Kremer was co-organizer and director of a one week seminar “Les Cigognes” for girls in secondary school to help them discover research in mathematics and computer science in October 2024.
- Marie Duflot-Kremer organized a stand at the “Fête de la science” event (October 2023), to present unplugged computer science activities to the general public with the help of bachelor students.
- Marie Duflot-Kremer set up a stand at different scientific events, "semaine des mathématiques" (Nancy), "matinées filles maths et sciences" (Nancy), "Festival Double Science" (Paris), "évènement autour des sciences du numérique" (Blainville sur l'Eau), "Journées du matrimoine" (Jarville la Malgrange), "festival du jeu vidéo" (Jarville la Malgrange)
- Marie Duflot-Kremer gave a conference talk to secondary school teachers and students, and a two-hours workshop for teachers on unplugged computer science activities in Châlons en Champagne.
- Marie Duflot-Kremer took part in ten 1-hour meetings with secondary school students to present computer science and research, mostly within the Chiche program.
- Marie Duflot-Kremer co-organised the EMI school on science outreach, aiming at dicovering, creating and testing unplugged computer science outreach activities.
- Marie Duflot-Kremer was the referent researcher of a group of secondary school kids doing research for the MathenJEANS programme.
- Sophie Tourret : participant at the EMI school on science outreach, including half a day of live outreach toward middle school and high school students.
11 Scientific production
11.1 Major publications
- 1 inproceedingsveriT: an open, trustable and efficient SMT-solver.Proc. Conference on Automated Deduction (CADE)5663Lecture Notes in Computer ScienceMontreal, CanadaSpringer2009, 151-156back to text
- 2 articleA complete and terminating approach to linear integer solving.Journal of Symbolic Computation100September 2020, 102-136HALDOIback to text
- 3 incollectionThe Event-B Modelling Method - Concepts and Case Studies.Logics of Specification LanguagesMonographs in Theoretical Computer ScienceSpringerFebruary 2008, 33-140HALback to text
- 4 inproceedingsTLA+ Proofs.18th International Symposium On Formal Methods - FM 20127436Lecture Notes in Computer ScienceParis, FranceSpringer2012, 147-154back to text
- 5 articleRedlog: Computer algebra meets computer logic.ACM SIGSAM Bull.3121997, 2-9back to text
- 6 articleDetection of Hopf bifurcations in chemical reaction networks using convex coordinates.Journal of Computational Physics291March 2015, 279 - 302HALDOI
- 7 bookTemporal Logic and State Systems.Texts in Theoretical Computer ScienceSpringer2008, 436URL: http://hal.inria.fr/inria-00274806/en/
- 8 articleSuperposition Decides the First-Order Logic Fragment Over Ground Theories.Mathematics in Computer Science642012, 427-456
- 9 incollectionThe Specification Language TLA+.Logics of specification languagesMonographs in Theoretical Computer ScienceSpringer2008, 401-452HALback to text
- 10 inproceedingsVerification and synthesis using real quantifier elimination.Proc. ISSAC 2011San Jose, United StatesACM PressJune 2011, 329HALDOI
- 11 inproceedingsSPASS Version 3.5.22nd International Conference on Automated Deduction (CADE-22)5663LNAIMontreal, CanadaSpringer2009, 140-145back to text
11.2 Publications of the year
International journals
Invited conferences
International peer-reviewed conferences
National peer-reviewed Conferences
Conferences without proceedings
Edition (books, proceedings, special issue of a journal)
Reports & preprints
11.3 Cited publications
- 48 bookModeling in Event-B: System and Software Engineering.Cambridge University Press2010back to text
- 49 inproceedingsParametric real-time reasoning.Proc. 25th Annual ACM Symp. Theory of ComputingSan Diego, CA, USAACM1993, 592-601back to text
- 50 articleRewrite-Based Equational Theorem Proving with Selection and Simplification.Journal of Logic and Computation431994, 217-247back to text
- 51 bookRefinement calculus---A systematic introduction.Springer Verlag1998back to text
- 52 incollectionSatisfiability Modulo Theories.Handbook of Satisfiability185Frontiers in Artificial Intelligence and ApplicationsIOS PressFebruary 2009, 26825-885back to text
- 53 articleA tale of two diagnoses in probabilistic systems.Information and Computation2692019, 104441back to text
- 54 inproceedingsA Datalog Hammer for Supervisor Verification Conditions Modulo Simple Linear Arithmetic.13th Intl. Symp. Frontiers of Combining Systems (FroCoS 2021)12941Lecture Notes in Computer ScienceSpringer2021, 3-24back to text
- 55 inproceedingsDeciding the Bernays-Schoenfinkel Fragment over Bounded Difference Constraints by Simple Clause Learning over Theories.22nd Intl. Conf. Verification, Model Checking, and Abstract Interpretation (VMCAI 2021)12597Lecture Notes in Computer ScienceSpringer2021, 511-533back to text
- 56 inproceedingsThe Dark Side of Timed Opacity.Advances in Information Security and Assurance2009, 21--30back to text
- 57 inproceedingsSMT solvers for Rodin.ABZ - Third International Conference on Abstract State Machines, Alloy, B, VDM, and Z - 20127316Lecture Notes in Computer SciencePisa, ItalySpringer2012, 194-207back to text
- 58 articleAlgorithmic Reduction of Biological Networks with Multiple Time Scales.Mathematics in Computer Science153September 2021, 499 - 534HALDOIback to textback to text
- 59 bookSpecifying Systems.Boston, Mass.Addison-Wesley2002back to text
- 60 articleBioModels Database: A Free, Centralized Database of Curated, Published, Quantitative Kinetic Models of Biochemical and Cellular Systems.Nucleic acids res.34suppl_1January 2006, D689-D691DOIback to text
- 61 articleTransmission Dynamics and Control Strategies Assessment of Avian Influenza A (H5N6) in the Philippines.Infectious Disease Modelling32018, 35-59DOIback to text
- 62 bookProgramming from Specifications.2nd editionPrentice Hall1998back to text

