Keywords
Computer Science and Digital Science
- A5.5.1. Geometrical modeling
- A5.10.1. Design
- A7.1. Algorithms
- A8.1. Discrete mathematics, combinatorics
- A8.3. Geometry, Topology
- A8.4. Computer Algebra
Other Research Topics and Application Domains
- B1.1.1. Structural biology
- B1.2.3. Computational neurosciences
- B2.6. Biological and medical imaging
- B3.3. Geosciences
- B5.5. Materials
- B5.6. Robotic systems
- B5.7. 3D printing
- B6.2.2. Radio technology
1 Team members, visitors, external collaborators
Research Scientists
- Olivier Devillers [Team leader, INRIA, Senior Researcher, HDR]
- Sylvain Lazard [INRIA, Senior Researcher, HDR]
- Guillaume Moroz [INRIA, Researcher]
- Marc Pouget [INRIA, Researcher, HDR]
- Monique Teillaud [INRIA, Senior Researcher, HDR]
Faculty Members
- Vincent Despre [UL, Associate Professor]
- Laurent Dupont [UL, Associate Professor]
- Xavier Goaoc [UL, Professor, HDR]
- Alba Marina Malaga Sabogal [UL, Associate Professor]
Post-Doctoral Fellow
- Florent Koechlin [INRIA, from Feb 2022]
PhD Students
- Loîc Dubois [ENS de Lyon, from Mar 2022]
- Charles Duménil [UL, until May 2022]
- Matthias Fresacher [UL, until Apr 2022]
- Nuwan Herath Mudiyanselage [UL, ATER, from Sep 2022]
- Nuwan Herath Mudiyanselage [INRIA, until Aug 2022]
- Camille Lanuel [UL, from Oct 2022]
- Léo Valque [UL]
Technical Staff
- Rémi Imbach [UL, Engineer, from May 2022]
Interns and Apprentices
- Léo Kulinski [D1, Intern, from Mar 2022 until Jun 2022]
Administrative Assistant
- Isabelle Blanchard [INRIA]
Visiting Scientist
- Justin Dallant [UNIV LIBRE BRUXELLES, from Nov 2022]
External Collaborator
- Valentin Feray [CNRS, from Nov 2022, HDR]
2 Overall objectives
Starting in the eighties, the emerging computational geometry community has put a lot of effort into designing and analyzing algorithms for geometric problems. The most commonly used framework was to study the worst-case theoretical complexity of geometric problems involving linear objects (points, lines, polyhedra...) in Euclidean spaces. This so-called classical computational geometry has some known limitations:
- Objects: dealing with objects only defined by linear equations.
- Ambient space: considering only Euclidean spaces.
- Complexity: worst-case complexities often do not capture realistic behaviour.
- Dimension: complexities are often exponential in the dimension.
- Robustness: ignoring degeneracies and rounding errors.
Even if these limitations have already got some attention from the community 42, a quick look at the proceedings of the flagship conference SoCG1 shows that these topics still need a big effort.
It should be stressed that, in this document, the notion of certified algorithms is to be understood with respect to robustness issues. In other words, certification does not refer to programs that are proven correct with the help of mechanical proof assistants such as Coq, but to algorithms that are proven correct on paper even in the presence of degeneracies and computer-induced numerical rounding errors.
We address several of the above limitations:
Non-linear computational geometry. Curved objects are ubiquitous in the world we live in. However, despite this ubiquity and decades of research in several communities, curved objects are far from being robustly and efficiently manipulated by geometric algorithms. Our work on, for instance, quadric intersections and certified drawing of plane curves has proven that dramatic improvements can be accomplished when the right mathematics and computer science concepts are put into motion. In this direction, many problems are fundamental and solutions have potential industrial impact in Computer Aided Design and Robotics for instance. Intersecting NURBS (Non-uniform rational basis splines) and meshing singular surfaces in a certified manner are important examples of such problems.
Non-Euclidean computational geometry. Triangulations are central geometric data structures in many areas of science and engineering. Traditionally, their study has been limited to the Euclidean setting. Needs for triangulations in non-Euclidean settings have emerged in many areas dealing with objects whose sizes range from the nuclear to the astrophysical scale, and both in academia and in industry. It has become timely to extend the traditional focus on of computational geometry and encompass non-Euclidean spaces.
Probability in computational geometry. The design of efficient algorithms is driven by the analysis of their complexity. Traditionally, worst-case input and sometimes uniform distributions are considered and many results in these settings have had a great influence on the domain. Nowadays, it is necessary to be more subtle and to prove new results in between these two extreme settings. For instance, smoothed analysis, which was introduced for the simplex algorithm and which we applied successfully to convex hulls, proves that such promising alternatives exist.
Discrete geometric structures. Many geometric algorithms work, explicitly or implicitly, over discrete structures such as graphs, hypergraphs, lattices that are induced by the geometric input data. For example, convex hulls or straight-line graph drawing are essentially based on orientation predicates, and therefore operate on the so-called order type of the input point set. Order types are a subclass of oriented matroids that remains poorly understood: for instance, we do not even know how to sample this space with reasonable bias. One of our goals is to contribute to the development of these foundations by better understanding these discrete geometric structures.
3 Research program
3.1 Non-linear computational geometry

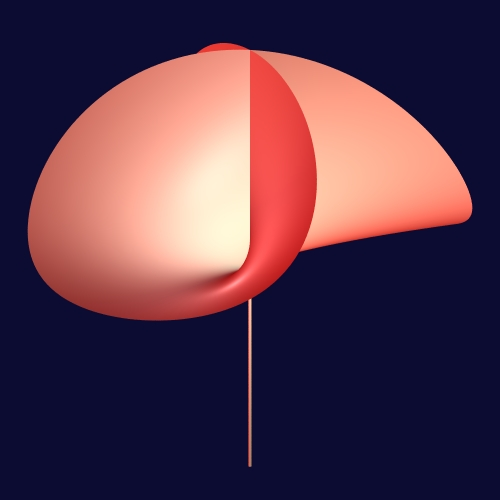
As mentioned above, curved objects are ubiquitous in real world problems and in computer science and, despite this fact, there are very few problems on curved objects that admit robust and efficient algorithmic solutions without first discretizing the curved objects into meshes. Meshing curved objects induces a loss of accuracy which is sometimes not an issue but which can also be most problematic depending on the application. In addition, discretization induces a combinatorial explosion which could cause a loss in efficiency compared to a direct solution on the curved objects (as our work on quadrics has demonstrated with flying colors 49, 50, 48, 52, 58). But it is also crucial to know that even the process of computing meshes that approximate curved objects is far from being resolved. As a matter of fact there is no algorithm capable of computing in practice meshes with certified topology of even rather simple singular (that is auto-intersecting) 3D surfaces, due to the high constants in the theoretical complexity and the difficulty of handling degenerate cases. Part of the difficulty comes from the unintuitive fact that the structure of an algebraic object can be quite complicated, as depicted in the Whitney umbrella (see Figure 1), the surface with equation whose origin (the “special” point of the surface) is a vertex of the arrangement induced by the surface while the singular locus is simply the whole -axis. Even in 2D, meshing an algebraic curve with the correct topology, that is in other words producing a correct drawing of the curve (without knowing where the domain of interest is), is a very difficult problem on which we have recently made important contributions 35, 36, 57.
Thus producing practical, robust, and efficient algorithmic solutions to geometric problems on curved objects is a challenge on all and even the most basic problems. The basicness and fundamentality of the two problems we mentioned above on the intersection of 3D quadrics and on the drawing in a topologically certified way of plane algebraic curves show rather well that the domain is still in its infancy. And it should be stressed that these two sets of results were not anecdotal but flagship results produced during the lifetime of the Vegas team (the team preceding Gamble).
There are many problems in this theme that are expected to have high long-term impacts. Intersecting NURBS (Non-uniform rational basis splines) in a certified way is an important problem in computer-aided design and manufacturing. As hinted above, meshing objects in a certified way is important when topology matters. The 2D case, that is essentially drawing plane curves with the correct topology, is a fundamental problem with far-reaching applications in research or R&D. Notice that on such elementary problems it is often difficult to predict the reach of the applications; as an example, we were astonished by the scope of the applications of our software on 3D quadric intersection2 which was used by researchers in, for instance, photochemistry, computer vision, statistics and mathematics.
3.2 Non-Euclidean computational geometry
Triangulations, in particular Delaunay triangulations, in the Euclidean space have been extensively studied throughout the 20th century and they are still a very active research topic. Their mathematical properties are now well understood, many algorithms to construct them have been proposed and analyzed (see the book of Aurenhammer et al.29). Some members of Gamble have been contributing to these algorithmic advances (see, e.g. 34, 68, 47, 33); they have also contributed robust and efficient triangulation packages through the state-of-the-art Computational Geometry Algorithms Library Cgal whose impact extends far beyond computational geometry. Application fields include particle physics, fluid dynamics, shape matching, image processing, geometry processing, computer graphics, computer vision, shape reconstruction, mesh generation, virtual worlds, geophysics, and medical imaging.3
It is fair to say that little has been done on non-Euclidean spaces, in spite of the large number of questions raised by application domains. Needs for simulations or modeling in a variety of domains4 ranging from the infinitely small (nuclear matter, nano-structures, biological data) to the infinitely large (astrophysics) have led us to consider 3D periodic Delaunay triangulations, which can be seen as Delaunay triangulations of the 3D flat torus, i.e., the quotient of under the action of some group of translations 40. This work has already yielded a fruitful collaboration with astrophysicists 53, 69 and new collaborations with physicists are emerging. To the best of our knowledge, our Cgal package 39 is the only publicly available software that computes Delaunay triangulations of a 3D flat torus, in the special case where the domain is cubic. This case, although restrictive, is already useful.5 We have also generalized this algorithm to the case of general -dimensional compact flat manifolds 41. As far as non-compact manifolds are concerned, past approaches, limited to the two-dimensional case, have stayed theoretical 60.
Interestingly, even for the simple case of triangulations on the sphere, the software packages that are currently available are far from offering satisfactory solutions in terms of robustness and efficiency 38.
Moreover, while our solution for computing triangulations in hyperbolic spaces can be considered as ultimate 31, the case of hyperbolic manifolds has hardly been explored. Hyperbolic manifolds are quotients of a hyperbolic space by some group of hyperbolic isometries. Their triangulations can be seen as hyperbolic periodic triangulations. Periodic hyperbolic triangulations and meshes appear for instance in geometric modeling 64, neuromathematics 43, or physics 65. Even the case of the Bolza surface (a surface of genus 2, whose fundamental domain is the regular octagon in the hyperbolic plane) shows mathematical difficulties 32, 55.
3.3 Probability in computational geometry
In most computational geometry papers, algorithms are analyzed in the worst-case setting. This often yields too pessimistic complexities that arise only in pathological situations that are unlikely to occur in practice. On the other hand, probabilistic geometry provides analyses with great precision 62, 63, 37, but using hypotheses with much more randomness than in most realistic situations. We are developing new algorithmic designs improving state-of-the-art performance in random settings that are not overly simplified and that can thus reflect many realistic situations.
Sixteen years ago, smooth analysis was introduced by Spielman and Teng analyzing the simplex algorithm by averaging on some noise on the data 67 (and they won the Gödel prize). In essence, this analysis smoothes the complexity around worst-case situations, thus avoiding pathological scenarios but without considering unrealistic randomness. In that sense, this method makes a bridge between full randomness and worst case situations by tuning the noise intensity. The analysis of computational geometry algorithms within this framework is still embryonic. To illustrate the difficulty of the problem, we started working in 2009 on the smooth analysis of the size of the convex hull of a point set, arguably the simplest computational geometry data structure; then, only one very rough result from 2004 existed 44 and we only obtained in 2015 breakthrough results, but still not definitive 46, 45, 51.
Another example of a problem of different flavor concerns Delaunay triangulations, which are rather ubiquitous in computational geometry. When Delaunay triangulations are computed for reconstructing meshes from point clouds coming from 3D scanners, the worst-case scenario is, again, too pessimistic and the full randomness hypothesis is clearly not adapted. Some results exist for “good samplings of generic surfaces” 28 but the big result that everybody wishes for is an analysis for random samples (without the extra assumptions hidden in the “good” sampling) of possibly non-generic surfaces.
Trade-offs between full randomness and worst case may also appear in other forms such as dependent distributions, or random distributions conditioned to be in some special configurations. In particular, simulating geometric distributions with repulsive properties, such as the determinantal point process, is currently out of reach for more than a few hundred points 54. Yet it has practical applications in physics to simulate particules with repulsion such as electrons 59, to simulate the distribution of network antennas 30, or in machine learning 56.
3.4 Discrete geometric structures
Our work on discrete geometric structures develops in several directions, each one probing a different type of structure. Although these objects appear unrelated at first sight, they can be tackled by the same set of probabilistic and topological tools.
A first research topic is the study of Order types. Order types are combinatorial encodings of finite (planar) point sets, recording for each triple of points the orientation (clockwise or counterclockwise) of the triangle they form. This already determines properties such as convex hulls or half-space depths, and the behaviour of algorithms based on orientation predicates. These properties for all (infinitely many) -point sets can be studied through the finitely many order types of size . Yet, this finite space is poorly understood: its estimated size leaves an exponential margin of error, no method is known to sample it without concentrating on a vanishingly small corner, the effect of pattern exclusion or VC dimension-type restrictions are unknown. These are all directions we actively investigate.
A second research topic is the study of Embedded graphs and simplicial complexes. Many topological structures can be effectively discretized, for instance combinatorial maps record homotopy classes of embedded graphs and simplicial complexes represent a large class of topological spaces. This raises many structural and algorithmic questions on these discrete structures; for example, given a closed walk in an embedded graph, can we find a cycle of the graph homotopic to that walk? (The complexity status of that problem is unknown.) Going in the other direction, some purely discrete structures can be given an associated topological space that reveals some of their properties (e.g. the Nerve theorem for intersection patterns). An open problem is for instance to obtain fractional Helly theorems for set systems of bounded topological complexity.
Another research topic is that of Sparse inclusion-exclusion formulas. For any family of sets , by the principle of inclusion-exclusion we have
where is the indicator function of . This formula is universal (it applies to any family of sets) but its number of summands grows exponentially with the number of sets. When the sets are balls, the formula remains true if the summation is restricted to the regular triangulation; we proved that similar simplifications are possible whenever the Venn diagram of the is sparse. There is much room for improvements, both for general set systems and for specific geometric settings. Another interesting problem is to combine these simplifications with the inclusion-exclusion algorithms developed, for instance, for graph coloring.
4 Application domains
Many domains of science can benefit from the results developed by Gamble. Curves and surfaces are ubiquitous in all sciences to understand and interpret raw data as well as experimental results. Still, the non-linear problems we address are rather basic and fundamental, and it is often difficult to predict the impact of solutions in that area. The short-term industrial impact is likely to be small because, on basic problems, industries have used ad hoc solutions for decades and have thus got used to it.
The example of our work on quadric intersection is typical: even though we were fully convinced that intersecting 3D quadrics is such an elementary/fundamental problem that it ought to be useful, we were the first to be astonished by the scope of the applications of our software 6 (which was the first and still is the only one —to our knowledge— to compute robustly and efficiently the intersection of 3D quadrics) which has been used by researchers in, for instance, photochemistry, computer vision, statistics, and mathematics. Our work on certified drawing of plane (algebraic) curves falls in the same category. It seems obvious that it is widely useful to be able to draw curves correctly (recall also that part of the problem is to determine where to look in the plane) but it is quite hard to come up with specific examples of fields where this is relevant. A contrario, we know that certified meshing is critical in mechanical-design applications in robotics, which is a non-obvious application field. There, the singularities of a manipulator often have degrees higher than 10 and meshing the singular locus in a certified way is currently out of reach. As a result, researchers in robotics can only build physical prototypes for validating, or not, the approximate solutions given by non-certified numerical algorithms.
The fact that several of our pieces of software for computing non-Euclidean triangulations had already been requested by users long before they become public in Cgal is a good sign for their wide future impact. This will not come as a surprise, since most of the questions that we have been studying followed from discussions with researchers outside computer science and pure mathematics. Such researchers are either users of our algorithms and software, or we meet them in workshops. Let us only mention a few names here. Rien van de Weijgaert 53, 69 (astrophysicist, Groningen, NL) and Michael Schindler 66 (theoretical physicist, ENSPCI, CNRS, France) used our software for 3D periodic weighted triangulations. Stephen Hyde and Vanessa Robins (applied mathematics and physics at Australian National University) used our package for 3D periodic meshing. Olivier Faugeras (neuromathematics, INRIA Sophia Antipolis) had come to us and mentioned his needs for good meshes of the Bolza surface 43 before we started to study them. Such contacts are very important both to get feedback about our research and to help us choose problems that are relevant for applications. These problems are at the same time challenging from the mathematical and algorithmic points of view. Note that our research and our software are generic, i.e., we are studying fundamental geometric questions, which do not depend on any specific application. This recipe has made the sucess of the Cgal library.
Probabilistic models for geometric data are widely used to model various situations ranging from cell phone distribution to quantum mechanics. The impact of our work on probabilistic distributions is twofold. On the one hand, our studies of properties of geometric objects built on such distributions will yield a better understanding of the above phenomena and has potential impact in many scientific domains. On the other hand, our work on simulations of probabilistic distributions will be used by other teams, more maths oriented, to study these distributions.
5 Highlights of the year
The poisonous atmosphere maintained by the management of Inria towards the researchers creates an unhealthy climate not favourable to the "serene and efficient research" that is advocated by the COP.
6 New software and platforms
6.1 New software
6.1.1 earoots
-
Name:
Ehrlich-Aberth Roots
-
Keywords:
Root, Complex number, Univariate polynomial
-
Functional Description:
It uses Ehrlich-Aberth method to find polynomial complex roots in double precision. The code has been written to benefit from auto-vectorization.
-
News of the Year:
This software is used by the hefroots software and is integrated in the commercial software Maple 2023.
- URL:
-
Contact:
Guillaume Moroz
-
Participant:
Guillaume Moroz
6.1.2 hefroots
-
Name:
Hyperbolic, Elliptic and Flat ROOT Solver
-
Keywords:
Polynomial equations, Complex number
-
Scientific Description:
This software for solving polynomial equations is based on a recent result which consists in approximating a polynomial of large degree by a piecewise polynomial function on the complex plane.
-
Functional Description:
This software takes as input a file containing the coefficients of a univariate polynomial and returns the list of its complex roots.
-
News of the Year:
Integration work has been done for Maplesoft's commercial computer algebra software. Hefroots will be used to find the complex roots of a polynomial in Maple 2023.
- URL:
- Publication:
-
Authors:
Guillaume Moroz, Rémi Imbach
-
Contact:
Guillaume Moroz
6.1.3 FCA2V
-
Name:
Fast Certified Algebraic Variety Visualization
-
Keywords:
Algebraic curve, Discrete Cosine Transform
-
Functional Description:
FCA2V computes a drawing of high resolution of a plane curve defined by a bivariate polynomial equation. It uses a non-uniform grid based on the Chebyshev nodes to take advantage of multipoint evaluation techniques via the Discrete Cosine Transform.
- URL:
- Publication:
-
Author:
Nuwan Herath Mudiyanselage
-
Contact:
Nuwan Herath Mudiyanselage
7 New results
7.1 Non-Linear Computational Geometry
Participants: Laurent Dupont, Nuwan Herath Mudiyanselage, Sylvain Lazard, Guillaume Moroz, Marc Pouget.
7.1.1 Fast High-Resolution Drawing of Algebraic Curves
We address the problem of computing a drawing of high resolution of a plane curve defined by a bivariate polynomial equation . Given a grid of fixed resolution, a drawing is a subset of pixels. Our goal is to compute an approximate drawing that (i) contains all the parts of the curve that intersect the pixel edges, (ii) excludes a pixel when the evaluation of with interval arithmetic on each of its four edges is far from zero.
One of the challenges for computing drawings on a high-resolution grid is to minimize the complexity due to the evaluation of the input polynomial. Most state-of-the-art approaches focus on bounding the number of independent evaluations. Using state-of-the-art Computer Algebra techniques, we design new algorithms that amortize the evaluations and improve the complexity for computing such drawings.
Our main contribution is to use a non-uniform grid based on the Chebyshev nodes to take advantage of multipoint evaluation techniques via the Discrete Cosine Transform. We propose two new algorithms that compute drawings and compare them experimentally on several classes of high degree polynomials. Notably, one of those approaches is faster than state-of-the-art drawing software. 18.
7.1.2 New data structure for univariate polynomial approximation and applications to root isolation, numerical multipoint evaluation, and other problems
We present a new data structure to approximate accurately and efficiently a polynomial of degree given as a list of coefficients . Its properties allow us to improve the state-of-the-art bounds on the bit complexity for the problems of root isolation and approximate multipoint evaluation. This data structure also leads to a new geometric criterion to detect ill-conditioned polynomials, implying notably that the standard condition number of the zeros of a polynomial is at least exponential in the number of roots of modulus less than or greater than 2.
Given a polynomial of degree with for , isolating all its complex roots or evaluating it at points can be done with a quasi-linear number of arithmetic operations. However, considering the bit complexity, the state-of-the-art algorithms require at least bit operations even for well-conditioned polynomials and when the accuracy required is low. Given a positive integer , we can compute our new data structure and evaluate at points in the unit disk with an absolute error less than in bit operations, where means that we omit logarithmic factors. We also show that if is the absolute condition number of the zeros of , then we can isolate all the roots of in bit operations. Moreover, our algorithms are simple to implement. For approximating the complex roots of a polynomial, we implemented a small prototype in Python/NumPy that is an order of magnitude faster than the state-of-the-art solver MPSolve for high degree polynomials with random coefficients. This result was presented in 2022 at the FOCS 2021 conference 20.
7.2 Non-Euclidean Computational Geometry
Participants: Vincent Despré, Loïc Dubois, Benedikt Kolbe, Alba Marina Málaga Sabogal, Monique Teillaud.
7.2.1 Computing a Dirichlet domain for a hyperbolic surface
The goal of this paper is to exhibit and analyze an algorithm that takes a given closed orientable hyperbolic surface and outputs an explicit Dirichlet domain. The input is a fundamental polygon with side pairings. While grounded in topological considerations, the algorithm makes key use of the geometry of the surface. We introduce data structures that reflect this interplay between geometry and topology and show that the algorithm finishes in polynomial time, in terms of the initial perimeter length and the genus of the surface 27.
In collaboration with Benedikt Kolbe (now at University of Bonn) and Hugo Parlier (University of Luxembourg).
7.3 Probabilistic Analysis of Geometric Data Structures and Algorithms
Participants: Olivier Devillers, Charles Duménil.
7.3.1 Expected Size of the 3-Dimensional Delaunay Triangulation of Random Points on a Surface
We proved that the size of the Delaunay triangulation of set of points drawn on a surface with a random distribution is linear. The Delaunay triangulation, is a geometrical object that appeared recurrently in the scientific history. In dimension 2, the Delaunay triangulation is the set of triangles for which the circumscribing circle does not contain other points of . This definition is generalizable in higher dimensions. Today, the Delaunay triangulation is one the most studied structures in computational geometry. For the 2 dimensional case, we know that the size of the Delaunay triangulation remains linear in terms of the number of points. In 3 dimension, it is not anymore the case. The size of the 3D-Delaunay triangulation can range from linear to quadratic. This size depends on how the points are distributed in . On a surface, the size of the Delaunay triangulation will depend both on the surface and on how they are distributed on this surface. To model points, we choose to use a Poisson point process since it verifies properties of homogeneity and independence that are convenient for the computations. In order to prove the expected bound for the uniform sample distributed on a cylinder, Devillers et al. remarked that the intersection of the cylinder with a sphere passing though two points and on the cylinder always contains a specific triangle drawn on the cylinder. That leads them to study a 2-dimensional graph in which two points are neighbors if there exists such a triangle that does not contain other data points. Such a graph has expected size , and this is how they obtain the bound. Thus, we define a kind of empty region graphs, we formalize a method to compute lower and upper bounds on their expected size, and give tight results for such graphs. As Attali et al. pointed out, the intersection of a sphere with a generic surface has almost an elliptic shape, aligned with the curvature directions of the surface. This leads us to study a particular empty region graph for which the regions are axis-aligned ellipses. We prove, that if the involved ellipses have an aspect ratio ranging from to 1, with , then the expected number of neighbors of any point in the graph is . We use these results on empty-region graph to treat the case of the oblate spheroid first and prove that the Delaunay triangulation has linear size in this case. Then we extend these results to any generic surface since at the first order, any surface behave locally as a spheroid 22.
7.4 Discrete Geometric structures
Participants: Xavier Goaoc.
7.4.1 Convex Hulls of Random Order Types
We establish the following two main results on order types of points in general position in the plane (realizable simple planar order types, realizable uniform acyclic oriented matroids of rank 3):
-
(a)
The number of extreme points in an -point order type, chosen uniformly at random from all such order types, is on average . For labeled order types, this number has average and variance at most 3.
-
(b)
The (labeled) order types read off a set of points sampled independently from the uniform measure on a convex planar domain, smooth or polygonal, or from a Gaussian distribution are concentrated, i.e. such sampling typically encounters only a vanishingly small fraction of all order types of the given size.
Result (a) generalizes to arbitrary dimension d for labeled order types with the average number of extreme points and constant variance. We also discuss to what extent our methods generalize to the abstract setting of uniform acyclic oriented matroids. Moreover, our methods allow to show the following relative of the Erdős-Szekeres theorem: for any fixed , as , a proportion of the -point simple order types contain a triangle enclosing a convex -chain over an edge. For the unlabeled case in (a), we prove that for any antipodal, finite subset of the 2-dimensional sphere, the group of orientation preserving bijections is cyclic, dihedral or one of , or (and each case is possible). These are the finite subgroups of and our proof follows the lines of their characterization by Felix Klein.
15. In collaboration with Emo Welzl (ETH Zürich)
7.4.2 The Topology of the set of line Transversals
We prove that for any set of pairwise disjoint open convex set in , the connected components of the set of lines intersecting every member of are contractible. The same result holds for directed lines. 25.
In collaboration with Otfried Cheong and Andreas Holmsen (KAIST)
7.4.3 No weak epsilon nets for lines and convex sets in space
We prove that there exist no weak -nets of constant size for lines and convex sets in . 24.
In collaboration with Otfried Cheong and Andreas Holmsen (KAIST)
7.5 Miscellaneous
Participant: Florent Koechlin.
7.5.1 New Analytic Techniques for Proving the Inherent Ambiguity of Context-Free Languages.
This article extends the work of Flajolet on the relation between generating series and inherent ambiguity. We first propose an analytic criterion to prove the infinite inherent ambiguity of some context-free languages, and apply it to give a purely combinatorial proof of the infinite ambiguity of Shamir’s language. Then we show how Ginsburg and Ullian’s criterion on unambiguous bounded languages translates into a useful criterion on generating series, which generalises and simplifies the proof of the recent criterion of Makarov. We then propose a new criterion based on generating series to prove the inherent ambiguity of languages with interlacing patterns, like or with . We illustrate the applicability of these two criteria on many examples 19.
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
8.1.1 Waterloo Maple Inc.
Participants: Laurent Dupont, Sylvain Lazard, Guillaume Moroz, Marc Pouget, Rémi Imbach.
Company: Waterloo Maple Inc.
Duration: 2 years, renewable
Participants: Gamble and Ouragan Inria teams
Abstract: A renewable two-years licence and cooperation agreement was signed on April 1st, 2018 between Waterloo Maple Inc., Ontario, Canada (represented by Laurent Bernardin, its Executive Vice President Products and Solutions) and Inria. On the Inria side, this contract involves the teams Gamble and Ouragan (Paris), and it is coordinated by Fabrice Rouillier (Ouragan).
F. Rouillier and Gamble are the developers of the Isotop software for the computation of topology of curves. The transfer of a version of Isotop to Waterloo Maple Inc. should be done on the long run.
This contract was amended last year to include the new software hefroots for the isolation of the complex roots of a univariate polynomial. The transfer of hefroots to Waterloo Maple Inc. started at the end of 2021 with the help of the independent contractor Rémi Imbach. Rémi Imbach was then hired for one year by Inria through the ADT program and hefroots will be included in Maple 2023.
8.1.2 GeometryFactory
Participants: Monique Teillaud.
Company: GeometryFactory
Duration: permanent
Participants: Inria and GeometryFactory
Abstract: Cgal packages developed in Gamble are commercialized by GeometryFactory.
9 Partnerships and cooperations
9.1 International initiatives
9.1.1 Inria associate team not involved in an Inria International Lab or an international program
FIP
Participants: Xavier Goaoc, Florent Koechlin.
-
Title:
Finite point sets and Intersection Patterns
-
Duration:
Jan 2021 -> Dec 2023
-
Coordinator:
Andreas Holmsen (andreash@kaist.edu)
-
Partners:
- Korea Advanced Institute of Science and Technology Daejeon (Corée du Sud)
-
Inria contact:
Xavier Goaoc
-
Summary:
This project tackles two families of problems in discrete and computational geometry, dealing respectively with finite point sets and to intersection patterns of geometric set systems. The two PI already collaborate on one family of problems and have worked independently on the other. The goal of the associate team is to broaden this two-person collaboration, and help the emergence of new research groups.
- Project website:
9.1.2 ANR PRCI
ANR SoS
Participants: Vincent Despré, Loïc Dubois, Camille Lanuel, Alba Malaga, Monique Teillaud.
-
Title:
Structures on Surfaces
-
Duration:
4 years + 1 year Covid'19 extension
-
Starting date:
April 1st, 2018
-
Coordinator:
Monique Teillaud
-
Partners:
- Gamble project-team, Inria.
- LIGM (Laboratoire d'Informatique Gaspard Monge), Université Gustave Eiffel. Local Coordinator: Éric Colin de Verdière.
- RMATH (Mathematics Research Unit), University of Luxembourg. National Coordinator: Hugo Parlier.
-
Inria contact:
Monique Teillaud
-
Summary:
SoS is co-funded by ANR (ANR-17-CE40-0033) and FNR (INTER/ANR/16/11554412/SoS) as a PRCI (Projet de Recherche Collaborative Internationale).
The central theme of this project is the study of geometric and combinatorial structures related to surfaces and their moduli. Even though they work on common themes, there is a real gap between communities working in geometric topology and computational geometry and SoS aims to create a long-lasting bridge between them. Beyond a common interest, techniques from both ends are relevant and the potential gain in perspective from long-term collaborations is truly thrilling.
In particular, SoS aims to extend the scope of computational geometry, a field at the interface between mathematics and computer science that develops algorithms for geometric problems, to a variety of unexplored contexts. During the last two decades, research in computational geometry has gained wide impact through CGAL, the Computational Geometry Algorithms Library. In parallel, the needs for non-Euclidean geometries are arising, e.g., in geometric modeling, neuromathematics, or physics. Our goal is to develop computational geometry for some of these non-Euclidean spaces and make these developments readily available for users in academia and industry.
To reach this aim, SoS follows an interdisciplinary approach, gathering researchers whose expertise cover a large range of mathematics, algorithms and software. A mathematical study of the objects considered is performed, together with the design of algorithms when applicable. Algorithms are analyzed both in theory and in practice after prototype implementations, which are improved whenever it makes sense to target longer-term integration into CGAL.
Our main objects of study are Delaunay triangulations and circle patterns on surfaces, polyhedral geometry, and systems of disjoint curves and graphs on surfaces.
- Project website:
Other international visits to the team
Boris Bukh
-
Status
professor
-
Institution of origin:
Carneggie Mellon University
-
Country:
USA
-
Dates:
July 3-12
-
Context of the visit:
Collaboration with X. Goaoc
-
Mobility program/type of mobility:
research stay
Justin Dallant
-
Status
PhD student
-
Institution of origin:
Université Libre de Bruxelles
-
Country:
Belgique
-
Dates:
September 20-22, and November 15h-December 16th
-
Context of the visit:
Collaboration with X. Goaoc and F. Koechlin
-
Mobility program/type of mobility:
research stay (Bourse de mobilité de doctorants et de post doctorants (BE>FR) pour les anciens lauréats PHC TOURNESOL)
9.1.3 Visits to international teams
Research stays abroad
- X. Goaoc and F. Koechlin visited the group of A. Holsmen in KAIST (South Korea) for 3 and 4 weeks, respectively.
9.2 National initiatives
9.2.1 ANR PRC
ANR Aspag
Participants: Olivier Devillers, Charles Duménil, Xavier Goaoc, Sylvain Lazard, Guillaume Moroz, Ji Won Park, Marc Pouget.
-
Title:
Analyse et Simulation Probabilistes d'Algorithmes Géométriques
-
Duration:
4 years + 1 year Covid'19 extension
-
Starting date:
January 1st, 2018
-
Coordinator:
Olivier Devillers
-
Partners:
- Gamble project-team, Inria.
- Labri (Laboratoire Bordelais de Recherche en Informatique), Université de Bordeaux. Local Coordinator: Philippe Duchon.
- Laboratoire de Mathématiques Raphaël Salem, Université de Rouen. Local Coordinator: Pierre Calka.
- LAMA (Laboratoire d'Analyse et de Mathématiques Appliquées), Université Paris-Est Marne-la-Vallée. Local Coordinator: Matthieu Fradelizi
-
Inria contact:
Olivier Devillers
-
Summary:
The ASPAG projet is funded by ANR under number ANR-17-CE40-0017 .
The analysis and processing of geometric data has become routine in a variety of human activities ranging from computer-aided design in manufacturing to the tracking of animal trajectories in ecology or geographic information systems in GPS navigation devices. Geometric algorithms and probabilistic geometric models are crucial to the treatment of all this geometric data, yet the current available knowledge is in various ways much too limited: many models are far from matching real data, and the analyses are not always relevant in practical contexts. One of the reasons for this state of affairs is that the breadth of expertise required is spread among different scientific communities (computational geometry, analysis of algorithms and stochastic geometry) that historically had very little interaction. The Aspag project brings together experts of these communities to address the problem of geometric data. We will more specifically work on the following three interdependent directions.
(1) Dependent point sets: One of the main issues of most models is the core assumption that the data points are independent and follow the same underlying distribution. Although this may be relevant in some contexts, the independence assumption is too strong for many applications.
(2) Simulation of geometric structures: The phenomena studied in (1) involve intricate random geometric structures subject to new models or constraints. A natural first step would be to build up our understanding and identify plausible conjectures through simulation. Perhaps surprisingly, the tools for an effective simulation of such complex geometric systems still need to be developed.
(3) Understanding geometric algorithms: the analysis of algorithms is an essential step in assessing the strengths and weaknesses of algorithmic principles, and is crucial to guide the choices made when designing a complex data processing pipeline. Any analysis must strike a balance between realism and tractability; the current analyses of many geometric algorithms are notoriously unrealistic. Aside from the purely scientific objectives, one of the main goals of Aspag is to bring the communities closer in the long term. As a consequence, the funding of the project is crucial to ensure that the members of the consortium will be able to interact on a very regular basis, a necessary condition for significant progress on the above challenges.
- Project website:
ANR MinMax
Participant: Xavier Goaoc.
-
Title:
MIN-MAX
-
Duration:
4 years
-
Starting date:
January 1st, 2019
-
Coordinator:
Stéphane Sabourau (Université Paris-Est Créteil)
-
Partners:
- Université Paris Est Créteil, Laboratoire d'Analyse et de Mathématiques Appliquées (LAMA). Local coordinator: Stéphane Sabourau
- Université de Tours, Institut Denis Poisson. Local coordinator: Laurent Mazet. This node includes two participants from Nancy, Benoît Daniel (IECL) and Xavier Goaoc (Loria, Gamble).
-
Inria contact:
Xavier Goaoc
-
Summary:
The MinMax projet is funded by ANR under number ANR-19-CE40-0014
This collaborative research project aims to bring together researchers from various areas – namely, geometry and topology, minimal surface theory and geometric analysis, and computational geometry and algorithms – to work on a precise theme around min-max constructions and waist estimates.
- Project website:
10 Dissemination
Participants: Vincent Despré, Olivier Devillers, Laurent Dupont, Alba Malaga, Sylvain Lazard, Guillaume Moroz, Marc Pouget, Monique Teillaud.
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
General chair, scientific chair
Monique Teillaud coordinated the organization of the workshop Structures on Surfaces (CIRM, Marseille, May 2-6), which gathered more than 60 participants.
Seminar
David Eppstein (University of California, Irvine, USA) was invited to give a talk in the framework of the (virtual) SoS seminar.
10.1.2 Scientific events: selection
Chair of conference program committees
Xavier Goaoc was co-chair of SoCG'2022, the flagship conference of compuational geometry.
Member of the conference program committees
Monique Teillaud was a member of the program committee of EuroCG, the 38th European Workshop of Computational Geometry (Perugia, Italy, March 14-16). She was also a member of the committee for the Young Researchers Forum of CGWeek, the Computational Geometry Week (Berlin, Germany, June 7–10).
Reviewer
All members of the team are regular reviewers for the conferences of our field, namely Symposium on Computational Geometry (SoCG), European Symposium on Algorithms (ESA), Symposium on Discrete Algorithms (SODA), International Symposium on Symbolic and Algebraic Computation (ISSAC), etc.
10.1.3 Journal
Member of the editorial boards
Monique Teillaud is a managing editor of JoCG, Journal of Computational Geometry.
Reviewer - reviewing activities
All members of the team are regular reviewers for the journals of our field, namely Discrete and Computational Geometry (DCG), Journal of Computational Geometry (JoCG), International Journal on Computational Geometry and Applications (IJCGA), Journal on Symbolic Computations (JSC), SIAM Journal on Computing (SICOMP), Mathematics in Computer Science (MCS), etc.
10.1.4 Software Project
Member of the Editorial Boards
Marc Pouget and Monique Teillaud are members of the CGAL editorial board.
10.1.5 Invited talks
Monique Teillaud was invited to give a (virtual) talk at the NYC Geometry Seminar “Flipping Geometric Triangulations on Hyperbolic Surfaces”.
10.1.6 Research administration
Team members are involved in various committees managing the scientific life of the lab or at a national level.
Local
- INRIA Comission Information et Édition Scientifique (L.Dupont),
- Fédération Charles Hermite (X. Goaoc),
- INRIA Comité de centre (X. Goaoc),
- LORIA Conseil scientifique (S. Lazard),
- LORIA department chair (S. Lazard),
- UL Prof hiring committee (chair, S. Lazard),
- Two identical UL and Sorbonne Paris Nord Univ. associate Prof hiring committees (chair, S. Lazard) in the context of an exchange of positions,
- INRIA hiring commitee (X. Goaoc),
- INRIA PhD and postdoc hiring committee (chair, S. Lazard),
- École doctorale IAEM (S. Lazard),
- INRIA Comité des utilisateurs des moyens informatiques (chair, G. Moroz),
- INRIA Commission de développement technologique (G. Moroz),
- CLHSCT (G. Moroz),
- Agos (M. Pouget),
- LORIA Conseil de laboratoire (M. Teillaud),
- Co-organization of “Tutotechno” (M. Teillaud).
National
- INRIA Mission Jeunes Chercheurs (chair, S. Lazard).
10.2 Teaching - Supervision - Juries
10.2.1 Teaching Committees
- V. Despré: Head of the Engineer diploma speciality SIR, Systèmes d'Information et Réseaux, Polytech Nancy, Université de Lorraine.
- L. Dupont is the secretary of Commission Pédagogique Nationale Carrières Sociales / Information-Communication / Métiers du Multimédia et de l'Internet (2017-2022).
- L. Dupont represents the Commission Pédagogique Nationale Carrières Sociales / Information-Communication / Métiers du Multimédia et de l'Internet at the national working group on D.U.T/B.U.T reform
- L. Dupont: Head of the Bachelor diploma Licence Professionnelle Animateur, Facilitateur de Tiers-lieux Eco-Responsables, Université de Lorraine,
- L. Dupont: Responsible of fablab "Charlylab" of I.U.T. Nancy-Charlemagne,
- X. Goaoc is the chair of the computer science department of l'École des Mine
- X. Goaoc is a member of the Conseil d'administration de l'École des Mine
10.2.2 Teaching
- Master: V. Despré, Algorithmique distribuée, 48h, M1, Polytech Nancy, France.
- Master: O. Devillers & X. Goaoc, Modèles d'environnements, planification de trajectoires, 18h, M2 AVR, Université de Lorraine, France (web).
- Licence: L. Dupont, Web development, 45h, L1, Université de Lorraine, France.
- Licence: L. Dupont, Web development, 150h, L2, Université de Lorraine, France.
- Licence: L. Dupont Web development and Social networks 70h L3, Université de Lorraine, France.
- Licence: L. Dupont, 3D printing and CAO 40h, L3, Université de Lorraine, France.
- Licence : X. Goaoc, Algorithms and complexity, 57 HETD, L3, École des Mines de Nancy, France.
- Master: X. Goaoc, Computer architecture, 32 HETD, M1, École des Mines de Nancy Nancy, France.
- Master: X. Goaoc, Introduction to blockchains, 52 HETD, M1, École des Mines de Nancy + Polytech Nancy, France.
- Licence: A. Málaga, Information systems and databases, 86h, L1, Université de Lorraine, France.
- Licence: A. Málaga, Content Management Systems, 40h, L1, Université de Lorraine, France.
- Master: M. Pouget, Introduction to computational geometry, 10.5h, M2, École Nationale Supérieure de Géologie, France.
- Licence : G. Moroz, Programmation et structures de données, 20 HETD, L3, École des Mines de Nancy, France.
10.2.3 Supervision
- PhD: Charles Duménil, Expected Size of the 3-Dimensional Delaunay Triangulation of Random Points on a Surface, defended may 2022, supervised by Olivier Devillers.
- PhD in progress: Loïc Dubois, Untangling graphs on surfaces, started in Oct. 2021, supervised by Vincent Despré and Éric Colin de Verdière (Marne la Vallée).
- PhD in progress: Nuwan Herath, Fast algorithm for the visualization of surfaces, started in Nov. 2019, supervised by Sylvain Lazard, Guillaume Moroz and Marc Pouget.
- PhD in progress: Camille Lanuel, A toolbox for hyperbolic surfaces, started in Oct. 2021, supervised by Vincent Despré and Monique Teillaud.
- PhD in progress: Léo Valque, Rounding 3D meshes, started in Sept. 2020, supervised by Sylvain Lazard.
- Master internship M2: Léo Kulinski, Meshing singular surfaces, Mars - June 2022, MPRI, supervised by Gquillaume Moroz and Marc Pouget.
10.2.4 Juries
- X. Goaoc was on the reading and defense committees of the Habilitation à diriger les recherches d'Arnaud de Mesmay.
- S. Lazard was on the PhD defense committee (chair) of Matthieu Zins.
10.3 Popularization
- O. Devillers presented research carreer in several different classes in highschool within the Chiche program.
- G. Moroz is a member of the Mathematics Olympiads committee of the Nancy-Metz academy.
- L. Dupont presented mixed reality software for autistic people in collaboration with the association J. B. Thiery.
- A. Malaga gave a presentation "polyhedra" in primary school in Thionville within the program « Regards de géomètres
- A. Malaga, L. Valque, L. Kulinski, and F. Koechlin animated a booth at the "salon de Culture et Jeux mathématiques"
11 Scientific production
11.1 Major publications
- 1 inproceedingsImproved Routing on the Delaunay Triangulation.ESA 2018 - 26th Annual European Symposium on AlgorithmsHelsinki, Finland2018
- 3 inproceedingsFlipping Geometric Triangulations on Hyperbolic Surfaces.SoCG 2020 - 36th International Symposium on Computational GeometryZurich, Switzerland2020
- 4 articleRounding meshes in 3D.Discrete and Computational GeometryApril 2020
- 5 articleShellability is NP-complete.Journal of the ACM (JACM)6632019
- 6 inproceedingsConvex Hulls of Random Order Types.SoCG 2020 - 36th International Symposium on Computational Geometry16436th International Symposium on Computational Geometry (SoCG 2020)Best paper awardZürich / Virtual, Switzerland2020, 49:1--49:15
- 7 articleReliable Location with Respect to the Projection of a Smooth Space Curve.Reliable Computing262018, 13-55
- 8 inproceedingsImplementing Delaunay Triangulations of the Bolza Surface.33rd International Symposium on Computational Geometry (SoCG 2017)Brisbane, AustraliaJuly 2017, 44:1--44:15
- 9 articleWorkspace, Joint space and Singularities of a family of Delta-Like Robot.Mechanism and Machine Theory127September 2018, 73-95
- 10 articleBivariate triangular decompositions in the presence of asymptotes.Journal of Symbolic Computation822017, 123--133
11.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Doctoral dissertations and habilitation theses
Reports & preprints
11.3 Cited publications
- 28 inproceedingsComplexity of the Delaunay triangulation of points on surfaces: the smooth case.Proceedings of the 19th Annual Symposium on Computational Geometry2003, 201--210URL: http://dl.acm.org/citation.cfm?id=777823
- 29 bookVoronoi diagrams and Delaunay triangulations.World Scientific2013, URL: http://www.worldscientific.com/worldscibooks/10.1142/8685
- 30 articleOn a few statistical applications of determinantal point processes.ESAIM: Procs602017, 180-202URL: https://doi.org/10.1051/proc/201760180
- 31 articleHyperbolic Delaunay complexes and Voronoi diagrams made practical.Journal of Computational Geometry52014, 56--85
- 32 inproceedingsDelaunay triangulations on orientable surfaces of low genus.Proceedings of the 32nd International Symposium on Computational Geometry2016, 20:1--20:15
- 33 inproceedingsIncremental construction of the Delaunay graph in medium dimension.Proceedings of the 25th Annual Symposium on Computational Geometry2009, 208--216
- 34 articleApplications of random sampling to on-line algorithms in computational geometry.Discrete and Computational Geometry81992, 51--71
- 35 techreportImproved algorithms for solving bivariate systems via Rational Univariate Representations.INRIAFebruary 2015
- 36 articleSeparating linear forms and Rational Univariate Representations of bivariate systems.Journal of Symbolic Computation68May 2015, 84-119
- 37 phdthesisTessellations, convex hulls and Boolean model: some properties and connections.Université René Descartes - Paris V2009
- 38 inproceedingsRobust and Efficient Delaunay Triangulations of Points on or Close to a Sphere.Proceedings of the 9th International Symposium on Experimental Algorithms6049Lecture Notes in Computer Science2010, 462--473
- 39 incollection3D Periodic Triangulations.CGAL User and Reference Manual3.5CGAL Editorial Board2009, URL: http://doc.cgal.org/latest/Manual/packages.html#PkgPeriodic3Triangulation3Summary
- 40 inproceedingsComputing 3D Periodic Triangulations.Proceedings of the 17th European Symposium on Algorithms5757Lecture Notes in Computer Science2009, 59--70
-
41
inproceedingsDelaunay Triangulations of Point Sets in Closed Euclidean
-Manifolds.Proceedings of the 27th Annual Symposium on Computational Geometry2011, 274--282 - 42 incollectionApplication challenges to computational geometry: CG impact task force report.Advances in Discrete and Computational Geometry223Contemporary MathematicsProvidenceAmerican Mathematical Society1999, 407--463
- 43 articleBifurcation of hyperbolic planforms.Journal of Nonlinear Science212011, 465--498URL: http://link.springer.com/article/10.1007/s00332-010-9089-3
- 44 inproceedingsExtreme points under random noise.Proceedings of the 12th European Symposium on Algorithms2004, 264--274URL: http://dx.doi.org/10.1007/978-3-540-30140-0_25
- 45 inproceedingsComplexity analysis of random geometric structures made simpler.Proceedings of the 29th Annual Symposium on Computational GeometryJune 2013, 167-175
- 46 inproceedingsOn the smoothed complexity of convex hulls.Proceedings of the 31st International Symposium on Computational GeometryLipics2015
- 47 articleThe Delaunay hierarchy.International Journal of Foundations of Computer Science132002, 163-180
- 48 articleNear-Optimal Parameterization of the Intersection of Quadrics: III. Parameterizing Singular Intersections.Journal of Symbolic Computation4332008, 216--232
- 49 articleNear-optimal parameterization of the intersection of quadrics: I. The generic algorithm.Journal of Symbolic Computation4332008, 168--191
- 50 articleNear-optimal parameterization of the intersection of quadrics: II. A classification of pencils.Journal of Symbolic Computation4332008, 192--215
- 51 articleSilhouette of a random polytope.Journal of Computational Geometry712016, 14
- 52 articleA complete, exact and efficient implementation for computing the edge-adjacency graph of an arrangement of quadrics.Journal of Symbolic Computation4642011, 467-494
- 53 inproceedingsVideo: the sticky geometry of the cosmic web.Proceedings of the 28th Annual Symposium on Computational Geometry2012, 421--422
- 54 articleDeterminantal processes and independence.Probab. Surv.32006, 206-229
- 55 inproceedingsImplementing Delaunay triangulations of the Bolza surface.Proceedings of the Thirty-third International Symposium on Computational Geometry2017, 44:1--44:15
- 56 articleDeterminantal Point Processes for Machine Learning.Foundations and Trends® in Machine Learning52–32012, 123-286URL: http://dx.doi.org/10.1561/2200000044
- 57 techreportBivariate triangular decompositions in the presence of ssymptotes.INRIASeptember 2015
- 58 articleIntersecting quadrics: an efficient and exact implementation.Computational Geometry: Theory and Applications351-22006, 74--99
- 59 articleThe coincidence approach to stochastic point processes.Advances in Applied Probability711975, 83–122
- 60 articleVoronoi diagrams on orbifolds.Computational Geometry: Therory and Applications81997, 219--230
- 61 miscPeriodic meshes for the CGAL library.Research NoteLondres, United Kingdom2014
-
62
articleÜber die konvexe Hülle von
zufällig gerwähten Punkten I.Z. Wahrsch. Verw. Gebiete21963, 75--84URL: http://dx.doi.org/10.1007/BF00535300 -
63
articleÜber die konvexe Hülle von
zufällig gerwähten Punkten II.Z. Wahrsch. Verw. Gebiete31964, 138--147URL: http://dx.doi.org/10.1007/BF00535973 - 64 inproceedingsHyperbolic centroidal Voronoi tessellation.Proceedings of the ACM Symposium on Solid and Physical Modeling2010, 117--126URL: http://dx.doi.org/10.1145/1839778.1839795
- 65 articleTuning the fragility of a glassforming liquid by curving space.Physical Review Letters1012008, 155701(1)--155701(4)URL: http://dx.doi.org/10.1103/PhysRevLett.101.155701
- 66 articleCavity averages for hard spheres in the presence of polydispersity and incomplete data.The European Physical Journal E2015, 38--97URL: http://dx.doi.org/10.1103/PhysRevE.88.022315
- 67 articleSmoothed analysis: why the simplex algorithm usually takes polynomial time.Journal of the ACM5132004, 385--463URL: http://dx.doi.org/10.1145/990308.990310
- 68 bookTowards dynamic randomized algorithms in computational geometry.758Lecture Notes Comput. Sci.Springer-Verlag1993, URL: http://www.springer.com/gp/book/9783540575030
- 69 inproceedings Alpha, Betti and the megaparsec universe: on the homology and topology of the cosmic web. Transactions on Computational Science XIV 6970Lecture Notes in Computer ScienceSpringer-Verlag 2011, 60--101URL: http://dx.doi.org/10.1007/978-3-642-25249-5_3

