Keywords
Computer Science and Digital Science
- A2.3. Embedded and cyber-physical systems
- A3.1. Data
- A3.3. Data and knowledge analysis
- A3.4. Machine learning and statistics
- A5.1. Human-Computer Interaction
- A5.6. Virtual reality, augmented reality
- A5.10. Robotics
- A5.11. Smart spaces
- A6. Modeling, simulation and control
- A6.1. Methods in mathematical modeling
- A6.2. Scientific computing, Numerical Analysis & Optimization
- A6.3. Computation-data interaction
- A6.4. Automatic control
- A6.5. Mathematical modeling for physical sciences
- A8.4. Computer Algebra
- A8.11. Game Theory
- A9.2. Machine learning
- A9.3. Signal analysis
- A9.5. Robotics
- A9.7. AI algorithmics
- A9.9. Distributed AI, Multi-agent
- A9.10. Hybrid approaches for AI
Other Research Topics and Application Domains
- B2.1. Well being
- B2.5. Handicap and personal assistances
- B2.7. Medical devices
- B2.8. Sports, performance, motor skills
- B3.1. Sustainable development
- B3.5. Agronomy
- B5.2. Design and manufacturing
- B5.6. Robotic systems
- B5.7. 3D printing
- B8.1. Smart building/home
- B8.4. Security and personal assistance
- B9.1. Education
- B9.2. Art
- B9.9. Ethics
1 Team members, visitors, external collaborators
Research Scientists
- Jean-Pierre Merlet [Team leader, INRIA, Senior Researcher, HDR]
- Pierre Berthet-Rayne [CARANX MEDICAL, Industrial member, from Oct 2022]
- Yves Papegay [INRIA, Researcher, HDR]
- Odile Pourtallier [INRIA, Researcher]
- Eric Wajnberg [INRAE, Senior Researcher, HDR]
PhD Students
- Romain Tissot [INRIA]
- Alexandre Tran [INRIA, CIFRE]
Administrative Assistant
- Jane Desplanques [INRIA]
External Collaborator
- Eric Sejor [CHU NICE]
2 Overall objectives
HEPHAISTOS has been created as a team on January 1st, 2013 and as a project team in 2015.
The goal of the project is to set up a generic methodology for the design and evaluation of an adaptable and interactive assistive ecosystem for the elderly and the vulnerable persons that provides furthermore assistance to the helpers, on-demand medical data and may manage emergency situations. More precisely our goals are to develop devices with the following properties:
- they can be adapted to the end-user and to its everyday environment
- they should be affordable and minimally intrusive
- they may be controlled through a large variety of simple interfaces
- they may eventually be used to monitor the health status of the end-user in order to detect emerging pathology
Assistance will be provided through a network of communicating devices that may be either specifically designed for this task or be just adaptation/instrumentation of daily life objects.
The targeted population is limited to frail people 1 and the assistive devices will have to support the individual autonomy (at home and outdoor) by providing complementary resources in relation with the existing capacities of the person. Personalization and adaptability are key factor of success and acceptance. Our long term goal will be to provide robotized devices for assistance, including smart objects, that may help disabled, elderly and handicapped people in their personal life.
Assistance is a very large field and a single project-team cannot address all the related issues. Hence HEPHAISTOS will focus on the following main societal challenges:
- mobility: previous interviews and observations in the HEPHAISTOS team have shown that this was a major concern for all the players in the ecosystem. Mobility is a key factor to improve personal autonomy and reinforce privacy, perceived autonomy and self-esteem.
- managing emergency situations: emergency situations (e.g. fall) may have dramatic consequences for elderly. Assistive devices should ideally be able to prevent such situation and at least should detect them with the purposes of sending an alarm and to minimize the effects on the health of the elderly.
- medical monitoring: elderly may have a fast changing trajectory of life and the medical community is lacking timely synthetic information on this evolution, while available technologies enable to get raw information in a non intrusive and low cost manner. We intend to provide synthetic health indicators, that take measurement uncertainties into account, obtained through a network of assistive devices. However respect of the privacy of life, protection of the elderly and ethical considerations 7 impose to ensure the confidentiality of the data and a strict control of such a service by the medical community.
- rehabilitation and biomechanics: our goals in rehabilitation are 1) to provide more objective and robust indicators, that take measurement uncertainties into account to assess the progress of a rehabilitation process 2) to provide processes and devices (including the use of virtual reality) that facilitate a rehabilitation process and are more flexible and easier to use both for users and doctors. Biomechanics is an essential tool to evaluate the pertinence of these indicators, to gain access to physiological parameters that are difficult to measure directly and to prepare efficiently real-life experiments.
Addressing these societal focus induces the following scientific objectives:
-
design and control of a network of connected assistive
devices: existing
assistance devices suffer from a lack of essential functions
(communication, monitoring, localization,...) and their acceptance and
efficiency may largely be improved. Furthermore essential functions
(such as fall detection, knowledge sharing, learning, adaptation to
the user and helpers) are missing. We intend to develop new
devices, either by adapting existing systems or developing brand-new
one to cover these gaps. Their performances, robustness and
adaptability will be obtained through an original design
process, called appropriate design, that takes uncertainties
into account to determine almost all the nominal values of the
design parameters that guarantee to obtain the required
performances.
The development of these devices covers our robotics works
(therefore including robot analysis, kinematics, control, ...)
but is not limited to them. These devices will be present in the three
elements of the ecosystem (user, technological helps and
environment) and will be integrated in a common network.
The study of this robotic network and of its element is
therefore a major focus point of the HEPHAISTOS
project. In this field our
objectives are:
- to develop methods for the analysis of existing robots, taking into account uncertainties in their modeling that are inherent to such mechatronic devices
- to propose innovative robotic systems
- evaluation, modeling and programming of assistive ecosystem: design of such an ecosystem is an iterative process which relies on different types of evaluation. A large difference with other robotized environments is that effectiveness is not only based on technological performances but also on subjectively perceived dimensions such as acceptance or improvement of self-esteem. We will develop methodologies that cover both evaluation dimensions. Technological performances are still important and modeling (especially with symbolic computation) of the ecosystem will play a major role for the design process, the safety and the efficiency, which will be improved by a programming/communication framework than encompass all the assistance devices. Evaluation will be realized with the help of clinical partners in real-life or by using our experimental platforms.
- uncertainty management: uncertainties are especially present in all of our activities (sensor, control, physiological parameters, user behavior, ...). We intend to systematically take them into account especially using interval analysis, statistics, game theory or a mix of these tools.
- economy of assistance: interviews by the HEPHAISTOS team and market analysis have shown that cost is a major issue for the elderly and their family. At the opposite of other industrial sectors manufacturing costs play a very minor role when fixing the price of assistance devices: indeed prices result more from the relations between the players and from regulations. We intend to model these relations in order to analyze the influence of regulations on the final cost.
The societal challenges and the scientific objectives will be supported by experimentation and simulation using our development platforms or external resources.
In terms of methodologies the project will focus on the use and mathematical developments of symbolic tools (for modeling, design, interval analysis), on interval analysis (for design, uncertainties management, evaluation), on game theory (for control, localization, economy of assistance) and on control theory. Implementation of the algorithms will be performed within the framework of general purpose software such as Scilab, Maple, Mathematica and the interval analysis part will be based on the existing library ALIAS, that is still being developed mostly for internal use.
Experimental work and the development of our own prototypes are strategic for the project as they allow us to validate our theoretical work and to discover new problems that will feed in the long term the theoretical analysis developed by the team members.
Dissemination is also an essential goal of our activity as its background both on the assistance side and on the theoretical activities as our approaches are not sufficiently known in the medical, engineering and academic communities.
In summary HEPHAISTOS has as major research axes assistance robotics, modeling, game theory, interval analysis, robotics and AI (see section 8.1). The coherence of these axis is that interval analysis is a major tool to manage the uncertainties that are inherent to a robotized device, while assistance robotics provides realistic problems which allow us to develop, test and improve our algorithms. Our overall objectives are presented in this document and in a specific page on assistance.
3 Research program
As seen in the overall objectives managing uncertainties is a key point of our research. In the health domain uncertainties is managed with statistics (which the explain partly presence of E. Wajnberg in our team) but statistics just give trends while in some cases we will be more interested in the worst case scenario. Interval analysis is an approach that can be used in that case and we constantly improve the foundations of this method.
3.1 Interval analysis
We are interested in real-valued system solving (, ), in optimization problems, and in the proof of the existence of properties (for example, it exists such that or it exist two values , such that and ). There are few restrictions on the function as we are able to manage explicit functions using classical mathematical operators (e.g. as well as implicit functions (e.g. determining if there are parameter values of a parametrized matrix such that the determinant of the matrix is negative, without calculating the analytical form of the determinant).
Solutions are searched within a finite domain (called a box) which may be either continuous or mixed (i.e. for which some variables must belong to a continuous range while other variables may only have values within a discrete set). An important point is that we aim at finding all the solutions within the domain whenever the computer arithmetic will allow it: in other words we are looking for certified solutions. For example, for 0-dimensional system solving, we will provide a box that contains one, and only one, solution together with a numerical approximation of this solution. This solution may further be refined at will using multi-precision.
The core of our methods is the use of interval analysis that allows one to manipulate mathematical expressions whose unknowns have interval values. A basic component of interval analysis is the interval evaluation of an expression. Given an analytical expression in the unknowns and ranges for these unknowns we are able to compute a range , called the interval evaluation, such that
In other words the interval evaluation provides a lower bound of the minimum of and an upper bound of its maximum over the box.
For example if and , then , meaning that for any in [0.5,1.6] we guarantee that .
The interval evaluation of an expression has interesting properties:
- it can be implemented in such a way that the results are guaranteed with respect to round-off errors i.e. property 1 is still valid in spite of numerical errors induced by the use of floating point numbers
- if or , then no values of the unknowns in their respective ranges can cancel
- if (), then is positive (negative) for any value of the unknowns in their respective ranges
A major drawback of the interval evaluation is that may be overestimated i.e. values of such that may not exist. This overestimation occurs because in our calculation each occurrence of a variable is considered as an independent variable. Hence if a variable has multiple occurrences, then an overestimation may occur. Such phenomena can be observed in the previous example where while the real maximum of is approximately 0.9144. The value of is obtained because we are using in our calculation the formula with having the same interval value as .
Fortunately there are methods that allow one to reduce the overestimation and the overestimation amount decreases with the width of the ranges. The latter remark leads to the use of a branch-and-bound strategy in which for a given box a variable range will be bisected, thereby creating two new boxes that are stored in a list and processed later on. The algorithm is complete if all boxes in the list have been processed, or if during the process a box generates an answer to the problem at hand (e.g. if we want to prove that , then the algorithm stops as soon as for a certain box ).
A generic interval analysis algorithm involves the following steps on the current box 10, 1:
- exclusion operators: these operators determine that there is no solution to the problem within a given box. An important issue here is the extensive and smart use of the monotonicity of the functions
- filters: these operators may reduce the size of the box i.e. decrease the width of the allowed ranges for the variables
- existence operators: they allow one to determine the existence of a unique solution within a given box and are usually associated with a numerical scheme that allows for the computation of this solution in a safe way
- bisection: choose one of the variable and bisect its range for creating two new boxes
- storage: store the new boxes in the list
The scope of the HEPHAISTOS project is to address all these steps in order to find the most efficient procedures. Our efforts focus on mathematical developments (adapting classical theorems to interval analysis, proving interval analysis theorems), the use of symbolic computation and formal proofs (a symbolic pre-processing allows one to automatically adapt the solver to the structure of the problem), software implementation and experimental tests (for validation purposes).
Important note: We have insisted on interval analysis because this is a major component or our robotics activity. Our theoretical work in robotics is an analysis of the robotic environment in order to exhibit proofs on the behavior of the system that may be qualitative (e.g. the proof that a cable-driven parallel robot with more than 6 non-deformable cables will have at most 6 cables under tension simultaneously) or quantitative. In the quantitative case as we are dealing with realistic and not toy examples (including our own prototypes that are developed whenever no equivalent hardware is available or to verify our assumptions) we have to manage problems that are so complex that analytical solutions are probably out of reach (e.g. the direct kinematics of parallel robots) and we have to resort to algorithms and numerical analysis. We are aware of different approaches in numerical analysis (e.g. some team members were previously involved in teams devoted to computational geometry and algebraic geometry) but interval analysis provides us another approach with high flexibility, the possibility of managing non algebraic problems (e.g. the kinematics of cable-driven parallel robots with sagging cables, that involves inverse hyperbolic functions, see section 8.1.1) and to address various types of issues (system solving, optimization, proof of existence ...). However whenever needed we will rely as well on statistics, continuation, algebraic geometry, geometry while AI is currently being investigated (see section 8.1.2).
3.2 Robotics
HEPHAISTOS, as a follow-up of COPRIN, has a long-standing tradition of robotics studies, especially for closed-loop robots 4, especially cable-driven parallel robots. We address theoretical issues with the purpose of obtaining analytical and theoretical solutions, but in many cases only numerical solutions can be obtained due to the complexity of the problem. This approach has motivated the use of interval analysis for two reasons:
- the versatility of interval analysis allows us to address issues (e.g. singularity analysis) that cannot be tackled by any other method due to the size of the problem
- uncertainties (which are inherent to a robotic device) have to be taken into account so that the real robot is guaranteed to have the same properties as the theoretical one, even in the worst case. This is a crucial issue for many applications in robotics (e.g. medical or assistance robot)
Our field of study in robotics focuses on kinematic issues such as workspace and singularity analysis, positioning accuracy, trajectory planning, reliability, calibration, modularity management and, prominently, appropriate design, i.e. determining the dimensioning of a robot mechanical architecture that guarantees that the real robot satisfies a given set of requirements. The methods that we develop can be used for other robotic problems, see for example the management of uncertainties in aircraft design 8.
Our theoretical work must be validated through experiments that are essential for the sake of credibility and, a contrario, experiments will feed our theoretical work. Hence HEPHAISTOS works with partners on the development of real robots but also develops its own prototypes. In the last years we have developed a large number of prototypes and we have extended our development to devices that are not strictly robots but are part of an overall environment for assistance. We benefit here from the development of new miniature, low energy computers with an interface for analog and logical sensors such as the Arduino or the Phidgets. The web pages presents all of our prototypes and experimental work. Note that this familiarity with hardware is also used from time to time to develop devices for others INRIA projects and during the Covid crisis our building was instrumented for accurately monitoring CO and CO2 level well before it becomes the norm.
4 Application domains
While the methods developed in the project can be used for a very broad set of application domains (for example we have an activity in CO2 emission allowances and biology 11), it is clear that the size of the project does not allow us to address all of them. Hence we have decided to focus our applicative activities on mechanism theory, where we focus on modeling, optimal design and analysis of mechanisms. Along the same line our focus is robotics and especially service robotics which includes rescue robotics, rehabilitation and assistive robots for elderly and handicapped people. Although these topics were new for us when initiating the project we have spent two years determining priorities and guidelines by conducting about 200 interviews with field experts (end-users, doctors, family and caregivers, institutes), establishing strong collaboration with them (e.g. with the CHU of Nice-Cimiez) and putting together an appropriate experimental setup for testing our solutions.
It must be reminded that we are able to manage a large variety of problems in totally different domains only because interval analysis, game theory and symbolic tools provides us the methodological tools that allow us to address completely a given problem from the formulation and analysis up to the very final step of providing numerical solutions. Hence although we mainly focus on medical and assistance robotics we address also a large number of applications: agriculture, biology, arts, system design to name a few.
5 Social and environmental responsibility
5.1 Footprint of research activities
Clearly our activities may have an impact on the environment, especially through travels. We have (an we plan to continue) decreased our travel activities while having reduced our own energy consumption at work in different manners. Still we must emphasize that all aspects of our impact have to be taken into account before coercitive measures are taken. For example when we travel to a retirement house to install assistive devices the footprint impact has to be balanced with the social impact (and this is not an easy task). Furthermore human relationships are essential for initiating new research areas and collaborations and virtual conferences are not very effective for that purpose.
5.2 Impact of research results
Our works on assistance clearly may have a social impact and we are deeply aware of our ethical responsibilities as illustrated by the activity of the team in ethical committees, our collaboration with the academic law community and our large dissemination effort toward the general audience.
Regarding environmental responsibility energy has been since the very beginning of our project an important topic in our research. Indeed our assistance/health monitoring devices require additional energy source and elderly people may have some difficulties to deal with battery charging. Consequently since the beginning of the project we have focused on low consumption electronic components and most our devices use mechanical energy converter to produce a large part of the energy they need. However the intended benefits of these devices on health, self-esteem and dignity (all issues that are difficult to measure/compare in pure financial terms or with respect to environmental impact) have to be taken into account. We have not had a direct activity regarding Covid as our medical research areas are not related to medical modeling or virus. Still to contribute to the collective protection effort we have installed at the end of December 2020 a home-made, low-cost but very accurate CO2 measurement station in our laboratory connect to an aeration system that is still in use after one year of full-time monitoring.
6 Highlights of the year
6.1 Scientific highlights
The highlights of this year are:
- a 4-months deployment of one of our cable-driven parallel robots in a museum for an artistic exhibition (see section 8.1.1)
- some progress in the use of AI for solving robotics kinematic problem. New methodological approaches are investigated as the current tools perform poorly on such a problem (see section 8.1.2)
- a 5-months stay of a team member (E. Wajnberg) at the University of Haifa (see section 8.3)
- the initial step of a team member (Y. Papegay) to create a start-up dealing with human activities recognition using non-intrusive measurements
- Pierre Berthet-Rayne has joined us as a 3IA industrial chair attached to J-P. Merlet senior 3IA chair
Regarding clinical tests the effects of Covid-19 has obliged to postpone once more our planned experiments.
6.2 Institutional life
The HEPHAISTOS team is seriously concerned about heavy dysfunctions in the institute.
- The disastrous failures of the new financial and human resource information system (Eksae) that impacts negatively all administrative colleagues with whom researchers interact. It forces the former to duplicate their works, when not making them unable to perform even simple tasks. It also directly impacts researchers, who cannot oversee their budget in any reliable way, and occasionally have to delay simple purchases as a consequence of a reprioritization of overburdened administrative forces.
- The continuously diminishing emphasis on research in the presentation of Inria and the growing fuzziness around the status of researchers and the role and position of the institute attack the meaning of work and our collective values.
- The extremely degraded relationship between the Inria Commission d’Évaluation and the current Inria direction is unbearable. It causes a general distrust in the direction’s intentions and in the outcome of future hiring and promoting process. The team deplores the current situation. It thanks the Commission d’Évaluation for its outstanding communication to the researchers it represents and for its continued effort in organizing and participating in Inria hiring and promotion committees.
7 New software and platforms
Our activity in AI, which for the time being focus on finding all solutions of a system of equations (see section 8.1.2), has led to numerous software developments (including methodological one) that are yet not still ready to be distributed.
7.1 New software
7.1.1 ALIAS
-
Name:
Algorithms Library of Interval Analysis for Systems
-
Keyword:
Interval analysis
-
Functional Description:
The ALIAS library whose development started in 1998, is a collection of procedures based on interval analysis for systems solving and optimization.
ALIAS is made of two parts:
ALIAS-C++ : the C++ library (87 000 code lines) which is the core of the algorithms
ALIAS-Maple : the Maple interface for ALIAS-C++ (55 000 code lines). This interface allows one to specify a solving problem within Maple and get the results within the same Maple session. The role of this interface is not only to generate the C++ code automatically, but also to perform an analysis of the problem in order to improve the efficiency of the solver. Furthermore, a distributed implementation of the algorithms is available directly within the interface.
- URL:
-
Contact:
Jean-Pierre Merlet
-
Participants:
Jean-Pierre Merlet, Odile Pourtallier
7.2 New platforms
Participants: Jean-Pierre Merlet, Yves Papegay, Romain Tissot.
Vitrifications robot
In 2019 we have used the modularity of our MARIONET-CRANE cable-driven parallel robot (CDPR) prototype to design a robot for the 2-months art exhibition "Vitrifications" with the artist A-V. Gasc. In this exhibition the CDPR acts as a large 3D printing machine that deposit layers of glass micro-beads on a given trajectory over a 21 11 5 meters workspace. Beside the exhibition our scientific interest was to record data on the behavior of our CDPR in a realistic environment by adding to our prototype numerous sensors that were not required for the use of the CDPR but were possibly interesting for monitoring the CDPR state and its environment.
A second prototype was intended to be displayed by the same artist during the 2020 robotics conference ICRA that should have been held in Paris and has been held virtually because of the pandemic. The theoretical modeling, sensing and control of this version has been substantially modified according to the analysis of the 2019 data. Although this CDPR was not deployed a mock-up was installed and used in our laboratory and a second analysis of the data has taken place.
At the end of 2021 we agree with A-V. Gasc to prepare a second exhibition at the Espace de l'Art Concret, a museum close to Sophia that has been held from July 9 to October 16, 2022. This third version has also benefited on all aspects of the 2020-2021 version with a new full theoretical modeling incorporated in the control software while new sensors were added, mostly to monitor the CDPR environment and for the public safety.
We have started analyzing the data provided during the exhibition in order to prepare a new version for the end of 2023 with a different scientific objective: walking assistance and health monitoring for frail people.
8 New results
8.1 Robotics
8.1.1 An exhibition using one of our cable-driven parallel robot
Participants: Jean-Pierre Merlet [correspondant], Yves Papegay, Romain Tissot.
As mentioned in the highlights a major work of the team for 2022 has been the deployment manqueof a large-scale CDPR for a 4 months exhibition in the Espace de l'Art Concret museum2. The used CDPR has 4 cables (synthetic Dyneema of diameter 4mm) that are coiled/uncoiled by winches, the other extremity of the cables being attached at the same point , a drum being attached at this point. This CDPR allows one to control the translational degrees of freedom of the drum.
the photo shows our CDPR prototype
The task of this robot was to deposit several layers of glass micro-beads on a given trajectory at a velocity of 3cm/s, the length of a trajectory being about 30 meters (figure 2).
the photo shows one of the trajectory used for the exhibition
A constant flow of powder is obtained by opening a vane at the bottom of the drum. The CDPR is hence used as a large-scale 3D printer which is a possible

the photo shows the powder flow at the bottom of the drum
market for this type of robot (Y. Papegay have co-founded in 2015 the XtreeE start-up company that is currently one of the leading international actors in large-scale 3D concrete printing).
The robot was installed in a room whose dimensions was 11 8 4.5 meters, which makes this CDPR probably one of the largest 3D printing machine ever built.
After each layer (that requires about 14 kg of powder) the structure below the drum gains some height (about 1.25 mm) but at the same time gains in width (about 3.1 mm) as there is no gluing component in the powder. After depositing over 1 tons of powder the height of the structure is about 9cm for a width of 41cm. As the trajectory is self-intersecting the maximal measured height was about 18cm.

the photo shows part of the printed structure
Although the defined trajectory is planar, the CDPR moves in 3D as the height of the drum was supposed to be constant with respect to the height of the structure under the drum (hence the drum altitude increases at the trajectory self intersecting points). The drum contains about 40 kg of powder for a total weight of about 75 kg and is manually filled after 1 or 2 layers.
During the period the CDPR was under the control of two students of an art school that were executing trajectories according to the public presence. The robot has deposited 176 layers on two trajectories and has used 2.5 tons of powder. Including the travel to the rest position for refilling the drum the robot has traveled about 9 km and has been in use for 126 hours. Over the period there has been 24 intrusions of the public in the robot space, 6 unexplained behavior of the CDPR that has automatically led our safety mechanisms to stop the robot. We have also collected about 2 To of data that will be examined during 2023.
Regarding sensors we have 3 planar lidars on the drum, 2 being horizontal and one vertical. The later one measures the distance between the drum and the structure while the 2 horizontal lidars measure points on the room walls (whose position with respect to the reference frame have been calibrated) which allows to determine the position of in the reference frame. The drum has also a 3 axis accelerometer/gyrometer for measuring the drum oscillations and also an accelerometer on each cable at a fixed distance from . The winches were located on the ground at each corner of the room, the cables going up to a support on the ceiling with a pulley that freely rotates around the vertical axis. We have developed a full model of this system including the pulley (as the cable output point on the pulley changes with the cable direction) and the elastic behavior of the cable which has also its own mass so that the cable shape is not the straight line between the output point on the pulley and (such a cable is called a sagging cable). For modeling such a cable we use the Irvine textbook model 13. This is a non algebraic planar model with the upper attachment point of the cable is supposed to be grounded: it provides the coordinates () of the lowest attachment point of the cable if the cable length at rest and the horizontal and vertical components of the force applied at this point are known.
where is the Young modulus of the cable material, its linear density and the area of a cross-section of the cable.
It may seem that the control law is easy to design as the lidars provide the position of . However the constant drum velocity constraint imposes a velocity control law has to be used. Such a law implies that the desired velocity vector in the reference frame has to be mapped to a velocity for each of the 4 cables. This mapping is linear but the involved matrix are dependent upon the position of and upon the directions of the cables at this point, which in turn change with the length of the cables. Therefore this control law imposes to evaluate the cables lengths . But two factors make the determination of the cable lengths difficult:
- the elasticity of the cable induces a change in the cable length according to its tension
- we are measuring the winch drum rotation velocity with an encoder but this translates into a cable velocity that depends upon the drum radius. As we don't control the coiling process and have several layers on it there is a large uncertainty on the drum radius and therefore on the measurement of the .
Furthermore our CDPR is redundantly actuated (4 actuators for 3 d.o.f) so that we are sure that for a given position of there will be at most 3 cables under tension, the other cable being slack. But it can be shown that there is at least 2 possible triplets of cables that may be under tension at the given position of . Consequently the measurement of the with the encoders is not sufficient to determine the current state of the CDPR but fortunately this indetermination may be solved. Indeed the Irvine model allows one to calculate the slope of the cable at any point and this is where the cable accelerometers play a major role as they provide the cable slope at a known point. Accordingly, we are able to determine which cables are under tension and which one is slack. But the slope measurement plays another role: on an large trajectory the set of 3 cables that are required to be under under tension is different for various parts of the trajectory. Hence on a given part it is acceptable to have a slack cable but its amount of slackness should be small as this cable will have to be taught for the following part of the trajectory. An internal PID controller based on the cable slope is used to regulate the cable slackness. Note that although the system model is quite complex we have designed an algorithm that is able to calculated the cable lengths in about 1ms.
Hence as soon as the lidars provide the location we are able to calculate the cables lengths. But the sampling time of the lidar is about 0.5s while the encoders have a 10 ms sampling time and consequently we use the encoders information to calculate the to control the robot in between two lidar measurements. This imposes to have a good estimation of the drum radius. Up to now we were using a theoretical coiling process model that provides the current drum radius for a given under the assumption that the coiling is ideal, which is a too strong assumption. In the current version of our CDPR we are using another approach. Let assume that two successive measurements of the lidars have provided two set of cable lengths while the encoders have measured the drum rotation angle as at the same time. With these data we are able to calculate a mean value of the drum radius that is used for the control before the next lidar measurement.
As the lidars provide an accurate measurement of the the location of (the lidars being not located at the drum accelerometer data are used to correct the lidar measurement) we have been able to evaluate that the absolute positioning accuracy of the system is about 1 cm which is quite remarkable, especially regarding the size of the workspace. Part of this error is due to the use of flip-flop pulleys as the friction in the pulley axis prohibits the pulley to lie exactly in the right plane, thereby introducing a bias in estimation of the cable lengths. Previously we were using a pin-hole output through a low friction material that surprisingly was exhibiting a very low wear after months of use, even with metallic cables and we will come back to this solution for the next version.
A scientific side interest of this experiment is that we are using the vertical lidar to perform every 2 seconds a planar vertical scans of the structure when the CDPR is executing a trajectory, so that we are able to obtain a full 3D model of the structure after each layer. Before the exhibition we have been in touch with researchers working in granular mechanics (e.g. for dune or avalanche modeling). They were able to predict very well the overall shape of the structure for the regular part of the trajectory but have more difficulty at the self-intersecting points. Such an experiment is interesting for these researchers as we have here a well-controlled experiment with not external disturbances (such as wind), an exact knowledge of the powder flow, an homogeneous material, the possibility of repeating an experiment and an accurate 3D model.
8.1.2 AI
As seen in section 8.1.1 we have a complex model of our system but this is not a problem for control as we have been able to design very fast algorithms for dealing with the inverse kinematics problem (IK: find the cable lengths to reach a given position for the CDPR) and for the direct kinematics problem (DK: find the robot position being given the cable lengths ).
But the IK and DK are important not only for control but also for design. In the design phase we have to be able to determine all IK/DK solutions over a given workspace, for example for determining what will be the maximal cable tensions and consequently the minimal cable diameter such that the cable can sustain the maximal tension. Additionally we have to determine the maximal torque applied on the drum in order to calculate what should be the maximal winch motor torque.
Finding this maximal tension/maximal drum torque over a given workspace are difficult constrained optimization problems that can be solved exactly for simple CDPRs and cable models but has no known solution for our prototypes.
In this case it is usual to discretize the workspace and to calculate the cable tensions over a large set of pose (if the workspace is defined in terms of possible poses) or a large set of cables lengths. This means that we have to solve either the IK or DK a large number of time. Unfortunately in our case both the IK and DK have multiple solutions. When in use the robot state for a given set of is unique and depends upon the CDPR motion history. In the design phase we have to adopt a worst case scenario and consider all possible cases, thereby considering all possible IK/DK solutions. We will now focus on the DK problem. Obtaining the DK solutions amounts for a CDPR with cables to solve a square system of equations (the Irvine equations and the 6 mechanical equilibrium equations) involving the pose of the robot (defined by 6 unknowns) and the horizontal and vertical components of the tensions in the cables at the attachment points on the platform.
If sagging cables are considered we are the only team that has been able to design algorithms, denoted exact, that are able to calculate all the IK and DK solution either by using a continuation process or an interval analysis approach 15,5. Unfortunately these algorithms are computer intensive (one hour for the IK and much more for the DK, that may have between 10 and 50 solutions) and are therefore not appropriate for the design phase which require to solve these problems a very large number of time.
In 2021 we have considered using AI to solve the DK problems using a Multi-Layer Perceptron (MLP) but we were surprised that solving a system of equations was a topic that is barely addressed in the AI community (with a few exceptions). Since the start we were aware of two possible problems:
- a MLP is able to provide a single output while we have multiple solutions
- the DK system is what we called a double stiff system, meaning that for a sufficiently large ball in the space we have a smooth region where small changes in the induce small changes in the solution while we have also stiff regions where the solution changes are high and even stiffer region with extremely large changes
- we were not expecting exact solutions but an error of 1% was deemed to be acceptable
We have first shown that it was possible to construct an arbitrarily large training set for the MLP based on the IK and DK solutions that has been computed by the exact algorithms for a few selected cases ( we have provided open-source learning databases in 14). We have then to determine the geometry of the MLP, i.e. the number of hidden layers, the number of neurons in each layer, the activation function(s) and the loss function After a few preliminary trials we noticed that
- the learning time was small (a few minutes)
- having large values for does not significantly change the final value of the loss function
- a set of 5 possible activation function were providing the best final loss
- the MSE loss was the most efficient loss function
Based on there remarks we systematically explore all possible combinations of values for (in the set [2,200]), (in [10,200]) and the set of 5 activation functions. We hence create a large number of MLPs with the hope to obtain MLPs providing different solutions for a given set of . The results were poor: even the best MLPs were giving the solution with 200% of error on the output for the training set and 300% on a verification set.
We then consider using a hybridization approach: the MLP prediction is used as initial guess for the Newton method which, if convergent, provides an exact solution. This has led to a small improvement as about 5% of the total number DK solutions were found but we also noticed that even if the Newton scheme was converging for several MLPs, they all provide the same DK solution.
We also noticed key points occurring during the optimization of the loss function:
- a decrease of the loss function does not automatically implies an increase of the number of Newton convergence for the current model
- some MLPs were exhibiting quite good predictions on some variables especially the and very poor predictions on the other variables
Point 1 can be explained because of the behavior of the Newton scheme that converges if there is good prediction for some part of the variables, called essential, while the accuracy of the prediction is much less important for the remaining variables (the non-essential one). A decrease of the loss function may be obtained if the errors on the non-essential variables are significantly decreasing while we have a limited increase on the errors of the essential variables, which lead to a decrease of the number of Newton convergences. Points 1 and 2 lead us to change our methodology to exploit AI:
- the number of convergences is calculated after each significant change of the loss function and we store the MLP (denoted type 1 MLP) having exhibited the largest number of convergences
- the MLPs, denoted type 2 MLP, leading to the lowest MSE for each is stored.
We therefore end up with several type 1 and 2 MLPs. When checking the verification set we use first the predictions of the type 1 MLPs as guess for the Newton scheme. Then we create new guesses for the Newton scheme by updating the type 1 MLP prediction on the by the one obtained for the type 2 MLPs.
A second change is the clusterization of the training set. For that purpose the ranges for the output variables over the whole training set have been split in smaller components and we have found out that with 12 sets of ranges for the variables we were able to cover the whole training set. A cluster is obtained as all the elements of the training set whose output belongs to the same . The MLP training is then performed for each cluster so that we get about 4000 MLPs. Checking the verification set is done by using all these MLPs3 12,3. About 30% of the DK solutions were obtained with this approach and in a very few cases we have been able to obtain 2 DK solutions for a given set of . Although this is a progress, we are still quite far from a good result, especially regarding the very low number of DK solutions we get for a given set of .
We plan to investigate the following methodological improvements:
- using Physics-informed neural network (PINN): as seen previously the MSE loss is not the most appropriate loss function for our case. With the help of the 3IA techpool we are implementing a MLP builder where the loss function is based on the absolute value of the DK equations, thereby moving partly to unsupervised learning, although the quality of the MLP may have still to rely on the number of Newton convergences over a training set. This is a preliminary trial but later on we may consider minimizing the Kantorovitch index (that uses the norms of the equations vector and of the system Jacobian and Hessian matrix) which, if lower than 1 ensures the convergence of the Newton scheme
- modifying our cluster algorithm using an idea based on the concept of kinematic branches. Assume that all DK solutions (i.e. points in the output space ) have been obtained for a given set of i.e. a point in the -dimensional space . If the point follows a path in , then each DK solution follows a path in which is a kinematic branch. The training clusters are now designed to contain only elements that lie on the same kinematic branch. Preliminary tests on one of such a cluster have shown that the learning allows to obtain MLPs that have an almost 100% Newton converge rate for the training set. It remains to verify that this is the case for all clusters and then to test the MLPs on an arbitrary verification set
- using dimension reduction: in the DK problem if we have a prediction for the location of the platform, then the Irvine equations for a given cable is a system of 2 equations in the unknown that has a unique solution (although we have not found any formal proof for this point). Provided that we have a numerical procedure to solve these equations we may reduce the DK MLP output dimension to 6 but still use the calculated cables in the loss function. Regarding the Newton scheme we already know that the Irvine equations are satisfied so that will remain only the 6 mechanical equilibrium equations, A possible consequence of this situation may be that the Newton convergence ball will be larger thereby allowing a larger number of Newton convergence over the verification set. We have already designed MLPs for solving the 2 Irvine equations with good success and we plan to design a safe algorithm for this solving, possibly mixing MLPs and deterministic methods
Provided that we are able to design MLPs that have a good success rate for determining all DK solutions we are also planning to address the issue of using discretization. Indeed we are not completely satisfied with the result as we have sampled the space so that we may have missed the real maximum tension (and remembering the double stiffness of the system there may be a severe error on the maximal tension). For addressing this issue we plan to design a growing algorithm: the idea is basically to obtain an accurate upper bound of the cable tensions for balls centered at the points of used in the discrete treatment. For a given there are methods (namely the Kantorovitch theorem and Neumaier inflation method) that allow one to calculate a ball in the space, centered at , such that we are sure that all DK solutions for the in the ball are enclosed in known balls. With this method we will be able to determine a safe upper bound for the cables tensions over a ball in the space and if we are able to fully cover the desired region in the with such balls, then we will obtain a safe bound for the tensions over the whole region.
8.2 Medical activities
As all of our clinical trials scheduled for 2020-2021 have been either canceled or postponed because of the pandemic we have used 2021 to develop new devices that were planned for later on. Still we have had restriction for on-site access that have penalized these developments.
8.2.1 Modular rehabilitation station
Rehabilitation is also a major topic of the team. The medical community has indicated to us several major issues with commercially available rehabilitation devices: difficulty to configure the device for training a given musculo-squelettic group which impose a persistent action to the ergotherapeuthe and therefore divert him from observing the patient, the lack of synthetic indicators to assess the rehabilitation efficiency, the lack of modularity and of mobility help that complicates the ergotherapeuthe task when the patient motricity is not yet sufficient, the lack of motivation stimulus for the patient, a large setup time for installing the patient in the device and finally the cost of the devices. To address these problems we start developing a modular rehabilitation station which is first able to manage different types of training devices (illustrated with a treadmill in figure 5 but a rower or an equilibrium station are also available). The training devices of the station are actuated: for example we can change the slope and inclination of the treadmill which allow to adjust the difficulty level of the exercise but also to favor the work of specific musculo-squelettic groups. Furthermore a CDPR (see next section) is able to exert a vertical lifting force that allows to start a rehabilitation process even with a patient that is not yet able to stand up on his own. Regarding the patient motivation the patient is immersed in a virtual environment that makes the patient more comfortable but also allows for a replay of an exercise: on the figure the patient is walking in a mountainous environment whose slope is completely or partially reflected by the treadmill. Finally the patient body configuration during the exercise is measured by using several external sensors (lidars, accelerometers, ...) while, if necessary, the support force that he requires is measured by the CDPR and/or by force sensors in the handle (which allow also to estimate his stress). Using this external measurements allows for a minimal setup time and pertinent medical indicators are deduced from these measurements (for example for the treadmill we measure the number of steps, the leg velocities and poses, the patient trajectory deviation,...). Consequently the main task for the ergotherapeuthe is to adjust the difficulty level and to observe the patient during the exercise while a complete set of medical indicators will be provided at the end of the exercises.

The photo shows the overall set of the rehabilitation station with a treadmill and a virtual reality screen
The rehabilitation station
8.2.2 Human activity recognition
Participants: Jean-Pierre Merlet, Yves Papegay, Odile Pourtallier, Eric Wajnberg.
Human activity recognition (HAR) is a major topic in the team. We are focusing on monitoring mobility and displacements (we are not interested in recognizing the individual action of our subject) using a sensor-based approach, excluding vision which is intrusive and even prohibited in some places for legal reasons. For that purpose we have developed a smart barrier combining redundant passive infrared motion detectors and infrared distance sensors. Smart barriers have been implemented in Ehpad Valrose, a new retirement house in which a specific infrastructure has been put in place to accommodate research works and in Institut Claude Pompidou, a Alzheimer day care hospital from 2019 to 2020. These two long term experiments has allowed us to determine that essential points in HAR are to determine what is possible to measure, the sensor types, how to retrieve and process sensor data, how effective are the quality of measurements on a long term basis and the level of monitoring that is acceptable for frail peoples and their helpers while providing significant and reliable data for the medical community in spite of the uncertainties both in the measurements and in the system modeling. These samples of questions will become central in our work. Unfortunately the pandemic has prohibited us to improve our smart barriers and to test a new version.
8.3 Biology activities
Participants: Eric Wajnberg, Yves Papegay, Odile Pourtallier.
8.3.1 Optimized flower visiting strategy of bees
As explained in the previous activity report, an international scientific cooperation was launched in 2020 with Israeli scientists located at the University of Haifa to understand the optimal foraging decision of bees foraging for nectar. We developed an optimization deterministic model trying to understand what should be the optimized flower visiting strategy, taking into account the ability of the foraging animals to learn the quality of the different flowers they are visiting. This work was continued in 2022, adding more realistic features to the model, and the results obtained were presented in international conferences, and were accepted for publication in a top-level international journal on animal ecology and behavior. The results we obtained are providing a couple of predictions that are now being tested on real animals in the University of Haifa in Israel, through a contact our Israeli partners were able to obtain. Future developments are planned.
8.3.2 Optimal reproductive strategy
In 2021, we developed an international scientific cooperation with Italian scientists located at the University Palermo, Sicily. The goal was to develop a mechanistic and probabilistic model whose aim was to understand the optimal reproductive strategy adopted by two competing insect wasp species (called Trissolcus basalis, abbreviated here as “Tb”; and Ooencyrtus telenomicida abbreviated here as “Ot”) both laying their eggs (and thus killing) the eggs of the stink bug Nezara viridula. In entomology, the competition between different species is called either “extrinsic”, when the competition occurs between females laying their eggs, or “intrinsic”, when the competition occurs between their progeny developing within the same host. On this specific biological system, Tb is known to be a better extrinsic competitor, while Ot is better to win the intrinsic competition when the progeny of the two species are developing within the same host. Tb females are also known to produce an overall higher number of eggs during their lifetime (higher overall fecundity). Nezara viridula eggs are laid in so-called egg- masses that can have different size, and the size of the egg masses attacked by the two competing wasp species should play a role in the global output and success of the two species. For example, on small egg masses, the proportion of eggs attacked by both species will increase which should give an advantage for Ot, while the opposite is expected on larger egg masses. In this context, we developed a model trying to identify what are the environmental conditions that should promote one competing species over the other. Figure 6 gives an example of the type of results obtained.
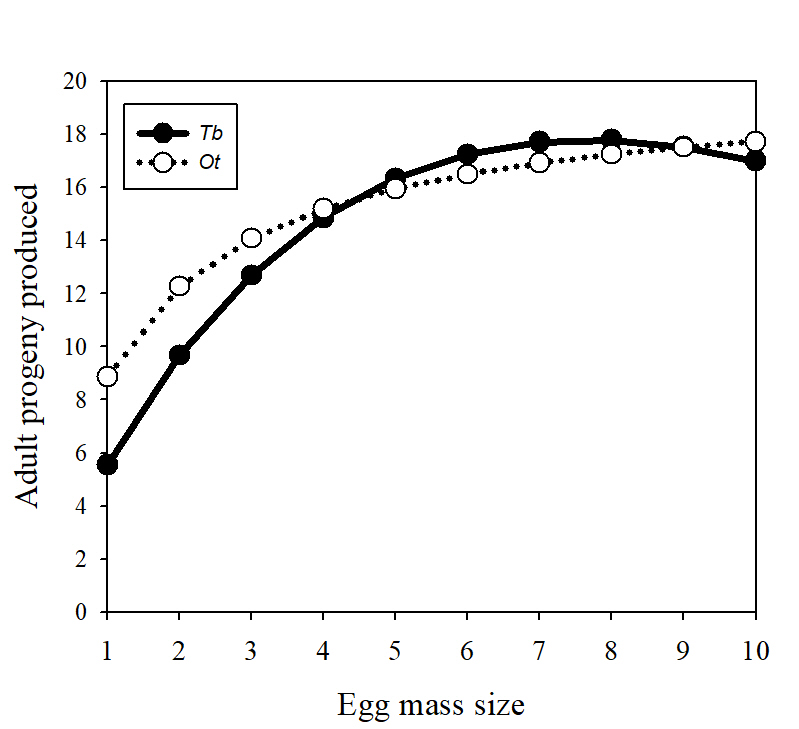
The figures shows the progeny for species Tb and Ob according to the egg mass size
Progeny produced by the two competing species attacking hosts eggs grouped in different egg mass sizes, as predict by the theoretical model developed. On small egg mass sizes, an important proportion of hosts are attacked by both species, and Ot wins the competition since it is a better intrinsic competitor. When the size of the egg mass increases, Tb starts to win the competition since females are better extrinsic competitor and have an overall higher fecundity. When egg mass sizes become even bigger, Tb start to lose the competition because females cannot control all hosts available and they lose the competition in the hosts in which they develop simultaneously with Ot progeny.
9 Partnerships and cooperations
Participants: Jean-Pierre Merlet, Yves Papegay, Odile Pourtallier, Eric Wajnberg.
9.1 International initiatives
9.1.1 Participation in other International Programs
Participants: Eric Wajnberg.
- Title: Mathematical modeling of biological control interaction to support agriculture and conservation
- Financially supported by the IIAS (Israel Institute for Advanced Studies)
- International Research group of 20 persons
- E. Wajnberg is co-supervisor of this program
- Duration: 5 months
9.2 International research visitors
9.2.1 Visits to international teams
Research stays abroad
- E. Wajnberg has visited U. Haifa for 5 months
9.2.2 Other european programs/initiatives
- Hephaistos is part of the euROBIN, the Network of Excellence on AI and robotics that was launched in 2021
9.3 National initiatives
- Hephaistos is part of the EquipEx+ AMI dealing with XXL robots
- project Craft on collaborative cable-driven parallel robot funded by ANR. It involves LS2N (Nantes) and the Cetim. This project has started beginning of 2019.
10 Dissemination
Participants: Jean-Pierre Merlet, Odile Pourtallier, Yves Papegay, Eric Wajnberg.
10.1 Promoting scientific activities
We will not mention our review activity which is quite large but part of the job.
10.1.1 Scientific events: organisation
- J-P. Merlet is a permanent member of the International Steering Committee of the IROS conference, of the CableCon conference and chairman of the scientific Committee of the Computational Kinematics workshop. He was also an advisor for the largest robotics conference ICRA 2020, that has finally being held virtually because of the Covid,
- Y. Papegay is a permanent member of the International Steering Committee of the International Mathematica Symposium conferences series. He is a member of the OpenMath Society, building an extensible standard for representing the semantics of mathematical objects.
10.1.2 Journal
- E. Wajnberg is Editor-in-Chief of the international journal “BioControl” since September 2006, a member of the Editorial Board of the international journal “Entomologia Experimentalis et Applicata”, since 1996, a member of the Editorial Board of the international journal “Applied Entomology and Zoology”, since 2003 and a member of the Editorial Board of the international journal “Neotropical Entomology”, since 2009.
10.1.3 Invited talks
- J-P. Merlet gives a talk about AI during an INRIA/OCA seminar. He gives a presentation about assistance during the Healthy EUR seminar
- E. Wajnberg has given an invited talk at the Symposium “Models for biological control”, International Congress of Entomology. Helsinki, Finland. July.
10.1.4 Leadership within the scientific community
- J-P. Merlet is a member of the IFToMM (International Federation for the Promotion of Mechanism and Machine Science) technical Committees on History and on Computational Kinematics. He is a member of the IFToMM Executive Council Publication Advisory Board and an IEEE Fellow. He is a member of the scientific committee of the CNRS GDR robotique and a senior chair of 3IA Côte d’Azur.
10.1.5 Scientific expertise
- J-P. Merlet is a Nominator for the Japan’s Prize and the head of the robotics GDR Publication Committee in charge of producing a report on "recommended supports for publication" for journals and conferences that does not provide a ranking but advices according to robotics topics
- E. Wajnberg is an appointed member of the Academic Committee of the Hebrew University of Jerusalem, since June 2022, for four years and an appointed member of the International Advisory Board of the “International Center for Excellence in Biological Control”, from August 2018 to August 2023.
10.1.6 Research administration
- J-P. Merlet is a corresponding member of INRIA ethical committee (COERLE) and member of the Ethical Committee of Université Côte d’Azur (CER). He is an elected member of INRIA Scientific Committee. As 2022 was an evaluation year for the INRIA robotics teams he was the coordinator of a prospective report of the teams. He was a member of the 2022 local jury for the hiring of new INRIA researchers
- Y.Papegay is the president of Comité des Utilisateurs des Moyens Informatiques
- O. Pourtallier is a substitute board member of SeaTech, an Engineering School of University of Toulon. She is member of the NICE committee (long term invited scientists and post-doctoral student selection) and of the Transform committee of INRIA Sophia-Antipolis.
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- J-P. Merlet has taught 15 hours on parallel robots to Master ISC (M2) at University of Toulon.
- O. Pourtallier lectured 6 hours on game theory to Master OSE (M2), at École des Mines de Paris, Sophia Antipolis, France.
- E. Wajnberg teaches 60h at The Hebrew University of Jerusalem and University of Sao Paulo - Piracicaba, Brazil.
10.2.2 Supervision
- J-P. Merlet is the supervisor for the PhD of R. Tissot
- Y. Papegay is the supervisor of the CIFRE PhD of Alexandre Tran
10.2.3 Juries
- J-P. Merlet has been president of the jury of the PhD thesis of B. Fasquelle (LS2N, Nantes) and a member of the Best Thesis Award of the robotics GDR
10.3 Popularization
- J-P. Merlet and E. Wajnberg gives talks in the Alpes-Maritimes in the framework of the Science pour Tous association.
- J-P. Merlet and Y. Papegay are active members of the dissemination organization Terra Numerica
10.3.1 Interventions
- J-P. Merlet and E. Wajnberg give two talks at the INRIA Cafe-In seminar
- J-P. Merlet give a general INRIA talk about Hephaistos activities regarding handicap and a presentation of our 3D printing robot during the Fête de la Science
11 Scientific production
11.1 Major publications
- 1 articleInterval Analysis and Reliability in Robotics.International Journal of Reliability and Safety32009, 104-130URL: http://hal.archives-ouvertes.fr/inria-00001152/en/
- 2 inproceedingsMaximal cable tensions of a N-1 cable-driven parallel robot with elastic or ideal cables.CableCon 2021 - 5th International Conference on Cable-Driven Parallel RobotsVirtual, FranceJuly 2021
- 3 inproceedingsMixing AI and deterministic methods for the design of a transfer system for frail people.Sophia IAsummitSophia-Antipolis, FranceNovember 2021
- 4 bookParallel robots, 2nd Edition.Springer2005
- 5 inproceedingsThe kinematics of cable-driven parallel robots with sagging cables: preliminary results.ICRA 2015 - IEEE International Conference on Robotics and AutomationSeattle, United States2015, 1593-1598
- 6 inproceedingsUsing interval analysis in robotics problems.SCANTokyo, JapanSeptember 2018
- 7 articleLes avancées en robotique d'assistance à la personne sous le prisme du droit et de l'éthique.Revue générale de droit médicaleDecember 2017
- 8 phdthesisDe la modélisation littérale à la simulation certifiée.Université de Nice Sophia-AntipolisNice, FranceJune 2012, URL: http://tel.archives-ouvertes.fr/tel-00787230
- 9 inproceedingsFrom Modeling to Simulation with Symbolic Computation: An Application to Design and Performance Analysis of Complex Optical Devices.Proceedings of the Second Workshop on Computer Algebra in Scientific ComputingMunichSpringer VerlagJune 1999
- 10 inproceedingsA Polynomial Time Local Propagation Algorithm for General Dataflow Constraint Problems.Proc. Constraint Programming CP'98, LNCS 1520 (Springer Verlag)1998, 432--446
11.2 Publications of the year
International journals
International peer-reviewed conferences
11.3 Cited publications
- 13 bookCable Structures.MIT Press1981
- 14 miscData base for the direct kinematics of cable-driven parallel robot (CDPR) with sagging cables.These databases provide learning and verification sets that may used by AI to solve the direct kinematics of a cable-driven parallel robot with 8 cables. The input of this problem is the lengths of th 8 cables and the output should be all platform poses that are compatible with the cable lengths. The cable model that is used is the full model (elasticity and cable mass) that can be foud in Irvine textbook.December 2021
- 15 conferencePreliminaries of a new approach for the direct kinematics of suspended cable-driven parallel robot with deformable cables.EucomesNantes2016

