Keywords
Computer Science and Digital Science
- A2.1.3. Object-oriented programming
- A2.1.4. Functional programming
- A2.4.3. Proofs
- A6.1.1. Continuous Modeling (PDE, ODE)
- A6.1.4. Multiscale modeling
- A6.1.5. Multiphysics modeling
- A6.2.1. Numerical analysis of PDE and ODE
- A6.2.5. Numerical Linear Algebra
- A6.2.8. Computational geometry and meshes
- A6.3.1. Inverse problems
- A6.3.4. Model reduction
- A6.3.5. Uncertainty Quantification
Other Research Topics and Application Domains
- B3.1. Sustainable development
- B3.3.1. Earth and subsoil
- B3.4.2. Industrial risks and waste
- B3.4.3. Pollution
- B4.1. Fossile energy production (oil, gas)
- B4.2.1. Fission
- B5.5. Materials
1 Team members, visitors, external collaborators
Research Scientists
- Martin Vohralík [Team leader, INRIA, Senior Researcher, HDR]
- François Clément [INRIA, Researcher]
- Zhaonan Dong [INRIA, Researcher]
- Alexandre Ern [ENPC, Senior Researcher, HDR]
- Gregor Gantner [Inria, ISFP, from Nov 2022]
- Michel Kern [INRIA, Researcher]
- Géraldine Pichot [INRIA, Researcher]
Post-Doctoral Fellows
- Manuela Bastidas Olivares [INRIA, until Mar 2022]
- Akram Beni Hamad [INRIA, from Oct 2022]
- André Harnist [INRIA]
PhD Students
- Joëlle Ferzly [IFP Energies Nouvelles, until Oct 2022]
- Romain Mottier [CEA]
- Houda Mouhcine [Université Paris-Saclay]
- Idrissa Niakh [EDF]
- Stefano Piccardo [ENPC (until April 2021) and UPC (since May 2021), until Sep 2022]
- Ari Rappaport [INRIA]
- Morgane Steins [CEA]
- Zuodong Wang [INRIA, from Oct 2022]
- Daniel Zegarra Vasquez [INRIA]
Technical Staff
- Sébastien Furic [INRIA, Engineer]
- Simon Legrand [INRIA, Engineer]
Interns and Apprentices
- Dania Khiralla [Inria, Intern, from Jun 2022 until Aug 2022]
- Zuodong Wang [INRIA, Intern, from May 2022 until Sep 2022]
Administrative Assistant
- Derya Gök [INRIA]
Visiting Scientists
- Johnny Guzmán [Brown University, from Oct 2022 until Oct 2022]
- Koondanibha Mitra [Radboud University Nijmegen, from Mar 2022 until Mar 2022]
- Jan Papez [Czech Academy of Sciences, from Jun 2022 until Jun 2022]
- Iuliu Pop [Hasselt University, from Oct 2022 until Oct 2022, HDR]
- Fabio Vicini [ECOLE POLYTECHNIQUE TURIN, from Nov 2022]
External Collaborators
- Guy Chavent [retired from Inria, HDR]
- Guillaume Delay [Sorbonne université, from Jul 2022]
- François Delebecque [retired from Inria]
- Jérôme Jaffré [retired from Inria, HDR]
- Caroline Japhet [Sorbonne Paris Nord]
- Habib Jreige [SciWorks]
- Vincent Martin [Université de Technologie de Compiègne]
- Jean Roberts [retired from Inria, HDR]
- Pierre Weiss [retired from Inria]
2 Overall objectives
The project-team SERENA is concerned with numerical methods for environmental problems. The main topics are the conception and analysis of models based on partial differential equations, the study of their precise and efficient numerical approximation, and implementation issues with special concern for reliability and correctness of programs. We are in particular interested in guaranteeing the quality of the overall simulation process. SERENA has taken over the project-team POMDAPI2 which ended on May 31, 2015. It has been given an authorization to become a joint project-team between INRIA and ENPC at the Committee of Projects, September 1st, 2016, and was created as project-team on April 10, 2017.
3 Research program
3.1 Multiphysics coupling
Within our project, we start from the conception and analysis of models based on partial differential equations (PDEs). Already at the PDE level, we address the question of coupling of different models; examples are that of simultaneous fluid flow in a discrete network of two-dimensional fractures and in the surrounding three-dimensional porous medium, or that of interaction of a compressible flow with the surrounding elastic deformable structure. The key physical characteristics need to be captured, whereas existence, uniqueness, and continuous dependence on the data are minimal analytic requirements that we seek to satisfy. At the modeling stage, we also develop model-order reduction techniques, such as the use of reduced basis techniques or proper generalized decompositions, to tackle evolutive problems, in particular in the nonlinear case, and we are also interested in developing reduced-order methods for variational inequalities such as those encountered in solid mechanics with contact and possibly also friction.
3.2 Advanced numerical discretization methods
We consequently design numerical methods for the devised model, while focusing on enabling general polytopal meshes, in particular in response to a high demand from our industrial partners (namely EDF, CEA, and IFP Energies Nouvelles). We in particular promote structure-preserving approaches that mimic at the discrete level the fundamental properties of the underlying PDEs, such as conservation principles and preservation of invariants. We perform numerical analysis in particular in singularly perturbed, unsteady, and nonlinear cases (reaction–diffusion and wave problems, eigenvalue problems, interface problems, variational inequalities, contact problems, degenerate parabolic equations), we apply these methods to challenging problems from fluid and solid mechanics involving large deformations, plasticity, and phase appearance and disappearance, and we develop a comprehensive software implementing them.
3.3 Domain decomposition and Newton–Krylov (multigrid) solvers
We next concentrate an intensive effort on the development and analysis of efficient solvers for the systems of nonlinear algebraic equations that result from the above discretizations. We have in the past developed Newton–Krylov solvers like the adaptive inexact Newton method, and we place a particular emphasis on parallelization achieved via the domain decomposition method. Here we traditionally specialize in Robin transmission conditions, where an optimized choice of the parameter has already shown speed-ups in orders of magnitude in terms of the number of domain decomposition iterations in model cases. We concentrate in the SERENA project on adaptation of these algorithms to the above novel discretization schemes, on the optimization of the free Robin parameter for challenging situations, and also on the use of the Ventcell transmission conditions. Another feature is the use of such algorithms in time-dependent problems in space-time domain decomposition that we have recently pioneered. This allows the use of different time steps in different parts of the computational domain and turns out to be particularly useful in porous media applications, where the amount of diffusion (permeability) varies abruptly, so that the evolution speed varies significantly from one part of the computational domain to another. Our new theme here are Newton–multigrid solvers, where the geometric multigrid solver is tailored to the specific problem under consideration and to the specific numerical method, with problem- and discretization-dependent restriction, prolongation, and smoothing. Using patchwise smoothing, we have in particular recently developed a first multigrid method whose behavior is both in theory and in practice insensitive of (robust with respect to) the approximation polynomial degree. With patchwise techniques, we also achieve mass balance at each iteration step, a highly demanded feature in most of the target applications. The solver itself is then adaptively steered at each execution step by an a posteriori error estimate (adaptive stepsize, adaptive smoothing).
3.4 Reliability by a posteriori error control
The fourth part of our theoretical efforts goes towards guaranteeing the results obtained at the end of the numerical simulation. Here a key ingredient is the development of rigorous a posteriori estimates that make it possible to estimate in a fully computable way the error between the unknown exact solution and its numerical approximation. Our estimates also allow to distinguish the different components of the overall error, namely the errors coming from modeling, from the discretization scheme, from the nonlinear (Newton) solver, and from the linear algebraic (Krylov, domain decomposition, multigrid) solver. A new concept here is that of local stopping criteria, where all the error components are balanced locally within each computational mesh element. This naturally connects all parts of the numerical simulation process and gives rise to novel fully adaptive algorithms. We also theoretically address the question of convergence of the new fully adaptive algorithms. We identify theoretical conditions so that the error diminishes at each adaptive loop iteration by a contraction factor and we in particular derive a guaranteed error reduction factor in model cases. We have also proved a numerical optimality of the derived algorithms in model cases in the sense that, up to a generic constant, the smallest possible computational effort to achieve the given accuracy is needed.
3.5 Safe and correct programming
Finally, we concentrate on the issue of computer implementation of scientific computing programs, noting that precise numerical simulation and guaranteed error estimation are impossible without correct computer implementation. With their increasing complexity, it becomes a major challenge to implement up-to-date scientific computing algorithms using traditional methods and languages. Fortunately, the computer science community has already encountered similar issues, and offers theoretically sound tools for safe and correct programming. We use these tools to design generic solutions for the implementation of the class of scientific computing software the project-team is dealing with. Our focus ranges from high-level programming with OCaml for the precious safety guards provided by its type system and for its ability to encourage functional programming, to proofs of correctness of numerical algorithms and programs, including bounds of the round-off errors, via mechanical proofs with Coq.
4 Application domains
4.1 Multiphase flows and transport of contaminants in the subsurface
- subsurface depollution after chemical leakage
- nuclear waste disposal in deep underground repositories
- flow in large scale discrete fracture networks
- production of oil and gas
4.2 Industrial risks in energy production
- Stokes and Navier–Stokes flows related to nuclear reactor operation
- seismic wave propagation for detection and protection
- electromagnetism for interfaces between dielectrics and negative metamaterials
4.3 Nonlinear mechanics
- quasi-static and dynamic elastoplastic evolutions with small and large deformations
- quasi-static and dynamic crack propagation
- nonlinear contact and friction conditions
- application to engineering components mainly related to nuclear reactor operation and safety analysis
4.4 Computational quantum chemistry
- guaranteed bounds for ground-state energy (eigenvalues) and ground-state density matrix (eigenvectors) in first-principle molecular simulation
- application to Laplace, Gross–Pitaevskii, Kohn–Sham, and Schrödinger models
5 Social and environmental responsibility
5.1 Impact of research results
Via applications with our industrial and environmental partners EDF, CEA, IFP Energies Nouvelles, ANDRA, ITASCA, and BRGM.
6 Highlights of the year
The ERC GATIPOR project has been finished by the concluding international workshop. We have organized the 2022 CEA–EdF–Inria summer school on Certification of errors in numerical simulations.
7 New software and platforms
7.1 New software
7.1.1 DiSk++
-
Name:
Discontinuous Skeletal C++ Library
-
Keywords:
High order methods, Polyhedral meshes, C++
-
Scientific Description:
Discontinuous Skeletal methods approximate the solution of boundary-value problems by attaching discrete unknowns to mesh faces (hence the term skeletal) while allowing these discrete unknowns to be chosen independently on each mesh face (hence the term discontinuous). Cell-based unknowns, which can be eliminated locally by a Schur complement technique (also known as static condensation), are also used in the formulation. Salient examples of high-order Discontinuous Skeletal methods are Hybridizable Discontinuous Galerkin methods and the recently-devised Hybrid High-Order methods. Some major benefits of Discontinuous Skeletal methods are that their construction is dimension-independent and that they offer the possibility to use general meshes with polytopal cells and non-matching interfaces. The mathematical flexibility of Discontinuous Skeletal methods can be efficiently replicated in a numerical software: by using generic programming, the DiSk++ library offers an environment to allow a programmer to code mathematical problems in a way completely decoupled from the mesh dimension and the cell shape.
-
Functional Description:
The software provides a numerical core to discretize partial differential equations arising from the engineering sciences (mechanical, thermal, diffusion). The discretization is based on the "Hybrid high-order" or "Discontinuous Skeletal" methods, which use as principal unknowns polynomials of arbitrary degree on each face of the mesh. An important feature of these methods is that they make it possible to treat general meshes composed of polyhedral cells. The DiSk ++ library, using generic programming techniques, makes it possible to write a code for a mathematical problem independently of the mesh. When a user writes the code for his problem using the basic operations offered by DiSk ++, that code can be executed without modifications on all types of mesh already supported by the library and those that will be added in the future.
- URL:
- Publication:
-
Author:
Matteo Cicuttin
-
Contact:
Matteo Cicuttin
-
Partner:
CERMICS
7.1.2 ParaCirce
-
Name:
Parallel Circulant Embedding
-
Keywords:
2D, 3D, Hydrogeology, Gaussian random fields, MPI
-
Scientific Description:
ParaCirce implements the algorithm proposed by [C. R. Dietrich and G. N. Newsam. A fast and exact method for multidimensional gaussian stochastic simulations. Water Resources Research, 29(8):2861-2869, 1993] as well as an algorithm to accelerate the padding estimation [Pichot et al. SMAI Journal of Computational Mathematics, 8, pp.21, 2022].
-
Functional Description:
ParaCirce implements a parallel Circulant Embedding method for the generation in parallel of 2D or 3D Gaussian Random Fields (second order stationary).
-
Release Contributions:
- Padding estimation - Use case examples - User documentation
-
News of the Year:
ParaCirce now implements hybrid MPI and OpenMP Parallel Programming.
- URL:
- Publication:
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Simon Legrand
7.1.3 nef-flow-fpm
-
Keywords:
2D, 3D, Porous media, Fracture network, Geophysical flows
-
Scientific Description:
The code is based on the implementation of the mixed hybrid finite element method as detailed in: An efficient numerical model for incompressible two-phase flow in fractured media Hussein Hoteit, Abbas Firoozabadi, Advances in Water Resources 31, 891–905, 2008. https://doi.org/10.1016/j.advwatres.2008.02.004
The model of fractures and the coupling between the porous flow and the flow in the network of fractures is described in: : Modeling Fractures and Barriers as Interfaces for Flow in Porous Media V. Martin, J. Jaffré, J. E. Roberts, SIAM Journal on Scientific Computing, 2005. https://doi.org/10.1137/S1064827503429363
Validation benchmark test from the publication: Inga Berre, et al., Verification benchmarks for single-phase flow in three-dimensional fractured porous media, Advances in Water Resources, Volume 147, 2021. https://doi.org/10.1016/j.advwatres.2020.103759.
-
Functional Description:
nef-flow-fpm is a Matlab code to simulate flows in fractured porous media with the mixed-hybrid finite element methods (RT0).
-
Release Contributions:
Implementation of the mixed hybrid method for 3D porous flows, Discrete fracture Networks (DFN) flows and the coupling between DFN and porous flows.
-
News of the Year:
Comparison of direct versus iterative solvers on fractured porous media of increasing complexity, the largest networks contains 23k fractures.
Add possible call to the linear direct solver MUMPS: https://mumps-solver.org/index.php
- URL:
-
Contact:
Geraldine Pichot
-
Participants:
Geraldine Pichot, Daniel Zegarra Vasquez, Michel Kern
7.1.4 Skwer
-
Keywords:
Differential equations, State-oriented simulation
-
Scientific Description:
Unlike classical approaches which discretize time a priori to determine the state, the State-Oriented Simulation (SOS) method discretizes the state to determine durations, thus following ideas from the Quantized State Systems (QSS) methods. The aim is to give rigorous interpretation of idealized or hybrid physical models, and of cosimulation. The aspect that most distinguishes us from other approaches is that we do not make use of differential-algebraic equations (DAEs). We rather solve more general multiscale numerical stiffness problems based on nonstandard ODE formulations.
-
Functional Description:
Skwer aims at solving differential equations inherent to 0D physical modeling. This includes in particular standard ODEs but also differential equations with conditionals and "idealized behavior" resulting from passing to the limit over some parameters.
-
News of the Year:
We have developed several OCaml modules to handle data structures and functions required to build the Skwer simulator. This includes symbolic manipulation of differential equation terms, generation of Maclaurin series terms, and computations with intervals. These modules are at the heart of the simulation engine which, unlike most popular solvers, heavily relies on information gathered from the syntax of equations through suitable evaluations. These range from incidence graphs to Maclaurin series or interval results from the same equation descriptions as needed by the various algorithms involved in the simulation process.
- URL:
- Publication:
-
Contact:
Sebastien Furic
-
Participants:
Sebastien Furic, François Clement, Geraldine Pichot
7.1.5 coq-num-analysis
-
Name:
Numerical analysis Coq library
-
Keywords:
Coq, Numerical analysis, Real analysis
-
Scientific Description:
These Coq developments are based on the Coquelicot library for real analysis. Version 1.0 includes the formalization and proof of: (1) the Lax-Milgram theorem, including results from linear algebra, geometry, functional analysis and Hilbert spaces, (2) the Lebesgue integral, including large parts of the measure theory,the building of the Lebesgue measure on real numbers, integration of nonnegative measurable functions with the Beppo Levi (monotone convergence) theorem, Fatou's lemma, the Tonelli theorem, and the Bochner integral with the dominated convergence theorem.
-
Functional Description:
Formal developments and proofs in Coq of numerical analysis problems. The current long-term goal is to formally prove parts of a C++ library implementing the Finite Element Method.
-
News of the Year:
Opam package (version 1.0). In progress: formalization of the concept of finite element.
- URL:
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Sylvie Boldo, François Clement, Micaela Mayero, Vincent Martin, Stéphane Aubry, Florian Faissole, Houda Mouhcine, Louise Leclerc
-
Partners:
LIPN (Laboratoire d'Informatique de l'Université Paris Nord), LMAC (Laboratoire de Mathématiques Appliquées de Compiègne)
7.1.6 MODFRAC
-
Name:
MODFRAC
-
Keywords:
Meshing, Fracture network, Ellipses, Polygons, Mesher, Mesh
-
Scientific Description:
The meshing methodology is based on a combined frontal-Delaunay approach in a Riemannian context.
-
Functional Description:
The MODFRAC software automatically builds meshes of fracture networks. As an input, it takes a DFN (Discrete Fracture Network) geometric model consisting of ellipses or polygons that have been randomly generated in the tridimensional space while following experimental statistics. It completes this model by first calculating the intersections between fractures, that are straight segments. On each fracture, it computes in turn the intersections between these straight segments, subdividing them into subsegments. It then creates a conforming set of these subsegments, and selects the necessary fractures using a graph structure. It transmits this information to an “indirect” surface mesher, where the tridimensional mesh results from the construction of planar meshes of the parametric domains.
-
News of the Year:
[New feature] The fracture network can be given as a .geo file where each fracture is defined as a polygon. [New feature] possibilitity to add wells defined in a .geo file [Computational performance] MODFRAC is able to mesh networks with more than 1 million of fractures in less than 12 minutes, with 4 threads on a laptop. [Mesh quality of MODFRAC meshes] Large-scale fracture networks (up to 87k fractures) have been successfully meshed with a volume mesher, based on the MODFRAC mesh
- Publications:
-
Contact:
Geraldine Pichot
-
Participants:
Patrick Laug, Houman Borouchaki, Geraldine Pichot
-
Partner:
Université de Technologie de Troyes
7.1.7 Prune_rs
-
Keywords:
Combinatorics, Parameter studies, Automation
-
Functional Description:
Prune_rs is a language aimed at automating parameter studies. It allows the specification of parameter combinations, and make them available via environment variables. Those can then be used by any specified command as input parameters.
-
Release Contributions:
- Parameter space specification - Launching commands with each combination as parameter - File system interaction with read/write functions and Json format
-
Authors:
Thierry Martinez, Simon Legrand, Geraldine Pichot
-
Contact:
Thierry Martinez
7.1.8 nef-transport-fpm
-
Keywords:
3D, Porous media, Incompressible flows, Transport model
-
Scientific Description:
The discretization in space is performed with a cell-centered finite volume scheme. The discretization in time can be either explicit or implicit.
-
Functional Description:
nef-transport-fpm is a Matlab code for simulating transport by advection diffusion in porous-fractured media.
-
News of the Year:
This first release only deals with pure advective transport in the rock matrix.
-
Contact:
Geraldine Pichot
7.1.9 FEMLAB
-
Name:
FEMLAB
-
Keywords:
High order finite elements, Discontinuous Galerkin, Hybrid high-order methods, Adaptive algorithms, Finite element modelling
-
Functional Description:
FEMLAB is a Matlab library for different classes of FEM code. This library is designed to use a parallel computing toolbox in Matlab to accelerate the time for assembling the linear systems. It has been tested on 48 parallel processors of the HPC nodes. Another critical point is that different FEM codes in this library are designed to support arbitrary order of the basis functions. Another critical point is that different FEM codes in this library are designed to support arbitrary order of the basis functions.
-
Release Contributions:
FEMLAB is now available!
-
News of the Year:
FEMLAB is available from 2022.
- URL:
- Publications:
-
Contact:
Zhaonan Dong
7.1.10 APS-MG
-
Name:
A-Posteriori-Steered MultiGrid
-
Keywords:
Finite element modelling, Linear system, A posteriori error estimates, Multigrid methods, P-robustness
-
Scientific Description:
APS-MG (a-posteriori-steered multigrid) is a geometric-type multigrid solver whose execution is steered by the associated a posteriori estimate of the algebraic error. In particular, the descent direction and the level-wise step sizes are adaptively optimized. APS-MG corresponds to a V-cycle geometric multigrid with zero pre- and solely one post-smoothing step, via block-Jacobi (overlapping additive Schwarz/local patchwise problems). Its particularity is that it is robust with respect to the polynomial degree p of the underlying finite element discretization, i.e., APS-MG contracts the error on each iteration by a factor that is independent of p. APS-MG is the implementation of the solver developed in https://hal.science/hal-02070981 and https://hal.science/hal-02494538.
-
Functional Description:
APS-MG (a-posteriori-steered multigrid) is an iterative linear solver implemented in MATLAB. It can treat systems of linear algebraic equations arising from order p conforming finite element discretization of second-order elliptic diffusion problems. APS-MG is a geometric-type multigrid method and uses a hierarchy of nested meshes. It corresponds to a V-cycle geometric multigrid solver with zero pre- and one post-smoothing step via block-Jacobi (overlapping additive Schwarz/local patchwise problems). A salient feature is the choice of the optimal step size for the descent direction on each mesh level.
- URL:
- Publications:
-
Contact:
Jan Papez
8 New results
8.1 Flow and transport simulation in fractured porous media
Participants: Michel Kern, Dania Khiralla, Géraldine Pichot, Martin Vohralík, Daniel Zegarra Vasquez.
We simulate flow and transport in a network of fractures embedded in an heterogeneous porous medium. The mesh of the fractured network is generated with the software MODFRAC and constraints the volume mesh generator, GHS3D, developed by the Inria GAMMA project-team.
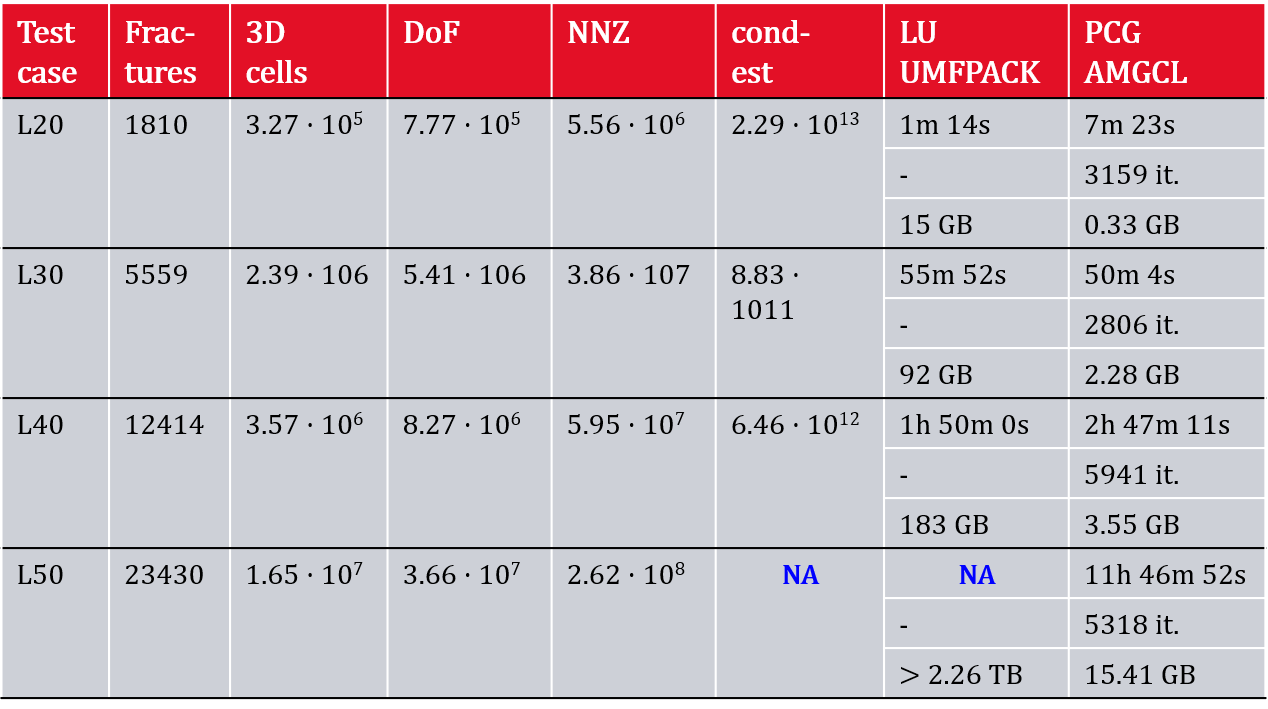
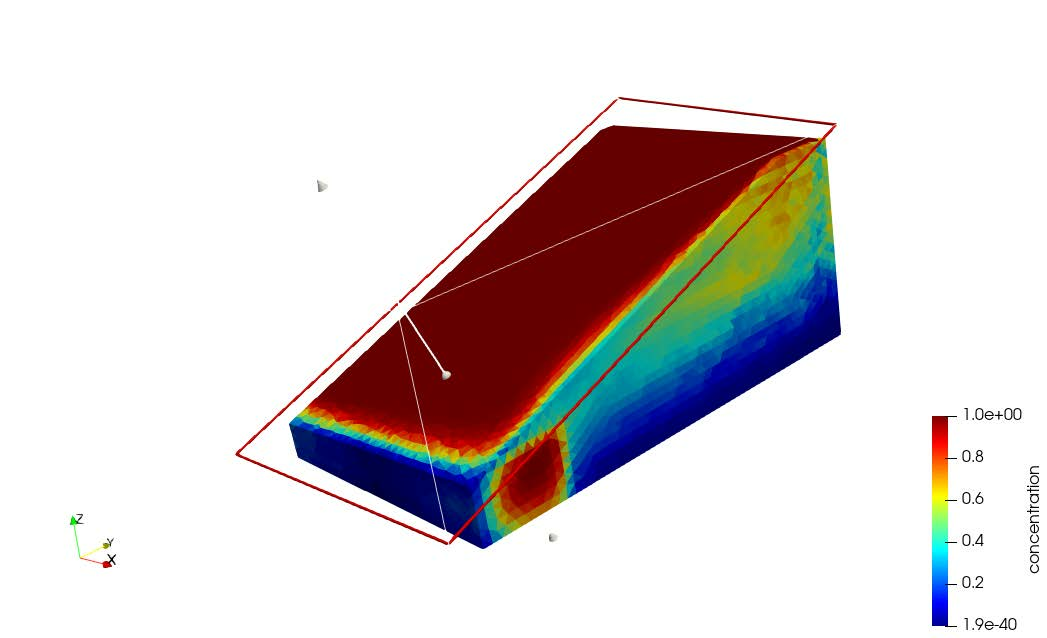
The coupled flow problem between the fractures and the rock matrix is solved with the mixed hybrid finite element method (Raviart-Thomas of lowest order). The method is implemented in the software nef-flow-fpm and has been validated with the established benchmark test case from 49, see Figure 1.
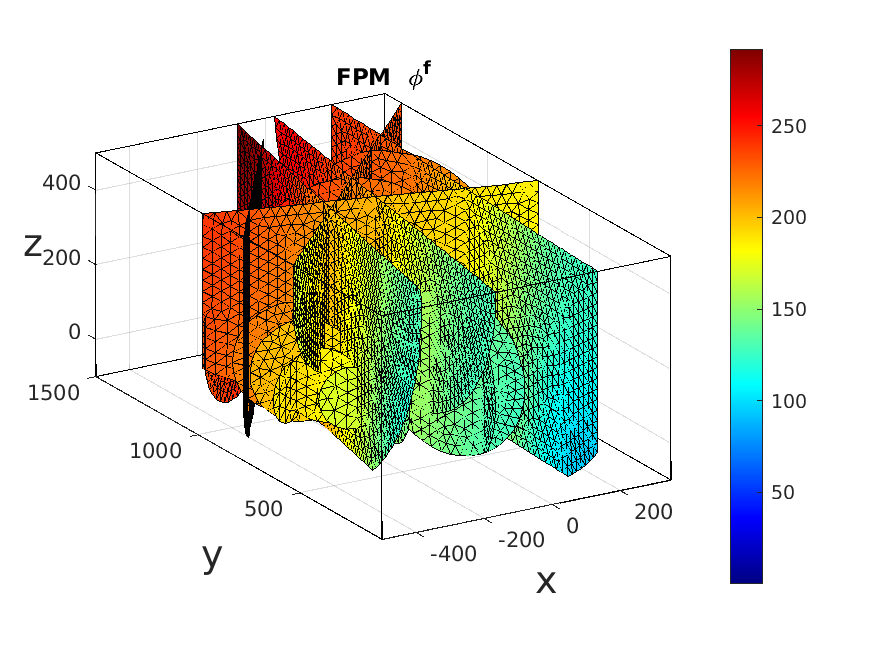
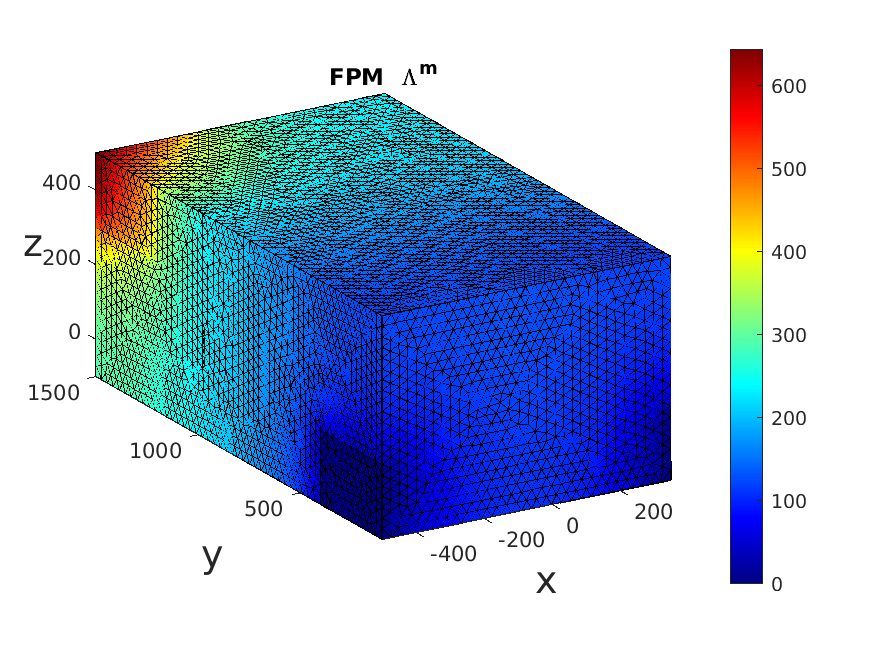
A particularly challenging issue is the solution of the linear system resulting from the discretization: the 3D volume mesh leads to a large number of unknowns, while the fracture network makes the problem very ill conditioned (condition numbers up to have been observed). Direct methods can no longer cope with such large problems, while traditional iterative methods need a very efficient preconditioner to converge. We are able to simulate with nef-flow-fpm flow in a fractured porous medium containing more than 23k fractures and meshed with 16 millions of tetrahedra (see Table 1).
Another goal is to simulate the transport by advection of an inert tracer. The first contribution was to consider a porous medium without the fractures. The transport is described by the conservation of mass and gives rise to an equation with partial derivatives of the first order in which the velocity, computed with the software nef-flow-fpm, is heterogeneous. The discretization in space is performed with a cell-centered finite volume scheme. The discretization in time can be either explicit or implicit. The method is implemented in nef-transport-fpm.
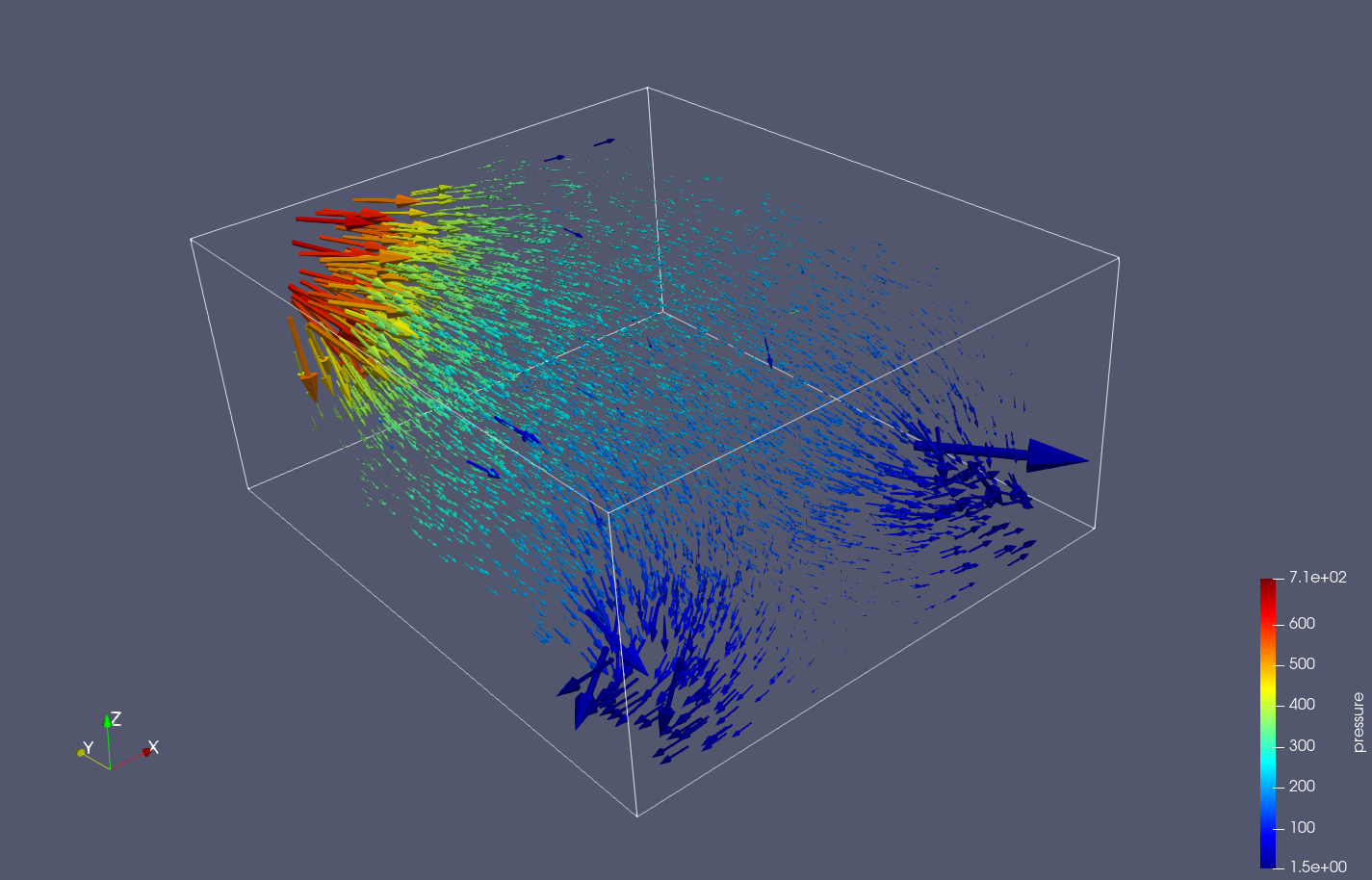
8.2 Parallel generation of Gaussian Random Fields (GRF).
Participants: Géraldine Pichot, Simon Legrand, Michel Kern.
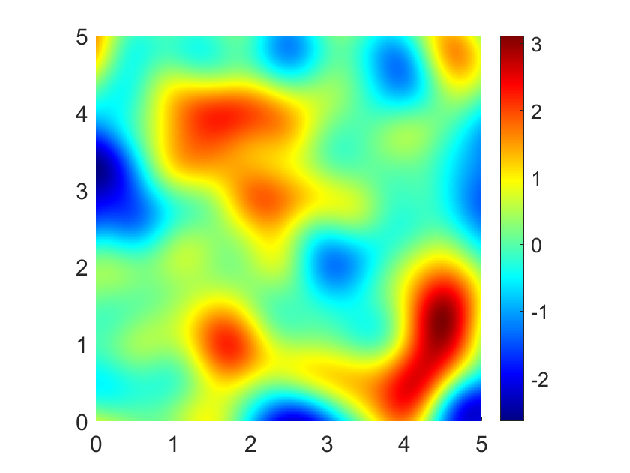
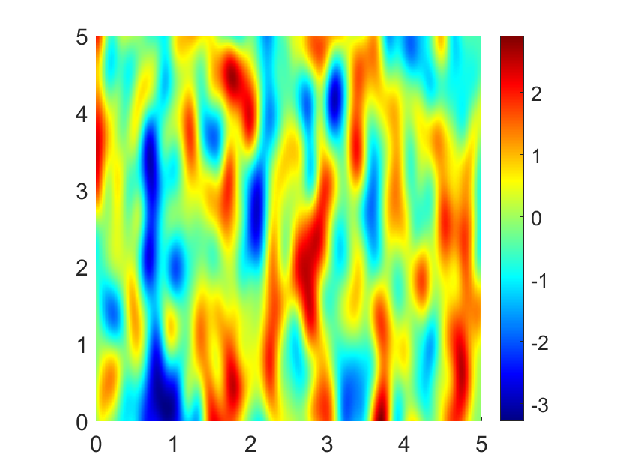
In 31, we have generalized Theorem 2.3 in 51 to the case of rectangular parallelepipeds. Then we have proposed a new initialization stage of the CEM algorithm that makes it possible to quickly jump to a domain size close to the one needed for the CEM algorithm to work. These domain size estimates are based on fitting functions. Examples of fitting functions are given for the Matérn family of covariances. These functions are inspired by our numerical simulations and by the theoretical work from 51. The parameters estimation of the fitting functions is done numerically. Several numerical tests are performed to show the efficiency of the proposed algorithms, for both isotropic and anisotropic Matérn covariances.
Examples of 2D fields with isotropic and anisotropic Gaussian covariances are shown on Figure 3.
8.3 Coq formalizations
Participants: François Clément, Houda Mouhcine.
In 50, we provide detailed proofs for the main results in measure theory and Lebesgue integration theory, to help for their formalization in an interactive theorem prover such as Coq. The document gathers material from several textbooks, but also provides some original views on known concepts such as set systems (e.g. -algebras), numeric functions over set systems (e.g. measures), abstract results about properties satisfied almost everywhere, and the concept of almost sum. Version 2 (April 2021, 700 statements and 200 pages) covered all mathematical aspects of the Coq formalizations presented in 15 and 33 (see below). Version 3 (December 2022, added 450 statements and 130 pages) brings more abstractions, for instance for set systems and numeric functions over set systems (e.g. measures), for properties satisfied almost everywhere, and for simple functions. It also generalizes the chapter on to , up to the Riesz–Fischer theorem.
In 15, we present the Coq formalization of -algebras, measures, simple functions, and integration of nonnegative measurable functions, up to the full formal proofs of the Beppo Levi (monotone convergence) theorem and Fatou's lemma. More than a plain formalization of the known literature, we present several design choices made to balance the harmony between mathematical readability and usability of Coq theorems. These results are a first milestone towards the formalization of spaces as Banach spaces.
In 33, we describe the formal definition and proof in Coq of product -algebras, product measures and their uniqueness, the construction of iterated integrals, up to Tonelli's theorem. We also advertise the Lebesgue induction principle provided by an original inductive type for nonnegative measurable functions.
In 35, we describe the formalization of Bochner integration, a generalization of Lebesgue integration to functions taking their values in a Banach space, up to the dominated convergence theorem. Our contributions include an original formalization of simple functions, Bochner integrability defined by a dependent type, and the proof of the integrability of measurable functions under a weak separability hypothesis.
8.4 Invariant-domain time-stepping
Participants: Alexandre Ern, Jean-Luc Guermond.
In 43, the authors started the development of a novel paradigm laying the foundations of invariant-domain time-stepping for hyperbolic problems using high-order Runge–Kutta methods. Further developments in progress include the extension to implicit-explicit (IMEX) time-stepping and the application to the compressible Navier–Stokes equations.
8.5 Space-time multiscale mortar mixed finite element method for parabolic equations
Participants: Michel Kern, Martin Vohralík.
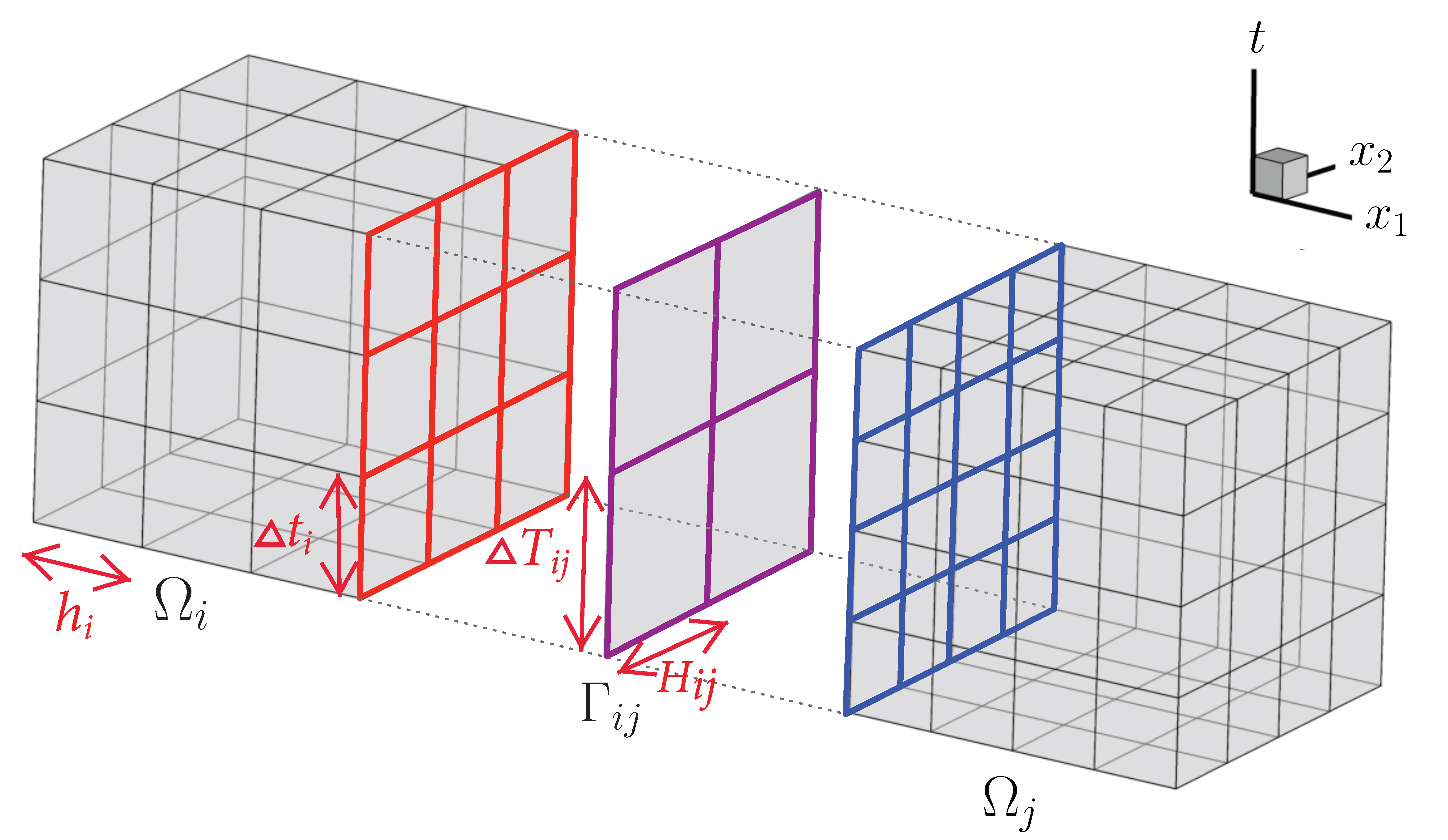
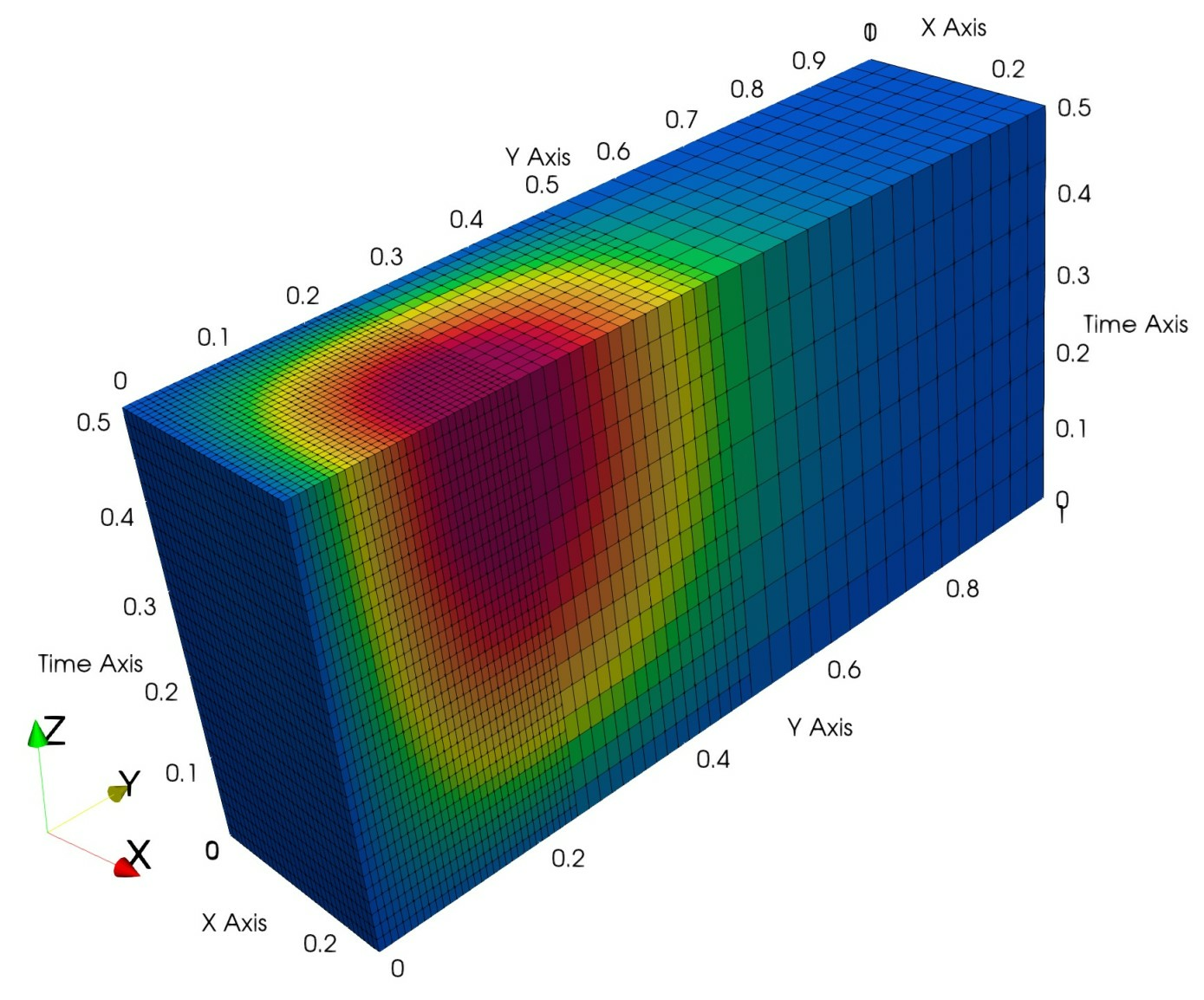
In 28 we develop a space-time mortar mixed finite element method for parabolic problems. The domain is decomposed into a union of subdomains discretized with non-matching spatial grids and asynchronous time steps. The method is based on a space-time variational formulation that couples mixed finite elements in space with discontinuous Galerkin in time. Continuity of flux (mass conservation) across space-time interfaces is imposed via a coarse-scale space-time mortar variable that approximates the primary variable. Uniqueness, existence, and stability, as well as a priori error estimates for the spatial and temporal errors, are established. A space-time non-overlapping domain decomposition method is developed that reduces the global problem to a space-time coarse-scale mortar interface problem. Each interface iteration involves solving in parallel space-time subdomain problems. The spectral properties of the interface operator and the convergence of the interface iteration are analyzed.
Numerical experiments are provided that illustrate the theoretical results and the flexibility of the method for modeling problems with features that are localized in space and time, see Figure 4. This work was in collaboration with I. Yotov and M. Jayadharan.
8.6 Multiscale methods
Participants: Zhaonan Dong.
In 41, the authors proposed a convergence theory for high-order multiscale FEMs independent of the roughness of the diffusion tensor for Poisson problems. We aim to provide a priori and a posteriori error analysis for high-order discontinuous Galerkin multiscale methods for flows problems on heterogeneous domains.
This work was in collaboration with R. Maier and M. Hauck.
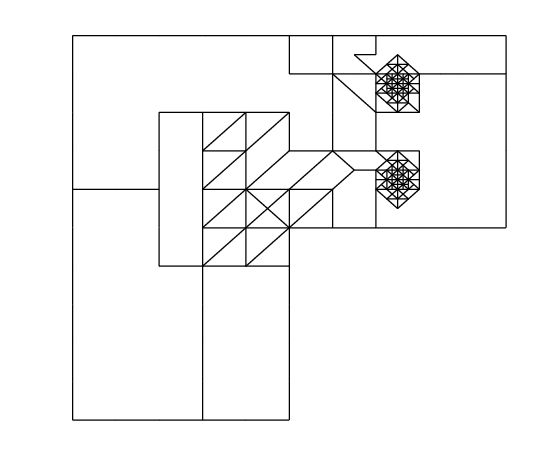
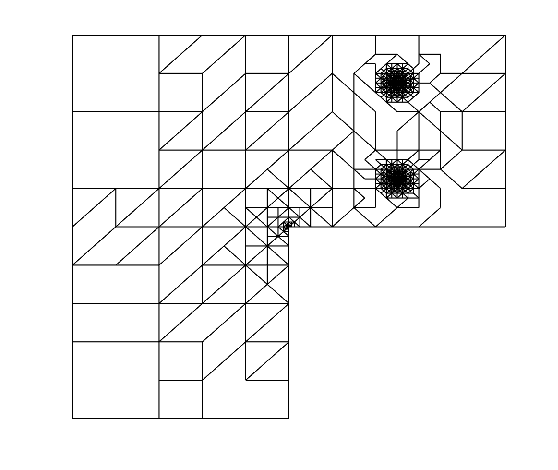
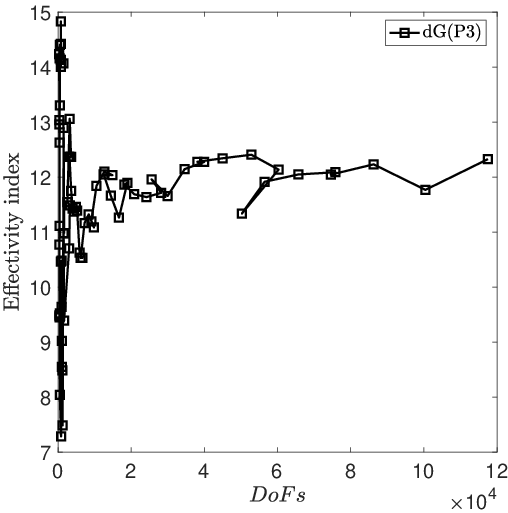
8.7 A posteriori error estimates for discontinuous Galerkin methods on polygonal and polyhedral meshes
Participants: Zhaonan Dong.
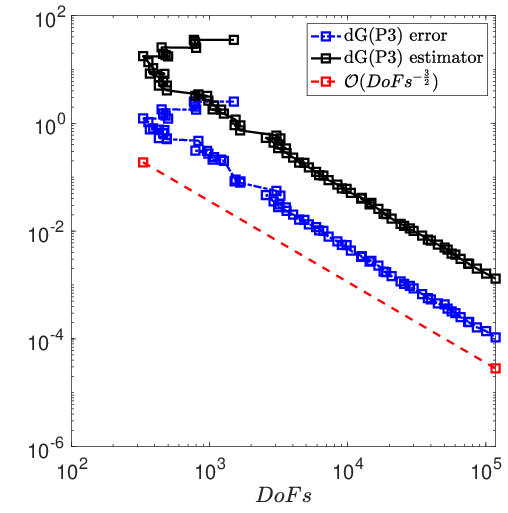
In 38, the authors present a new residual-type energy-norm a posteriori error analysis for interior penalty discontinuous Galerkin (dG) methods for linear elliptic problems. The new error bounds are also applicable to dG methods on meshes consisting of elements with very general polygonal/polyhedral shapes. The case of simplicial and/or box-type elements is included in the analysis as a special case. In particular, for the upper bounds, arbitrary number of very small faces are allowed on each polygonal/polyhedral element, as long as certain mild shape regularity assumptions are satisfied. As a corollary, the present analysis generalizes known a posteriori error bounds for dG methods, allowing in particular for meshes with arbitrary number of irregular hanging nodes per element. The proof hinges on a new conforming recovery strategy in conjunction with a Helmholtz decomposition formula. The resulting a posteriori error bound involves jumps on the tangential derivatives along elemental faces.
Numerical experiments presented in Figure 5 highligts the practical value of the derived a posteriori error bounds as error estimators. This work was performed in collaboration with A. Cangiani and E. H. Georgoulis.
|
|
|
|
|
|
8.8 A posteriori error estimates for the Richards equation
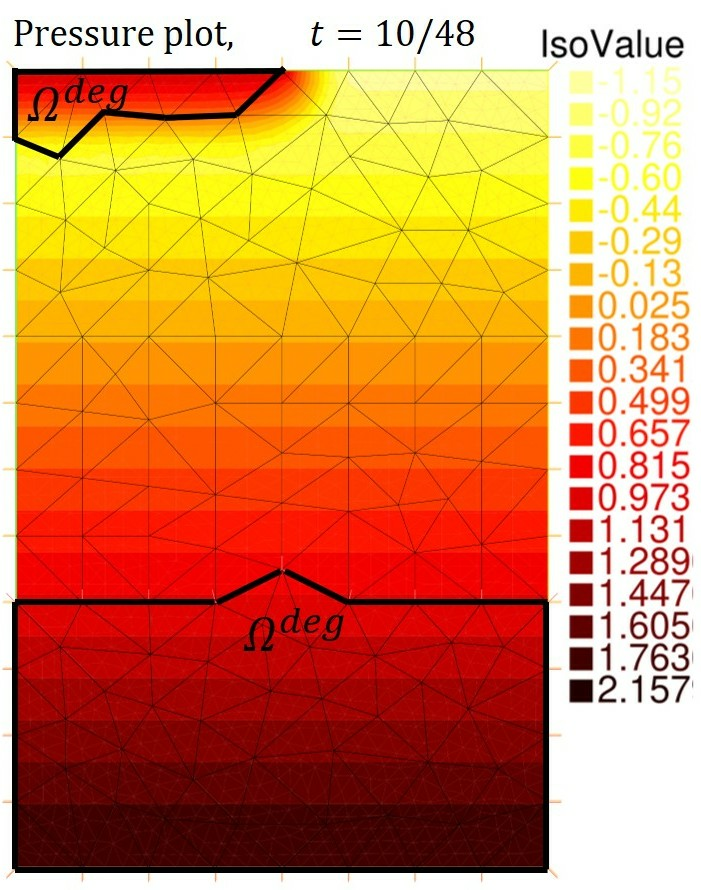
Participants: Martin Vohralík.
In collaboration with K. Mitra, we have in 47 studied the Richards equation. This equation is recognized as principal model for flows in underground porous media. It describes more precisely the flow of water and air through subsoil and serves as a gateway for multiphase flows through porous media. This nonlinear advection–reaction–diffusion equation exhibits both parabolic–hyperbolic and parabolic–elliptic degeneracies, which make its numerical approximation and mathematical analysis very challenging.
In this study, we provide guaranteed, fully computable, and locally space–time efficient a posteriori error bounds for numerical approximations of the doubly-degenerate Richards equation. For showing global reliability, a nonlocal-in-time error estimate is derived individually for the time-integrated , , and the errors. A maximum principle and a degeneracy estimator are employed for the last one. Global and local space–time efficiency error bounds are then obtained in a standard norm. The reliability and efficiency norms employed coincide when there is no nonlinearity. Moreover, error contributors such as flux nonconformity, time discretization, quadrature, linearization, and data oscillation are identified and separated. The estimates are also valid in a setting where iterative linearization with inexact solvers is considered.
Numerical tests are conducted for nondegenerate and degenerate cases having exact solutions, as well as for a realistic/benchmark case. Excellent results are obtained even in this last setting, see Figure 6. The error elementiwse distribution (right) varies here for more than 5 orders of magnitude in the spatial domain at each given time, but it is still correctly predicted by the estimators (middle). The overall space-time estimator only overestimates the error by the factor of 1.05.
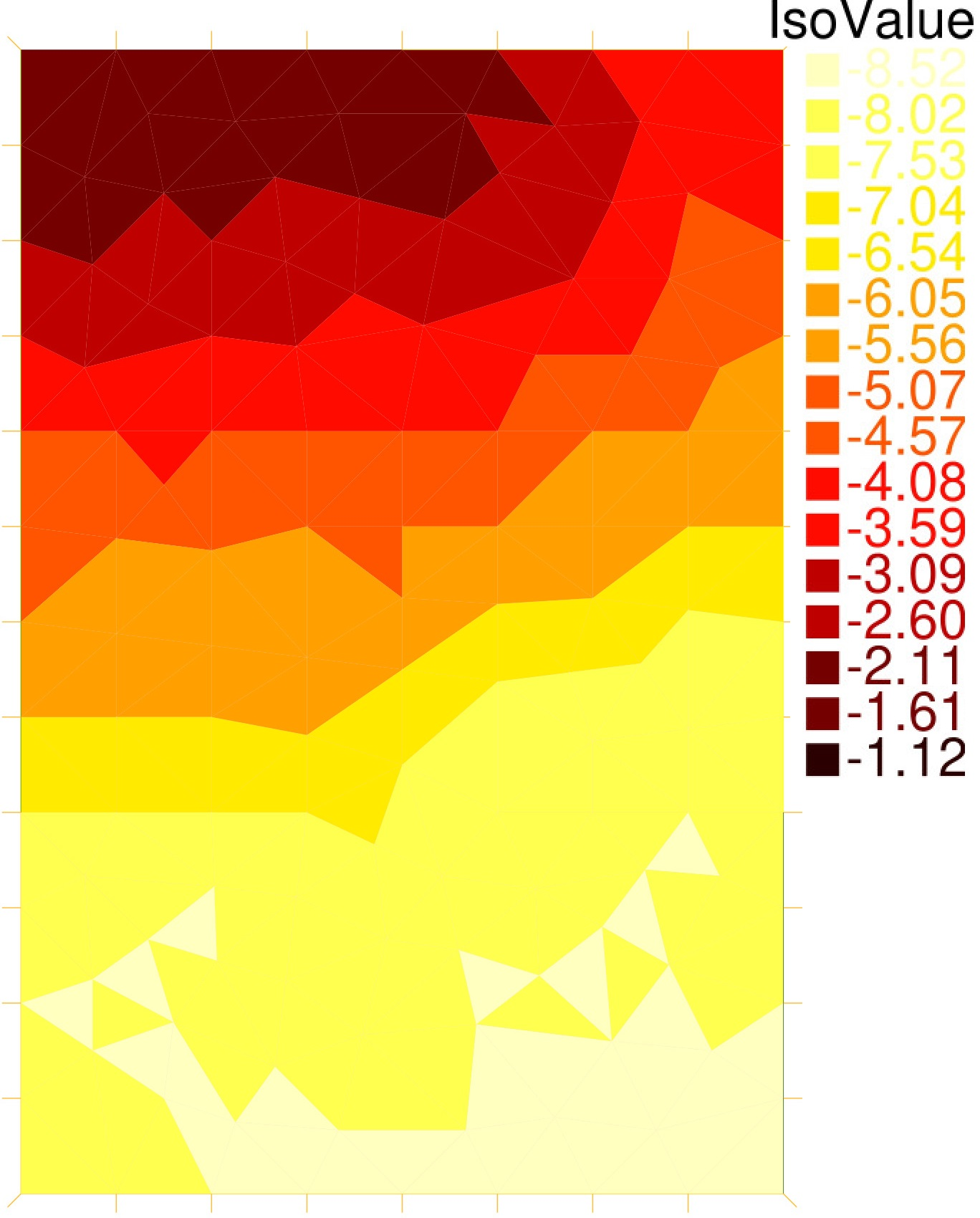
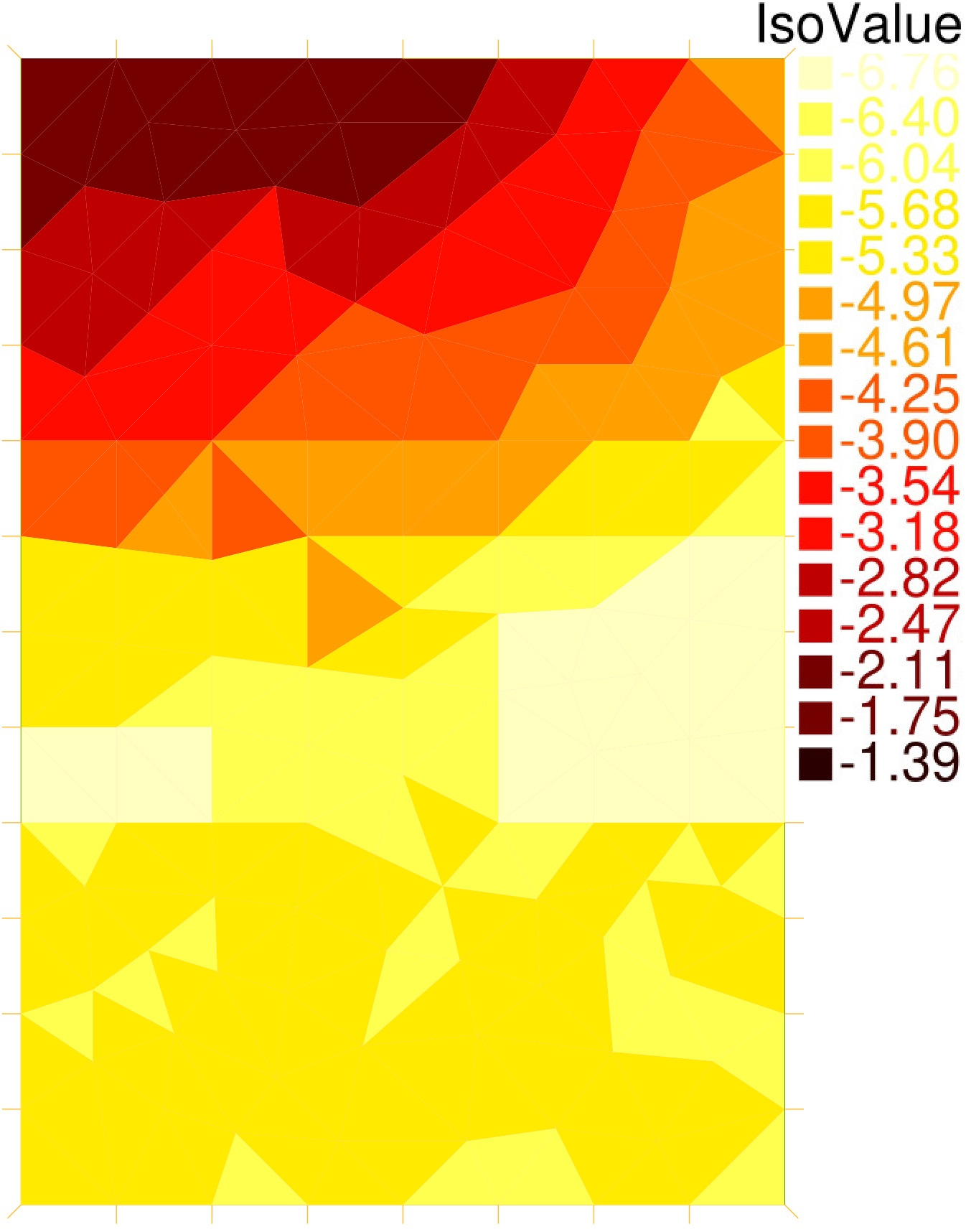
9 Bilateral contracts and grants with industry
9.1 Bilateral contracts with industry
Participants: Alexandre Ern, Martin Vohralík.
- Two-part contract with IFP Energies Nouvelles accompanying the PhD thesis of Joëlle Ferzly.
- Two-part contract with CEA accompanying the PhD thesis of Romain Mottier.
- Two-part contract with EDF accompanying the PhD thesis of Idrissa Niakh.
- Two-part contract with ANDRA accompanying the PhD thesis of Ari Rappaport.
- Two-part contract with CEA accompanying the PhD thesis of Morgane Steins.
10 Partnerships and cooperations
Participants: Zhaonan Dong, Alexandre Ern, Géraldine Pichot, Martin Vohralík.
10.1 International research visitors
10.1.1 Visits of international scientists
Prof. Johnny Guzmán (Brown University, USA) visited the team for two weeks in October 2022. He gave a seminar at the Scientific computing, modeling, and numerical analysis seminar “Rencontres Inria-LJLL en calcul scientifique” (common to Sorbonne University and Inria) and interacted with Alexandre Ern and Martin Vohralík on two topics: (i) local- and global-best approximations in H(div); (ii) localized stability estimates for convective problems without diffusion.
Inria International Chair
Prof. Jean-Luc Guermond (Texas A&M University) visited the team for about two months in 2022. He mainly interacted with Alexandre Ern on invariant-domain time-stepping methods, but he also interacted with Zhaonan Dong on local interpolation estimates in H(curl) and H(div) 23. He also gave a seminar at the working group of the team.
Other international visits to the team
Fabio Vicini
-
Status:
researcher
- Institution of origin:
-
Country:
Italy
-
Dates:
07/11/2022 to 09/12/2022 (1 month)
-
Context of the visit:
Fabio Vicini works in the GEOSCORE group of Politecnico di Torino. GEOSCORE and Serena have a common research topic on the development of efficient and robust numerical methods to solve large-scale subsurface flows with fractures. To this end, during the past years, our respective teams have developed different meshing and numerical strategies. The aim of the stay of Fabio in our team would be to compare these different approaches: matching vs non-matching meshes, Virtual Element Method vs Hybrid High Order method, direct vs iterative solvers, adaptive mesh refinement strategies based on a posteriori error estimates.
-
Mobility program/type of mobility:
research stay
10.2 European initiatives
10.2.1 H2020 projects
EMC2
EMC2 project (or on CORDIS)
-
Title:
Extreme-scale Mathematically-based Computational Chemistry
-
Duration:
From September 1, 2019 to February 28, 2026
-
Partners:
- Inria, France
- ECOLE NATIONALE DES PONTS ET CHAUSSEES (ENPC), France
- CENTRE NATIONAL DE LA RECHERCHE SCIENTIFIQUE CNRS (CNRS), France
- SORBONNE UNIVERSITE, France
-
Inria contact:
Laura GRIGORI (Alpines)
-
Coordinator:
E. Cancès, L. Grigori, Y.Maday, J.-P. Piquemal
-
Summary:
The goal of this ERC Synergy is to develop physical and chemical models in chemistry, condensed matter physics, molecular biology, materials science, and nanosciences, altogether with mathematically-certified and numerically-efficient algorithms, and to implement them in a scalable way on various computer architectures.
11 Dissemination
Participants: Alexandre Ern, Michel Kern, Géraldine Pichot, Martin Vohralík.
11.1 Promoting scientific activities
11.1.1 Scientific events: organisation
Member of the organizing committees
Zhaonan Dong, Alexandre Ern, André Harnist, Ani Miraçi, Ari Rappaport, and Martin Vohralík (also with Jan Papež from the Czech Academy of Sciences in Prague) co-organized the 2022 workshop concluding the ERC consolidator grant GATIPOR.
Alexandre Ern is a member of the Scientific Committee of the European Finite Element Fair.
Michel Kern was a co-organizer of the minisymposium “Mathematical and numerical methods for multi-scale multi-physics, nonlinear coupled processes” at the Interpore 2022 conference.
Martin Vohralík (with Guillaume Enchéry and Ibtihel Ben Gharbia, IFP Energies Nouvelles) organized the regular 1-day workshop Journée contrat cadre IFP Energies Nouvelles – Inria.
Martin Vohralík co-organized, with Mickaël Abbas (EDF R&D), Ludovic Chamoin (ENS Paris-Saclay), and Erell Jamelot, François Madiot, and Pascal Omnes (all CEA Saclay), the CEA-EdF-Inria Summer School on Certification of errors in numerical simulations, held from 27 June to 01 July 2022 at EDF Lab, Paris-Saclay.
11.1.2 Scientific events: selection
Member of the conference program committees
- Géraldine Pichot: Scientific Committee of FRAME2020+2 - FRActured MEdia: Numerical methods for fluid flow and mechanics, May 17-20, 2022, Politecnico di Torino, Italy.
Reviewer
- François Clément served as reviewer for ITP22.
11.1.3 Journal
Member of the editorial boards
Alexandre Ern is a member of the Editorial Board of SIAM Journal on Scientific Computing, ESAIM Mathematical Modelling and Numerical Analysis, IMA Journal of Numerical Analysis, Journal of Scientific Computing, and Computational Methods in Applied Mathematics.
Martin Vohralík is a member of the editorial boards of Acta Polytechnica and Applications of Mathematics.
Reviewer - reviewing activities
Zhaonan Dong was a reviewer for the SIAM Journal on Numerical Analysis, SIAM Journal on Scientific Computing, and Mathematics of Computation.
Alexandre Ern and Martin Vohralík reviewed numerous papers for the leading journals of the field.
Michel Kern reviewed papers for Mathematics and Computers in Similation, Hydrology and Earth System Science, and Computer Methods in Applied Mathematics.
Géraldine Pichot served as reviewer for Engineering Geology.
11.1.4 Invited talks
Alexandre Ern gave a plenary lecture at the POEMS 2022 conference in Milano (December 2022). He also gave an invited talk at the One-World Numerical Analysis seminar.
Michel Kern gave a seminar in the PIMENT team at the Université de la Réunion (December 2022).
Martin Vohralík gave an invited talk at the 34th seminar on Numerical fluid mechanics (January 2022), a keynote talk at Equadiff 15, Brno, Czech Republic (July 2022), and an invited talk at the Singular Days, Nice, France (November 2022).
11.1.5 Leadership within the scientific community
- Alexandre Ern serves at the Administration Board of SMAI and its Executive Committee as Vice-President in charge of relations with the industry.
- Michel Kern is the chair of the Comission de Développement Technologique of the Inria Paris Center.
- Martin Vohralík is the president of the scientific committee of Summer schools CEA–EDF–INRIA.
- Martin Vohralík is a member of the scientific board of the IFP Energies Nouvelles – Inria joint strategic partnership laboratory.
11.1.6 Scientific expertise
Michel Kern is a reviewer for the Allocation of Computing Time located at the Juelich Supercomputing Centre in Germany.
11.1.7 Research administration
- François Clément is a member of the Comité local d'hygiène, de sécurité et des conditions de travail (CLHSCT) of the Inria Paris Centre.
- François Clément is a member of the Commission des usagers de la rue Barrault (CURB) for the next relocation of the Inria Paris Centre.
- Géraldine Pichot is the president of the Commission des utilisateurs des moyens informatiques (CUMI) from January, 2022.
- Michel Kern is a member of the Scientific Board of ORAP, Organisation Associative du Parallélisme.
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- Licence : Alexandre Ern, Numerical analysis, 77h, L3/M1, Ecole Polytechnique, France.
- Master : Alexandre Ern, Discontinuous Galerkin methods, 20h, M2, Sorbonne University, France.
- Graduate course: Alexandre Ern, Hybrid high-order methods, 3h, Hasselt University, Belgium.
- Graduate course: Alexandre Ern, Error certification by a posteriori error estimates, 5h, CEA-EdF-Inria Summer School, Paris Saclay.
- Master: Michel Kern, Models and numerical methods for subsurface flow, 30h, M2, Université Paris Saclay, France.
- Master: Michel Kern, Advanced numerical analysis, 30h, M1, Institut Galilée, Université Paris-Nord, France.
- Master: Martin Vohralík, Advanced finite elements, 21h, M1, ENSTA (Ecole nationale supérieure de techniques avancées), Paris, France.
- Master: Martin Vohralík, A posteriori error estimates for efficiency and error control in numerical simulations, 36h, M2, Charles University, Prague, Czech Republic.
11.2.2 Supervision
- Intership: Dania Khiralla (Sup-Galilée), April to September 2022, Simulation of advective transport in fractured porous media, Michel Kern, Daniel Zegarra Vasquez, and Géraldine Pichot.
- PhD defended: Joëlle Ferzly, Adaptive inexact smoothing Newton method for nonlinear systems with complementarity constraints. Application to a compositional multiphase flow in porous media, November 2019 – October 2022, Martin Vohralík.
- PhD defended: Idrissa Niakh, Reduced-order models for contact and friction problems in mechanics, defended on 14 December 2022, Alexandre Ern.
- PhD in progress: Abbas Kabalan, Model order reduction for nonparametrized geometrical variability, started in fall 2022, Alexandre Ern.
- PhD in progress: Romain Mottier, Unfitted methods for geophysical wave propagation, started in fall 2021, Alexandre Ern.
- PhD in progress: Houda Mouhcine, Formal proofs in applied mathematics: verification of a generator for quadrature formulas, started 1st October 2021, Sylvie Boldo (Toccata), François Clément, Micaela Mayero (LIPN).
- PhD in progress: Stefano Piccardo, Interface problems between immiscible Stokes flows, started in fall 2019, the second half taking place at UPC Barcelona, Alexandre Ern.
- PhD in progress: Ari Rappaport, Adaptivity of model, linear and nonlinear solvers, and local conservation by post-processing. Application to transport problems in underground repositories, started 01 January 2021, Martin Vohralík.
- PhD in progress: Morgane Steins, Hybrid high-order methods for wave propagation, started in fall 2020, Alexandre Ern and Martin Vohralík.
- PhD in progress: Zuodong Wang, Finite element methods for hyperbolic and degenerate parabolic problems, started 01 October 2022, Zhaonan Dong and Alexandre Ern.
- PhD in progress: Daniel Zegarra Vasquez, High-performance simulation of single-phase flows in a fractured porous medium, started 01 October 2021, Michel Kern, Géraldine Pichot, and Martin Vohralík.
11.2.3 Juries
- Alexandre Ern was external reviewer for the HDR of Sébastien Imperiale (Inria Saclay), the PhD thesis of Simon Beck (University of Dresden) and the PhD thesis of Ludovico Bruni (University of Trento).
- Michel Kern was a member of the PhD thesis committee of Grégory Étangsale, defended on December 8th at Université de la Réunion.
- Martin Vohralík was a referee for the PhD thesis of Raphaël Bulle (University of Luxembourg) and Ondine Chanon (EPFL Lausanne).
11.3 Popularization
11.3.1 Internal or external Inria responsibilities
- Géraldine Pichot was a member of the editorial committee of Interstices until February, 2022.
12 Scientific production
12.1 Major publications
- 1 articleA posteriori error estimates and stopping criteria for space-time domain decomposition for two-phase flow between different rock types.SMAI Journal of Computational Mathematics5December 2019, 195-227
- 2 inproceedingsA Coq formal proof of the Lax–Milgram theorem.6th ACM SIGPLAN Conference on Certified Programs and ProofsParis, FranceJanuary 2017
- 3 articleTrusting computations: A mechanized proof from partial differential equations to actual program.Computers and Mathematics with Applications683August 2014, 325--352
- 4 articleGuaranteed and robust a posteriori bounds for Laplace eigenvalues and eigenvectors: conforming approximations.SIAM Journal on Numerical Analysis555September 2017, 2228-2254
-
5
article
-Version discontinuous Galerkin methods on essentially arbitrarily-shaped elements.Mathematics of Computation91333January 2022, 1-35 - 6 articleA hybrid high-order locking-free method for linear elasticity on general meshes.Comput. Methods Appl. Mech. Engrg.2832015, 1--21URL: http://dx.doi.org/10.1016/j.cma.2014.09.009
-
7
articleEquivalence of local-and global-best approximations, a simple stable local commuting projector, and optimal
approximation estimates in (div).IMA Journal of Numerical Analysis422April 2022, 1023-1049 - 8 articleFinite element quasi-interpolation and best approximation.ESAIM Math. Model. Numer. Anal.5142017, 1367--1385URL: https://doi.org/10.1051/m2an/2016066
- 9 miscHybrid high-order methods for flow simulations in extremely large discrete fracture networks.November 2022
- 10 articlePolynomial-degree-robust a posteriori estimates in a unified setting for conforming, nonconforming, discontinuous Galerkin, and mixed discretizations.SIAM Journal on Numerical Analysis532April 2015, 1058-1081
- 11 articleStable broken H1 and H(div) polynomial extensions for polynomial-degree-robust potential and flux reconstruction in three space dimensions.Mathematics of Computation89322March 2020, 551-594
- 12 articleSpace-time domain decomposition methods for diffusion problems in mixed formulations.SIAM J. Numer. Anal.5162013, 3532--3559URL: http://dx.doi.org/10.1137/130914401
12.2 Publications of the year
International journals
International peer-reviewed conferences
Conferences without proceedings
Doctoral dissertations and habilitation theses
Reports & preprints
12.3 Cited publications
- 49 articleVerification benchmarks for single-phase flow in three-dimensional fractured porous media..Advances in Water Resources147103759URL: https://www.sciencedirect.com/science/article/pii/S0309170820301603
- 50 techreportLebesgue integration. Detailed proofs to be formalized in Coq.RR-9386Version 3 is a major revision of the document (see Foreword).Inria ParisJanuary 2021, 567
- 51 articleAnalysis of Circulant Embedding Methods for Sampling Stationary Random Fields.SIAM Journal on Numerical Analysis563January 2018, 1871--1895URL: https://epubs.siam.org/doi/abs/10.1137/17M1149730