2023Activity reportProject-TeamSIROCCO
RNSR: 201221227A- Research center Inria Centre at Rennes University
- Team name: Analysis representation, compression and communication of visual data
- In collaboration with:Institut de recherche en informatique et systèmes aléatoires (IRISA)
- Domain:Perception, Cognition and Interaction
- Theme:Vision, perception and multimedia interpretation
Keywords
Computer Science and Digital Science
- A5. Interaction, multimedia and robotics
- A5.3. Image processing and analysis
- A5.4. Computer vision
- A5.9. Signal processing
- A9. Artificial intelligence
Other Research Topics and Application Domains
- B6. IT and telecom
1 Team members, visitors, external collaborators
Research Scientists
- Christine Guillemot [Team leader, INRIA, Senior Researcher, HDR]
- Thomas Maugey [INRIA, Senior Researcher, from Oct 2023, HDR]
- Aline Roumy [INRIA, Senior Researcher, HDR]
Post-Doctoral Fellow
- Rémy Leroy [INRIA, Post-Doctoral Fellow, from May 2023]
PhD Students
- Ipek Anil Atalay Appak [CEA]
- Denis Bacchus [INRIA]
- Tom Bachard [UNIV RENNES I]
- Stephane Belemkoabga [TYNDAL FX, CIFRE, from Oct 2023]
- Tom Bordin [INRIA]
- Nicolas Charpenay [UNIV RENNES]
- Davi Rabbouni De Carvalho Freitas [INRIA]
- Rita Fermanian [INRIA]
- Kai Gu [INRIA]
- Reda Kaafarani [MEDIAKIND]
- Brandon Le Bon [INRIA]
- Arthur Lecert [INRIA]
- Yiqun Liu [ATEME (Cifre)]
- Esteban Pesnel [MEDIAKIND, from Nov 2023]
- Claude Petit [INRIA]
- Rémi Piau [INRIA]
- Soheib Takhtardeshir [UNIV MID SWEDEN]
- Samuel Willingham [INRIA]
Technical Staff
- Sébastien Bellenous [INRIA, Engineer]
Interns and Apprentices
- Antonin Joly [INRIA]
Administrative Assistant
- Caroline Tanguy [INRIA]
External Collaborator
- Nicolas Keriven [CNRS]
2 Overall objectives
2.1 Introduction
Efficient processing, i.e., analysis, storage, access and transmission of visual content, with continuously increasing data rates, in environments which are more and more mobile and distributed, remains a key challenge of the signal and image processing community. New imaging modalities, High Dynamic Range (HDR) imaging, multiview, plenoptic, light fields, 360o videos, generating very large volumes of data contribute to the sustained need for efficient algorithms for a variety of processing tasks.
Building upon a strong background on signal/image/video processing and information theory, the goal of the SIROCCO team is to design mathematically founded tools and algorithms for visual data analysis, modeling, representation, coding, and processing, with for the latter area an emphasis on inverse problems related to super-resolution, view synthesis, HDR recovery from multiple exposures, denoising and inpainting. Even if 2D imaging is still within our scope, the goal is to give a particular attention to HDR imaging, light fields, and 360o videos. The project-team activities are structured and organized around the following inter-dependent research axes:
- Visual data analysis
- Signal processing and learning methods for visual data representation and compression
- Algorithms for inverse problems in visual data processing
- User-centric compression.
While aiming at generic approaches, some of the solutions developed are applied to practical problems in partnership with industry (InterDigital, Ateme, Orange) or in the framework of national projects. The application domains addressed by the project are networked visual applications taking into account their various requirements and needs in terms of compression, of network adaptation, of advanced functionalities such as navigation, interactive streaming and high quality rendering.
2.2 Visual Data Analysis
Most visual data processing problems require a prior step of data analysis, of discovery and modeling of correlation structures. This is a pre-requisite for the design of dimensionality reduction methods, of compact representations and of fast processing techniques. These correlation structures often depend on the scene and on the acquisition system. Scene analysis and modeling from the data at hand is hence also part of our activities. To give examples, scene depth and scene flow estimation is a cornerstone of many approaches in multi-view and light field processing. The information on scene geometry helps constructing representations of reduced dimension for efficient (e.g. in interactive time) processing of new imaging modalities (e.g. light fields or 360o videos).
2.3 Signal processing and learning methods for visual data representation and compression
Dimensionality reduction has been at the core of signal and image processing methods, for a number of years now, hence have obviously always been central to the research of SIROCCO. These methods encompass sparse and low-rank models, random low-dimensional projections in a compressive sensing framework, and graphs as a way of representing data dependencies and defining the support for learning and applying signal de-correlating transforms. The study of these models and signal processing tools is even more compelling for designing efficient algorithms for processing the large volumes of high-dimensionality data produced by novel imaging modalities. The models need to be adapted to the data at hand through learning of dictionaries or of neural networks. In order to define and learn local low-dimensional or sparse models, it is necessay to capture and understand the underlying data geometry, e.g. with the help of manifolds and manifold clustering tools. It also requires exploiting the scene geometry with the help of disparity or depth maps, or its variations in time via coarse or dense scene flows.
2.4 Algorithms for inverse problems in visual data processing
Based on the above models, besides compression, our goal is also to develop algorithms for solving a number of inverse problems in computer vision. Our emphasis is on methods to cope with limitations of sensors (e.g. enhancing spatial, angular or temporal resolution of captured data, or noise removal), to synthesize virtual views or to reconstruct (e.g. in a compressive sensing framework) light fields from a sparse set of input views, to recover HDR visual content from multiple exposures, and to enable content editing (we focus on color transfer, re-colorization, object removal and inpainting). Note that view synthesis is a key component of multiview and light field compression. View synthesis is also needed to support user navigation and interactive streaming. It is also needed to avoid angular aliasing in some post-capture processing tasks, such as re-focusing, from a sparse light field. Learning models for the data at hand is key for solving the above problems.
2.5 User-centric compression
The ever-growing volume of image/video traffic motivates the search for new coding solutions suitable for band and energy limited networks but also space and energy limited storage devices. In particular, we investigate compression strategies that are adapted to the users needs and data access requests in order to meet all these transmission and/or storage constraints. Our first goal is to address theoretical issues such as the information theoretical bounds of these compression problems. This includes compression of a database with random access, compression with interactivity, and also data repurposing that takes into account the users needs and user data perception. A second goal is to construct practical coding for all these problems.
3 Research program
3.1 Introduction
The research activities on analysis, compression and communication of visual data mostly rely on tools and formalisms from the areas of statistical image modeling, of signal processing, of machine learning, of coding and information theory. Some of the proposed research axes are also based on scientific foundations of computer vision (e.g. multi-view modeling and coding). We have limited this section to some tools which are central to the proposed research axes, but the design of complete compression and communication solutions obviously rely on a large number of other results in the areas of motion analysis, transform design, entropy code design, etc which cannot be all described here.
3.2 Data Dimensionality Reduction
Keywords: Manifolds, graph-based transforms, compressive sensing.
Dimensionality reduction encompasses a variety of methods for low-dimensional data embedding, such as sparse and low-rank models, random low-dimensional projections in a compressive sensing framework, and sparsifying transforms including graph-based transforms. These methods are the cornerstones of many visual data processing tasks (compression, inverse problems).
Sparse representations, compressive sensing, and dictionary learning have been shown to be powerful tools for efficient processing of visual data. The objective of sparse representations is to find a sparse approximation of a given input data. In theory, given a dictionary matrix , and a data with and is of full row rank, one seeks the solution of where denotes the norm of , i.e. the number of non-zero components in . is known as the dictionary, its columns are the atoms, they are assumed to be normalized in Euclidean norm. There exist many solutions to . The problem is to find the sparsest solution , i.e. the one having the fewest nonzero components. In practice, one actually seeks an approximate and thus even sparser solution which satisfies for some , characterizing an admissible reconstruction error.
The recent theory of compressed sensing, in the context of discrete signals, can be seen as an effective dimensionality reduction technique. The idea behind compressive sensing is that a signal can be accurately recovered from a small number of linear measurements, at a rate much smaller than what is commonly prescribed by the Shannon-Nyquist theorem, provided that it is sparse or compressible in a known basis. Compressed sensing has emerged as a powerful framework for signal acquisition and sensor design, with a number of open issues such as learning the basis in which the signal is sparse, with the help of dictionary learning methods, or the design and optimization of the sensing matrix. The problem is in particular investigated in the context of light fields acquisition, aiming at novel camera design with the goal of offering a good trade-off between spatial and angular resolution.
While most image and video processing methods have been developed for cartesian sampling grids, new imaging modalities (e.g. point clouds, light fields) call for representations on irregular supports that can be well represented by graphs. Reducing the dimensionality of such signals require designing novel transforms yielding compact signal representation. One example of transform is the Graph Fourier transform whose basis functions are given by the eigenvectors of the graph Laplacian matrix , where is a diagonal degree matrix whose diagonal element is equal to the sum of the weights of all edges incident to the node , and the adjacency matrix. The eigenvectors of the Laplacian of the graph, also called Laplacian eigenbases, are analogous to the Fourier bases in the Euclidean domain and allow representing the signal residing on the graph as a linear combination of eigenfunctions akin to Fourier Analysis. This transform is particularly efficient for compacting smooth signals on the graph. The problems which therefore need to be addressed are (i) to define graph structures on which the corresponding signals are smooth for different imaging modalities and (ii) the design of transforms compacting well the signal energy with a tractable computational complexity.
—————————————
3.3 Deep neural networks
Keywords: Autoencoders, Neural Networks, Recurrent Neural Networks.
From dictionary learning which we have investigated a lot in the past, our activity is now evolving towards deep learning techniques which we are considering for dimensionality reduction. We address the problem of unsupervised learning of transforms and prediction operators that would be optimal in terms of energy compaction, considering autoencoders and neural network architectures.
An autoencoder is a neural network with an encoder , parametrized by , that computes a representation from the data , and a decoder , parametrized by , that gives a reconstruction of . Autoencoders can be used for dimensionality reduction, compression, denoising. When it is used for compression, the representation needs to be quantized, leading to a quantized representation . If an autoencoder has fully-connected layers, the architecture, and the number of parameters to be learned, depends on the image size. Hence one autoencoder has to be trained per image size, which poses problems in terms of genericity.
To avoid this limitation, architectures without fully-connected layer and comprising instead convolutional layers and non-linear operators, forming convolutional neural networks (CNN) may be preferrable. The obtained representation is thus a set of so-called feature maps.
The other problems that we address with the help of neural networks are scene geometry and scene flow estimation, view synthesis, prediction and interpolation with various imaging modalities. The problems are posed either as supervised or unsupervised learning tasks. Our scope of investigation includes autoencoders, convolutional networks, variational autoencoders and generative adversarial networks (GANs) but also recurrent networks and in particular Long Short Term Memory (LSTM) networks. Recurrent neural networks attempting to model time or sequence dependent behaviour, by feeding back the output of a neural network layer at time t to the input of the same network layer at time t+1, have been shown to be interesting tools for temporal frame prediction. LSTMs are particular cases of recurrent networks made of cells composed of three types of neural layers called gates.
Deep neural networks have also been shown to be very promising for solving inverse problems (e.g. super-resolution, sparse recovery in a compressive sensing framework, inpainting) in image processing. Variational autoencoders, GANs, learn, from a set of examples, the latent space or the manifold in which the images, that we search to recover, reside. The inverse problems can be re-formulated using a regularization in the latent space learned by the network. For the needs of the regularization, the learned latent space may need to verify certain properties such as preserving distances or neighborhood of the input space, or in terms of statistical modeling. GANs, trained to produce images that are plausible, are also useful tools for learning texture models, expressed via the filters of the network, that can be used for solving problems like inpainting or view synthesis.
—————————————
3.4 Coding theory
Keywords: OPTA limit (Optimum Performance Theoretically Attainable), Rate allocation, Rate-Distortion optimization, lossy coding, joint source-channel coding multiple description coding, channel modelization, oversampled frame expansions, error correcting codes..
Source coding and channel coding theory 1 is central to our compression and communication activities, in particular to the design of entropy codes and of error correcting codes. Another field in coding theory which has emerged in the context of sensor networks is Distributed Source Coding (DSC). It refers to the compression of correlated signals captured by different sensors which do not communicate between themselves. All the signals captured are compressed independently and transmitted to a central base station which has the capability to decode them jointly. DSC finds its foundation in the seminal Slepian-Wolf 2 (SW) and Wyner-Ziv 3 (WZ) theorems. Let us consider two binary correlated sources and . If the two coders communicate, it is well known from Shannon's theory that the minimum lossless rate for and is given by the joint entropy . Slepian and Wolf have established in 1973 that this lossless compression rate bound can be approached with a vanishing error probability for long sequences, even if the two sources are coded separately, provided that they are decoded jointly and that their correlation is known to both the encoder and the decoder.
In 1976, Wyner and Ziv considered the problem of coding of two correlated sources and , with respect to a fidelity criterion. They have established the rate-distortion function for the case where the side information is perfectly known to the decoder only. For a given target distortion , in general verifies , where is the rate required to encode if is available to both the encoder and the decoder, and is the minimal rate for encoding without side information (SI). These results give achievable rate bounds, however the design of codes and practical solutions for compression and communication applications remain a widely open issue.
4 Application domains
4.1 Overview
The application domains addressed by the project are:
- Compression with advanced functionalities of various imaging modalities
- Networked multimedia applications taking into account needs in terms of user and network adaptation (e.g., interactive streaming, resilience to channel noise)
- Content editing, post-production, and computational photography.
4.2 Compression of emerging imaging modalities
Compression of visual content remains a widely-sought capability for a large number of applications. This is particularly true for mobile applications, as the need for wireless transmission capacity will significantly increase during the years to come. Hence, efficient compression tools are required to satisfy the trend towards mobile access to larger image resolutions and higher quality. A new impulse to research in video compression is also brought by the emergence of new imaging modalities, e.g. high dynamic range (HDR) images and videos (higher bit depth, extended colorimetric space), light fields and omni-directional imaging.
Different video data formats and technologies are envisaged for interactive and immersive 3D video applications using omni-directional videos, stereoscopic or multi-view videos. The "omni-directional video" set-up refers to 360-degree view from one single viewpoint or spherical video. Stereoscopic video is composed of two-view videos, the right and left images of the scene which, when combined, can recreate the depth aspect of the scene. A multi-view video refers to multiple video sequences captured by multiple video cameras and possibly by depth cameras. Associated with a view synthesis method, a multi-view video allows the generation of virtual views of the scene from any viewpoint. This property can be used in a large diversity of applications, including Three-Dimensional TV (3DTV), and Free Viewpoint Video (FVV). In parallel, the advent of a variety of heterogeneous delivery infrastructures has given momentum to extensive work on optimizing the end-to-end delivery QoS (Quality of Service). This encompasses compression capability but also capability for adapting the compressed streams to varying network conditions. The scalability of the video content compressed representation and its robustness to transmission impairments are thus important features for seamless adaptation to varying network conditions and to terminal capabilities.
4.3 Networked visual applications
Free-viewpoint Television (FTV) is a system for watching videos in which the user can choose its viewpoint freely and change it at anytime. To allow this navigation, many views are proposed and the user can navigate from one to the other. The goal of FTV is to propose an immersive sensation without the disadvantage of Three-dimensional television (3DTV). With FTV, a look-around effect is produced without any visual fatigue since the displayed images remain 2D. However, technical characteristics of FTV are large databases, huge numbers of users, and requests of subsets of the data, while the subset can be randomly chosen by the viewer. This requires the design of coding algorithms allowing such a random access to the pre-encoded and stored data which would preserve the compression performance of predictive coding. This research also finds applications in the context of Internet of Things in which the problem arises of optimally selecting both the number and the position of reference sensors and of compressing the captured data to be shared among a high number of users.
Broadband fixed and mobile access networks with different radio access technologies have enabled not only IPTV and Internet TV but also the emergence of mobile TV and mobile devices with internet capability. A major challenge for next internet TV or internet video remains to be able to deliver the increasing variety of media (including more and more bandwidth demanding media) with a sufficient end-to-end QoS (Quality of Service) and QoE (Quality of Experience).
4.4 Editing, post-production and computational photography
Editing and post-production are critical aspects in the audio-visual production process. Increased ways of “consuming” visual content also highlight the need for content repurposing as well as for higher interaction and editing capabilities. Content repurposing encompasses format conversion (retargeting), content summarization, and content editing. This processing requires powerful methods for extracting condensed video representations as well as powerful inpainting techniques. By providing advanced models, advanced video processing and image analysis tools, more visual effects, with more realism become possible. Our activies around light field imaging also find applications in computational photography which refers to the capability of creating photographic functionalities beyond what is possible with traditional cameras and processing tools.
5 Highlights of the year
5.1 Awards
A. Roumy has received the 2023 IEEE outstanding editorial board award for her activities as associate editor for IEEE Trans. on Image Processing.
The research paper 16 was selected among the Top 3 % of the accepted papers at the 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).
6 New software, platforms, open data
6.1 New software
6.1.1 PnP-A
-
Name:
Plug-and-play algorithms
-
Keywords:
Algorithm, Inverse problem, Deep learning, Optimization
-
Functional Description:
The software is a framework for solving inverse problems using so-called "plug-and-play" algorithms in which the regularisation is performed with an external method such as a denoising neural network. The framework also includes the possibility to apply preconditioning to the algorithms for better performances. The code is developped in python, based on the pytorch deep learning framework, and is designed in a modular way in order to combine each inverse problem (e.g. image completion, interpolation, demosaicing, denoising, ...) with different algorithms (e.g. ADMM, HQS, gradient descent), diifferent preconditioning methods, and different denoising neural networks.
-
Contact:
Christine Guillemot
-
Participants:
Mikael Le Pendu, Christine Guillemot
6.1.2 SIUPPA
-
Name:
Stochastic Implicit Unrolled Proximal Point Algorithm
-
Keywords:
Inverse problem, Optimization, Deep learning
-
Functional Description:
This code implements a stochastic implicit unrolled proximal point method, where an optimization problem is defined for each iteration of the unrolled ADMM scheme, with a learned regularizer. The code is developped in python, based on the pytorch deep learning framework. The unrolled proximal gradient method couples an implicit model and a stochastic learning strategy. For each backpropagation step, the weights are updated from the last iteration as in the Jacobian-Free Backpropagation Implicit Networks, but also from a randomly selected set of unrolled iterations. The code includes several applications, namely denoising, super-resolution, deblurring and demosaicing.
-
Contact:
Christine Guillemot
-
Participants:
Brandon Le Bon, Mikael Le Pendu, Christine Guillemot
6.1.3 DeepULFCam
-
Name:
Deep Unrolling for Light Field Compressed Acquisition using Coded Masks
-
Keywords:
Light fields, Optimization, Deep learning, Compressive sensing
-
Functional Description:
This code implements an algorithm for dense light field reconstruction using a small number of simulated monochromatic projections of the light field. Those simulated projections consist of the composition of: 1) the filtering of a light field by a color coded mask placed between the aperture plane and the sensor plane, performing both angular and spectral multiplexing, 2) a color filtering array performing color multiplexing, 3) a monochromatic sensor. The composition of these processing steps is modeled by a linear projection operator. The light field is then reconstructed by performing the 'unrolling' of an iterative reconstruction algorithm (namely the HQS 'half-quadratic splitting' algorithm, a variant of the ADMM optimization algorithm) using a deep convolutional neural network as proximal operator of the regularizer. The algorithm makes use of the structure of the projection operator to efficiently solve the quadratic data-fidelty minimization sub-problem in closed form. This code is designed to be compatible with Python 3.7 and Tensorflow 2.3. Other required dependencies are: Pillow, PyYAML.
-
Contact:
Guillaume Le Guludec
-
Participants:
Guillaume Le Guludec, Christine Guillemot
6.1.4 OSLO: On-the-Sphere Learning for Omnidirectional images
-
Keywords:
Omnidirectional image, Machine learning, Neural networks
-
Functional Description:
This code implements a deep convolutional neural network for omnidirectional images. The approach operates directly on the sphere, without the need to project the data on a 2D image. More specifically, from the sphere pixelization, called healpix, the code implements a convolution operation on the sphere that keeps the orientation (north/south/east/west). This convolution has the same complexity as a classical 2D planar convolution. Moreover, the code implements stride, iterative aggregation, and pixel shuffling in the spherical domain. Finally, image compression is implemented as an application of this on-the-sphere CNN.
-
Authors:
Navid Mahmoudian Bidgoli, Thomas Maugey, Aline Roumy
-
Contact:
Aline Roumy
6.1.5 JNR-MLF
-
Name:
Joint Neural Representation for Multiple Light Fields
-
Keywords:
Neural networks, Light fields
-
Functional Description:
The code learns a joint implicit neural representation of a collection of light fields. Implicit neural representations are neural networks that represent a signal as a mapping from the space of coordinates to the space of values. For traditional images, it is a mapping from a 2D space to a 3D space. In the case of light field, it is a mapping from a 4D to a 3D space.
The algorithm works by learning a factorisation of the weights and biases of a SIGNET based network. For each layer, a base of matrices is learned that serves as a representation shared between all light fields (a.k.a. scene) of the dataset, together with, for each scene in the dataset, a set of coefficients with respect to this base, which acts as individual representations. The matrices formed by taking the linear combinations of the base matrices with the coefficients corresponding to a given scene serve as the weight matrices of the network. In addition to the set of coefficients, we also learn an individual bias vector for each scene.
The code is therefore composed of two parts: 1)- The representation provider, which takes the index i of a scene, and outputs a weight matrix and bias vector for each layer. 2)- The synthesis network which, using the weights and biases, computes the values of the pixels by querying the network on the coordinates of all pixels. The network is learned using Adam. At each iteration, a light field index i is chosen at random, along with a batch of coordinates, and the corresponding values are predicted, using weights and biases from the representation provider and the synthesis network. The model's parameters U, V and (the relevant column of) Sigma are then updated by gradient backprogagation using a MSE minimization objective. The code uses TensorFlow 2.7.
-
Contact:
Guillaume Le Guludec
-
Participants:
Guillaume Le Guludec, Christine Guillemot
6.1.6 PnP-Reg
-
Keywords:
Inverse problem, Deep learning, Optimization
-
Functional Description:
This is the pytorch implementation of a network directly modeling the gradient of a MAP regularizer. The training of the gradient of the regularizer is done jointly with the training of the corresponding MAP denoiser. This network representing the gradient of an image regularizer can be used in a plug-and-play framework together with gradient-based optimization methods, It can also be used to initialize the regularizer in an unrolled gradient-based optimization framework in which the regularizer can in addition be fine tuned end-to-end for a given task. The code can be used to solve typical inverse problems in imaging such as denoising, deblurring, superresolution or pixel-wise inpainting.
- URL:
-
Contact:
Rita Fermanian
-
Participants:
Rita Fermanian, Christine Guillemot, Mikael Le Pendu
6.1.7 UnrolledFDL
-
Name:
Unrolled Optimization of Fourier Disparity Layers for Light field representation and view synthesis
-
Keywords:
Light fields, Deep learning, Optimization, View synthesis
-
Functional Description:
This code implements a method which reconstruct the light field of a scene from a sparse set of input views taken at a particular viewpoint and at different focal distances, i.e. from a so-called focal stack. By using a focal stack as input, the code allows us to reconstruct the scene light field from images captured by a standard 2D camera. It first performs an unrolled optimization of a Fourier Disparity Layer (FDL) based representation of light fields from the input focal stack. The FDL representation samples the LF in the depth dimension by decomposing the scene as a discrete sum of layers. Once the layers are known, they can be used to produce different viewpoints of the scene while controlling the focus and simulating a camera aperture of arbitrary shape and size.
- URL:
-
Contact:
Brandon Le Bon
-
Participants:
Christine Guillemot, Brandon Le Bon, Mikael Le Pendu
6.1.8 JointFDL-ViewSynthesis
-
Name:
Joint unrolled optimization of FDL light field representation and view synthesis
-
Keywords:
Light fields, Deep learning, Optimization, View synthesis
-
Functional Description:
This code is a pytorch implementation of a method that allows reconstructing the light field of a scene from a focal stack, i.e. a set of images taken at different focus distances using a single traditional camera. The code estimates an FDL light field representation using an unrolled optimization approach and jointly optimizes a convolutional neural network enabling view synthesis. The joint optimization allows an efficient handling of the occlusions issues.
- URL:
-
Contact:
Brandon Le Bon
-
Participants:
Christine Guillemot, Brandon Le Bon, Mikael Le Pendu
7 New results
7.1 Visual Data Analysis
Keywords: 3D modeling, Light-fields, camera design, 3D point clouds, Plenoptic point clouds.
7.1.1 Light field reconstruction from a focal stack with unrolled optimization in the Fourier domain
Participants: Christine Guillemot, Brandon Lebon.
We have addressed the problem of capturing a light field using a single traditional camera, by solving the inverse problem of dense light field reconstruction from a focal stack containing only very few images captured at different focus distances. An end-to-end joint optimization framework has been designed, where a novel unrolled optimization method is jointly optimized with a view synthesis deep neural network. The proposed unrolled optimization method constructs Fourier Disparity Layers (FDL), a compact representation of light fields which samples Lambertian non-occluded scenes in the depth dimension and from which all the light field viewpoints can be computed 24. Solving the optimization problem in the FDL domain allows us to derive a closed-form expression of the data-fit term of the inverse problem. Furthermore, unrolling the FDL optimization allows us to learn a prior directly in the FDL domain 8. In order to widen the FDL representation to more complex scenes, a Deep Convolutional Neural Network (DCNN) is trained to synthesize novel views from the optimized FDL. We show that this joint optimization framework reduces occlusion issues of the FDL model (see Figure 1 below), and outperforms recent state-of-the-art methods for light field reconstruction from focal stack measurements.

7.1.2 Meta-surfaces and image reconstruction co-design for 2D and Light Field microscopy
Participants: Anil Ipek Atalay Appak, Christine Guillemot.
Conventional microscopy systems have limited depth of field, which often necessitates depth scanning techniques hindered by light scattering. Various techniques have been developed to address this challenge, but they have limited extended depth of field (EDOF) capabilities. Extended Depth of Field (EDOF) lenses can solve this problem, however there is a trade-off between the spatial resolution and the depth of field of the captured images.
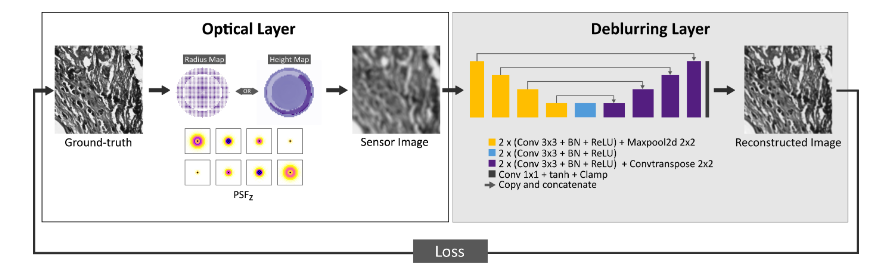
To overcome this challenge, in collaboration with the university of Tampere (Prof. Humeyra Caglayan, Erdem Sahin) in the context of the Plenoptima Marie Curie project, we have adressed this problem of EDOF while preserving a high resolution by designing a pipeline for end-to-end learning and optimization of an optical layer together with a deep learning based image reconstruction method. In our design, instead of phase masks, we consider meta-surface materials. Meta-surfaces are periodic sub-wavelength structures that can change the amplitude, phase, and polarization of the incident wave. The meta-surface parameters are end-to-end optimized to have the highest depth of field with good spatial resolution and high reconstruction quality 7. Our end-to-end optimization framework allows building a computational EDOF microscope that combines a 4f microscopy optical setup incorporating a learned optics at the Fourier plane and a post-processing deblurring neural network (see the illustration of the principle in the Figure 2 below). Utilizing the end-to-end differentiable model, we have introduced a systematic design methodology for computational EDOF microscopy based on the specific visualization requirements of the sample under examination. We have shown that the metasurface optics provides key advantages for extreme EDOF imaging conditions, where the extended DOF range is well beyond what is demonstrated in state of the art, achieving superior EDOF performance.
7.1.3 Vanishing points aided Hash-Frequency Encoding for Neural Radiance Fields (NeRF) estimation from Sparse 360°Input
Participants: Kai Gu, Christine Guillemot, Thomas Maugey.
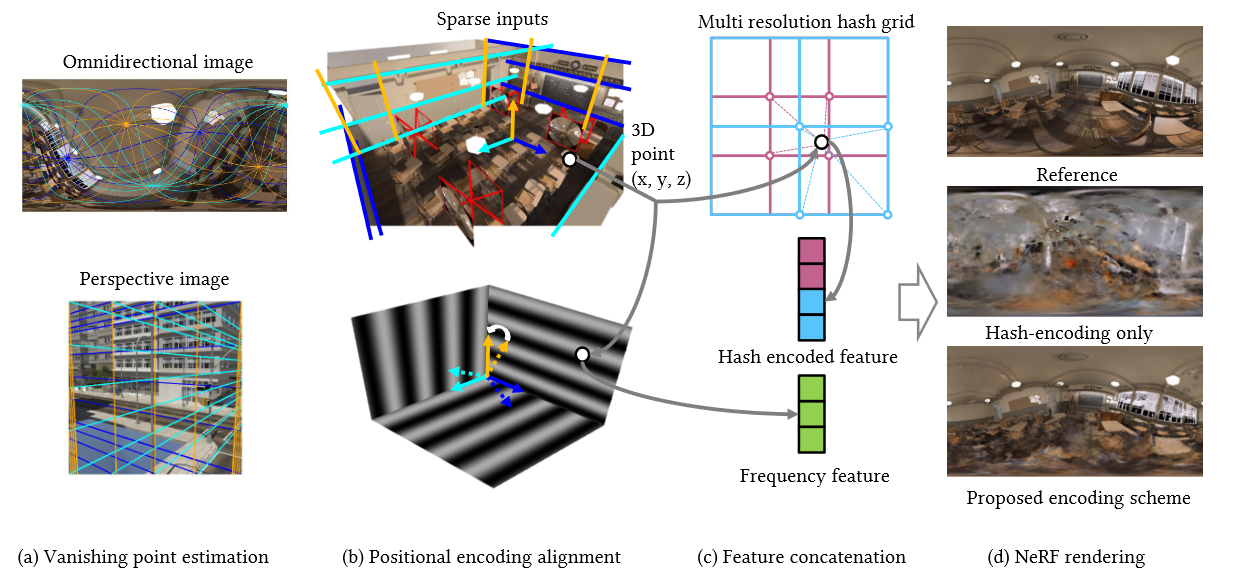
Neural Radiance Fields (NeRF) enable novel view synthesis of 3D scenes when trained with a set of 2D images. One of the key components of NeRF is the input encoding, i.e. mapping the coordinates to higher dimensions to learn high-frequency details, which has been proven to increase the quality. Among various input mappings, hash encoding is gaining increasing attention for its efficiency. However, its performance, when using sparse inputs, is limited. To address this limitation, we have proposed a new input encoding scheme that improves hash-based NeRF for sparse inputs, i.e. few and distant cameras, specifically for 360◦ view synthesis 21. We have combined frequency encoding and hash encoding and shown that this combination can increase dramatically the quality of hash-based NeRF for sparse inputs. Additionally, we have explored scene geometry by estimating vanishing points in omnidirectional images (ODI) of indoor and city scenes in order to align frequency encoding with scene structures (see Figure 3 below). We have shown that our vanishing point-aided scene alignment further improves deterministic and non-deterministic encodings on image regression (view reconstruction and rendering) and view synthesis tasks, where sharper textures and more accurate geometry of scene structures can be reconstructed.
7.2 Signal processing and learning methods for visual data representation and compression
Keywords: Sparse representation, data dimensionality reduction, compression, scalability, rate-distortion theory.
7.2.1 Joint compression, demosaicing and denoising of satellite images
Participants: Denis Bacchus, Christine Guillemot, Aline Roumy.
Today’s satellite images have a high resolution, thanks to high-performance sensors. This increase in the volume of data to be transmitted to Earth requires efficient compression methods. Designing efficient compression algorithms for satellite images must take into account several constraints. First, (i) it must be well adapted to the raw data format. In particular, we have considered the cameras for the Lion satellite constellation with ultra-high spatial resolution at the price of a lower spectral resolution. More precisely, the three spectral bands (RGB) are acquired with a single sensor with an in-built colour filter array. Second, (ii) it should be adapted to the image statistics. Indeed, satellite mages contain very high-frequency details with small objects spread over very few pixels only. Finally, (iii) the compression must be quasi-lossless to allow accurate on-ground interpretation. In addition, the images are also affected by noise during the acquisition process, which hinders the compression process.
While existing compression solutions mostly assume that the captured raw data has been demosaicked prior to compression, we have designed an end-to-end trainable neural network for joint decoding, demosaicking and denoising satellite images on the ground at the decoder side, while encoding the raw data. We have first introduced a training loss combining a perceptual loss with the classical mean square error, which has been shown to better preserve the high-frequency details present in satellite images. We then developed a multi-loss balancing strategy which significantly improves the performance of the proposed joint demosaicking-compression solution 16. We also proposed a novel guidance branch which is used during training, to enforce intermediate features of the demosaicked and decoded images to be close to those that would be obtained with ground truth full colour (non-mosaicked) images during decoding. We have shown that our method achieves better rate-distortion trade-offs compared with current satellite baselines while reducing the overall complexity 42.
We also addressed the limitations of learned image compression neural networks, which have difficulties adapting to certain satellite image characteristics, especially high frequencies that disappear at a high bit-rate in the blur generated in the reconstruction. To answer this problem we described in 15 a joint end-to-end trainable neural network. It is separated into a general compression network and a smaller specialized network. We trained this specialized network to compress the residual part of the image to best preserve the high-frequency details present in the satellite images. The proposed model achieves higher rate-distortion performance than current lossy image compression standards and also manages to retrieve details previously poorly reconstructed.
7.2.2 Plenopic Point Clouds modeling and compression
Participants: Davi Freitas, Christine Guillemot.
Modeling 3D scenes from image data to render novel photorealistic views has been a central topic in the field of computer graphics and vision. The most recent advances have come from the use of neural volumetric representations, such as the volumetric Neural Radiance Fields (NeRF). Although the implicit representation of NERF is able to encapsulate the scene information, its rendering is slow. PlenOctree (Plenoptic Octrees) models have been proposed in order to cope with the rendering speed issue.
A scene is first encoded in a NeRF-like network through training. However, instead of predicting the RGB color of each pixel in each view directly, the network predicts spherical harmonic coefficients. The spherical harmonics are sherical basis functions which allow the encoding of the appearances and preserve view-dependent effects such as specularities. The color is then calculated by summing the weighted spherical harmonic bases evaluated at the corresponding ray direction. The spherical harmonics enable the representation to model view-dependent appearance. To build the PlenOctree model, the NERF-SH model is densely sampled. This allows extracting the octree parameters (the density σ, and the Spherical Harmonics (SH) coefficients for each octant) and thus generate the octree-based radiance field. Then, this octree model is fine-tuned and compressed, e.g. by controlling the visibility thtreshold and the number of spherical harmonics. However, decreasing the number of harmonics affects the capability to represent view-dependent effects, such as specularity and non- Lambertian surfaces, and this proves to be the biggest bottleneck to reduce the bit rate. Plenoctree models have a large size, which is an issue for storage and transmission.
We have addressed this weakness by proposing an efficient compression scheme for the plenoctree model which allows maintaining high rendering quality and speed. The proposed approach both improves the training of the plenoctree model with geometry and sparsity contrained regularization, reduces the number of occupied voxels by controlling the visibility threshold, and then efficiently encodes the spherical harmonics. Results over a set of test camera poses show that we can reduce about eight times the bit rates of the encoded models and still obtain a higher quality of the synthesized images when compared to the original PlenOctree models or, alternatively, a reduction of about 50 times while presenting minimal degradation for novel view synthesis 20.
7.2.3 Joint Neural and Implicit Representations for Multiple Light Fields
Participants: Christine Guillemot, Remy Leroy.
Neural implicit representations have appeared as promising techniques for representing a variety of signals, among which light fields, offering several advantages over traditional grid-based representations, such as independence to the signal resolution. While it has been shown to be a good representation for a given type of signal, i.e. for a particular light field, we realized that exploiting the features shared between different scenes remains an understudied problem. We have therefore made one step towards this end by developing a method for sharing the representation between thousands of light fields, splitting the representation between a part that is shared between all light fields and a part which varies individually from one light field to another 25.
Assuming that the neural representations of the different scenes lie on a manifold, the algorithm learns a factorisation (in the same vein as a singular value decomposition) of the weights matrices forming the layers of a deep neural network, to learn the basis defining the common manifold. For each layer, a base of matrices and is thus learned that serves as a representation shared between all light fields (a.k.a. scene) of the dataset, together with, for each scene in the dataset, a set of coefficients with respect to this base, which acts as individual representations. The matrices formed by taking the linear combinations of the base matrices with the coefficients corresponding to a given scene serve as the weight matrices of the network. In addition to the set of coefficients, we also learn an individual bias vector for each scene. The architecture is therefore composed of two parts: 1)- a representation provider, which takes the index i of a scene, and outputs a weight matrix and bias vector for each layer. 2)- The synthesis network which, using the weights and biases, computes the values of the pixels by querying the network on the coordinates of all pixels. The model's parameters U, V and (the relevant column of) are then updated by gradient backprogagation using a MSE minimization objective.
We have shown that this joint representation possesses good interpolation properties, and allows for a more light-weight storage of a whole database of light fields, exhibiting a ten-fold reduction in the size of the representation when compared to using a separate representation for each light field. Based on these results, we have then focused on the problem of generalizability of this learned joint representation to new scenes that have not been seen during training.
7.2.4 Graph Neural Networks on Large Graphs
Participants: Nicolas Keriven.
Graph Neural Networks (GNN) have become the de-facto deep architectures for most learning problems on data structured as graphs, such as graphs and nodes classification or regression, learning-based graph sampling or graph compression, and so on. Nevertheless, GNN act on different irregular domains represented by one or several graphs that may vary between the training phase and the testing phase, which severely constrain the manner in which they can be built compared to traditional Convolutional Neural Network, as they must respect rules of permutation invariance and equivariance. Moreover, in the absence of traditional convolution, computational complexity quickly becomes an issue, as modern graphs can comprise several millions of nodes. As a result, GNNs encounter many unique challenges limiting their performance, and a better understanding of their theoretical and empirical properties is required to adress them.
We have produced a new analysis of the properties of GNNs on large graphs by leveraging random graphs models, which are traditionally used to represent graphs sampled from manifolds, or real-world large graphs such as relational databases. In 22, we completely characterize the function space that such GNN can produce in the infinite-node limit, which emphasize GNNs' strength but also limitations. We outline the role of so-called graph Positional Encodings, a recent methodology inspired by Transformer models. In 35, we examine the effects of a crucial part in every GNN architecture on this infinite-node limit, the so-called aggregation function. We outline how different functions used in practice yield extremely different rates of convergence to the limit. Finally, in 36, we characterize the generalization properties of simple estimators related to the message-passing process at the core of GNNs on random graphs, a first step toward a more complete characterization.
7.3 Algorithms for inverse problems in visual data processing
Keywords: Inpainting, denoising, view synthesis, super-resolution.
7.3.1 Plug-and-play optimization and learned priors
Participants: Rita Fermanian, Christine Guillemot.
Recent optimization methods for inverse problems have been introduced with the goal of combining the advantages of well understood iterative optimization techniques with those of learnable complex image priors. A first category of methods, referred to as ”Plug-and-play” methods, has been introduced where a learned network-based prior is plugged in an iterative optimization algorithm. These learnable priors can take several forms, the most common ones being: a projection operator on a learned image subspace, a proximal operator of a regularizer or a denoiser. Plug-and-Play optimization methods have in particular been introduced for solving inverse problems in imaging by plugging a denoiser into the ADMM (Alternating Direction Multiplier Method) optimization algorithm. The denoiser accounts for the regularization and therefore implicitly determines the prior knowledge on the data, hence replacing typical handcrafted priors.
In the context of the AI chair DeepCIM, we have shown that it is possible to train a network directly modeling the gradient of a MAP regularizer while jointly training the corresponding MAP denoiser. We have used this network in gradient-based optimization methods and obtain better results comparing to other generic Plug-and-Play approaches. We have also shown that the regularizer can be used as a pre-trained network for unrolled gradient descent. Lastly, we have shown that the resulting denoiser allows for a better convergence of the Plug-and-Play ADMM.
Although the design of learned denoisers has garnered significant research attention in the context of traditional 2D images, omnidirectional image denoising has received relatively limited attention in the literature. Furthermore, extending processing models and tools designed for 2D images to the sphere presents many challenges due to the inherent distortions and non-uniform pixel distributions associated with spherical representations and their underlying projections. We have addressed the problem of omnidirectional image denoising and studied the advantage of denoising the spherical image directly rather than its mapping 49. We have introduced a novel network called SphereDRUNet to denoise spherical images using deep learning tools on a spherical sampling. We have shown that denoising directly the sphere using our network gives better performance, compared to denoising the projected equirectangular images with a similarly learned model.
7.3.2 Unrolled deep equilibrium models for multi-tasks inverse problems
Participants: Christine Guillemot, Samuel Willingham.
One advantage of plug-and-play methods with their learned priors is their genericity in the sense that they can be used for any inverse problem, and do not need to be re-trained for each new problem, in contrast with deep models learned as a regression function for a specific task. However, priors learned independently of the targeted problem may not yield the best solution. Unrolling a fixed number of iterations of optimization algorithms is another way of coupling optimization and deep learning techniques. The learnable network is trained end to- end within the iterative algorithm so that performing a fixed number of iterations yields optimized results for a given inverse problem. Several optimization algorithms (Iterative Shrinkage Thresholding Algorithm (ISTA), Half S Quadratic Splitting (HQS), and Alternating Direction Method of Multipliers (ADMM)) have been unrolled in the literature, where a learned regularization network is used at each iteration of the optimization algorithm. While usual iterative methods iterate until idempotence, i.e. until the difference between the input and the output is sufficiently small, the number of iterations in unrolled optimization methods is set to a small value, to cope with memory issues.
Another approach to cope with the memory issue of unrolled optimization methods is the Deep equilibrium (DEQ) model which extends unrolled methods to have a theoretically infinite amount of iterations by leveraging fixed-point properties. This allows for simpler back-propagation, which can even be done in a Jacobian-free manner. The resulting back-propagation has a memory-footprint independent of the number of iterations used. Deep equilibrium models, indeed avoid large memory consumption by back-propagating through the architecture’s fixed point. This results in an architecture that is intended to converge and allows for the prior to be more general. However, unrolled methods train a network end-to-end for a specific degradation and necessitate retraining for each specific degradation.
We have leveraged deep equilibrium models to train a plug-and-play style prior that can be used to solve inverse problems for a range of tasks 32. Deep equilibrium models (DEQs), iterate an unrolled method until convergence and thereby enable end-to-end training on the reconstruction error with simplified back-propagation. We have investigated to what extent a solution for several inverse problems can be found by employing a multi-task DEQ. This MT-DEQ is used to train a prior on the actual estimation error, in contrast to a theoretical noise model used for plug-and-play methods. This has the advantage that the resulting prior is trained for a range of degradations beyond pure Gaussian denoising.
7.3.3 Low light image restoration
Participants: Christine Guillemot, Arthur Lecert, Aline Roumy.
The Retinex theory is particularly well suited to the restoration of nighttime images, as it can be used to decompose an image into the illumination of the scene and its reflectance. It is however not well suited for outdoor scenes where we can have colored light. In addition, it does not take into account the non linearities present in the image acquisition pipeline. We have therefore revisited the retinex model to better take into account the physics of light, i.e. by including a colored illumination, and by taking into account some non linearities of the acquisition pipeline.
Based on this new decomposition model, we have proposed a deep learning-based architecture inspired by the style transfer methods, with two generative adversarial networks (GAN) trained in an unsupervised manner 11. This deep neural network is composed of two branches, one for each of the components (illumination and reflectance) and includes instance normalization, as done in style transfer, to enforce a better separation between the style (illumination) and the content (reflectance), and thus better handle the component separation problem. The network is trained with additional loss terms corresponding to physical priors, the reflectance being the shared information between the night and daylight image distributions.
7.4 User centric compression
Keywords: Information theory, interactive communication, coding for machines, generative compression, database sampling.
7.4.1 Compression with a helper: zero-error compression bounds
Participants: Nicolas Charpenay, Aline Roumy.
Zero-error source coding is at the core of practical compression algorithms. Here, zero error refers to the case where the data is decompressed without any error for any block-length. This must be differentiated from the vanishing error setup, where the probability of error of the decompressed data decreases to zero as the length of the processed data tends to infinity. In point-to point communication (one sender/one receiver), zero-error and vanishing-error information theoretic compression bounds coincides. This is however not the case in networks, with possibly many senders and/or receivers. For instance, in the source coding problem with a helper at the decoder, the compression bounds under both hypotheses do no coincide. More precisely, there exist examples, where both bounds differ. But more importantly, the zero-error compression characterization for the general case is still an open problem. This is due to the fact that the compression bounds are given by the so-called complementary graph entropy, which requires to compute the coloring of an infinite product of graphs. Therefore, this complementary graph entropy has no single-letter formula, except for some particular cases such as: perfect graphs, the pentagon graph, and their disjoint union. In 18, we derived a structural result that equates the complementary graph entropies of AND product and disjoint unions (up to a multiplicative constant), which has two consequences. First, we prove that the cases where the complementary graph entropies of these two compositions (AND product and disjoint union) can be linearized coincide. Second, we determine the complementary graph entropies in cases where it was unknown: AND products of perfect graphs; product of perfect graph and the pentagon graph, which are not perfect in general.
7.4.2 Coding for Machine: zero-error compression bounds
Participants: Nicolas Charpenay, Aline Roumy.
Due to the ever-growing amount of visual data produced and stored, there are now evidences that these data will not only be viewed by humans but also processed by machines. In this context, practical implementations aim to provide better compression efficiency when the primary consumers are machines that perform certain computer vision tasks. One difficulty arises from the fact that these tasks are not known upon compression. This problem has been studied in Information theory and is called the coding for computing problem. However, no single letter formula exists for this problem, due to the fact that the optimal coding performance depends on an infinite product of characteristic graphs, that represents the joint distribution of the data and the tasks. In 19, we introduced a generalization of this problem, where the encoder has some partial information about the request, for instance the type of the request that will be made at the decoder. We proposed a condition, which allows to have a single letter characterization of the optimal compression performance.
7.4.3 Coding for Machine: learning on Entropy Coded Images with CNN
Participants: Rémi Piau, Thomas Maugey, Aline Roumy.
Learning on entropy coded data has many benefits. First, it avoids decoding, but also it allows one to process compact data. However, this type of learning has been overlooked due to the chaos introduced by entropy coding functions.
In 29, we proposed an empirical study to see whether learning with convolutional neural networks (CNNs) on entropy coded data is possible. First, we define spatial and semantic closeness, two key properties that we experimentally show to be necessary to guarantee the efficiency of the convolution. Then, we show that these properties are not satisfied by the data processed by an entropy coder. Despite this, our experimental results show that learning in such difficult conditions is still possible, and that the performances are far from a random guess. These results have been obtained thanks to the construction of CNN architectures designed for 1D data (one based on VGG, the other on ResNet). Finally, we propose some experiments that explain why CNN are still performing reasonably well on entropy coded data.
In 30, we introduced a new metric that measures the chaos in the data representation. This measure is easy to compute as it depends on the encoded data only. Moreover, for a family of entropy coders, this measure allows one to predict the accuracy of the learning algorithm that process entropy coded data.
7.4.4 Generative compression of images at extremely low bitrates
Participants: Tom Bordin, Thomas Maugey.
An image is traditionally compressed with the aim of minimizing the error made in the reconstruction. The Mean Squared Error (MSE) naturally comes as a simple and efficient criterion to evaluate the fidelity of the output in terms of distortion. This metric remains widely used to evaluate methods compressing images ranging from high to low bitrates. But what happens when compression is pushed to the extreme ( bpp)? While excessive compression of sensitive data such as movies or vacations photos is not desirable, a drastic reduction of storage could be welcomed for the so-called "cold data". This massive amount of data that is stored but almost never accessed is estimated to represent of today's storage while projected to become by 2025. In that case, compression at extremely low bitrates could be an alternative to deleting potentially useful data or keeping a huge amount of data that might not be used. However, when targeting such bitrates, the relevance of the MSE as an evaluation criterion drops. Indeed, there exists a tradeoff between the perceived quality of the output and the fidelity in terms of pixels. This is called the perception-distortion tradeoff. Moreover, it is shown that decreasing the bitrate exacerbates the opposing goals of the two metrics. Optimization of the MSE then leads to the apparition of numerous compression artifacts, which makes the use of such bitrates really unattractive.
In that context, we proposed in 17 a framework for image compression in which the fidelity criterion is replaced by a semantic and quality preservation objective. Encoding the image thus becomes a simple extraction of semantic, enabling to reach drastic compression ratios. The decoding side is handled by a generative model relying on the diffusion process for the reconstruction of images. We first propose to describe the semantic using low resolution segmentation maps as guide. We further improve the generation, introducing color maps guidance without retraining the generative decoder. We show that it is possible to produce images of high visual quality with preserved semantic at extremely low bitrates when compared with classical codecs (see Figure below).

7.4.5 Image Embedding and User Multi-preference Modeling for Data Collection Sampling
Participants: Thomas Maugey.
Image sampling based on user perception has recently increased interest given the unstoppable increase of stored datasets. For example, let's think of the large-scale image collections associated with Instagram and other social media accounts, online retailers, or your own personal photo Gallery saved on the cloud. Storing such large-scale datasets has become a big burden, from an economical as well as sustainability perspective. Traditional image data sampling methods can be understood as a way to alleviate such burden, by retaining only pictures from a dataset with the ideal goal of providing a summary (in the sense of a brief description) of the database. The challenging aspect is however to understand which is the best set of images to select (not to delete), especially given the user's preferences. This is highly challenging as the user will perceive the deleted images as lost information.
In 14, we proposed an end-to-end user-centric sampling method aimed at selecting the images from an image collection that are able to maximize the information perceived by a given user. As main contributions, we first introduce novel metrics that assess the amount of perceived information retained by the user when experiencing a set of images. Given the actual information present in a set of images, which is the volume spanned by the set in the corresponding latent space, we show how to take into account the user's preferences in such a volume calculation to build a user-centric metric for the perceived information. Finally, we propose a sampling strategy seeking the minimum set of images that maximize the information perceived by a given user. Experiments using the coco dataset show the ability of the proposed approach to accurately integrate user preference while keeping a reasonable diversity in the sampled image set.
7.4.6 A Water-filling Algorithm Maximizing the Volume of Submatrices Above the Rank
Participants: Claude Petit, Aline Roumy, Thomas Maugey.
In 28, we proposed an algorithm to extract, from a given rectangular matrix, a submatrix with maximum volume, whose number of extracted columns is greater than the initial matrix rank. This problem arises in compression and summarization of databases, recommender systems, learning, numerical analysis or applied linear algebra. We use a continuous relaxation of the maximum volume matrix extraction problem, which admits a simple and closed form solution: the nonzero singular values of the extracted matrix must be equal. The proposed algorithm extracts matrices with singular values, which are close to be equal. It is inspired by a water-filling technique, traditionally dedicated to equalization strategies in communication channels. Simulations show that the proposed algorithm performs better than sampling methods based on determinantal point processes (DPPs) and achieves similar performance as the best known algorithm, but with a lower complexity.
7.4.7 Towards digital sobriety: why improving the energy efficiency of video streaming is not enough
Participants: Thomas Maugey.
In 2018, online video streaming constituted of the global data flow, and, by itself, generated of the global emissions (as much as a country like Spain emits). And this quantity explodes: video traffic is estimated to grow by 79 between 2021 and 2027. At the same time, the sixth report of the Intergovernmental Panel on Climate Change (IPCC) states that if we want to keep the global warming under 1.5°C (Paris agreement), one should target a global emissions decrease of when compared to those of 2019. This corresponds to a decrease of per year. They also state that this is not the path that is currently taken. Hence, every part of our society must urgently aim sobriety. This is for example the case of online video streaming. So the question is simple: what are the solutions that should be envisaged to halve by 2030 the GHG emissions due to video streaming ?
As these emissions are correlated (not necessarily proportional) to the video data flow, one could rely on the progress of video compression algorithms to decrease the size of every individual video. For example, the last H.266/VVC standard reaches of gain when compared with the previous codec H.265/HEVC published 7 years before. Even though similar gains can be expected for the future codec, this cannot, by itself, enables a drastic emissions reduction, because of at least three reasons. First, the size reduction is achieved on individual videos and not on the global flow. In other words, video compression does not fight against the number of videos that is created or consumed. Yet, this amount of video streamed will explode in the coming years. Second, compression gains are usually not exploited to decrease the required bandwidth but rather to increase the video resolution or to create new video usages (IoT, Virtual Reality, etc.). Last, compression gains are achieved only at the expense of huge algorithm complexity. Encoding a video becomes more and more complex and thus requires, for each codec, more energy Another cause of video streaming gas emissions is precisely the complexity of the operations all along the transmission chain (including the video coding algorithms as mentioned just above). Intensive research efforts have been made to decrease this complexity and thus the consumed energy.
Even though these research results are crucial and make the energy expenditure more optimized, we demonstrate in 27 that this is insufficient to achieve the goal set by the IPCC. We build a simple model derived from the Kaya identity. This model enables to compare the order of magnitude of the energy reduction on one side and the digital affluence on the other side. Results show that even drastic energy reduction cannot cope with the forecasted video data flow explosion. Said differently, to achieve Paris agreement objectives (half emissions in 2030 when compared to 2019), the academic, industrial and politic actors must also consider laws and regulation to limit the video data consumption.
8 Bilateral contracts and grants with industry
8.1 Bilateral contracts with industry
CIFRE contract with Ateme on neural networks for video compression
Participants: Christine Guillemot, Yiqun Liu, Aline Roumy.
- Title : Neural networks for video compression of reduced complexity
- Partners : Ateme (T. Guionnet, M. Abdoli), Inria-Rennes.
- Funding : Ateme, ANRT.
- Period : Aug.2020-Jul.2023.
The goal of this Cifre contract is to investigate deep learning architectures for the inference of coding modes in video compression algorithms with the ultimate goal of reducing the encoder complexity. The first step addresses the problem of Intra coding modes and quad-tree partitioning inference. The next step will consider Inter coding modes taking into account motion and temporal information.
CIFRE contract with TyndallFX on Radiance fields representation for dynamic scene reconstruction
Participants: Stephane Belemkoabga, Christine Guillemot, Thomas Maugey.
- Title : Radiance fields representation for dynamic scene reconstruction
- Partners : TyndallFX (M. Hudon, R. Mallart), Inria-Rennes.
- Funding : TyndallFX, ANRT.
- Period : Oct.2023-Sept.2026.
The goalf of this project is to design novel methods for modeling and compact representation of radiance fields for scene reconstruction and view synthesis. The problems that are addressed are those of fast and efficient estimation of the camera pose parameters and of the 3D model of the sceen based on Gaussian splatting, and as as the one of tracking and modeling the deformation of the model due to the global camera motion and to the motion of the different objects in the scene.
Contract LITCHIE with Airbus on deep learning for satellite imaging
Participants: Denis Bacchus, Christine Guillemot, Arthur Lecert, Aline Roumy.
- Title : Deep learning methods for low light vision
- Partners : Airbus (R. Fraisse), Inria-Rennes.
- Funding : BPI.
- Period : Sept.2020-Aug.2023.
The goal of this contract is to investigate deep learning methods for low light vision with sattelite imaging. The SIROCCO team focuses on two complementary problems: compression of low light images and restoration under conditions of low illumination, and hazing. The problem of low light image enhancement implies handling various factors simultaneously including brightness, contrast, artifacts and noise. We investigate solutions coupling the retinex theory, assuming that observed images can be decomposed into reflectance and illumination, with machine learning methods. We address the compression problem taking into account the processing tasks considered on the ground such as the restoration task, leading to an end-to-end optimization approach.
Cifre contract with MediaKind on Multiple profile encoding optimization
Participants: Reda Kaafarani, Thomas Maugey, Aline Roumy.
- Title : Multiple profile encoding optimization
- Partners : MediaKind, Inria-Rennes.
- Funding : MediaKind, ANRT.
- Period : April 2021-April 2024.
The goal of this Cifre contract is to optimize a streaming solution taking into the whole process, namely the encoding, the long-term and the short term storages (in particular for replay, taking into the popularity of the videos), the multiple copies of a video (to adapt to both the resolution and the bandwidth of the user), and the transmissions (between all entities: encoder, back-end and front-end server, and the user). This optimization will be with several objectives as well. In particular, the goals will be to maximize the user experience but also to save energy and/or the deployment cost of a streaming solution.
9 Partnerships and cooperations
9.1 European initiatives
9.1.1 H2020 projects
PLENOPTIMA: Marie Sklodowska-Curie Innovative Training Network
Participants: Anil Atalay Appak, Davi Freitas, Christine Guillemot, Kai Gu, Thomas Maugey, Soheib Takhtardeshir, Samuel Willingham.
PLENOPTIMA project on cordis.europa.eu
-
Title:
Plenoptic Imaging
-
Duration:
From January 1, 2021 to December 31, 2024
-
Partners:
- Institut National de Recherche en Informatique et Automatique (INRIA), France
- Mittunivercitetet (MIUN), Sweden
- Technische Universitat Berlin (TUB), Germany
- Tampereen Korkeakoulusaatio (TAMPERE UNIVERSITY), Finland
- Institute of Optical Material and Technologies, Bulgarian Academy of Sciences (IOMT), Bulgaria
-
Inria contact:
Christine Guillemot
- Coordinator:
-
Summary:
Plenoptic Imaging aims at studying the phenomena of light field formation, propagation, sensing and perception along with the computational methods for extracting, processing and rendering the visual information.
The PLENOPTIMA ultimate project goal is to establish new cross-sectorial, international, multi-university sustainable doctoral degree programmes in the area of plenoptic imaging and to train the first fifteen future researchers and creative professionals within these programmes for the benefit of a variety of application sectors. PLENOPTIMA develops a cross-disciplinary approach to imaging, which includes the physics of light, new optical materials and sensing principles, signal processing methods, new computing architectures, and vision science modelling. With this aim, PLENOPTIMA joints five of the strongest research groups in nanophotonics, imaging and machine learning in Europe with twelve innovative companies, research institutes and a pre-competitive business ecosystem developing and marketing plenoptic imaging devices and services.
PLENOPTIMA advances the plenoptic imaging theory to set the foundations for developing future imaging systems that handle visual information in fundamentally new ways, augmenting the human perceptual, creative, and cognitive capabilities. More specifically, it develops 1) Full computational plenoptic imaging acquisition systems; 2) Pioneering models and methods for plenoptic data processing, with a focus on dimensionality reduction, compression, and inverse problems; 3) Efficient rendering and interactive visualization on immersive displays reproducing all physiological visual depth cues and enabling realistic interaction.
All ESRs are registered in Joint/Double degree doctoral programmes at academic institutions in Bulgaria, Finland, France, Germany and Sweden.
9.2 National initiatives
9.2.1 IA Chair: DeepCIM- Deep learning for computational imaging with emerging image modalities
Participants: Rita Fermanian, Christine Guillemot, Brandon Lebon, Remy Leroy.
-
Funding
: ANR (Agence Nationale de la Recherche).
-
Period
: Sept. 2020 - Aug. 2024.
-
Inria contact
: Christine Guillemot
-
Summary:
The project aims at leveraging recent advances in three fields: image processing, computer vision and machine (deep) learning. It will focus on the design of models and algorithms for data dimensionality reduction and inverse problems with emerging image modalities. The first research challenge will concern the design of learning methods for data representation and dimensionality reduction. These methods encompass the learning of sparse and low rank models, of signal priors or representations in latent spaces of reduced dimensions. This also includes the learning of efficient and, if possible, lightweight architectures for data recovery from the representations of reduced dimension. Modeling joint distributions of pixels constituting a natural image is also a fundamental requirement for a variety of processing tasks. This is one of the major challenges in generative image modeling, field conquered in recent years by deep learning. Based on the above models, our goal is also to develop algorithms for solving a number of inverse problems with novel imaging modalities. Solving inverse problems to retrieve a good representation of the scene from the captured data requires prior knowledge on the structure of the image space. Deep learning techniques designed to learn signal priors, can be used as regularization models.
9.2.2 CominLabs Colearn project: Coding for Learning
Participants: Thomas Maugey, Rémi Piau, Aline Roumy.
- Partners: Inria-Rennes (Sirocco team); LabSTICC, IMT Atlantique, (team Code and SI); IETR, INSA Rennes (Syscom team).
- Funding: Labex CominLabs.
- Period: Sept. 2021 - Dec. 2024.
The amount of data available online is growing so fast that it is essential to rely on advanced Machine Learning techniques so as to automatically analyze, sort, and organize the content uploaded by e.g. sensors or users. The conventional data transmission framework assumes that the data should be completely reconstructed, even with some distortions, by the server. Instead, this project aims to develop a novel communication framework in which the server may also apply a learning task over the coded data. The project will therefore develop an Information Theoretic analysis so as to understand the fundamental limits of such systems, and develop novel coding techniques allowing for both learning and data reconstruction from the coded data.
9.2.3 ANR Young researcher grant: MAssive multimedia DAta collection REpurposing (MADARE)
Participants: Tom Bordin, Thomas Maugey.
- Funding: ANR (Agence Nationale de la Recherche).
- Period: Apr. 2022 - Oct. 2025.
Compression algorithms are nowadays overwhelmed by the tsunami of visual data created everyday. Despite a growing efficiency, they are always constrained to minimize the compression error, computed in the pixel domain. The Data Repurposing framework, proposed in the MADARE project, will tear down this barrier, by allowing the compression algorithm to “reinvent” part of the data at the decoding phase, and thus saving a lot of bit-rate by not coding it. Concretely, a data collection is only encoded to a compact description that is used to guarantee that the regenerated content is semantically coherent with the initial one.
In practice, it opens several research directions: how to organise the latent space (in which the coded descriptions lie) such that the information is efficiently and intelligibly represented ? How to regenerate a synthesized content from this compact description (based for example on guided diffusion algorithms) ? Finally, how to extend this idea to video ?
By revisiting the compression problem, the MADARE project aims gigantic compression ratios enabling, among other benefits, to reduce the impact of exploding data creation on the cloud servers’ energy consumption.
10 Dissemination
Participants: Christine Guillemot, Nicolas Keriven, Thomas Maugey, Aline Roumy.
———————————–
10.1 Promoting scientific activities
10.1.1 Scientific events: organisation
General chair, scientific chair
- C. Guillemot has organized the Plenoptima training school on plenoptic processing and compression as well as the Plenoptima workshop on innovation and project management (26-30 June 2023).
10.1.2 Scientific events: selection
Member of the conference program committees
- A. Roumy was a member of the technical program committee of the (Conference on Computer Vision and Pattern Recognition) CVPR 2023 workshop on New Trends in Image Restoration and Enhancement (NTIRE).
- A. Roumy was a member of the technical program committee of the 2023 National Signal Processing workshop (colloque GRETSI).
10.1.3 Journal
Member of the editorial boards
- C. Guillemot has been associate editor of the International Journal on Mathematical Imaging and Vision (2016-2023).
- T. Maugey is associate editor of the EURASIP Journal on Advances in Signal Processing.
- T. Maugey is associate editor of the IEEE Signal Processing Letter.
- A. Roumy was Associate Editor of the IEEE Transactions on Image Processing until Nov. 2023.
- A. Roumy is Senior Associate Editor of the IEEE Transactions on Image Processing since Nov. 2023.
10.1.4 Leadership within the scientific community
- A. Roumy is member of the IEEE IVMSP technical committee.
- A. Roumy is a member of the Executive board of the National Research group in Image and Signal Processing (GRETSI).
- T. Maugey is member of the EURASIP Technical Area Committee (Visual Information Processing) since Jan 2023 for a four-year term.
10.1.5 Research administration
- C. Guillemot was a member of the "Bureau du Comité des Projets" (until Dec. 2023)
- C. Guillemot is a member of the research commission of the University of Rennes, as Inria representative
- A. Roumy has been a member of Inria evaluation committee (until June 2023)
- A. Roumy is a member of the research commission and of the academic board of the University of Rennes 2, as Inria representative
- A. Roumy has been a member of the jury for the recruitment of Inria Junior researcher (CRCN/ISFP) in Lyon, and of the jury of the recruitment of Inria senior researchers
- A. Roumy has been a member of the Inria Delegation committee of the Inria center at Rennes University
- T. Maugey has been a member of the jury for the recruitment of Inria Junior researcher (CRCN/ISFP) in Rennes
10.2 Teaching - Supervision - Juries
10.2.1 Teaching
- T. Maugey has given a course on Graph Image Processing, 10 hours, M2 SiVOS, Univ. of Rennes 1, France.
- T. Maugey has given a course on Representation, editing and perception of digital images, 21 hours, M2 SIF, Univ. of Rennes 1, France.
- A. Roumy has given a Engineering degree course on Image and Video compression, 10 hours, University Rennes 1, ESIR, France.
- N. Keriven has given a course on Machine Learning, 24 hours, ENSTA Paris, France.
- N. Keriven has given a course on Signal Processing, 12 hours, ENS Rennes, France.
- N. Keriven has given a course on Sparsity and COmpressed Sensing, 12 hours, INSA Rennes, France.
10.2.2 Supervision
- C. Guillemot and A. Roumy have been co-supervising the PhD thesis of D. Bacchus and A. Lecert in the context of the Litchie project with Airbus, and the PhD thesis of Y. liu in the context of the Cifre contract with Ateme.
- C. Guillemot has been supervising the PhD thesis of B. Lebon and R. Fermanian in the context of the AI chair DeepCIM funded by the ANR.
- C. Guillemot and T. Maugey are co-supervising the PhD thesis of S. Belemkoabga in the context of the Cifre contract with TyndallFX.
- C. Guillemot is co-supervising the double degree PhD thesis of S. Willingham (together with M. Sojstrom from MidSeden University), of S. Takhtardeshir (together with M. Sojstrom and R. Olsson from MidSeden University), of Davi Freitas (together with I. Tabus from Tampere Univ.), of K. Gu (together with T. Maugey from Inria and S. Knorr from Technical Univ. Berlin), and of A. Atalay Appak (together with H. Caglayan and E. Sahim from Tampere University). These PhDs are double degrees in the framework of the European Marie Curie project Plenoptima.
- T. Maugey is supervising the PhD thesis of Tom Bachard and Tom Bordin (University of Rennes),
- T. Maugey and A. Roumy are co-supervising the PhD thesis of Reda Kaafarani, and Esteban Pesnel in the context of the Cifre contract with MediaKind, and the PhD thesis of Remi Piau in the context of the CominLabs CoLearn contract.
- A. Roumy has been supervising the PhD thesis of N. Charpenay (ENS-Paris Saclay doctoral grant), together with M. Le Treust (Ermine team, Irisa/Inria Center of the University of Rennes).
- A. Roumy is supervising the PhD thesis of C. Petit in collaboration with N. Keriven and T. Maugey.
- N. Keriven has supervised the PhD thesis of H. Ghanem with S. Vaiter (CNRS, LJAD, Nice) and J. Salmon (PU Univ. Montpellier).
- N. Keriven is supervising the PhD thesis of M. Cordonnier with S. Vaiter (CNRS, LJAD, Nice) and N. Tremblay (CNRS, GIPSA-lab, Grenoble).
- N. Keriven is supervising the PhD thesis of M. Gjorgjevski with S. Barthelmé (CNRS, GIPSA-lab, Grenoble) and Y. de Castro (Pr Centrale Lyon).
- N. Keriven has supervised the internship of A. Joly.
10.2.3 Juries
A. Roumy was rapporteur of the PhDs of
- M. Milovanovic, Institut Polytechnique de Paris, July 2023.
- Y. Sun, Univ. Paris-Saclay, Dec. 2023.
and chair of the PhD jury of
- T. Dardouri, Univ. Paris-Sorbonne, Feb. 2023.
T. Maugey was member of the PhD jury of S. Lingadahalli Ravi, IETR, Rennes, Dec. 2023.
10.3 Popularization
10.3.1 Internal or external Inria responsibilities
- T. Maugey is Scientific mediation officer in the scientific mediation team of Inria centre at Rennes Universiy.
11 Scientific production
11.1 Major publications
- 1 articleLight Field Super-Resolution using a Low-Rank Prior and Deep Convolutional Neural Networks.IEEE Transactions on Pattern Analysis and Machine Intelligence2019, 1-15HALDOI
- 2 articleLight Field Compression with Homography-based Low Rank Approximation.IEEE Journal of Selected Topics in Signal Processing2017HALDOI
- 3 articleA Fourier Disparity Layer representation for Light Fields.IEEE Transactions on Image ProcessingMay 2019, 5740 - 5753HALDOI
- 4 articleFine granularity access in interactive compression of 360-degree images based on rate-adaptive channel codes.IEEE Transactions on Multimedia2020HALDOI
- 5 articleOptimal Reference Selection for Random Access in Predictive Coding Schemes.IEEE Transactions on Communications6892020, 5819-5833HALDOI
- 6 articleGeometry-Aware Graph Transforms for Light Field Compact Representation.IEEE Transactions on Image ProcessingAugust 2019, 1-15HALDOI
11.2 Publications of the year
International journals
International peer-reviewed conferences
National peer-reviewed Conferences
Conferences without proceedings
Doctoral dissertations and habilitation theses
Reports & preprints
Other scientific publications

