2023Activity reportProject-TeamTOCCATA
RNSR: 201221053L- Research center Inria Saclay Centre at Université Paris-Saclay
- In partnership with:CNRS, Université Paris-Saclay
- Team name: Certified Programs, Certified Tools, Certified Floating-Point Computations
- In collaboration with:Laboratoire de Méthodes Formelles
- Domain:Algorithmics, Programming, Software and Architecture
- Theme:Proofs and Verification
Keywords
Computer Science and Digital Science
- A2.1.1. Semantics of programming languages
- A2.1.4. Functional programming
- A2.1.6. Concurrent programming
- A2.1.10. Domain-specific languages
- A2.1.11. Proof languages
- A2.4.2. Model-checking
- A2.4.3. Proofs
- A6.2.1. Numerical analysis of PDE and ODE
- A7.2. Logic in Computer Science
- A7.2.1. Decision procedures
- A7.2.2. Automated Theorem Proving
- A7.2.3. Interactive Theorem Proving
- A7.2.4. Mechanized Formalization of Mathematics
- A8.10. Computer arithmetic
Other Research Topics and Application Domains
- B5.2.2. Railway
- B5.2.3. Aviation
- B5.2.4. Aerospace
- B6.1. Software industry
- B9.5.1. Computer science
- B9.5.2. Mathematics
1 Team members, visitors, external collaborators
Research Scientists
- Claude Marché [Team leader, INRIA, Senior Researcher, HDR]
- Sylvie Boldo [INRIA, Senior Researcher, HDR]
- Jean-Christophe Filliâtre [CNRS, Senior Researcher, HDR]
- Armaël Guéneau [INRIA, Researcher]
- Guillaume Melquiond [INRIA, Senior Researcher, HDR]
Faculty Members
- Sylvain Conchon [UNIV PARIS SACLAY, Professor, HDR]
- Micaela Mayero [Univ. Sorbonne-Paris-Nord, Associate Professor, from Sep 2023, On leave (délégation) , HDR]
- Andriy Paskevych [UNIV PARIS SACLAY, Associate Professor]
PhD Students
- Léo Andrès [OCamlPro, CIFRE]
- Xavier Denis [Université Paris-Saclay]
- Paul Geneau De Lamarlière [MERCE, CIFRE, from Mar 2023]
- Antoine Lanco [UNIV PARIS SACLAY, ATER, until Sep 2023]
- Josué Moreau [INRIA]
- Houda Mouhcine [INRIA]
- Clément Pascutto [Taridès, CIFRE, until May 2023]
- Paul Patault [Univ Paris-Saclay, from Sep 2023]
Technical Staff
- Paul Bonnot [INRIA, Engineer]
- Paul Geneau De Lamarlière [INRIA, Engineer, until Feb 2023]
- David Hamelin [INRIA, Engineer, from Nov 2023]
- Matteo Manighetti [INRIA, Engineer, from May 2023]
- Solène Moreau [INRIA, Engineer, until Feb 2023]
Interns and Apprentices
- Gabriel Desfrene [INRIA, Intern, from May 2023 until Jul 2023]
- Tom Hubrecht [ENS PARIS-SACLAY, Intern, from Mar 2023 until Jul 2023]
- Valeran Maytie [INRIA, Intern, from May 2023 until Jul 2023]
- Dominik Josef Stolz [UNIV PARIS SACLAY, Intern, from Mar 2023 until Jul 2023]
Administrative Assistant
- Joyce Soares Brito [INRIA]
Visiting Scientists
- Arnaud Golfouse [LMF, from Oct 2023]
- Raphaël Rieu-Helft [TrustInSoft, partly on leave (plan de relance France 2030)]
External Collaborators
- Thibaut Balabonski [Université Paris-Saclay, LMF]
- Jacques-Henri Jourdan [CNRS, LMF]
- Chantal Keller [Université Paris-Saclay, LMF]
2 Overall objectives
The general objective of the Toccata project is to promote formal specification and computer-assisted proof in the development of software that requires high assurance in terms of safety and correctness with respect to its intended behavior. Such safety-critical software appears in many application domains like transportation (e.g. aviation, aerospace, railway, automotive), communication (e.g. internet, smartphones), health devices, data management on clouds (confidentialty issues), etc. The number of tasks performed by software is quickly increasing, together with the number of lines of code involved. Given the need of high assurance of safety in the functional behavior of such applications, the need for automated (in the sense computer-assisted) methods and techniques to bring guarantee of safety became a major challenge. In the past and at present, the most widely used approach to check safety of software is to apply heavy test campaigns, which take a large part of the costs of software development. Yet these campaigns cannot ensure that all the bugs are caught, and remaining bugs may have catastrophic consequences.
Generally speaking, software verification approaches pursue three goals: (1) verification should be sound, in the sense that no bugs should be missed, (2) verification should not produce false alarms, or as few as possible, (3) it should be as automatic as possible. Reaching all three goals at the same time is a challenge. A large class of approaches emphasizes goals (2) and (3): testing, run-time verification, symbolic execution, model checking, etc. Static analysis, such as abstract interpretation, emphasizes goals (1) and (3). Deductive verification emphasizes (1) and (2). The Toccata project is mainly interested in exploring the deductive verification approach, although we also combine with the other techniques occasionally.
In the past decade, significant progress has been made in the domain of deductive program verification. This is emphasized by some success stories of application of these techniques on industrial-scale software. For example, the Atelier B system was used to develop part of the embedded software of the Paris metro line 14 41 and other railway-related systems; a formally proved C compiler was developed using the Coq proof assistant 61; the L4-verified project developed a formally verified micro-kernel with high security guarantees, using analysis tools on top of the Isabelle/HOL proof assistant 59. A bug in the JDK implementation of TimSort was discovered using the KeY environment 58 and a fixed version was proved sound. Another sign of recent progress is the emergence of deductive verification competitions (e.g. VerifyThis 42). Finally, recent trends in the industrial practice for development of critical software is to require more and more guarantees of safety, e.g. the DO-178C standard for developing avionics software adds to the former DO-178B the use of formal models and formal methods. It also emphasizes the need for certification of the analysis tools involved in the process.
3 Research program
Panorama of Deductive Verification
There are two main families of approaches for deductive verification. Methods in the first family build on top of mathematical proof assistants (e.g. Coq, Isabelle) in which both the model and the program are encoded; the proof that the program meets its specification is typically conducted in an interactive way using the underlying proof construction engine. Methods from the second family proceed by the design of standalone tools taking as input a program in a particular programming language (e.g. C, Java) specified with a dedicated annotation language (e.g. ACSL 40, JML 49) and automatically producing a set of mathematical formulas (the verification conditions) which are typically proved using automatic provers (e.g. Z3 63, Alt-Ergo 50, CVC5 39).
The first family of approaches usually offers a smaller Trusted Code Base (TCB) than the second, but also demands more work to perform the proofs (because of their interactive nature) and makes them less easy to adopt by industry. Moreover, they generally do not allow to directly analyze a program written in a mainstream programming language like Java or C. The second kind of approaches has benefited in the past years from the tremendous progress made in SAT and SMT solving techniques, allowing more impact on industrial practices, but suffers from a lower level of trust: in all parts of the proof chain (the model of the input programming language, the VC generator, the back-end automatic prover), potential errors may appear, compromising the guarantee offered. Moreover, while these approaches are applied to mainstream languages, they usually support only a subset of their features.
Overall Goals of the Toccata Project
One of our original skills is the ability to conduct proofs by using automatic provers and proof assistants at the same time, depending on the difficulty of the program, and specifically the difficulty of each particular verification condition. We thus believe that we are in a good position to propose a bridge between the two families of approaches of deductive verification presented above. Establishing this bridge is one of the goals of the Toccata project: we want to provide methods and tools for deductive program verification that can offer both a high amount of proof automation and a high guarantee of validity.
In industrial applications, numerical calculations are very common (e.g. control software in transportation). Typically they involve floating-point numbers. Some of the members of Toccata have an internationally recognized expertise on deductive program verification involving floating-point computations. Our past work includes a new approach for proving behavioral properties of numerical C programs using Frama-C/Jessie 35, various examples of applications of that approach 47, the use of the Gappa solver for proving numerical algorithms 54, an approach to take architectures and compilers into account when dealing with floating-point programs 48, 65. We also contributed to the Handbook of Floating-Point Arithmetic 64. A representative case study is the analysis and the proof of both the method error and the rounding error of a numerical analysis program solving the one-dimension acoustic wave equation 4544. Our experience led us to a conclusion that verification of numerical programs can benefit a lot from combining automatic and interactive theorem proving 46, 47, 56, 57. Verification of numerical programs is another main axis of Toccata.
Let us conclude with more general considerations: we want to keep on with general audience actions (see Section 11.3), and industrial transfer through sustained long-term collaboration with industrial partners (Section 4). Our scientific programme detailed below is structured into the following four axes.
- Foundations and spreading of deductive program verification;
- Reasoning on mutable memory in program verification;
- Verification of Computer Arithmetic;
- Spreading Formal Proofs.
3.1 Foundations and spreading of deductive program verification
This axis covers the fundational studies we pursue regarding deductive verification. A non-exhaustive list of subjects we want to address is as follows.
- The search for improved methods to generate verification conditions, relying for example on new calculi, on better notion of abstraction, or on automatic discovery of invariants.
- Uniform approaches to obtain correct-by-construction programs and libraries, in particular by automatic extraction of executable code (in OCaml, C, CakeML, etc.) from verified programs, and including innovative general methods like advanced ghost code, ghost monitoring, etc. A representative publication is the presentation of a new notion called ghost monitors 5.
- Improvement of automated reasoning techniques: methods dedicated to deductive verification, so as to improve proof automation; improved combination of interactive provers and fully automated ones, proof by reflection.
- Providing feedback in case of proof failures, e.g. based on generation of counterexamples, or symbolic execution.
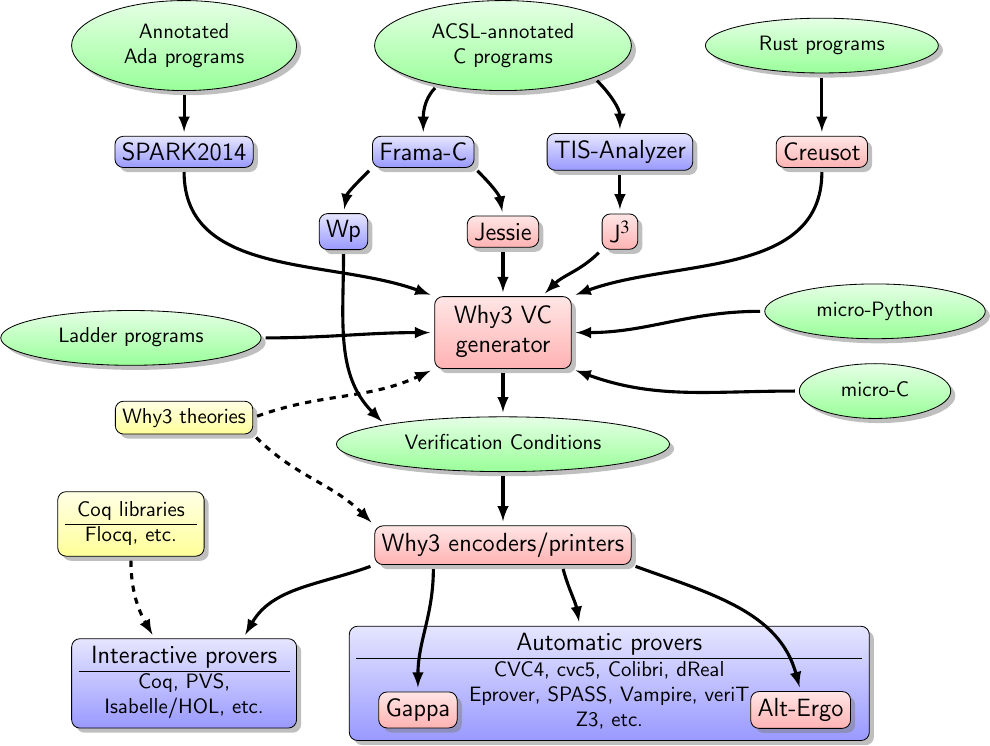
The Why3 ecosystem in 2023
A significant part of the work achieved in this axis is related to the Why3 toolbox and its ecosystem, displayed on Figure 1. The red background boxes represent tools that we develop ourselves, whereas blue background ones are developed by others. SPARK2014 is developed by AdaCore. Frama-C and Wp are developed by CEA-list and directly produce logical formulas to be passed to provers. TIS-Analyzer is developed by TrustInSoft and J is a collaboration between TrustInSoft and us. We develop the frontends micro-C and micro-Python mainly for teaching purpose. The front-end for Ladder programs is a software developed internally by MERCE. Yellow background boxes represent libraries of specifications of logic datatypes with their logical properties. A representative publication is an article on abstraction and genericity features of Why3 8.
3.2 Reasoning on mutable memory in program verification
This axis concerns specifically the techniques for reasoning on programs where memory aliasing is the central issue. It covers the methods based on type-based alias analysis and related memory models, on specific program logics such as separation logics, and extended model-checking. It concerns the application on analysis of C or C++ codes, on Ada codes involving pointers, but also concurrent programs in general. The main topics are:
- The study of advanced type systems dedicated to verification, for controlling aliasing, and their use for obtaining easier-to-prove verification conditions. Modern typing systems in the style of Rust, involving ownership and borrowing, are considered. A representation publication is a paper 10 on the semantic foundation of the verification of Rust programs.
- The design of front-ends of Why3 for the proofs of programs where aliasing cannot be fully controlled statically, via adequate memory models, aiming in particular at extraction to C; and also for concurrent programs.
- The continuation of fruitful work on concurrent parameterized systems, and its corresponding specific SMT-based model-checking. A reference publication is 6.
3.3 Verification of Computer Arithmetic
This axis, which bridges the domains of computer arithmetic and of formal verification, is a major originality of Toccata. The main topics are as follows.
- We are studying the fundamental blocks of formalizing floating-point computations, algorithms, and error analysis.
- A significant effort is dedicated to verification of numerical programs written in mainstream languages such as C or Ada. This involves combining specifications in real numbers and computation in floating-point, and underlying automated reasoning techniques with floating-point numbers and real numbers. We also contributed to the automation of reasoning on floating-point numbers 7.
- Related to the formalization of mathematics, we aim at verifying numerical analysis programs, in particular numerical schemes for solving partial differential equations. A representative publication is a paper on the formalization of Lebesgue integration 3 and a paper on certified approximations of integrals 9.
Boldo and Melquiond are authors of a reference book 4 on the formal verification of numerical programs.
3.4 Spreading Formal Proofs
The general goal of this axis, which was a new one proposed in 2019, was to encourage spreading of deductive verification through actions showing how our methods and tools can be used on programs that we develop ourselves. Since this axis is dedicated to applications in a general manner, positioning barely makes sense since a vast majority of research groups in computer science in the world would claim to conduct case studies and large-scale applications.
Representative of these significant case studies are the automated analysis of Debian packages installation 1 and the automated analysis of Ladder programs 2.
4 Application domains
4.1 Industrial Transfer Actions
The application domains we target involve safety-critical software, that is where a high-level guarantee of soundness of functional execution of the software is wanted. Currently our industrial collaborations or impact mainly belong to the domain of transportation: aerospace, aviation, railway, automotive.
-
Transfer to the community of Atelier B
in the context of the FUI project LCHIP, we investigated the use of Why3 and Alt-Ergo as an alternative back-end for checking proof obligations generated by Atelier B, whose main applications are railroad-related.
-
ProofInUse-AdaCore collaboration: transfer to the community of
Ada development
Since the creation of the ProofInUse joint lab in 2014, with AdaCore company, we have a growing impact on the community of industrial development of safety-critical applications written in Ada. See that web page for a an overview of AdaCore's customer projects, in particular those involving the use of the SPARK Pro tool set. This impact involves both the use of Why3 for generating VCs on Ada source codes, and the use of Alt-Ergo for performing proofs of those VCs. This action allowed AdaCore company to get new customers, in particular the domains of application of deductive formal verification are from the historical domain of aerospace (e.g. this link or this link) but went beyond: application in automotive (e.g. Denso, Toyata), medical and security (e.g. Nvidia). A joint publication of Nvidia and AdaCore 34 in 2023 exposes, with their own words, the benefit of using high level verification for securing Nvidia chips.
-
ProofInUse-TrustInSoft collaboration
In 2017 we started to collaborate with the TrustInSoft company for the verification of C and C++ codes. We started with a CIFRE thesis funding, which explored the use of Why3 to design verified and reusable C libraries 68, and then with a bilateral contract towards the design of the J plugin in TIS-Analyzer, bringing deductive verification techniques in this platfrom, including counterexamples when proofs fail. The impact on TrustInSoft customers is not yet easily identifiable; it will hopefully increase in particular in the context of the new project Décysif led by TrustInSoft.
-
ProofInUse-MERCE collaboration
In 2019 we started to collaborate with Mitsubishi Electric R&D Centre Europe in Rennes, France. The R&D programme is two-fold: first the verification of Ladder programs for PLCs, second the verification of numerical C codes. MERCE has now a mature platform for Ladder verification, which has yet to be made really usable by development teams. This work received the FMICS best paper award in 2021. The work of numerical programs is increasing in importance. We have preliminary results on log-sum-exp functions 30 and a CIFRE thesis started in 2023, aiming at designing better proof environments for verifying programs with complex numeric computations. A patent entitled Automatic implementation of formally-verified numerical programs has been filled in 2022 at EPO.
-
CIFRE thesis with Tarides
The CIFRE thesis of Clément Pascutto with Tarides, in 2020–2023, brought mature tooling for verifying function contracts and invariants on OCaml at runtime. The resulting tool, ortac, efficiently addresses the problem of capturing prestates in order to evaluation function postconditions 55. Tarides continues the development of ortac and uses it on its own code base.
-
CIFRE thesis with OCamlPro
The CIFRE thesis of Léo Andrès with OCamlPro, in 2021–2024, targets the compilation of OCaml to WebAssembly (Wasm for short), as an alternative to its compilation to JavaScript. It requires some extensions to Wasm, such as Wasm-GC, and the thesis already confirmed the adequacy of such extensions 17. A by-product of the thesis is the implementation of a new, efficient interpreter for Wasm, owi.
Generally speaking, we believe that our increasing industrial impact is a representative success for our general goal of spreading deductive verification methods to a larger audience, and we are firmly engaged into continuing such kind of actions in the next years.
4.2 Other socio-economic impact
We believe our impact is not limited to industrial actions per se.
A first point is that during the years, the young students that we train, either as a PhD position or a temporary engineer positions, easily got positions in private companies. Indeed we believe we can say that we contributed to the creation of jobs in several companies.
Another important part of our social impact is our work with high school students. With new curricula including more computer science than ever before, it was important to provide good reference books. With this in mind, we have contributed three books aimed at high school and preparatory school students 37, 36, 38.
The impact is not limited to books: we also helped a teacher to design a lesson to learn the basic notions of program verification (say: loop invariants) using the Why3 tool (article IREMI). We are also part each year of stands at “Fête de la science” in November or special events towards girls. We also often go to (high) schools for presenting either our job or our research (except during the Covid pandemic).
The social impact in national education is finally made highly evident by our implication in the organization of the new agrégation d'informatique which is in charge to select and recruit the best high-level teachers for the new programmes.
5 Social and environmental responsibility
5.1 Footprint of research activities
Our research activities make use of standard computers for developing software and developing formal proofs. We have no use of specific large size computing resources. Though, we are making use of external services for continuous integration. A continuous integration methodology for mature software like Why3 is indeed mandatory for ensuring a safe software engineering process for maintenance and evolution. We make the necessary efforts to keep the energy consumption of such a continuous integration process as low as possible.
Ensuring the reproducibility of proofs in formal verification is essential. It is thus mandatory to replay such proofs regularly to make sure that our changes in our software do not loose existing proofs. For example, we need to make sure that the case studies in formal verification that we present in our gallery are reproducible. We also make the necessary efforts to keep the energy consumption for replaying proofs low, by doing it only when necessary.
As widely accepted nowadays, the major sources of environmental impact of research is travel to international conferences by plane, and renewal of electronic devices. The number of travels we made in 2022 remained very low with respect to previous years, of course because of the Covid pandemic, and the fact that many conferences were now proposed online participation. We intend to continue limiting the environmental impact of our travels. Concerning renewal of electronic devices, that is mainly laptops and monitors, we have always been careful on keeping them usable for as long time as possible.
5.2 Impact of research results
Our research results aims at improving the quality of software, in particular in mission-critical contexts. As such, making software safer is likely to reduce the necessity for maintenance operations and thus reducing energy costs.
Our efforts are mostly towards ensuring the safety of functional behavior of software, but we also increasingly consider the verification of their time or memory consumption. Reducing those would naturally induce a reduction in energy consumption.
Our research never involve any processing of personal data, and consequently we have no concern about preserving individual privacy, and no concern with respect to the RGPD (Règlement Général sur la Protection des Données).
Recently, S. Boldo was in the program committee of the first PROPL workshop (Programming for the Planet ) to see how we may help topics such as climate analysis, modelling, forecasting, policy, and diplomacy.
6 Highlights of the year
- S. Boldo and G. Melquiond, together with C. P. Jeannerod and J.-M. Muller, published a reference survey (86 pages) on Floating-Point Arithmetic 12 in the journal Acta Numerica.
7 New software, platforms, open data
7.1 New software
7.1.1 Alt-Ergo
-
Name:
Automated theorem prover for software verification
-
Keywords:
Software Verification, Automated theorem proving
-
Functional Description:
Alt-Ergo is an automatic solver of formulas based on SMT technology. It is especially designed to prove mathematical formulas generated by program verification tools, such as Frama-C for C programs, or SPARK for Ada code. Initially developed in Toccata research team, Alt-Ergo's distribution and support are provided by OCamlPro since September 2013.
-
Release Contributions:
the "SAT solving" part can now be delegated to an external plugin, new experimental SAT solver based on mini-SAT, provided as a plugin. This solver is, in general, more efficient on ground problems, heuristics simplification in the default SAT solver and in the matching (instantiation) module, re-implementation of internal literals representation, improvement of theories combination architecture, rewriting some parts of the formulas module, bugfixes in records and numbers modules, new option "-no-Ematching" to perform matching without equality reasoning (i.e. without considering "equivalence classes"). This option is very useful for benchmarks coming from Atelier-B, two new experimental options: "-save-used-context" and "-replay-used-context". When the goal is proved valid, the first option allows to save the names of useful axioms into a ".used" file. The second one is used to replay the proof using only the axioms listed in the corresponding ".used" file. Note that the replay may fail because of the absence of necessary ground terms generated by useless axioms (that are not included in .used file) during the initial run.
- URL:
-
Contact:
Sylvain Conchon
-
Participants:
Alain Mebsout, Évelyne Contejean, Mohamed Iguernelala, Stéphane Lescuyer, Sylvain Conchon
-
Partner:
OCamlPro
7.1.2 CoqInterval
-
Name:
Interval package for Coq
-
Keywords:
Interval arithmetic, Coq
-
Functional Description:
CoqInterval is a library for the proof assistant Coq.
It provides several tactics for proving theorems on enclosures of real-valued expressions. The proofs are performed by an interval kernel which relies on a computable formalization of floating-point arithmetic in Coq.
The Marelle team developed a formalization of rigorous polynomial approximation using Taylor models in Coq. In 2014, this library has been included in CoqInterval.
- URL:
- Publications:
-
Contact:
Guillaume Melquiond
-
Participants:
Assia Mahboubi, Érik Martin-Dorel, Guillaume Melquiond, Jean-Michel Muller, Laurence Rideau, Laurent Théry, Micaela Mayero, Mioara Joldes, Nicolas Brisebarre, Thomas Sibut-Pinote
7.1.3 Coquelicot
-
Name:
The Coquelicot library for real analysis in Coq
-
Keywords:
Coq, Real analysis
-
Functional Description:
Coquelicot is library aimed for supporting real analysis in the Coq proof assistant. It is designed with three principles in mind. The first is the user-friendliness, achieved by implementing methods of automation, but also by avoiding dependent types in order to ease the stating and readability of theorems. This latter part was achieved by defining total function for basic operators, such as limits or integrals. The second principle is the comprehensiveness of the library. By experimenting on several applications, we ensured that the available theorems are enough to cover most cases. We also wanted to be able to extend our library towards more generic settings, such as complex analysis or Euclidean spaces. The third principle is for the Coquelicot library to be a conservative extension of the Coq standard library, so that it can be easily combined with existing developments based on the standard library.
- URL:
-
Contact:
Sylvie Boldo
-
Participants:
Catherine Lelay, Guillaume Melquiond, Sylvie Boldo
7.1.4 Cubicle
-
Name:
The Cubicle model checker modulo theories
-
Keywords:
Model Checking, Software Verification
-
Functional Description:
Cubicle is an open source model checker for verifying safety properties of array-based systems, which corresponds to a syntactically restricted class of parametrized transition systems with states represented as arrays indexed by an arbitrary number of processes. Cache coherence protocols and mutual exclusion algorithms are typical examples of such systems.
- URL:
-
Contact:
Sylvain Conchon
-
Participants:
Alain Mebsout, Sylvain Conchon
7.1.5 Flocq
-
Name:
The Flocq formalization of floating-point arithmetic for the Coq proof assistant
-
Keywords:
Floating-point, Arithmetic code, Coq
-
Functional Description:
The Flocq library for the Coq proof assistant is a comprehensive formalization of floating-point arithmetic: core definitions, axiomatic and computational rounding operations, high-level properties. It provides a framework for developers to formally verify numerical applications.
Flocq is currently used by the CompCert verified compiler to support floating-point computations.
- URL:
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Guillaume Melquiond, Pierre Roux, Sylvie Boldo
7.1.6 Gappa
-
Name:
The Gappa tool for automated proofs of arithmetic properties
-
Keywords:
Floating-point, Arithmetic code, Software Verification, Constraint solving
-
Functional Description:
Gappa is a tool intended to help formally verifying numerical programs dealing with floating-point or fixed-point arithmetic. It has been used to write robust floating-point filters for CGAL and it is used to verify elementary functions in CRlibm. While Gappa is intended to be used directly, it can also act as a backend prover for the Why3 software verification plateform or as an automatic tactic for the Coq proof assistant.
- URL:
- Publications:
-
Contact:
Guillaume Melquiond
-
Participant:
Guillaume Melquiond
7.1.7 Why3
-
Name:
The Why3 environment for deductive verification
-
Keywords:
Formal methods, Trusted software, Software Verification, Deductive program verification
-
Functional Description:
Why3 is an environment for deductive program verification. It provides a rich language for specification and programming, called WhyML, and relies on external theorem provers, both automated and interactive, to discharge verification conditions. Why3 comes with a standard library of logical theories (integer and real arithmetic, Boolean operations, sets and maps, etc.) and basic programming data structures (arrays, queues, hash tables, etc.). A user can write WhyML programs directly and get correct-by-construction OCaml programs through an automated extraction mechanism. WhyML is also used as an intermediate language for the verification of C, Java, or Ada programs.
- URL:
-
Contact:
Claude Marche
-
Participants:
Andriy Paskevych, Claude Marche, François Bobot, Guillaume Melquiond, Jean-Christophe Filliâtre, Levs Gondelmans, Martin Clochard
-
Partners:
CNRS, Université Paris-Sud
7.1.8 Coq
-
Name:
The Coq Proof Assistant
-
Keywords:
Proof, Certification, Formalisation
-
Scientific Description:
Coq is an interactive proof assistant based on the Calculus of (Co-)Inductive Constructions, extended with universe polymorphism. This type theory features inductive and co-inductive families, an impredicative sort and a hierarchy of predicative universes, making it a very expressive logic. The calculus allows to formalize both general mathematics and computer programs, ranging from theories of finite structures to abstract algebra and categories to programming language metatheory and compiler verification. Coq is organised as a (relatively small) kernel including efficient conversion tests on which are built a set of higher-level layers: a powerful proof engine and unification algorithm, various tactics/decision procedures, a transactional document model and, at the very top an integrated development environment (IDE).
-
Functional Description:
Coq provides both a dependently-typed functional programming language and a logical formalism, which, altogether, support the formalisation of mathematical theories and the specification and certification of properties of programs. Coq also provides a large and extensible set of automatic or semi-automatic proof methods. Coq's programs are extractible to OCaml, Haskell, Scheme, ...
-
Release Contributions:
An overview of the new features and changes, along with the full list of contributors is available at https://coq.inria.fr/refman/changes.html#version-8-18 .
-
News of the Year:
Coq version 8.16 integrates changes to the Coq kernel and performance improvements along with a few new features. See the detailed changes at https://coq.inria.fr/refman/changes.html#version-8-16 for an overview of the new features and changes, along with the full list of contributors.
- URL:
-
Contact:
Matthieu Sozeau
-
Participants:
Yves Bertot, Frédéric Besson, Tej Chajed, Cyril Cohen, Pierre Corbineau, Pierre Courtieu, Maxime Dénès, Jim Fehrle, Julien Forest, Emilio Jesús Gallego Arias, Gaëtan Gilbert, Georges Gonthier, Benjamin Grégoire, Jason Gross, Hugo Herbelin, Vincent Laporte, Olivier Laurent, Assia Mahboubi, Kenji Maillard, Érik Martin-Dorel, Guillaume Melquiond, Pierre-Marie Pedrot, Clément Pit-Claudel, Kazuhiko Sakaguchi, Vincent Semeria, Michael Soegtrop, Arnaud Spiwack, Matthieu Sozeau, Enrico Tassi, Laurent Théry, Anton Trunov, Li-Yao Xia, Theo Zimmermann
-
Partners:
CNRS, Université Paris-Sud, ENS Lyon, Université Paris-Diderot
7.1.9 creusot
-
Name:
Creusot
-
Keywords:
Rust, Specification language, Deductive program verification
-
Functional Description:
Creusot is a tool for deductive verification of Rust code. It allows you to annotate your code with specifications, invariants and assertions and then verify them formally and automatically, proving, mathematically, that your code satisfies your specifications.
Creusot works by translating Rust code to WhyML, the verification and specification language of Why3. Users can then leverage the full power of Why3 to (semi)-automatically discharge the verification conditions.
-
Release Contributions:
This is the first version, providing the main process to go from a Rust program annotated with Pearlite specifications to a set of verifications conditions to be discharged by external SMT solvers.
- URL:
- Publications:
-
Contact:
Xavier Denis
-
Participants:
Xavier Denis, Jacques-Henri Jourdan, Claude Marche
-
Partners:
Université Paris-Saclay, CNRS
7.1.10 coq-num-analysis
-
Name:
Numerical analysis Coq library
-
Keywords:
Coq, Numerical analysis, Real analysis
-
Scientific Description:
These Coq developments are based on the Coquelicot library for real analysis. Version 1.0 includes the formalization and proof of: (1) the Lax-Milgram theorem, including results from linear algebra, geometry, functional analysis and Hilbert spaces, (2) the Lebesgue integral, including large parts of the measure theory,the building of the Lebesgue measure on real numbers, integration of nonnegative measurable functions with the Beppo Levi (monotone convergence) theorem, Fatou's lemma, the Tonelli theorem, and the Bochner integral with the dominated convergence theorem.
-
Functional Description:
Formal developments and proofs in Coq of numerical analysis problems. The current long-term goal is to formally prove parts of a C++ library implementing the Finite Element Method.
-
News of the Year:
The formalization in Coq of simplicial Lagrange finite elements is almost complete. This include the formalizations of the definitions and main properties of monomials, their representation using multi-indices, Lagrange polynomials, the vector space of polynomials of given maximum degree (about 6 kloc). This also includes algebraic complements on the formalization of the definitions and main properties of operators on finite families of any type, the specific cases of abelian monoids (sum), vector spaces (linear combination), and affine spaces (affine combination, barycenter, affine mapping), sub-algebraic structures, and basics of finite dimension linear algebra (about 22 kloc). A new version (2.0) of the opam package will be available soon, and a paper will follow.
We have also contributed to the Coquelicot library by adding the algebraic structure of abelian monoid, which is now the base of the hierarchy of canonical structures of the library.
- URL:
- Publications:
-
Contact:
Sylvie Boldo
-
Participants:
Sylvie Boldo, François Clement, Micaela Mayero, Vincent Martin, Stéphane Aubry, Florian Faissole, Houda Mouhcine, Louise Leclerc
-
Partners:
LIPN (Laboratoire d'Informatique de l'Université Paris Nord), LMAC (Laboratoire de Mathématiques Appliquées de Compiègne)
7.2 Open data
The use of data in the Toccata is quite simple and perfectly open. First of all, we never make use of any personal data, so we have no issue in being conforming to European rules such as RGPD.
Our data is in fact mainly made of programs, but also and importantly equipped with formal specifications. These specifications are often completed with additional formal annotations in the code itself so as the make the code automatically provable conforming to its specifications. The most important kind of such internal annotations are the loop invariants. Exposing such loop invariants is always a crucial information to make the proofs automatic and reproducible. One may even say that loop invariants are the central arguments for the correctness of an algorithm. Given the importance of such data for reproducibility of proofs, we decided to make it available openly. This is why we decided to build a gallery of verified programs that is augmented regularly.
Other similar anontated programs are part of the tests suites of our tools, and are typically rechecked regularly in continuous integration processes. This for example the case for Why3 and Creusot. Such a practice is crucial to maintain the reproducibility of proofs in a long term, when the tools themselves evolve.
8 New results
8.1 Foundations and Spreading of Deductive Program Verification
Participants: Andrei Paskevich, Antoine Lanco, Claude Marché, Clément Pascutto, Guillaume Melquiond, Jean-Christophe Filliâtre, Léo Andrès, Quentin Garchery, Solène Moreau, Sylvain Conchon, Xavier Denis.
Programming language semantics
A representative fundational work is those of Balabonski, Lanco, and Melquiond who devised a call-by-need lambda-calculus enabling strong reduction (i.e. reduction inside the body of abstractions) and guarantees that arguments are only evaluated if needed and at most once 1160. This calculus uses explicit substitutions and subsumes the existing strong-call-by-need strategy, but allows for more reduction sequences, and often shorter ones, while preserving the neededness. The calculus is strongly normalizing. Moreover, by adding some restrictions to it, the calculus gains the diamond property and only performs reduction sequences of minimal length, which makes it systematically better than the existing strategies. The Abella proof assistant has been used to formalize part of this calculus.
Improving Verification Condition Generation
Continuation-passing style allows us to devise an extremely economical abstract syntax for a generic algorithmic language. This syntax is flexible enough to naturally express conditionals, loops, (higher-order) function calls, and exception handling. It is type-agnostic and state-agnostic, which means that we can combine it with a wide range of type and effect systems. Paskevich 31 shows how programs written in the continuation-passing style can be augmented in a natural way with specification annotations, ghost code, and side-effect discipline. He defines the rules of verification condition generation for this syntax, and shows that the resulting formulas are nearly identical to what traditional approaches, like the weakest precondition calculus, produce for the equivalent algorithmic constructions. This amounts to a minimalistic yet versatile abstract syntax for annotated programs for which one can compute verification conditions without sacrificing their size, legibility, and amenability to automated proof, compared to more traditional methods. This makes it an excellent candidate for internal code representation in program verification tools, a subject of the on-going PhD thesis of P. Patault.
Inference of invariants
The discovery of invariants is another important topic. A fully automatic generation of invariants was studied in collaboration with an industrial partner: we devised an original abstract interpretation based approach using a domain of parametrized binary decision diagrams 27.
Formal Specification Language for C code
ACSL, short for ANSI/ISO C Specification Language, is meant to express precisely and unambiguously the expected behavior of a piece of C code. It plays a central role in Frama-C, as nearly all plug-ins eventually manipulate ACSL specifications, either to generate properties that are to be verified, or to assess that the code is conforming to these specifications. It is thus very important to have a clear view of ACSL's semantics in order to be sure that what you check with Frama-C is really what you mean. Marché contributed to a chapter 28 of the Frama-C book, describing the language in an agnostic way, independently of the various verification plug-ins that are implemented in the Frama-C platform. It contains many examples and exercises that introduce the main features of the language and insists on the most common pitfalls that users, even experienced ones, may encounter.
8.2 Reasoning on mutable memory in program verification
Participants: Andrei Paskevich, Armaël Guéneau, Claude Marché, Clément Pascutto, Guillaume Melquiond, Jean-Christophe Filliâtre, Léo Andrès, Sylvain Conchon, Xavier Denis.
Verification of Rust programs
One of the major success of Toccata during the last years is represented by the results obtained concerning the verification of Rust programs. Rust is a fairly recent programming language for system programming, bringing static guarantees of memory safety through a strong ownership policy. This feature opens promising advances for deductive verification of Rust code. The project underlying the PhD thesis of Denis 51, supervised by Jourdan and Marché, is to propose techniques for the verification of Rust program, using a translation to a purely-functional language. The challenge of this translation is the handling of mutable borrows: pointers which control of aliasing in a region of memory. To overcome this, we used a technique inspired by prophecy variables to predict the final values of borrows 52. This method is implemented in a standalone tool called Creusot 53. The specification language of Creusot features the notion of prophecy mentioned above, which is central for the specification of behavior of programs performing memory mutation. Prophecies also permit efficient automated reasoning for verifying about such programs. Moreover, Rust provides advanced abstraction features based on a notion of traits, extensively used in the standard library and in user code. The support for traits is another main feature of Creusot, because it is at the heart of its approach, in particular for providing complex abstraction of the functional behavior of programs 53. An important step to take further in the applicability of Creusot on a wide variety of Rust code is to support iterators, which are ubiquitous and in fact idiomatic in Rust programming (for example, every for loop is in fact internally desugared into an iterator). Denis and Jourdan 20 proposed a new approach to simplify the specifications of Rust code in presence of iterators, and to also make the proofs more automatic.
Reasoning on Memory Separation using Arithmetic
Paskevich and Filliâtre 26 proposed an approach that helps to improve automation of proofs for certain classes of pointer-manipulating programs. It consists in mapping a recursive data structure onto a numerical domain, in such a way that ownership and separation properties can be expressed in terms of simple arithmetic inequalities. In addition to making the proof simpler, this provides for a clearer and more natural specification.
Reasoning on Resources
Ownership can also be used to reason about resources other than program memory. Guéneau, Jourdan et al. 24 present formal reasoning rules for verifying amortized complexity bounds in a language with thunks. Thunks can be used to construct persistent data structures with good amortized complexity, by suspending expensive computations and memoizing their result. Based on the notion of time credits and debits, this work presents a complete machine-checked reconstruction of Okasaki's reasoning rules on thunks in a rich separation logic with time credits, and demonstrates their applicability by verifying several of Okasaki's data structures.
Ownership and Well-Bracketedness
Ability to reason about ownership is also fertile ground for designing reasoning principles that capture powerful semantic properties of programs. In particular, Guéneau et al. 25 show that it is possible to capture well-bracketedness in a Hoare-style program logic based on separation logic, providing proof rules to show correctness of well-bracketed programs both directly and also through defining unary and binary logical relations models based on this program logic.
Multi-language verification
Most of the existing verification tools and systems focus on programs that are written in a single programming language. In practice, however, programs are often composed of components written in different programming languages, interacting through a foreign function interface (FFI). Guéneau et al. 22 develop a novel multi-language program verification system, dubbed Melocoton, for reasoning about OCaml, C, and their interactions through the OCaml FFI. Melocoton consists of the first formal semantics of (a large subset of) the OCaml FFI—previously only described in prose in the OCaml manual—as well as the first program logic to reason about the interactions of programs components written in OCaml and C. The Melocoton program logic is based on separation logic and expressive enough to express fine-grained transfers of ownership between the different languages. It has been fully mechanized in Coq on top of the Iris separation logic framework.
Capability Machines
A capability machine is a type of CPU allowing fine-grained privilege separation using capabilities, machine words that represent certain kinds of authority. Guéneau et al. 13 present a mathematical model and accompanying proof methods that can be used for formal verification of functional correctness of programs running on a capability machine, even when they invoke and are invoked by unknown (and possibly malicious) code. They use a program logic called Cerise for reasoning about known code, and an associated logical relation, for reasoning about unknown code. The logical relation formally captures the capability safety guarantees provided by the capability machine. The Cerise program logic, logical relation, and all the examples considered in the paper have been mechanized using the Iris program logic framework in the Coq proof assistant. In subsequent work, they show that this approach enables the formal verification of full-system security properties under multiple attacker models: different security objectives of the full system can be verified under a different choice of trust boundary (i.e. under a different attacker model) 69. The proposed verification approach is modular, and is robust: code outside the trust boundary for a given security objective can be arbitrary, unverified attacker-provided code.
Distributed Programs and Concurrency
Our work regarding concurrent programs is mostly represented by new methods based on model-checking, and implemented in the Cubicle tool. The Model Checking Modulo Theories (MCMT) framework is a powerful model checking technique for verifying safety properties of parameterized transition systems. In MCMT, logical formulas are used to represent both transitions and sets of states and safety properties are verified by an SMT-based backward reachability analysis. To be fully automated, the class of formulas handled in MCMT is restricted to cubes, i.e. existentially quantified conjunction of literals. While being very expressive, cubes cannot define properties with a global termination condition, usually described by a universally quantified formula. Conchon and Korneva 19 presented the Cubicle Fuzzy Loop (CFL), a fuzzing-based extension for Cubicle. To prove safety, Cubicle generates invariants, making use of forward exploration strategies like BFS or DFS on finite model instances. However, these standard algorithms are quickly faced with the state explosion problem due to Cubicle’s purely nondeterministic semantics. This causes them to struggle at discovering critical states, hindering invariant generation. CFL replaces this approach with a powerful DFS-like algorithm inspired by fuzzing. Cubicle’s purely nondeterministic execution loop is modified to provide feedback on newly discovered states and visited transitions. This feedback is used by CFL to construct schedulers that guide the model exploration. Not only does this provide Cubicle with a bigger variety of states for generating invariants, it also quickly identifies unsafe models. As a bonus, it adds testing capabilities to Cubicle, such as the ability to detect deadlocks. The first experiments yielded promising results. CFL effectively allows Cubicle to generate crucial invariants, useful to handle hierarchical systems, while also being able to trap bad states and deadlocks in hard-to-reach areas of such models.
8.3 Verification of Computer Arithmetic
Participants: Claude Marché, Guillaume Melquiond, Houda Mouhcine, Josué Moreau, Paul Bonnot, Paul Geneau de Lamarlière, Sylvie Boldo.
Error analysis for Logarithm-Sum-Exponential
We have a long tradition of study of various subtle algorithms involving numerical computations, and verified properties regarding accuracy in particular when using floating-point numbers. A set of numerical programs that we studied this year is related to combination of exponential and logarithm functions, Bonnot et al. 30 provide certified bounds on the accuracy of the log-sum-exp function known in the context of Machine Learning 62. Writing a formal proof offers the highest possible confidence in the correctness of a mathematical library. This comes at a large cost though, since formal proofs require taking into account all the details, even the seemingly insignificant ones, which makes them tedious to write. This issue is compounded by the fact that the objects whose properties we need to verify (floating-point numbers) are not the ones we would like to reason about (real numbers and integers). Geneau, Melquiond and Faissole 21 explore some ways of reducing the overhead of formal proofs in the setting of mathematical libraries, so as to let the user focus on the details that really matter.
Automating the reasoning on Floating-Point Numbers and Real Numbers
Performing a formal verification inside a proof system such as Coq might be a costly endeavor. In some cases, it might be much more efficient to turn the whole process of proof generation and proof checking into the evaluation of a boolean formula, accompanied with a proof that, if this formula evaluates to true, then the original property holds. This approach has long been used for proofs that involve computations on large integers. Martin-Dorel, Melquiond and Roux 14 have shown that computational reflection can also be achieved using floating-point arithmetic, despite the inherent round-off errors, thus leveraging the large computing power of the floating-point units for formal proofs.
Survey on Floating-Point Arithmetic
Boldo et al. published a survey on floating-point arithmetic 12 as an open-access journal paper in Acta Numerica in order to spread the knowledge on computer arithmetic.
Formalization of Mathematics
The correctness of programs solving partial differential equations may rely on mathematics yet unformalized, such as Sobolev spaces. Boldo et al. 43 therefore formalized the mathematical concept of Lebesgue integration and the associated results in Coq (-algebras, measures, simple functions, and integration of non-negative measurable functions, up to the full formal proofs of the Beppo Levi Theorem and Fatou's Lemma). Boldo et al. 29, 18 extended this formalization with Tonelli's theorem, stating that the (double) integral of a nonnegative measurable function of two variables can be computed by iterated integrals, and allowing to switch the order of integration.
Manifest Termination
In formal systems combining dependent types and inductive types, such as Coq, non-terminating programs are frowned upon. They can indeed be made to return impossible results, thus endangering the consistency of the system, although the transient usage of a non-terminating Y combinator, typically for searching witnesses, is safe. To avoid this issue, the definition of a recursive function is allowed only if one of its arguments is of an inductive type and any recursive call is performed on a syntactically smaller argument. If there is no such argument, the user has to artificially add one, e.g., an accessibility property. Free monads can still be used to address general recursion and elegant methods make possible to extract partial functions from sophisticated recursive schemes. The latter yet rely on an inductive characterization of the domain of a function, and of its computational graph, which in turn might require a substantial effort of specification and proof. This leads to a rather frustrating situation when computations are involved. Indeed, the user first has to formally prove that the function will terminate, then the computation can be performed, and finally a result is obtained (assuming the user waited long enough). But since the computation did terminate, what was the point of proving that it would terminate? Mahboubi and Melquiond 23 investigated how users of proof assistants based on variants of the Calculus of Inductive Constructions could benefit from manifestly terminating computations.
8.4 Spreading Formal Proofs
Participants: Andrei Paskevich, Antoine Lanco, Armaël Guéneau, Claude Marché, Clément Pascutto, Guillaume Melquiond, Houda Mouhcine, Jean-Christophe Filliâtre, Josué Moreau, Léo Andrès, Paul Bonnot, Paul Geneau de Lamarlière, Solène Moreau, Sylvain Conchon, Sylvie Boldo, Xavier Denis, Yacine El Haddad.
Specifying, Testing, and Verifying OCaml programs
Our work on OCaml programs is not limited to purely static verification: we worked on runtime assertion checking for OCaml. In behavioural specifications of imperative languages, postconditions may refer to the prestate of the function, usually with an old operator. Therefore, code performing runtime verification has to record prestate values required to evaluate the postconditions, typically by copying part of the memory state, which causes severe verification overhead, both in memory and CPU time. Filliâtre and Pascutto 55, 67 consider the problem of efficiently capturing prestates in the context of Ortac, a runtime assertion checking tool for OCaml. Their contribution is a postcondition transformation that reduces the subset of the prestate to copy. They formalize this transformation, and they provide proof that it is sound and improves the performance of the instrumented programs. They illustrate the benefits of this approach with a maze generator. Benchmarks show that unoptimized instrumentation is not practicable, while their transformation restores performances similar to the program without any runtime check.
Leveraging Formal Specifications to Generate Fuzzing Suites
When testing a library, developers typically first have to capture the semantics they want to check. They then write the code implementing these tests and find relevant test cases that expose possible misbehaviours. In this work, Osborne and Pascutto 66, 67 present a tool that automatically takes care of these last two steps by automatically generating fuzz testing suites from OCaml interfaces annotated with formal behavioral specifications. They also show some ongoing experiments on the capabilities and limitations of fuzzing applied to real-world libraries.
Compiling OCaml to WebAssembly
As part of his CIFRE PhD with OCamlPro, Léo Andrès formalizes a compilation scheme from OCaml to WebAssembly. This on-going work already validated several Wasm extensions 17. A by-product of the thesis is the implementation of a new, efficient interpreter for Wasm, owi. Léo collaborates with José Fragoso Santos and Filipe Marques (Universidade de Lisboa, Portugal), who are using owi for concolic execution of WebAssembly programs.
9 Bilateral contracts and grants with industry
We have bilateral contracts which are closely related to a joint effort called the ProofInUse consortium. The objective of ProofInUse is to provide verification tools, based on mathematical proof, to industry users. These tools are aimed at replacing or complementing the existing test activities, whilst reducing costs.
This consortium is a follow-up of the former LabCom ProofInUse between Toccata and the SME AdaCore, funded by the ANR programme “Laboratoires communs”, from April 2014 to March 2017.
9.1 ProofInUse-AdaCore Collaboration
Participants: Claude Marché [contact], Jean-Christophe Filliâtre, Andrei Paskevich, Guillaume Melquiond, Solène Moreau.
This collaboration is a joint effort of the Inria project-team Toccata and the AdaCore company which provides development tools for the Ada programming language. It is funded by a 5-year bilateral contract from Jan 2019 to Dec 2023.
The SME AdaCore is a software publisher specializing in providing software development tools for critical systems. A previous successful collaboration between Toccata and AdaCore enabled Why3 technology to be put into the heart of the AdaCore-developed SPARK technology.
The objective of ProofInUse-AdaCore is to significantly increase the capabilities and performances of the Spark/Ada verification environment proposed by AdaCore. It aims at integration of verification techniques at the state-of-the-art of academic research, via the generic environment Why3 for deductive program verification developed by Toccata.
9.2 ProofInUse-MERCE Collaboration
Participants: Claude Marché [contact], Guillaume Melquiond, Paul Bonnot, Paul Geneau de Lamarlière.
This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company Mitsubishi Electric R&D (MERCE) in Rennes. It is funded by a bilateral contract of 3 years and 6 months from Nov 2019 to April 2023.
MERCE has strong and recognized skills in the field of formal methods. In the industrial context of the Mitsubishi Electric Group, MERCE has acquired knowledge of the specific needs of the development processes and meets the needs of the group in different areas of application by providing automatic verification and demonstration tools adapted to the problems encountered.
The objective of ProofInUse-MERCE is to significantly improve on-going MERCE tools regarding the verification of Programmable Logic Controllers and also regarding the verification of numerical C codes.
9.3 ProofInUse-TrustInSoft Collaboration
Participants: Claude Marché [contact], Guillaume Melquiond, Raphaël Rieu-Helft, Paul Bonnot.
This bilateral contract is part of the ProofInUse effort. This collaboration joins efforts of the Inria project-team Toccata and the company TrustInSoft in Paris. It is funded by a bilateral contract of 24 months from Dec 2020 to Nov 2022.
TrustInSoft is an SME that offers the TIS-Analyzer environment for analysis of safety and security properties of source codes written in C and C++ languages. A version of TIS-Analyzer is available online, under the name TaaS (TrustInSoft as a Service).
The objective of ProofInUse-TrustInSoft is to integrate Deductive Verification in the platform TIS-Analyzer, under the form of a new plug-in called J-cube. One specific interest resides in the generation of counterexample to help the user in case of proof failure.
9.4 Action “Plan de relance” Toccata-TrustInSoft
Participants: Claude Marché [contact], Raphaël Rieu-Helft.
Toccata and the company TrustInSoft set up a research action in the context of the national “plan de relance”. It is funded for 24 months from January 2022 to December 2023. The funding covers the leave of R. Rieu-Helft for 80% time as an invited researcher in Toccata.
The objective of this action is to extend the ProofInUse-TrustInSoft collaboration towards two axes: a refinement of the J-cube memory model incorporating a static separation analysis, and the support of the C++ language.
9.5 CIFRE contract with Tarides company
Participants: Jean-Christophe Filliâtre [contact], Clément Pascutto.
Clément Pascutto started a CIFRE PhD in June 2020, under the supervision of Jean-Christophe Filliâtre (at Toccata) and Thomas Gazagnaire (at Tarides). The subject of the PhD is the dynamic and deductive verification of OCaml programs and its application to distributed data structures.
9.6 CIFRE contract with OCamlPro company
Participants: Jean-Christophe Filliâtre [contact], Léo Andrès.
Léo Andrès started a CIFRE PhD in October 2021, under the supervision of Jean-Christophe Filliâtre (at Toccata) and Pierre Chambart and Vincent Laviron (at OCamlPro). The subject of the PhD is the design, formalization, and implementation of a garbage collector for WebAssembly.
10 Partnerships and cooperations
10.1 European initiatives
10.1.1 H2020 projects
EMC2, ERC Synergy project
EMC2 project on cordis.europa.eu
-
Title:
Extreme-scale Mathematically-based Computational Chemistry
-
Duration:
From September 1, 2019 to February 28, 2026
-
Partners:
- INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET AUTOMATIQUE (INRIA), France
- ECOLE NATIONALE DES PONTS ET CHAUSSEES (ENPC), France
- CENTRE NATIONAL DE LA RECHERCHE SCIENTIFIQUE CNRS (CNRS), France
- SORBONNE UNIVERSITE, France
-
Inria contact:
Laura GRIGORI (Alpines)
- Coordinator:
-
Summary:
Molecular simulation has become an instrumental tool in chemistry, condensed matter physics, molecular biology, materials science, and nanosciences. It will allow to propose de novo design of e.g. new drugs or materials provided that the efficiency of underlying software is accelerated by several orders of magnitude.
The ambition of the EMC2 project is to achieve scientific breakthroughs in this field by gathering the expertise of a multidisciplinary community at the interfaces of four disciplines: mathematics, chemistry, physics, and computer science. It is motivated by the twofold observation that, i) building upon our collaborative work, we have recently been able to gain efficiency factors of up to 3 orders of magnitude for polarizable molecular dynamics in solution of multi-million atom systems, but this is not enough since ii) even larger or more complex systems of major practical interest (such as solvated biosystems or molecules with strongly-correlated electrons) are currently mostly intractable in reasonable clock time. The only way to further improve the efficiency of the solvers, while preserving accuracy, is to develop physically and chemically sound models, mathematically certified and numerically efficient algorithms, and implement them in a robust and scalable way on various architectures (from standard academic or industrial clusters to emerging heterogeneous and exascale architectures).
EMC2 has no equivalent in the world: there is nowhere such a critical number of interdisciplinary researchers already collaborating with the required track records to address this challenge. Under the leadership of the 4 PIs, supported by highly recognized teams from three major institutions in the Paris area, EMC2 will develop disruptive methodological approaches and publicly available simulation tools, and apply them to challenging molecular systems. The project will strongly strengthen the local teams and their synergy enabling decisive progress in the field.
FRESCO, ERC Consolidator project
-
Title:
Fast and Reliable Symbolic Computation
-
Duration:
November 2021 – October 2026
-
Coordinator:
Assia Mahboubi
- Website
Using computers to formulate conjectures and consolidate proof steps pervades all mathematics fields, even the most abstract. Most computer proofs are produced by symbolic computations, using computer algebra systems. However, these systems suffer from severe, intrinsic flaws, rendering computational correction and verification challenging. The FRESCO project aims to shed light on whether computer algebra could be both reliable and fast. Researchers will disrupt the architecture of proof assistants, which serve as the best tools for representing mathematics in silico, enriching their programming features while preserving their compatibility with their logical foundations. They will also design novel mathematical software that should feature a high-level, performance-oriented programming environment for writing efficient code to boost computational mathematics.
10.2 National initiatives
10.2.1 ANR NuSCAP
Participants: Guillaume Melquiond [contact], Sylvie Boldo.
The last twenty years have seen the advent of computer-aided proofs in mathematics and this trend is getting more and more important. They request various levels of numerical safety, from fast and stable computations to formal proofs of the computations. Hovewer, the necessary tools and routines are usually ad hoc, sometimes unavailable, or inexistent. On a complementary perspective, numerical safety is also critical for complex guidance and control algorithms, in the context of increased satellite autonomy. We plan to design a whole set of theorems, algorithms and software developments, that will allow one to study a computational problem on all (or any) of the desired levels of numerical rigor. Key developments include fast and certified spectral methods and polynomial arithmetic, with subsequent formal verifications. There will be a strong feedback between the development of our tools and the applications that motivate it.
The project led by École Normale Supérieure de Lyon (LIP) has started in February 2021 and lasts for 4 years. Partners: Inria (teams Aric, Galinette, Lfant, Marelle, Toccata), École Polytechnique (LIX), Sorbonne Université (LIP6), Université Sorbonne Paris Nord (LIPN), CNRS (LAAS).
10.2.2 ANR GOSPEL
Participants: Jean-Christophe Filliâtre [contact], Andrei Paskevich, Armaël Guéneau.
A specification language extends a programming language by allowing code and specifications to be written in a single document. Examples include SparkAda, JML, and ACSL, which extend Ada, Java, and C with syntax for specifications.
By offering a specification language to programmers, one encourages them to document, test, and verify their code as they write it, not as a separate step that is too easily postponed. From a technical point of view, the presence of specifications makes it possible to test or verify each module independently and is the key to scalability. From a pragmatic point of view, embedding specifications in the code allows them to be automatically distributed (via a package management system) to every programmer; this is the key to practical adoption.
The GOSPEL project proposes to develop Gospel, a specification language that extends the programming language OCaml; to develop an ecosystem of tools based on Gospel; and to demonstrate and validate these tools via several case studies.
The project led by Inria Paris has started in October 2022 and lasts for 4 years. Partners: Inria Paris (team Cambium), Université Paris-Saclay (LMF), Tarides, Nomadic Labs.
10.2.3 Project “SecurEval” of PEPR Cybersécurité
Participants: Sylvain Conchon [contact].
The SecureVal project aims to design new tools, benefiting from new digital technologies, to verify the absence of hardware and software vulnerabilities, and carry out the proof of compliance required.
In order to deal effectively with modern digital systems, code analysis techniques, which originated in the world of critical systems, must be overhauled to adapt to the objectives of security assessments and to scale up to complex systems, combining dedicated functionalities and third-party libraries. For example, the design of new fault models, the support of emerging languages, the visualization of formal guarantees, the use of learning techniques to automate repetitive actions or optimize the extraction of relevant information, or the development of approaches combining static and dynamic analyses.
The project is led by CEA-List, it started in 2022 and lasts for 6 years.
10.2.4 Project I-Demo “Décysif”
The grant covers 3 PhD positions and 24 months of engineer position.
The Décysif project is a very new project started in december 2023, for 4 years. Its general goal is the promotion of formal verification for critical systems regarding cybersecurity. This project will fund our future research on Rust program verification, and it contains a workpackage dedicated towards industrialization of the Creusot tool.
The project is led by TrustInSoft company, with AdaCore and OCamlPro as other partners.
10.2.5 Inria Project LiberAbaci
Participants: Sylvie Boldo [contact].
The Défi Inria LiberAbaci is a collaborative project aimed at improving the accessibility of the Coq interactive proof system for an audience of mathematics students in the early academic years.
The head is Yves Bertot and the involved teams are: Cambium (Paris), Camus (Strasbourg), Gallinette (Nantes) PiCube (Paris), Spades (Grenoble), Stamp (Sophia Antipolis), Toccata (Saclay), LIPN (Villetaneuse).
11 Dissemination
Participants: Andrei Paskevich, Antoine Lanco, Armaël Guéneau, Claude Marché, Guillaume Melquiond, Jean-Christophe Filliâtre, Josué Moreau, Sylvain Conchon, Sylvie Boldo.
11.1 Promoting scientific activities
11.1.1 Scientific events: organisation
Member of the conference program committees
- S. Boldo, 30th IEEE Symposium on Computer Arithmetic, ARITH'2023
- S. Boldo, 15th NASA Formal Methods Symposium, NFM'2023
- S. Boldo, 14th International Conference on Interactive Theorem Proving, ITP'2023
- S. Conchon, 27th International Conference on Engineering of Complex Computer Systems, ICECSS 2023
- S. Conchon, Formal Methods in Computer Aided Design, FMCAD 2023
- G. Melquiond, 30th IEEE Symposium on Computer Arithmetic, ARITH'2023
- S. Boldo, 31st IEEE Symposium on Computer Arithmetic, ARITH'2024
- S. Boldo, 1st workshop on Programming for the Planet, PROPL'2024
- S. Boldo, 35th Journées Francophones des Langages Applicatifs, JFLA'24
11.1.2 Journal
Member of the editorial boards
- S. Boldo: member of the editorial board of IEEE Transactions on Emerging Topics in Computing (TETC), 2023.
- J.-C. Filliâtre: member of the editorial board of the Journal of Functional Programming, since 2011.
- J.-C. Filliâtre: member of the editorial board of the journal Formal Aspects of Computing, since 2021.
- G. Melquiond: member of the editorial board of Reliable Computing, since 2019.
- A. Paskevich, member of the editorial board of Formal Methods in System Design, since 2021.
11.1.3 Invited talks
- S. Boldo was invited speaker at the JFLA (Journées Francophones des Langages Applicatifs) in Praz-sur-Arly in February 2023.
- S. Boldo and A. Guéneau were invited speaker at the GT SCALP (a subgroup of the GDR IM) in Orléans in Novembre 2023.
- J.-C. Filliâtre, Why3, une plateforme pour la vérification déductive16, Journées FAC 2023, Toulouse, France
- J.-C. Filliâtre, 33Structures de données semi-persistantes, Collège de France, mars 2023
- G. Melquiond, “Numerical Computations and Formal Proofs”, Certified and Symbolic-Numeric Computation, May 22–26, 2023, web page
11.1.4 Leadership within the scientific community
- S. Boldo, elected chair of the ARITH working group of the GDR-IM (a CNRS subgroup of computer science) with L.-S. Didier (Univ. Toulon).
- S. Boldo, steering committee member of the IEEE International Symposium on Computer Arithmetic.
- J.-C. Filliâtre, chair of IFIP WG 1.9/2.15 verified Software.
11.1.5 Scientific expertise
- S. Conchon, member of a recruitment committee for a full assistant professor position in computer science at Sorbonne University, 2023.
- S. Conchon, member of a recruitment committee for a full professor position in computer science at Paris-Cité University, 2023.
11.1.6 Research administration
- S. Boldo, steering committee member of the IEEE International Symposium on Computer Arithmetic from 2019 to 2023.
- S. Boldo, president of the concours de l'agrégation d'informatique, 2022-2024.
- G. Melquiond, member of the Bureau du Comité des Projets of Inria-Saclay
11.2 Teaching - Supervision - Juries
11.2.1 Teaching
- S. Conchon and J.-C. Filliâtre, DIU Enseigner l'Informatique au Lycée, 2 weeks, rectorat de Versailles (together with T. Balabonski and K. Nguyen).
- J.-C. Filliâtre, Langages de programmation et compilation, 25h, L3, École Normale Supérieure, France.
- J.-C. Filliâtre, Les bases de l'algorithmique et de la programmation, 15h, L3, École Polytechnique, France.
- J.-C. Filliâtre, Compilation, 18h, M1, École Polytechnique, France.
- A. Guéneau, Programmation avancée, 12h, L3, ENS Paris-Saclay, France.
- A. Lanco, Introduction à l'informatique, 24h, L1, Université Paris-Saclay, France.
- A. Lanco, Programmation fonctionnelle, 24h, L2, Université Paris-Saclay, France.
- A. Lanco, Projet, 20h, L3, Université Paris-Saclay, France.
- A. Lanco, Sécurité des systèmes d'information, 24h, M1, Université Paris-Saclay, France.
- C. Marché, Proofs of Programs, 12h, M2, Master Parisien de Recherche en Informatique (MPRI).
- G. Melquiond, Initiation à la recherche, 12h, M1, MPRI, École Normale Supérieure Paris-Saclay, France.
- J. Moreau, Algorithmique, 16h, L3, Université Paris-Saclay, France.
- A. Paskevich, Vérification Déductive, 12h, M1, MPRI, Université Paris-Saclay, France.
- A. Paskevich, Programmation système, 56h, BUT2, IUT d'Orsay, Université Paris-Saclay, France.
11.2.2 Supervision
- PhD: A. Lanco, “Stratégies pour la réduction forte”, since Oct. 2019, supervised by T. Balabonski and G. Melquiond. Defended in December 2023 60.
- PhD: C. Pascutto, “Runtime and Deductive Verification of OCaml programs and applications to Mergeable Data Structures”, since June 2020, supervised by J.-C. Filliâtre. Defended in 2023 67.
- PhD: X. Denis, “Deductive program verification for Rust”, since Oct. 2020, supervised by J.-H. Jourdan and C. Marché. Defended in December 2023 51.
- PhD in progress: L. Andrès, “Formalization of a garbage collector for WebAssembly”, since Oct. 2021, supervised by J.-C. Filliâtre.
- PhD in progress: H. Mouhcine, “Preuves formelles en mathématiques appliquées: vérification d'un générateur de formules de quadrature”, since Oct 2021, supervised by S. Boldo, F. Clément, and M. Mayero.
- PhD in progress: J. Moreau, “A low-level programming language for formally verified computer algebra”, since Oct. 2022, supervised by G. Melquiond.
- PhD in progress: P. Geneau de Lamarlière, “Design of formally verified floating-point components”, since Sep. 2022, supervised by G. Melquiond.
- PhD in progress: P. Patault, “Conception et étude d'un langage de programmation adapté à la vérification déductive”, since Oct. 2023, supervised by J.-C. Filliâtre and A. Paskevich.
- PhD in progress: A. Golfouse, “Vérification de programme Rust avancée: invariants de types, code fantôme, possession fantôme et algèbre de ressources, concurrence et aliasing”, since Oct. 2023, supervised by J.-H. Jourdan and A. Guéneau.
11.2.3 Juries
- S. Boldo, reviewer of the habilitation of Guillaume Revy (U. Perpignan, 19 July 2023)
- S. Boldo, reviewer for a PhD at University of Melbourne, Australia in August 2023. Note this is an anonymous review.
- S. Boldo, member (maybe president) of the PhD defense of El-Mehdi El Arar (U. Paris-Saclay, 19 December 2023)
- S. Conchon, reviewer of the PhD defense of N. Nalpon, INSA Toulouse, March 13th 2023.
- S. Conchon, member and president of the PhD defense of D. Nizard, Université Paris-Saclay, April 12th 2023.
- S. Conchon, reviewer of the PhD defense of L. Sguerra, Mines Paris - PSL, April 19th 2023.
- S. Conchon, reviewer of the PhD defense of G. Raimondi, University of Rennes, December 18th 2023.
- C. Marché, reviewer of the PhD defense of W. Ouédraogo, Institut Polytechnique de Paris, Sep 15th, 2023.
- G. Melquiond, member of the jury of the PhD defense of Enzo Crance (U. Nantes, Dec 19th, 2023).
11.3 Popularization
11.3.1 Articles and contents
- S. Boldo, Le dilemme du fabricant de tables32, popularization journal La Recherche
11.3.2 Interventions
- S. Boldo, animation of a stand at “Fête de la science” each year.
12 Scientific production
12.1 Major publications
- 1 articleThe CoLiS Platform for the Analysis of Maintainer Scripts in Debian Software Packages.International Journal on Software Tools for Technology Transfer2022HALback to text
- 2 articleAutomated Formal Analysis of Temporal Properties of Ladder Programs.International Journal on Software Tools for Technology Transfer2462022, 977-997HALDOIback to text
- 3 articleA Coq Formalization of Lebesgue Integration of Nonnegative Functions.Journal of Automated Reasoning662022, 175–213HALDOIback to text
- 4 bookComputer Arithmetic and Formal Proofs: Verifying Floating-point Algorithms with the Coq System.ISTE Press - ElsevierDecember 2017, URL: https://hal.inria.fr/hal-01632617back to text
- 5 inproceedingsDeductive Verification with Ghost Monitors.POPL 2020 - 47th ACM SIGPLAN Symposium on Principles of Programming LanguagesNew Orleans, United States2020HALDOIback to text
- 6 articleDeclarative Parameterized Verification of Distributed Protocols via the Cubicle Model Checker.Fundamenta Informaticae1784February 2021, 347-378HALDOIback to text
- 7 inproceedingsA Three-tier Strategy for Reasoning about Floating-Point Numbers in SMT.Computer Aided Verification2017, URL: https://hal.inria.fr/hal-01522770back to text
- 8 inproceedingsAbstraction and Genericity in Why3.ISoLA 2021 - 9th International Symposium On Leveraging Applications of Formal Methods, Verification and Validation12476Rhodes, Greece2020HALDOIback to text
- 9 articleFormally Verified Approximations of Definite Integrals.Journal of Automated Reasoning622February 2019, 281-300HALDOIback to text
- 10 inproceedingsRustHornBelt: a semantic foundation for functional verification of Rust programs with unsafe code.PLDI 2022 - 43rd ACM SIGPLAN International Conference on Programming Language Design and ImplementationSan Diego CA USA, United StatesACMJune 2022, 841-856HALDOIback to text
12.2 Publications of the year
International journals
Invited conferences
International peer-reviewed conferences
National peer-reviewed Conferences
Scientific book chapters
Reports & preprints
12.3 Other
Scientific popularization
Educational activities
12.4 Cited publications
- 34 miscNVIDIA: Adoption of SPARK Ushers in a New Era in Security-Critical Software Developmen.2023back to text
- 35 inproceedingsMulti-Prover Verification of Floating-Point Programs.Fifth International Joint Conference on Automated Reasoning6173Lecture Notes in Artificial IntelligenceEdinburgh, ScotlandSpringerJuly 2010, 127--141URL: http://hal.inria.fr/inria-00534333back to text
- 36 bookNumérique et Sciences Informatiques, 24 leçons avec exercices corrigés. Terminale.Ellipses2020, URL: https://hal.inria.fr/hal-03023099back to text
- 37 bookNumérique et Sciences Informatiques, 30 leçons avec exercices corrigés. Première..Ellipses2019, URL: https://inria.hal.science/hal-02379073back to text
- 38 bookInformatique - MP2I/MPI - CPGE 1re et 2e années - Cours et exercices corrigés.Ellipses2022, URL: https://hal.inria.fr/hal-03886751back to text
- 39 inproceedingscvc5: A Versatile and Industrial-Strength SMT Solver.Tools and Algorithms for the Construction and Analysis of Systems13243Lecture Notes in Computer ScienceSpringer2022, 415--442back to text
- 40 manualACSL: ANSI/ISO C Specification Language, version 1.4.2009back to text
- 41 inproceedingsMETEOR : A successful application of B in a large project.Proceedings of FM'99: World Congress on Formal MethodsLecture Notes in Computer Science (Springer-Verlag)Springer VerlagSeptember 1999, 369--387back to text
- 42 articleLet's Verify This with Why3.International Journal on Software Tools for Technology Transfer (STTT)1762015, 709--727HALback to text
- 43 articleA Coq Formalization of Lebesgue Integration of Nonnegative Functions.Journal of Automated Reasoning662022, 175--213URL: https://hal.inria.fr/hal-03471095back to text
- 44 inproceedingsFormal Proof of a Wave Equation Resolution Scheme: the Method Error.Interactive Theorem Proving6172Lecture Notes in Computer ScienceSpringer2010, 147--162URL: http://hal.inria.fr/inria-00450789/enback to text
- 45 articleWave Equation Numerical Resolution: a Comprehensive Mechanized Proof of a C Program.Journal of Automated Reasoning504April 2013, 423--456URL: http://hal.inria.fr/hal-00649240/en/back to text
- 46 inproceedingsCombining Coq and Gappa for Certifying Floating-Point Programs.16th Symposium on the Integration of Symbolic Computation and Mechanised Reasoning5625Lecture Notes in Artificial IntelligenceGrand Bend, CanadaSpringerJuly 2009, 59--74back to text
- 47 articleFormal verification of numerical programs: from C annotated programs to mechanical proofs.Mathematics in Computer Science542011, 377--393URL: http://hal.inria.fr/hal-00777605back to textback to text
- 48 articleProofs of numerical programs when the compiler optimizes.Innovations in Systems and Software Engineering722011, 151--160URL: http://hal.inria.fr/hal-00777639back to text
- 49 articleAn overview of JML tools and applications.International Journal on Software Tools for Technology Transfer (STTT)73June 2005, 212--232back to text
- 50 inproceedingsAlt-Ergo 2.2.SMT Workshop: International Workshop on Satisfiability Modulo TheoriesOxford, United KingdomJuly 2018HALback to text
- 51 phdthesisDeductive Verification of Rust Programs.Université Paris-Saclay2023back to textback to text
- 52 techreportDeductive program verification for a language with a Rust-like typing discipline.Université de ParisSeptember 2020, URL: https://hal.science/hal-02962804back to text
- 53 inproceedingsCreusot: a Foundry for the Deductive Verication of Rust Programs.International Conference on Formal Engineering Methods - ICFEMLecture Notes in Computer ScienceMadrid, SpainSpringer2022, URL: https://hal.inria.fr/hal-03737878back to textback to text
- 54 articleCertifying the floating-point implementation of an elementary function using Gappa.IEEE Transactions on Computers6022011, 242--253URL: http://hal.inria.fr/inria-00533968/en/back to text
- 55 inproceedingsOptimizing Prestate Copies in Runtime Verification of Function Postconditions.22nd International Conference on Runtime Verification2022, URL: https://hal.inria.fr/hal-03690675v1back to textback to text
- 56 techreportAutomated Verification of Floating-Point Computations in Ada Programs.RR-9060InriaApril 2017, 53URL: https://hal.inria.fr/hal-01511183back to text
- 57 inproceedingsAutomating the Verification of Floating-Point Programs.Verified Software: Theories, Tools, and Experiments. Revised Selected Papers Presented at the 9th International Conference VSTTELecture Notes in Computer Science10712Heidelberg, GermanySpringerDecember 2017, URL: https://hal.inria.fr/hal-01534533/back to text
- 58 inbookOpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case.Computer Aided Verification: 27th International Conference, CAV 2015, San Francisco, CA, USA, July 18-24, 2015, Proceedings, Part ID.Daniel KroeningC. S.Corina S. PăsăreanuChamSpringer International Publishing2015, 273--289back to text
- 59 articleseL4: Formal verification of an OS kernel.Communications of the ACM536June 2010, 107--115back to text
- 60 phdthesisStratégies pour la réduction forte.Université Paris-Saclay2023back to textback to text
- 61 articleA formally verified compiler back-end.Journal of Automated Reasoning4342009, 363--446URL: http://hal.inria.fr/inria-00360768/en/back to text
- 62 inproceedingsThe Power of Log-Sum-Exp: Sequential Density Ratio Matrix Estimation for Speed-Accuracy Optimization.International Conference on Machine Learning139Proceedings of Machine Learning Research2021, 7792--7804URL: https://proceedings.mlr.press/v139/miyagawa21a.htmlback to text
- 63 inproceedingsZ3, An Efficient SMT Solver.TACAS4963Lecture Notes in Computer ScienceSpringer2008, 337--340back to text
- 64 bookHandbook of Floating-point Arithmetic (2nd edition).Birkhäuser BaselJuly 2018HALback to text
- 65 inproceedingsHardware-Dependent Proofs of Numerical Programs.Certified Programs and ProofsLecture Notes in Computer ScienceSpringerDecember 2011, 314--329URL: http://hal.inria.fr/hal-00772508back to text
- 66 inproceedingsLeveraging Formal Specifications to Generate Fuzzing Suites.OCaml Users and Developers Workshop, co-located with the 26th ACM SIGPLAN International Conference on Functional Programming2021, URL: https://hal.inria.fr/hal-03328646back to text
- 67 phdthesisRuntime Verification of OCaml Programs.Université Paris-Saclay2023back to textback to textback to text
- 68 articleA Why3 proof of GMP algorithms.Journal of Formalized Reasoning2019, URL: https://inria.hal.science/hal-02477578back to text
- 69 inproceedingsProving full-system security properties under multiple attacker models on capability machines.CSF 2022 - 35th IEEE Computer Security Foundations Symposium2022, URL: https://hal.inria.fr/hal-03826851back to text

