Section: New Results
Inverse modeling
Many of this year's studies have focused on inverse modeling, including the reconstruction of the Fukushima radionuclide source term. All were targeted to a particular application. However most of them include new methodological developments.
Estimation of errors in the inverse modeling of accidental release of atmospheric pollutant: Application to the reconstruction of the Fukushima Daiichi source term
Participants : Victor Winiarek, Marc Bocquet, Olivier Saunier [IRSN] , Anne Mathieu [IRSN] .
The aim of this research activity is the implementation of data assimilation methods, particularly inverse modeling methods, in the context of an accidental radiological release from a nuclear power plant and their application in the specific case of the Fukushima Daiichi accident. The particular methodological focus is the a posteriori estimation of the prior errors statistics. In the case of the Fukushima Daiichi accident, the number of available observations is small compared to the number of source parameters to retrieve and the reconstructed source is highly sensitive to the prior errors. That is the why they need to be well established and justified.
In this aim, three methods have been proposed: one method relies on an L-curve estimation technique, another one on the Desroziers' iterative scheme and the last method, assumed to be the most robust, relies on the maximum likelihood principle (generalized to a non-Gaussian context).
These three methods have been applied to the reconstruction of cesium-137 and iodine-131 source terms from the Fukushima Daiichi accident. Because of the poor observability of the Fukushima Daiichi emissions, these methods provide lower-bounds for cesium-137 and iodine-131 reconstructed activities. Nevertheless, with the new method based on semi-Gaussian statistics for the background errors, these lower-bound estimates, Bq for cesium-137, with an estimated standard deviation range of , and Bq for iodine-131, with an estimated standard deviation range of , are of the same order of magnitude as those provided by the Japanese Nuclear and Industrial Safety Agency, and about 5 to 10 times less than the Chernobyl atmospheric releases.
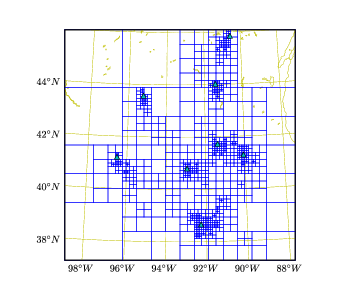
Optimal Representation of Source-Sink Fluxes for Mesoscale Carbon Dioxide Inversion
Participants : Lin Wu, Marc Bocquet, Frédéric Chevallier [LSCE, CEA] , Thomas Lauvaux [Department of Meteorology, Pennsylvania State University, USA] , Peter Rayner [School of Earth Sciences, University of Melbourne, Australia] , Ken Davis [Department of Meteorology, Pennsylvania State University, USA] .
This study is an application of our previous theoretical developments on a consistent Bayesian multiscale formalism to optimally design control space (in which control variables are to be estimated). We construct the optimal adaptive representations of the surface fluxes for mesoscale carbon dioxide inversions. Such representations are taken from a large dictionary of adaptive multiscale grids. These optimal representations are obtained by maximizing the number of Degrees of Freedom for the Signal (DFS) that measures the information gain from observations to resolve the unknown fluxes. Consequently information from observations can be better propagated within the domain through these optimal representations.
The optimal representations are constructed using synthetic continuous hourly carbon dioxide concentration data in the context of the Ring 2 experiment in support of the North American Carbon Program Mid Continent Intensive (MCI). Compared with the regular grid at finest scale, optimal representations can have similar inversion performance with far fewer grid cells. For the Ring 2 network of eight towers, in most cases, the DFS value is relatively small compared to the number of observations (DFS/). In this multiscale setting, scale-dependent errors due to the aggregation of flux variables are identified and explicitly formulated for more reliable inversions. It is recommended that this aggregation error should be taken into account, especially when the correlations in the errors of a priori fluxes are physically unrealistic. The optimal multiscale grids allow to adaptively mitigate the aggregation error.
|