Section: New Results
A posteriori error analysis of sensitivities
Participants : Roland Becker, Daniela Capatina, Robert Luce, David Trujillo.
Most practical applications involve parameters of different origins: physical (viscosity, heat conduction), modeling (computational domain, boundary conditions) and numerical (mesh, stabilization parameters, stopping criteria, values of a turbulence model). Numerical simulations can provide information related to the (first order) sensitivity of a quantity of physical interest with respect to different parameters: . Their computation can help to validate the physical model, to explain unexpected behaviour and also to guide efforts to improve both the physical and the computational models.
A posteriori error estimates for the functional itself, for fixed values of the parameters , are well-known, cf. for example [47] where a goal-oriented error control is achieved by introducing an adjoint problem. Our goal is to provide a general framework for the a posteriori error estimation of sensitivities , which has not been given yet in the literature.
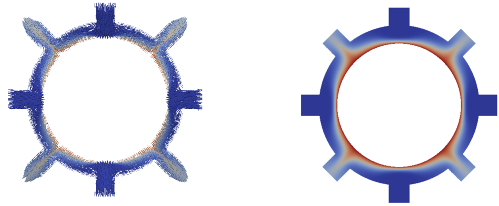
So far, we have applied the proposed method to the computation of the Nusselt number measuring the efficiency of a cooling process, described in the project Optimal. A cold liquid is injected in a annular domain through several inlets in order to cool a heated interior stator.
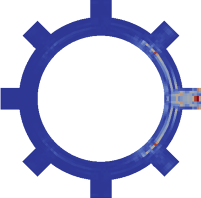
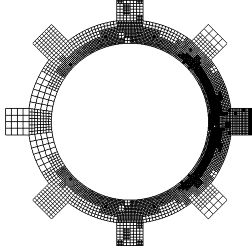
First numerical results, including adaptation with respect to the functional and to the sensitivity, have been carried out with the library Concha. They have been presented in [33] , [30] . In Figure 10 one may see the computed temperature and velocity field, while the a posteriori error estimator for the sensitivity of the Nusselt number with respect to the inflow speed at the right-hand side inlet, as well as the adapted mesh, are given in Figure 11 .
In the future, several important aspects related to the adaptive method are still to be investigated such as design of an appropriate adaptive algorithm, proof of its convergence and optimality etc.