Section: New Results
Viscoelastic fluids modeling and numerical simulation
Participants : Roland Becker, Daniela Capatina, Didier Graebling, Julie Joie.
We have continued our activities with respect to numerical simulations of polymer flows.
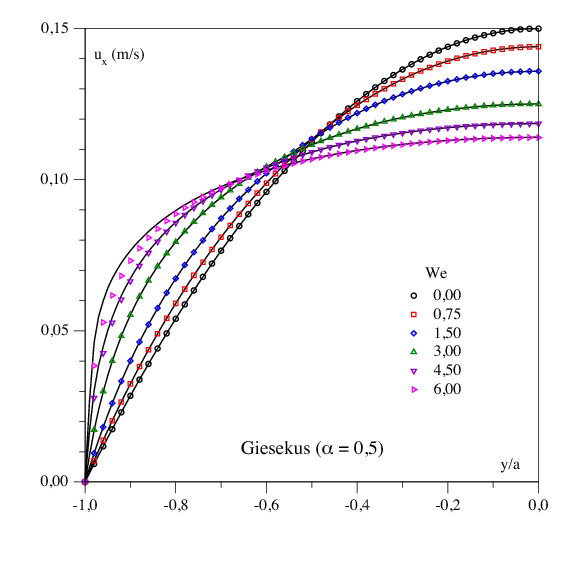
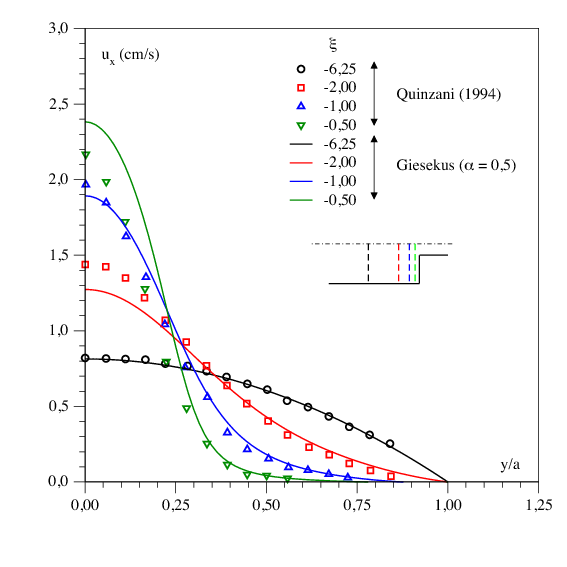
We have further validated [32] the code on both triangular and quadrilateral 2D meshes, by using a mixed non-conforming/DG method. In the case of Giesekus model, comparisons of velocity profile with semi-analytical solutions for Poiseuille flow [70] and with experimental data [73] for the 4:1 contraction are respectively shown in Figures 12 and 13 ).
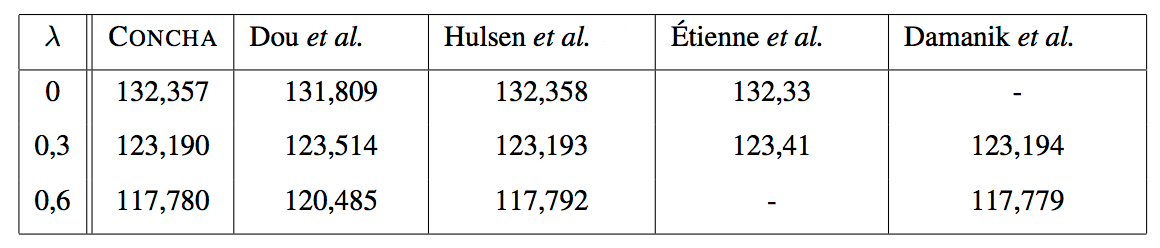
The quadrilateral scheme needs an additional stabilization term, in order to ensure uniform consistency and stability for the underlying linear problem. It has been tested in particular on the benchmark case of flow around a 2D cylinder, for which our code converged for high values of the Weissenberg number (We > 70). We have computed the drag and compared it, see Figure 14 , with numerical data found in the literature [58] , [65] , [76] , [57] in the case of the Oldroyd-B model.
The system associated to this quasi-linear model has been solved on rather fine meshes (of about 10 elements) thanks to a multigrid solver based on a Vanka type preconditionner. We have worked on the extension of the multigrid method to more complex and more realistic polymer models, involving nonlinear terms in the constitutive law such that Phan Thien-Tanner and Giesekus models.
The unsteady case has also been treated for different geometries.
The parallelization of the library is ongoing work as described in the section 5.3 ; first tests have been carried on in the case of viscoelastic liquids.
In order to better describe real polymer flows, the thermal aspects have to be taken into account. As a first step, the coupling of the flow with the energy equation in the Newtonian case was considered in [38] , by using a conservative variable. Our next objective is to simulate anisothermal viscoelastic flows, including typical effects such that thermo-dependent viscosity and viscous heating.
With these tools, the long-term goal is to successively build up robust and efficient software in order to tackle design problems.
Moreover, we intend to consider other models of non-Newtonian fluids employed in other application domains such as biomedecine.