Section: Scientific Foundations
Dynamics of complex systems
GEOSTAT is studying complex signals under the point of view of nonlinear methods, in the sense of nonlinear physics i.e. the methodologies developed to study complex systems. Linear methods in signal processing refer to the standard point of view under which operators are expressed by simple convolutions with impulse responses. Linear methods in signal processing are widely used, from least-square deconvolution methods in adaptive optics to source-filter models in speech processing. Fundamentally, linear signal processing is deeply rooted in stationarity hypothesis of the underlying processes, an hypothesis that is questioned in complex systems whose signals are the acquisitions. Linear methods do not unlock the multiscale structures and cascading variables of primarily importance as previewed by the physics of the phenomena. This is the reason why new approaches, such as DFA (Detrented Fluctuation Analysis), Time-frequency analysis etc. have appeared during the last decades. Understanding the dynamics of complex systems is recognized as a new discipline, which makes use of theoretical and methodological foundations coming from nonlinear physics, the study of dynamical systems and many aspects of computer science. One of the challenges is related to the question of emergence in complex systems: large-scale effects measurable macroscopically from a system made of huge numbers of interactive agents [33] , [30] , [45] , [37] . Some quantities related to nonlinearity, such as Lyapunov exponents, Kolmogorov-Sinai entropy can be computed at least in phase space [31] . Consequently, knowledge from acquisitions of complex systems (which include complex signals could be obtained from information about the phase space. A result from F. Takens [41] about strange attractors in turbulence has motivated the determination of discrete dynamical systems associated to time series [35] , and consequently the theoretical determination of nonlinear characteristics associated to complex acquisitions. Emergence phenomena can also be traced inside complex signals themselves, by trying to localize information content geometrically. Fundamentally, in the nonlinear analysis of complex signals there are broadly two approaches: characterization by attractors (embedding and bifurcation) and time-frequency, multiscale/multiresolution approaches. Time-frequency analysis [32] and multiscale/multiresolution are the subjects of intense research and are profoundly reshaping the analysis of complex signals by nonlinear approaches [29] , [34] . In real situations, the phase space associated to the acquisition of a complex phenomenon is unknown. It is however possible to relate, inside the signal's domain, local predictability to local reconstruction and deduce from that Local Predictability Exponents [5] [20] . The LPEs are defined at any point in the signal's domain, they relate, but are different to other kinds of exponents used in the nonlinear analysis of complex signals. We are working on their relation with:
-
properties in universality classses,
-
the geometric localization of multiscale properties in complex signals,
-
cascading characteristics of physical variables,
-
optimal wavelets...
The alternative approach taken in GEOSTAT is microscopical, or geometrical: the multiscale structures which have their "fingerprint" in complex signals are being isolated in a single realization of the complex system, i.e. using the data of the signal itself, as opposed to the consideration of grand ensembles or a wide set of realizations. This is much harder than the ergodic approaches, but it is possible because a reconstruction formula such as the one derived in [42] is local and reconstruction in the signal's domain is related to predictability.
Nonlinear signal processing is making use of quantities related to predictability. For instance the first Lyapunov exponent
with
(
(
(
(
(
with
|
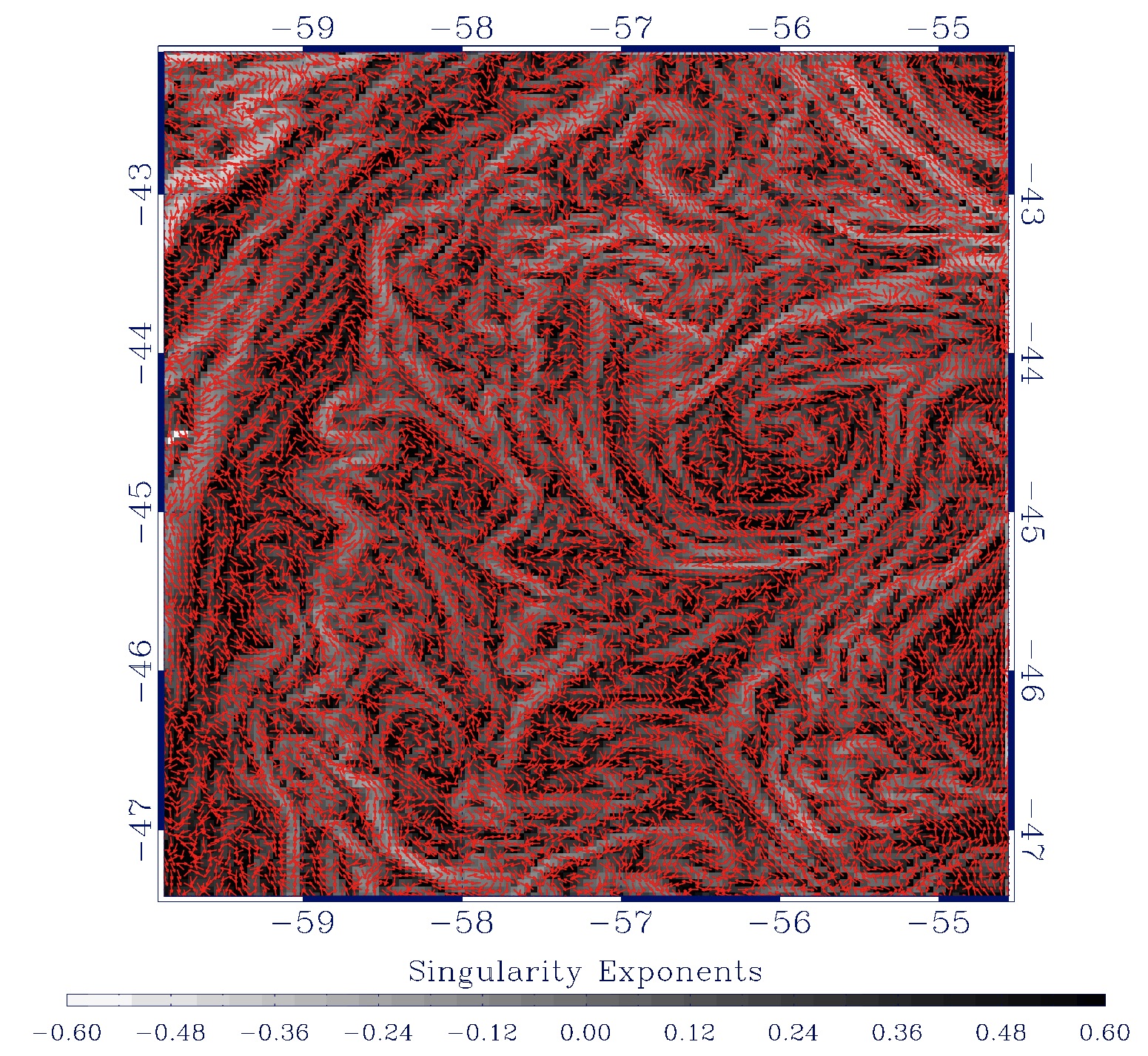
To take an example, we give some insight about the collaboration with LEGOS Dynbio team about high-resolution ocean dynamics from microcanonical formulations in nonlinear complex signal analysis. LPEs relate to the geometric structures linked with the cascading properties of indefinitely divisible variables in turbulent flows. Cascading properties can be represented by optimal wavelets (OWs); this opens new and fascinating directions of research for the determination of ocean motion field at high spatial resolution. OWs in a microcanonical sense pave the way for the determination of the energy injection mechanisms between the scales. From this results a new method for the complete evaluation of oceanic motion field is introduced; it consists in propagating along the scales the norm and the orientation of ocean dynamics deduced at low spatial resolution (geostrophic from altimetry and a part of ageostrophic from wind stress products). Using this approach, there is no need to use several temporal occurrences as in Optical Flow, Maximum Cross Correlation or FSLE techniques. Instead, the proper determination of the turbulent cascading and energy injection mechanisms in oceanographic signals allows the determination of oceanic motion field at the SST or Ocean colour spatial resolution (pixel size: 4 kms) which often go beyond the results obtained with other models (e.g. SQG models). We use the Regional Ocean Modelling System (ROMS) to validate the results on simulated data and compare the motion fields obtained with other techniques. See figure 1 .