Section: Scientific Foundations

Multiscale modeling and computations

Spatial complexity: collective motion of cells

The collective motion of cells (bacteries on a gel or endothelial cells during angiogenesis) is a fascinating subject, that involves a combinaison of random walk and chemotaxis. The modeling of these problems is still active, since the pioneering works of Keller and Segel, and the mathematical study of the arising equations is a very active area of research.

Vincent Calvez focuses its effort on the following questions:

• Mathematical analysis of the Keller-Segel model

  [In collaboration with J.A. Carrillo and J. Rosado (UAB, Barcelona)]

  Following McCann 1997 and Otto 2001, we interpret the classical Keller-Segel system for chemotaxis as a gradient flow in the Wasserstein space. The free-energy functional turns out to be homogeneous. This viewpoint helps to understand better blow-up mechanisms, and to derive rates of convergence towards self-similar profiles. We investigate more precisely linear diffusion, porous medium diffusion and fast diffusion in competition with various interaction kernels.

  [In collaboration with N. Meunier (Paris 5) and R. Voituriez (Paris 6)]

  Another project consists in analyzing some variant of the Keller-Segel system when the chemoattractant is secreted at the boundary of the domain. This is motivated by modeling issues in cell polarization.

• Kinetic models for bacterial collective motion

  Figure 1. Bacterial waves traveling in a narrow channel (experiments) (Figure from the PhD thesis of J. Saragosti, Institut Curie 2010).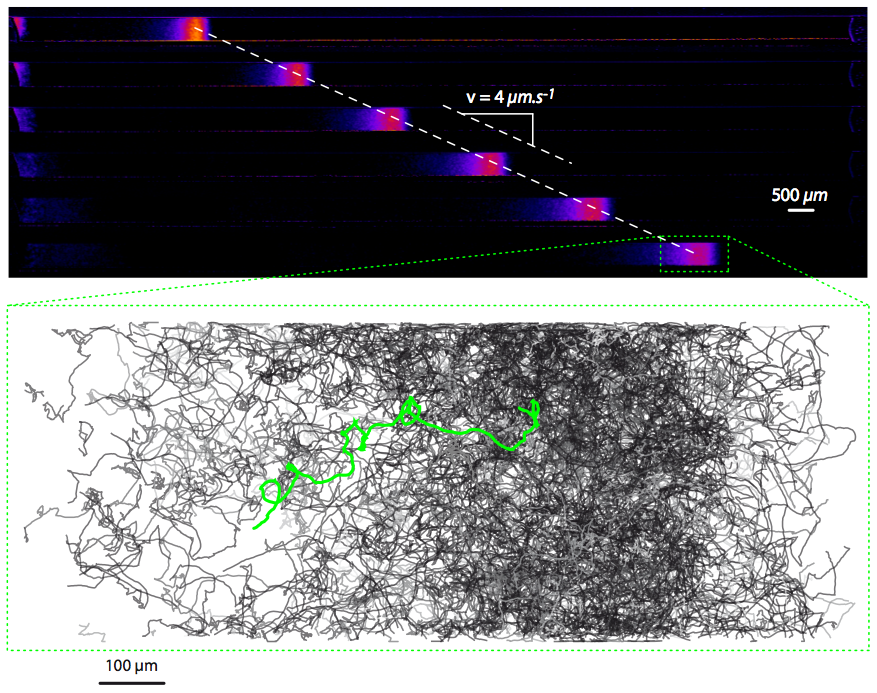

  Figure 2. (left) Numerical simulation of a traveling pulse obtained with the kinetic model (right) Comparison between the bacteria density measured experimentally (blue dots) and the density computed from the kinetic model.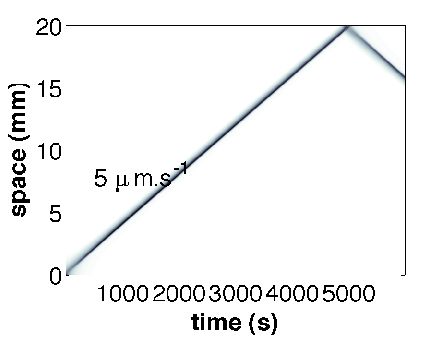

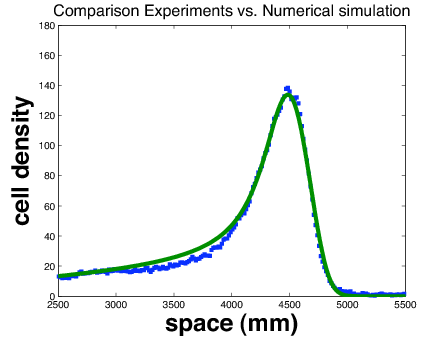
  We have investigated kinetic models for bacterial chemotaxis following Alt and co-authors, Erban and Othmer, Dolak and Schmeiser.

  We have developped a quantitative approach based on a couple of experiments performed by J. Saragosti in the team of A. Buguin and P. Silberzan (Institut Curie, Paris). These experiments describe with full statistical details solitary waves of bacteria E. coli in narrow channels. On the first set of experiments we have demonstrated that the drift-diffusion approximation of the kinetic model is valid and it fits the data very well (publication in PLoS Comput. Biol. 2010). On the second set of experiments (Fig. 1 ) we have simulated the kinetic model to obtain the best results as compared to the data (Fig. 2 ) (publication in PNAS 2011). Interestingly enough, the collaboration has led to the first experimental evidence of directional persistence of E. coli (the deviation angle after tumbling is smaller when the trajectory before tumbling goes in a favorable direction). We have demonstrated that this "microscopic effect" has a significant macroscopic influence on the solitary wave ($+30\%$ for the speed of the wave).

  Based on these encouraging results, we have started a synthetic analysis of hyperbolic equations for chemotaxis and traveling waves.

  In collaboration with Ch. Schmeiser (Univ. Vienna) we have investigated a simple (linear) kinetic equation for bacterial chemotaxis. We have obtained the existence of a stationary cluster (stable density distribution). We aim at applying the hypocoercivity results of Dolbeault-Mouhot-Schmeiser to derive a quantitative speed of relaxation towards the stable configuration. This work is under finalization.

  In collaboration with N. Bournaveas (Univ. Edinburgh), C. di Russo (Univ. Lyon 1) and M. Ribot (Univ. Nice Sophia-Antipolis) we are studying hyperbolic models for cell motion. We improve the results obtained by Natalini-di Russo. These models are preliminary models which are to be complexified in order to describe growth of biofilms. This work is under progress.

  In collaboration with E. Bouin and G. Nadin, we are analysing traveling waves arising in kinetic-growth equations. Namely, we study the coupling between a simple kinetic BGK operator (relaxation towards a given Maxwellian) and a logistic growth term. We have improved earlier results by Gallay-Raugel and Fedotov concerning the one-dimensional case with only two velocities. This work has been submitted. We continue the analysis with the full BGK operator. Counter-intuitive results have to be investigated further.

Modeling of spontaneous cell polarization

Figure 3. 2D numerical simulations of cell polarization on a round shaped cell. (Top) The actin network carries the attractive field: polarization occurs. (Bottom) The microtubules carry the attractive field: we observe no polarization. (Work in progress; simulations are done with FreeFEM++)

We have analysed recent models describing spontaneous polarization of cells (e.g. neuron growth cones or budding yeast). These models combine a diffusive term (in the cytoplasm) plus an advective field created at the membrane and diffusing in the cytoplasm (accounting for the actin network or the microtubules). This can be compared to the classical Keller-Segel model where diffusion competes with a non-local attractive field. Going beyond linear stability analysis we have used our know-how of the Keller-Segel system to derive global existence (no polarization) and blow-up (possibly polarization) criteria. We have also performed some numerical experiments to determine the models which exhibit spontaneous polarization. We have confirmed the prediction made by the physicists claiming that the microtubules cannot drive the cell into spontaneous polarization whereas the actin network can (Fig. 3 ).

Preliminaries results have been published in CRAS 2010 and SIAM J. Appl. Math (in press). We continue this project towards comparison with experimental data obtained in Matthieu Piel's lab at Institut Curie. A secondary goal consists in deriving a mechanistic model for the growth of the fission yeast Pombe. This is an ongoing work with A. Boudaoud (ENS de Lyon), N. Meunier (Univ. Paris 5), M. Piel (Institut Curie), P. Vigneaux (ENS de Lyon) and R. Voituriez (Univ. Paris 6). This is part of an ANR project JCJC, named "MODPOL" (Jan. 2012 – Dec. 2014). The project is coordinated by V. Calvez. It involves Th. Lepoutre (INRIA Dracula), N. Meunier (Univ. Paris 5), M. Piel (Institut Curie), P. Vigneaux (ENS de Lyon) and R. Voituriez (Univ. Paris 6).

Polymerization-fragmentation processes

Figure 4. Dynamics of trajectories of the control system projected on the simplex. (left) Remarkable sets in the simplex: the line of eigenvectors parametrized by the control parameter, and the small "ergodic" set. (middle) All trajectories eventually enter the ergodic set. (right) We prove a tunelling effect: all trajectories are confined in a neighbourhood of the ergodic set, and moves towards it.

In collaboration with M. Doumic (INRIA Bang) and P. Gabriel (INRIA Beagle) we have studied the behaviour of the eigenvalue problem for genuine growth-fragmentation equations. We have focused on the dependence of the couple eigenvalue-eigenvector with respect to the growth and fragmentation coefficients. We have mainly used blowing-techniques and asymptotic estimates. We have shown counter-intuitive (non-monotonic) dependence. We have also discussed the possible consequences on applications.

Together with P. Gabriel (INRIA Beagle) we are investigating the optimal control problem for a baby polymerization-fragmentation process mimicking the controlled growth of PrPres (prion) polymers. It consists in a three compartments system (small, intermediate and large polymers) with linear transitions between the compartments. We have a single control parameter acting on the fragmentation process.

We first assume that the control parameter has to be chosen constant. Under certain conditions, there is a best possible choice with infinite-time horizon. It maximizes the exponential growth by optimizing the eigenvalue of the polymerization-fragmentation matrix.

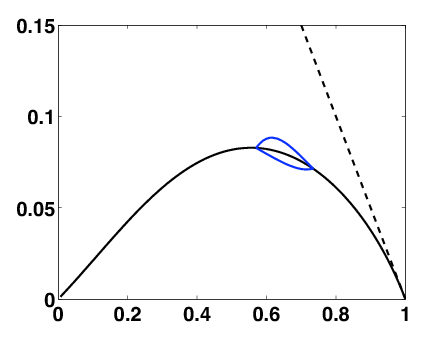
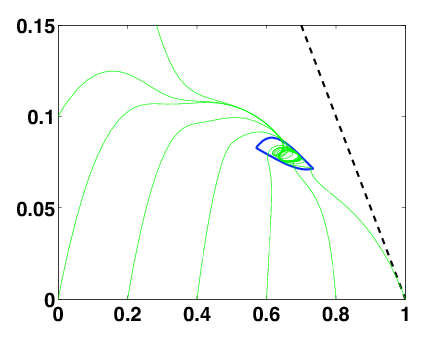
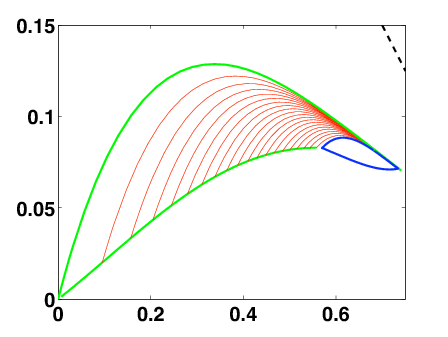
When we relax the condition of constant control, we have to deal with an optimal control problem. It can be translated into a Hamilton-Jacobi-Bellman equation. Although it is a very degenerated case, we can prove existence and uniqueness of an infinite-horizon eigenvalue, as in the constant case. We use the notion of ergodic set introduced by Arisawa-Lions (1998). The success of the proof relies on refined analysis of the dynamics of close-to-optimal trajectories projected on the simplex (Fig. 4 ). This work is under finalization.

Complex rheology

To investigate the growth of a tumor it is crucial to have a correct description of its mechanical aspects. Tumoral and normal cells may be seen as a complex fluid, with complex rheology.

Numerical investigations of complex flows is studied by P. Vigneaux who develops new numerical schemes fo Bingham type flows.