Section: New Results
Optimum design in fluid dynamics and its couplings
In computational sciences for physics and engineering, Computational Fluid Dynamics (CFD) are playing one of the major roles in the scientific community to foster innovative developments of numerical methodologies. Very naturally, our expertise in compressible CFD has led us to give our research on numerical strategies for optimum design a particular, but not exclusive focus on fluids.
Cooperation and competition in multidisciplinary optimization
Participants : Étienne Baratchart [ENSEIBB MATMÉCA] , Jean-Antoine Désidéri, Régis Duvigneau, Adrien Zerbinati.
The framework of our research aims to contribute to numerical strategies for PDE-constrained multiobjective optimization, with a particular emphasis on CPU-demanding computational applications in which the different criteria to be minimized (or reduced) originate from different physical disciplines that share the same set of design variables. These disciplines are often fluids, as a primary focus, coupled with some other discipline, such as structural mechanics.
Our approach to competitive optimization is based on a particular construction of Nash games, relying on a split of territory in the assignment of individual strategies. A methodology has been proposed for the treatment of two-discipline optimization problems in which one discipline, the primary discipline, is preponderant, or fragile. Then, it is recommended to identify, in a first step, the optimum of this discipline alone using the whole set of design variables. Then, an orthogonal basis is constructed based on the evaluation at convergence of the Hessian matrix of the primary criterion and constraint gradients. This basis is used to split the working design space into two supplementary subspaces to be assigned, in a second step, to two virtual players in competition in an adapted Nash game, devised to reduce a secondary criterion while causing the least degradation to the first. The formulation has been proved to potentially provide a set of Nash equilibrium solutions originating from the original single-discipline optimum point by smooth continuation, thus introducing competition gradually. This approach has been demonstrated over a testcase of aero-structural aircraft wing shape optimization, in which the eigen-split-based optimization reveals clearly superior [33] .
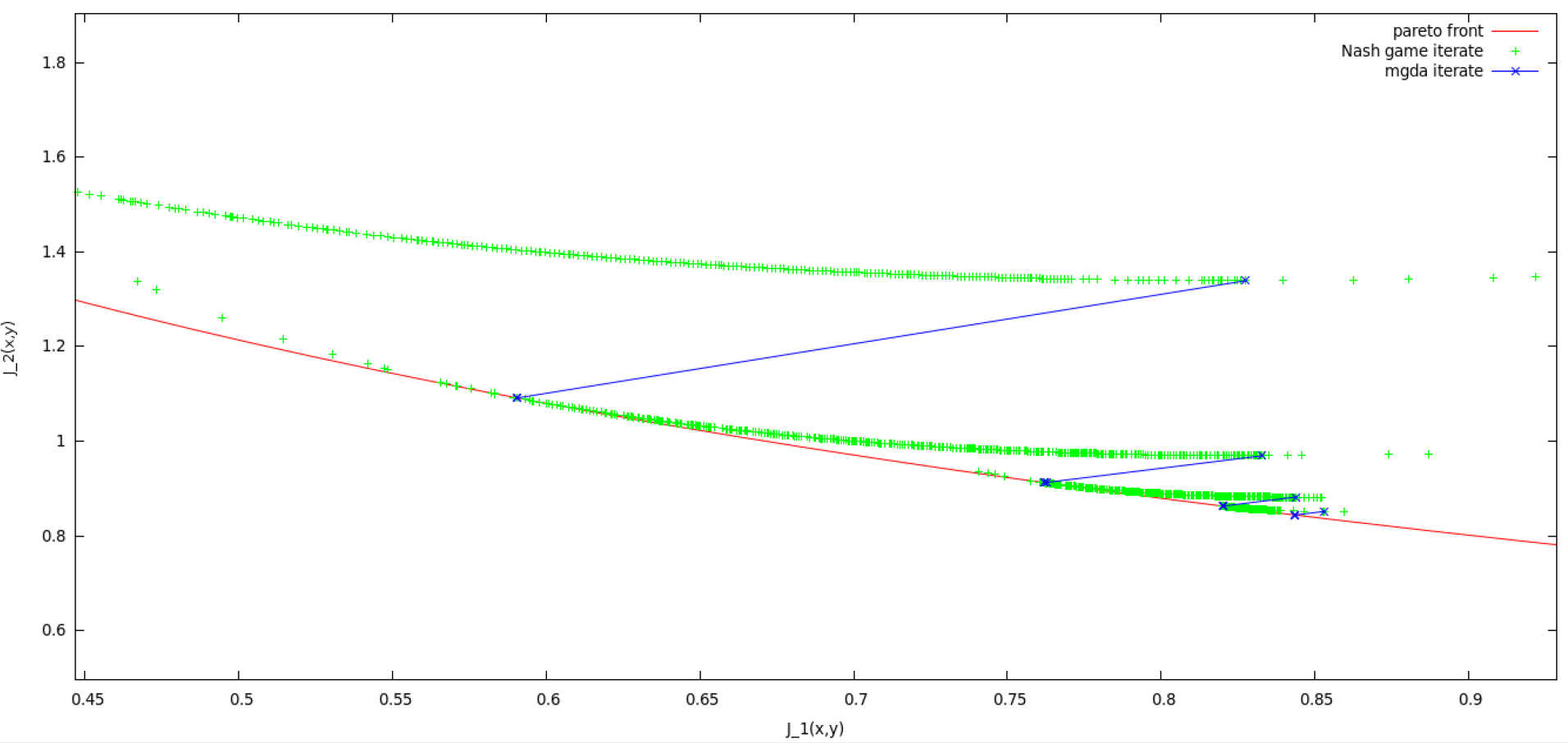
While the two-discipline method is currently being applied to various complex physical multiobjective situations (see in particular 6.2.2 , 6.2.6 , 6.2.7 , 6.2.8 ), the method has been extended to situations involving more than two objectives when the initial point is Pareto-optimal. Then, a particular convex combination of the criteria is locally stationary, and the two-discipline strategy can be applied using this combination as preponderant criterion, and a particular other criterion as secondary one. Whence, the proposed split of territory produces a continuum of Nash equilibrium points tangent to the Pareto set. This theoretical result has been illustrated in the context of a simpler numerical experiment by E. Baratchart during his internship [53] , see Fig. 3 .
|
Our approach to cooperative optimization is based on a result of convex analysis established for a general unconstrained multiobjective problem in which all the gradients are assumed to be known. The theorem [58] states that in the convex hull of the gradients, there exists a unique vector of minimal norm, ; if it is nonzero, the vector is a descent direction common to all criteria; otherwise, the current design point is Pareto-optimal. This result led us to generalize the classical steepest-descent algorithm by using the vector as search direction. We refer to the new algorithm as the multiple-gradient descent algorithm (MGDA). The MGDA yields to a point on the Pareto set, at which a competitive optimization phase can possibly be launched on the basis of the local eigenstructure of the different Hessian matrices. This general formulation fosters several connected studies detailed in 6.2.3 .
Virtual games for coupling global to local shape optimization
Participant : Régis Duvigneau.
In several engineering problems, the system to optimize is characterized by some parameters that define global shape properties, while remaining parameters define local shape modifications. Of course, these two sets of parameters do not play the same role and have not the same impact on the cost functional value. Therefore, we are studying how to construct an efficient optimization strategy that takes benefit of this global / local splitting of parameters.
A typical aerodynamic shape optimization problem has been studied, that consists of a lift-constrained drag minimization for a transonic wing, whose sections are defined by two B-Spline curves whereas global shape characteristics are defined by five parameters (span, roottip length ratio, angle of attack, twist angle, sweep angle). It has been found that the naive simultaneous optimization of all parameters failed, due to the multimodality of the problem. Alternatively, the use of a virtual game strategy, based on a splitting between the local and global parameters, yields a satisfactory result for a moderate cost [47] .
Multiple-Gradient Descent Algorithm (MGDA)
Participants : Jean-Antoine Désidéri, Régis Duvigneau, Adrien Zerbinati.
Basic experiments and validation
In multi-objective optimization, the knowledge of the Pareto set provides valuable information on the reachable optimal performance. A number of evolutionary strategies (PAES, NSGA-II, etc), have been proposed in the literature and proved to be successful to identify the Pareto set. However, these derivative-free algorithms are very demanding in terms of computational time. Today, in many areas of computational sciences, codes are developed that include the calculation of the gradient, cautiously validated and calibrated.
In [50] , MGDA has been tested over a number of classical multiobjective-optimization testcases, and found successful to converge to Pareto-optimal solutions in situations of either convex or concave Pareto sets. Additionally, MGDA and PAES [61] were found to have complementary merits, making a hybrid method promising.
Metamodel-supported CFD optimization by MGDA
Using MGDA in a multi objective optimization problem requires the evaluation of a large number of points with regard to criteria, and their gradients. In the particular case of a CFD problems, each point evaluation is very costly since it involves a flow computation, possibly the solution of an adjoint-equation. To alleviate this difficulty, we have proposed to construct metamodels of the functionals of interest (lift, drag, etc) and to calculate approximate gradients by local finite differences. These metamodels are updated throughout the convergence process to the evaluation of the new design points by the high-fidelity model, here the 3D compressible Euler equations.
This variant of MGDA has been tested successfully over a problem of external aerodynamic optimum-shape design of an aircraft wing consisting of reducing wave-drag, and augmenting lift. After only a few cycles of database updates, the Pareto front visibly forms, and this result is achieved at a very moderate computational cost. This variant is currently being tested and extended to an internal flow optimization problem related to an automobile air-conditioning system and governed by the Navier-Stokes equations. This more difficult problem has been proposed by Renault within the OMD2 ANR project.
MGDA in functional setting
One aspect of the theoretical result concerning the minimal-norm element is that, regardless the possibly-functional setting of the problem in case of a distributed system, the descent-direction is identified in the standard -dimensional vector space (: the number of objective functions).
This observation has led to examine the application of MGDA in the functional setting of domain-decomposition methods (DDM) in which a functional criterion and a functional control can be defined at each interface independently permitting to formulate the DDM problem as a multi-objective optimization. On-going research in this area is related to the necessary preconditioning, or normalization procedure, of the gradients.
Flow control
Participants : Régis Duvigneau, Jérémie Labroquère.
Shape optimization methods are not efficient to improve the performance of fluid systems, when the flow is characterized by a strong unsteadiness related to a massive flow separation. This is typically the case for the flow around an automotive body or a wing in stall condition. To overcome this difficulty, flow control strategies are developed, that aim at manipulating vortex dynamics by introducing some active actuators, such as periodic blowing/suction jets. In this context, the choice of the control parameters (location, amplitude, frequency) is critical and not straightforward. Therefore, a numerical study is conducted to i) improve the understanding of controlled flows ii) develop a methodology to determine optimal control parameters by coupling the controlled flow simulation with optimization algorithms. Two research axes have been considered :
-
the solution of the unsteady sensitivity equations derived from the state equations, to exhibit the dependency of the flow dynamics with respect to the control ;
-
the optimization of control parameters using a statistical metamodel-based strategy. First results show the efficiency of such an approach for laminar flow problems [31] , [44] .
Optimum shape design in aerodynamics by the adjoint method
Participants : Manuel Bompard, Sébastien Bourasseau, Jean-Antoine Désideri, Jacques Peter [Research Engineer, ONERA/DSNA] .
At ONERA, compressible flow simulations governed by the Euler or Navier Stokes (RANS) equations are conducted with the software elsA [57] that admits both structured and unstructured-grid formulations. Local aerodynamic optimizations are made with a version that includes the calculation of the shape gradient via the solution of an adjoint equation. The discrete adjoint is calculated formally step-by-step to include the various derivative terms involved, and is being enhanced gradually to account for more complex models. In particular, for RANS computations, this gradient today includes the differentiation of the turbulence model.
Metamodels including derivative informatio.
In this context, to alleviate the cost of an optimum-shape design in aerodynamics, M. Bompard in his thesis [26] , has examined how metamodels, firstly based on functional values only, could be used to determine shortcuts in the convergence process. Second, when the gradient w.r.t. the design parameters is known, the gradients of functionals of interest, that is, most commonly, aerodynamic coefficients, are calculated. Thus, these derivative informations can also used to construct more elaborate metamodels. Such constructions have also been studied systematically and used efficiently in global optimizations [37] ; in particular co-Kriging and Support-Vector Regression, for which a technique to adjust automatically the free parameters has been proposed based on a simplification of the leave-one-out test.
Parameterization-free local optimization
When the derivatives of the functionals w.r.t. the volume geometry, , have been calculated, it is also possible to calculate the gradient w.r.t. surface coordinates, . Since the surface deformation steers the entire mesh movement, often through analytical dependencies, M. Bompard [26] has also examined how could be used directly in a local aerodynamic optimization. However, it is well-known that the distribution of is very irregular, and its usage in the optimization loop necessitates that adequate smoothing procedures be elaborated. Partial success was achieved in this area, still subject to research.
Aero-structural optimization
Participants : Gérald Carrier [Research Engineer, ONERA/DAAP] , Jean-Antoine Désideri, Imane Ghazlane.
In industry, aircraft wings are designed by accounting for several multidisciplinary couplings. Certainly of greatest importance is the coupling, or concurrency, between aerodynamic optimization and structural design. At ONERA, in the former thesis of M. Marcelet, the aerodynamic gradient has been extended to account for (the main terms of) static fluid-structure interaction, commonly referred to as the “aeroelastic gradient”.
In her thesis, I. Ghazlane has extended M. Marcelet's work to take into account, in the aeroelastic gradient, the terms originating from the differentiation of the wing-structural model. In this development, the wing structure is treated as an equivalent Euler-Bernoulli beam. These formal extensions have been validated by an extensive experimentation. Additionally, special post-processing procedures are applied to evaluate accurately the various physical contributions to drag. As a result, the numerical tools necessary to conduct a very realistic aircraft wing optimization are now set up and are being exploited [38] . It is also envisaged to conduct a two-objective optimization (drag and mass reduction) via a Nash game using our optimization platform FAMOSA.
Sonic boom reduction
Participants : Gérald Carrier [Research Engineer, ONERA/DAAP] , Jean-Antoine Désideri, Andrea Minelli, Itham Salah El Din [Research Engineer, ONERA/DAAP] .
When an aircraft flies at supersonic speed, it generates at ground level an N-shaped shock structure which can cause serious environmental damage (“sonic boom”). Thus a problem of interest in aerodynamic optimization is to design such an aircraft to reduce the intensity of the sonic boom while maintaining the aerodynamic performance (drag minimization under lift constraint). Andrea Minelli's aimed at contributing to this two-discipline optimization problem. In the first part of his work, an inverse problem has been formulated and solved for “shaped sonic boom” and found in excellent agreement with the George-Seebass-Darden theory [60] for the calculation of the Whitham function corresponding to the lowest-boom (axisymmetric) shape. The method is currently being extended to account for more general geometries. Besides, aero-acoustic optimizations have been realized successfully by coupling the aerodynamic optimizer (based on Euler calculations by the elsA sofware) with the sonic-boom computation in a Nash game formulation. These experiments, conducted with our optimization platform FAMOSA, have demonstrated that starting from the shape optimized aerodynamically, one could retrieve smoothly a shape corresponding to nearly-optimal sonic-boom reduction.
Helicopter rotor blade optimization in both situations of hovering and forward flight
Participants : Michel Costes [Research Engineer, ONERA/DAAP] , Jean-Antoine Désideri, Arnaud Le Pape [Research Engineer, ONERA/DAAP] , Enric Roca Leon.
E. Roca Leon has recently started at ONERA a CIFRE thesis supported by EUROCOPTER, Marignane. This thesis follows the doctoral thesis of A. Dumont in which the adjoint-equation approach was used to optimize a rotor blade in hovering flight. The goal of this new thesis is to solve a two-objective optimization problem in which the hovering-flight criterion is considered preponderant, but a new criterion that takes into account the forward-flight situation is also introduced, concurrently. The thesis work includes the set up of a hierarchy of models from low to high fidelity, in order to calibrate appropriate functional criteria. Secondly, our Nash game approach to competitive optimization will be implemented, using our optimization platform FAMOSA, and comparisons with the results by A. Dumont will be made.
Optimum design in naval hydrodynamics
Participants : Régis Duvigneau, Louis Blanchard.
Naval hydrodynamics field has recently shown a growing interest for optimum design methods. The computational context is especially complex because it implies unsteady two-phase turbulent flows, with possibly very high Reynolds number (up to ). The use of automated design optimization methods for such problems requires new developments to take into account the large CPU time necessary for each simulation and the specificity of the geometries considered.
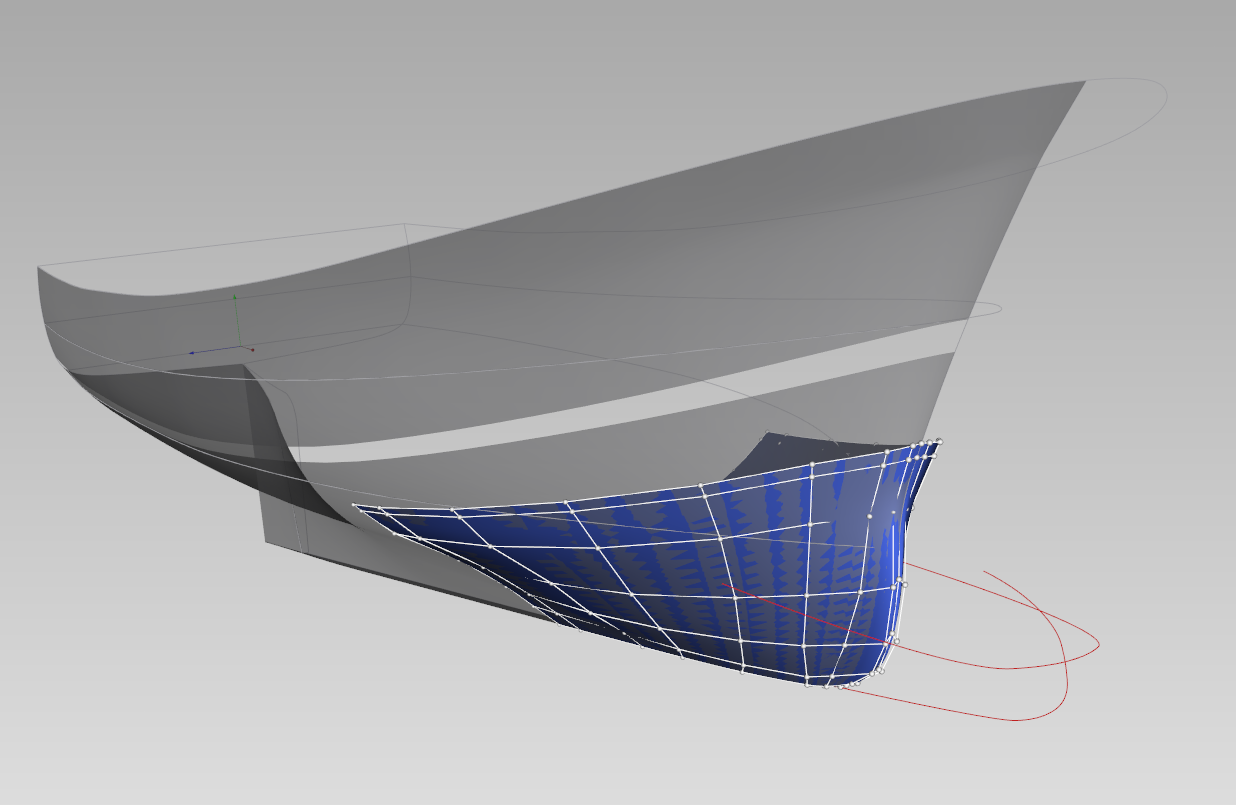
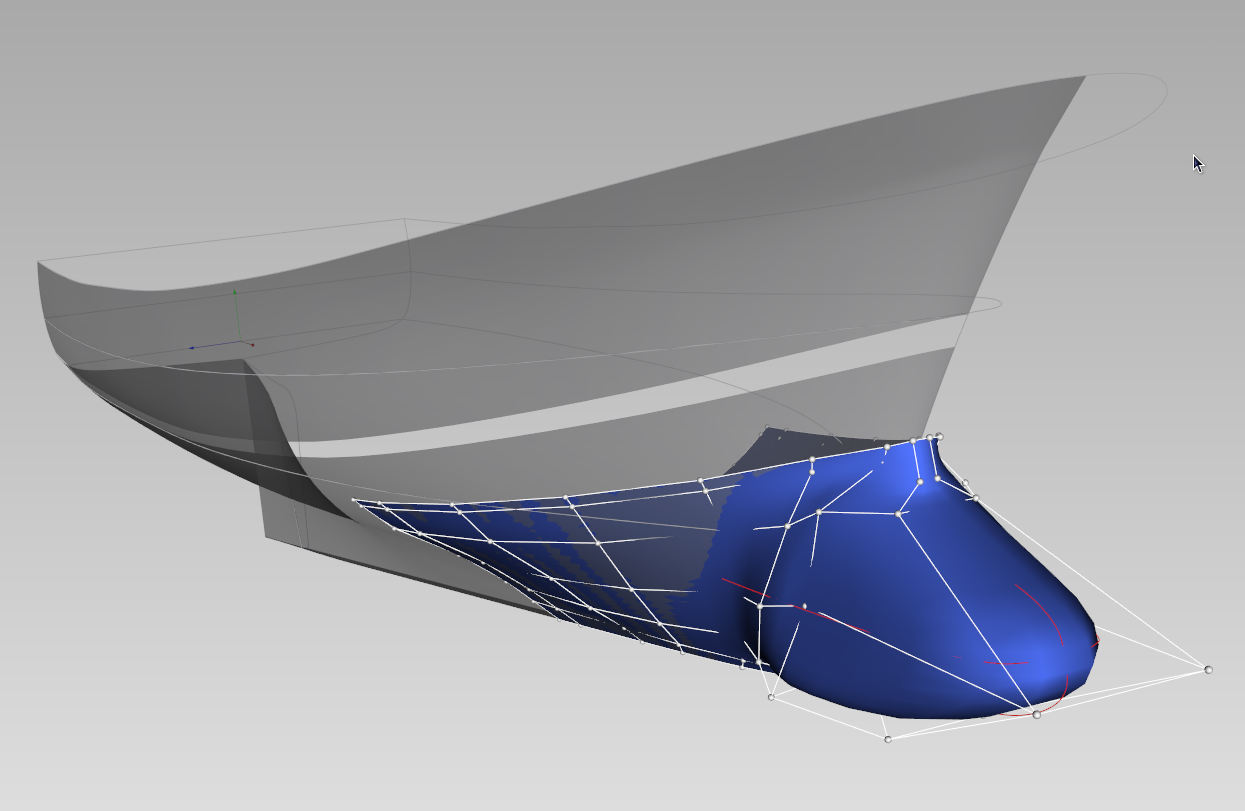
In collaboration with GALAAD Project-Team, some developments have been initiated on the geometrical modeling of hull shapes by parametric surfaces. The objective is to be able to modify existing hull shapes by controlling a small number of parameters, that are meaningful for naval architects. Two testcases are considered: the bow shape for trawler ships (see Fig. 4 ) and the whole hull shape for canoes, in collaboration with the Fédération francaise de Canoe-Kayak.