Section: New Results

Numerical methods for time domain wave propagation

High Order Theta Scheme for the linear wave equation.

Participants : Juliette Chabassier, Sébastien Impériale.

We have pursued our work about a new class of high order implicit three time step schemes for semi-discretized wave equations of the form

where $K_h$ is a symmetric positive definite matrix. For such problems, explicit three time step schemes generally show good performances but present two major drawbacks, in some situations, that have not yet been completely overcome:

• If the mesh presents elements of quite different sizes, the time step must be adapted to the smallest one because of the CFL condition.

• If the mass matrix is non diagonal or non block-diagonal, its inversion (at least one time per iteration) can lead to a dramatic over cost of the schemes, which is obviously not the case with implicit schemes for which a matrix has to be inverted in any case.

A natural way to avoid this restriction is to use local time stepping techniques which divides into two categories. First, the locally implicit technique, which is optimal in term of CFL restriction but “only” second order accurate in time, and requires the inversion of interface matrices. Second, the fully explicit local time stepping, as developed that enables to achieve high order time stepping but without (up to now) a full control over the CFL condition.

This is why we construct generalized implicit $\theta$-scheme using the modified equation approach to obtain 4th order approximation. These schemes introduce 2 degree of freedom $\theta$ and $\varphi$ and can be written under a general form as

The parameters $\theta$ and $\varphi$ are chosen as functions of the time step through the resolution of an optimization problem: we consider that the time step is given and we try to obtain a scheme that minimizes the consistency errors still being stable. The limit problem when the time step tends is infinite gives an optimal unconditionally stable fourth order scheme. This work has been submitted for publication.

Discontinuous Galerkin Methods for wave equations

Participants : Patrick Joly, Antoine Tonnoir.

This has been the subject of the internship of A. Tonnoir and can be seen as a contribution to the mathematical analysis of coupled BEM / DG methods for time domain diffraction problems (see section 6.1.4 ). We did not pretend to make a real contribution to the field of the analysis of DG methods, but wanted to understand in sufficient detail the quite surprising observation that the non-centered (in space) schemes, provided by the use of non centered fluxes in the DG approach, leads to a better accuracy than the centered schemes issued for central fluxes ! This has been done (for the simple 1D wave equation) from two points of view : the direct energy method and the Fourier analysis (or dispersion analysis) on regular grids.

Analysis of time domain boundary integral equations

Participants : Patrick Joly, Nicolas Le Guillarme.

This has been developed again as a part of the mathematical analysis of coupled BEM / DG methods for time domain diffraction problems (see section 6.1.4 ). With J. Rodríguez, we have revisited the analysis of the coercivity / continuity properties of space-time boundary integral associated to wave diffraction problem. Unlike the more traditional approach based on Laplace transform in time (cf the initial work by Bamberger-Ha Duong) we treat this question directly in the time domain by exploiting in a simple way the connection between integral equations and boundary value problems. This can be done in a very general setting but also particularized to the 1D case for which we got sharp estimates (internship of N. Le Guillarme). Furthermore, we can reinterpret the classical discretization by finite elements for retarded potentials as non conforming finite element methods. This allows to investigate in a new way the error analysis of time domain boundary element methods, which will be the subject of a future work.

Coupling Retarded Potentials and Discontinuous Galerkin Methods for time dependent wave propagation problems

Participant : Patrick Joly.

This topic is developed in collaboration with J. Rodriguez (Santiago de Compostela) in the framework of the contract ADNUMO with AIRBUS. Let us recall that our objective was to use time-domain integral equations (developed in particular at IMACS and EADS) as a tool for constructing transparent boundary conditions for wave problems in unbounded media. Our previous contribution of this topic concern the construction of an energy preserving method for the coupling space-time Galerkin approximation of the integral equations with discontinuous Galerkin finite elements and leap-frog time discretization for the numerical approximation of the equations inside the computational domain. For stability reasons, we had to use central fluxes. The drawback of central fluxes is that they do not lead to an optimal accuracy (see also the paragraph on the analysis of DG methods) which is traduced in practice by high frequency spurious oscillations.

Our objective this year was to look for another discretization approach that would overcome these problems. The approach we propose consists in playing on the time discretization procedure. For this we decompose the stiffness bilinear form as the sum of a conservative term corresponding to the use of central fluxes and a ("small") dissipative term due to off-centering and involving jumps across interfaces of the discrete solution. We propose a scheme which treats the conservative part of the equation in a centered way (leap-frog type) and the dissipative term in a non centered way ( backward Euler type). Doing so, the overall accuracy in time of the scheme is preserved (with respect to the case of central fluxes) and the stability is maintained at the price of a (slightly) more constraining CFL conditions, which does not seem that much penalizing for the application. The stability is analyzed through the decay of an discrete energy. As a consequence, we can adapt the discretization of the coupling terms between integral and interior equations in order to preserve the stability of the fully coupled scheme under the same CFL condition. Numerical validations are in progress.

Solving the Homogeneous Isotropic Linear Elastodynamics Equations Using Potentials and Finite Elements.

Participants : Eliane Bécache, Aliénor Burel, Sébastien Impériale, Patrick Joly.

This topic is the subject of the first part oh th PhD thesis of A. Burel and has been developed for a part in collaboration with Marc Duruflé. Decomposing the displacement field into potentials is a well-known tool in elastodynamics, and it expresses the decoupling of the pressure wave and the shear wave inside a homogeneous isotropic media. Although this tool is classically used when searching for analytic solutions, it does not seem to have been exploited for numerical computation using finite elements for instance. However, this is a priori attracting since, contrary to a displacement field approach for instance, it allows to decouple the approximation of P and S waves and to adapt the discretization process (mesh size, order of elements) to the dynamics of each type of wave, which is a priori particularly interesting when S-waves propagate much more slowly than P-waves (soft materials such as rubber). The main difficulty is to cope with the coupling of the different types of waves (the so-called conversion of modes) which occurs, due to wave reflections and transmissions, at interfaces between homogeneous media or at physical boundaries. The simplest situation where this phenomenon appears is the propagation of elastic waves in a homogeneous domain with clamped boundary. The main difficulty is to guarantee the stability of the treatment of the boundary condition. For this, we have proposed a variational formulation in which the stiffness bilinear form appears as a sum of a decoupled volumic bilinear form and a coupled surfacic bilinear form. This formulation is is compatible to an energy conservation result. After space discretization with finite elements spaces well adapted to each type of waves (using different meshes and / or polynomial degrees), we propose a discrete energy preserving numerical scheme, based on an explicit discretization of the volume terms and an implicit discretization of the surface terms. The resulting scheme is mainly explicit (only a sparse boundary linear system has to be solved at each time step) and stable under a CFL stability condition that is not affected by the presence of the boundary. An approach based on a modification of this scheme has been proposed for treating the free surface condition. This approach appears to give satisfactory results in the frequency domain (on the basis of numerical simulations) but fails in tim domain due to (apparently unconditional) instabilities.

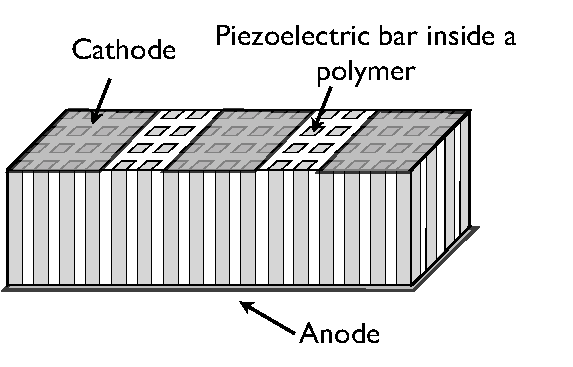
Mathematical and numerical modeling of piezoelectric sensors.

Participants : Sébastien Impériale, Patrick Joly.

This research, which constitutes the subject of the PhD thesis of S. Imperiale (which will be defended in January 2012) is developed in the framework of a collaboration with CEA-LIST about the numerical modeling of non-destructive testing experiments using ultrasonic waves.

More precisely, we have concerned during the past three years by mathematical and numerical questions related to the simulation of non destructive testing experiments using piezoelectric devices. In particular, we have investigated the modeling of piezoelectric sensors that are used to generate and record ultrasonic waves in a solid material : such waves are typically used to investigate in a non invasive way the possible presence of defects in manufactured items. Such an issue has already been tackled in the engineering literature but not, to our knowledge, by way of rigorous applied mathematics. As we are arriving at the conclusion of this work, let us summarize our main contributions during these three years (these have been published in M2AN)

• The full equations of piezoelectricity couple Maxwell's equations with linear elastodynamics equations which corresponds to a coupled hyperbolic system. This system presents quite different time scales due to the very large ratio between the speed of light and the sound speed, which makes it impossible to treat by a direct numerical approach. To overcome this problem, we have given a rigorous justification, via asymptotic analysis, of the so-called quasi-static approximation model in which the electric unknowns are reduced to a scalar electric potential : the reduced model appears as a coupled elliptic-hyperbolic system.

  $\begin{array}{cc}\rho {\partial }_{tt}u-\mathrm{𝐝𝐢𝐯}C\epsilon \left(u\right)-\mathrm{𝐝𝐢𝐯}𝐞\nabla \varphi =0\hfill & \text{in}{\Omega }_S\text{(the}\text{solid}\text{domain)},\hfill \\ \nabla ·ϵ\nabla \varphi -\nabla ·{𝐞}^T\epsilon \left(u\right)=0\hfill & \text{in}{ℝ}^3.\hfill \end{array}$

• We have next justified the reduction of the computation of this electric potential to the piezoelectric parts of the computational domain, considering the large contrast of permittivity between piezoelectric materials and surrounding polymers. This relies again on a limit process: the ratio between permittivities is the small parameter.

• A particular attention has to be devoted to the modeling of the electric supply process: more precisely the nonlocal (in space) boundary conditions on the electrodes (used to model the emission and reception regimes), as well as the modeling of the coaxial cable connecting the sensor to the electric generator (see also section 6.4.1 ).

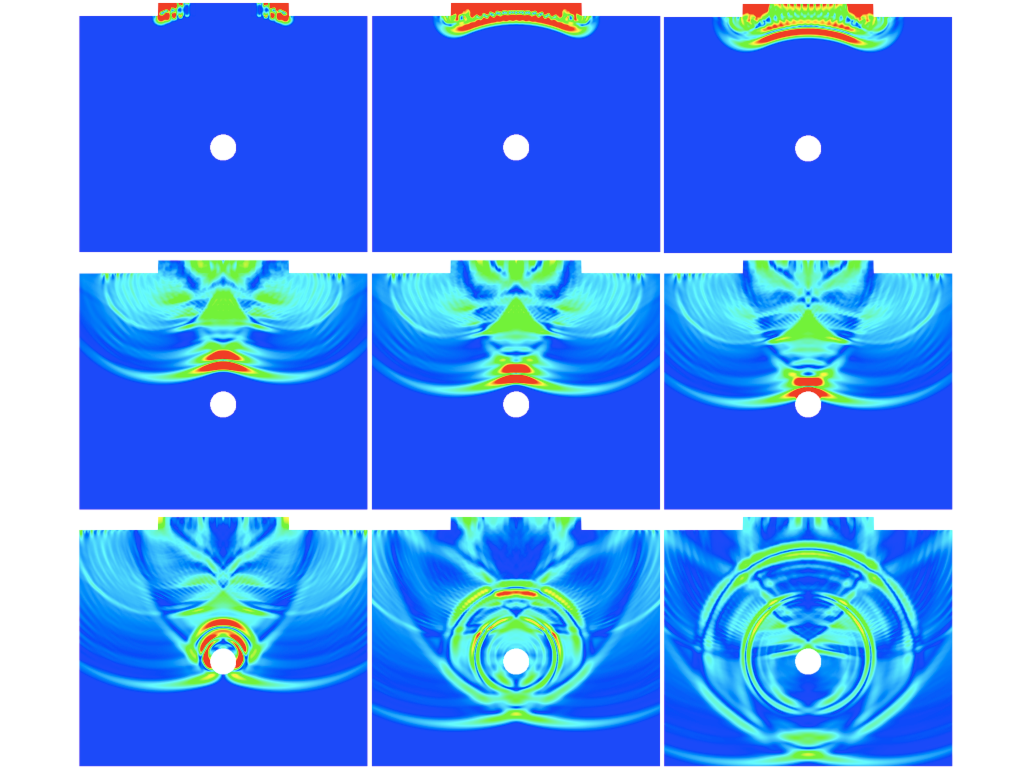
• Concerning the numerical approximation, an energy preserving finite element / finite differences numerical scheme is developed. A specific procedure is used for treating the nonlocal boundary conditions on the electrodes. Unbounded media have been treated via PML techniques that are dealt with using an original mortar element technique (see section 6.3.1 for more details). Various numerical results in academic or more realistic situations have been obtained. For instance, we have been able to model how one can exploit multi-component devices (see figure 1 ) to produce well focused waves (see figure 2 ).

• A computational code issued from our research, named Ondomatic (12 000 lines in C++), has been implemented. This code uses the finite element library FEMME (15 000 lines in C++) that essentially relies upon the use of spectral finite element on hexahedral meshes.

Figure 1.

Figure 2.

Maxwell's equations in Lorentz materials

Participants : Patrick Ciarlet, Patrick Joly, Valentin Vinoles.

This is the time-domain counterpart of the research done at Poems about metamaterials (see also the section 6.2.7 ) and has been the subject of the internship of V. Vinoles. Lorentz materials are particular non dissipative dispersive materials which behave as metamaterials (with negative index of refraction) in some range of frequencies. Their constitutive laws (links between electric and magnetic fields and the related inductions) are described in terms of ordinary differential equations (harmonic oscillators). We have studied Maxwell's equations in such materials and in particular proposed an energy preserving space-time discretization scheme based on an extension of classical methods (mixed finite elements in space, leap-frog type schemes in time). This has been implemented in a code including PMLs for the treatment of unbounded domains. Various numerical experiments have been performed. They illustrate the spectacular dispersive effects of Lorentz materials and allow us to recover the expected focalisation phenomena by an interface between a metamaterial and a standard dielectric one. This code will be an essential tool for the further investigation of more theoretical (and challenging) issues such as the limiting amplitude principle in this context.

Evolution problems in perturbed infinite periodic media

Participants : Julien Coatléven, Sonia Fliss.

First, as a part of the PhD of J. Coatléven, based on the former method to solve linear evolution problems in locally perturbed infinite periodic strips through the construction of transparent boundary conditions, a method has been developed to solve its natural geometric extension, i.e. the case of a locally perturbed line defect in an infinite periodic media. The method is again based on a semi-discretization in time of the problem on the whole infinite periodic media, and a generalization of the Lippmann-Schwinger equation approach we have developed for the treatment of this kind of geometries but for harmonic wave problems. At each time step, the solution is written as the sum of the solution of a time step in the unperturbed line defect and a contribution of the perturbation due not only to the current time step but also to all time steps involved in the numerical scheme. This intrication of time steps requires a careful treatment of the Lippmann-Schwinger equation, and in particular of the source term. Using the Floquet-Bloch transform, the computation of all the quantities involved can be reduced to the resolution of a few time steps of linear evolution problems in locally perturbed infinite periodic strips, where we can use the former method. As in the harmonic case, the discretization of the inverse Floquet-Bloch transform is done using appropriate quadrature rules, whereas the space discretization requires classical finite elements. The theoretical basis as well as the numerical analysis of this method are well understood, and the method has been successfully tested numerically. For instance, it can be shown, and checked numerically, that in the particular case of the wave equation, if one uses enough quadrature points (depending on the length of the time interval), then this quadrature creates no error of approximation.

For parabolic problems set in locally perturbed periodic media, we have developed another approach to determine the time-domain DtN operator. The principle is to apply the Laplace Transform in time to the equation and use the construction of the DtN operator for stationary equations. The main difficulty is the computation of the inverse of the Laplace Transform, more precisely to understand how to deal with the unbounded interval of integration and the choice of the discretization of the laplace variable. To deal with the first difficulty for waveguide problem, we have studied the asymptotic behavior of the DtN operator in the laplace domain when the laplace variable tends to $p_0\pm \infty$. To deal with the second difficulty, we have used the Z-Transformation and its properties. The numerical study is still in progress. This work enters in the framework of the ANR PRoject MicroWave (Sonia Fliss is an external collaborator), in collaboration with Karim Ramdani (Institut Elie Cartan de Nancy, UMR CNRS 7502), Christophe Besse and Ingrid Violet (Laboratoire Paul Painlevé, UMR CNRS 8524).

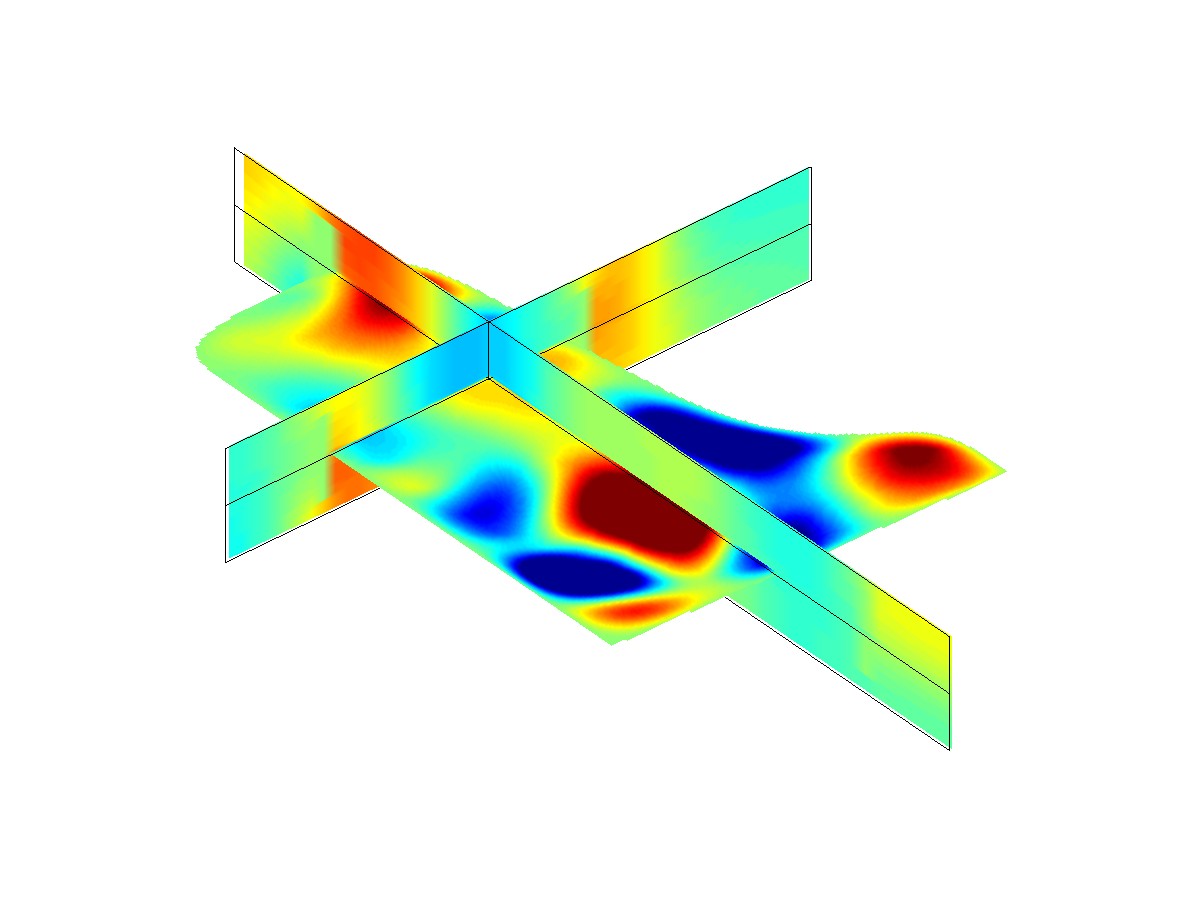
Modeling and numerical simulation of a piano.

Participants : Juliette Chabassier, Patrick Joly.

This work is developed in collaboration with Antoine Chaigne (UME, ENSTA). The purpose of this work the time domain modeling and numerical simulation of a piano. We aim at explaining the vibratory and acoustical behavior of the piano, by taking into account the main elements that contribute to sound production. The soundboard is modeled as a bidimensional thick, orthotropic, heterogeneous, frequency dependant damped plate, using Reissner Mindlin equations. The vibroacoustics equations allow the soundboard to radiate into the surrounding air, in which we wish to compute the complete acoustical field around the perfectly rigid rim. The soundboard is also coupled to the strings at the bridge, where they form a slight angle from horizontal. Each string is modeled by a one dimensional damped system of equations, taking into account not only the transversal waves excited by the hammer, but also the stiffness thanks to shear waves, as well as the longitudinal waves arising from geometric nonlinearities. The hammer is given an initial velocity that projects it towards a choir of strings, before being repelled. The interacting force is a nonlinear function of the hammer compression.

The final piano model that is discretized is a coupled system of partial differential equations, each of them exhibiting specific difficulties (nonlinear nature of the string system of equations, frequency dependant damping of the soundboard, great number of unknowns required for the acoustic propagation), in addition to couplings' inherent difficulties. On the one hand, numerical stability of the discrete scheme can be compromised by nonlinear and coupling terms. A very efficient way to guarantee this stability is to construct a numerical scheme which ensures the conservation (or dissipation) of a discrete equivalent of the continuous energy, across time steps. A major contribution of this work has been to develop energy preserving schemes for a class of nonlinear systems of equations, in which enters the string model. On the other hand, numerical efficiency and computation time reduction require that the unknowns of each problem's part, for which time discretization is specific, hence different, be updated separately. To achieve this artificial decoupling, adapted Schur complements are performed after Lagrange multipliers are introduced.

The potential of this time domain piano modeling is emphasized by realistic numerical simulations. Beyond greatly replicating the measurements, the program allows us to investigate the influence of physical phenomena (string stiffness or nonlinearity), geometry or materials on the general vibratory behavior of the piano, sound included. Spectral enrichment, << phantom partials >> and nonlinear precursors are clearly revealed when large playing amplitudes are involved, highlighting how this approach can help better understand how a piano works.

The main contributions of this year have been the following :

• to write the acoustic propagation as a first order system of equation, involving the physical sound pressure (as opposed to before, when its primitive had to be considered) and the acoustical velocity : this allowed us to artificially bound the computation domain with Perfeclty Matched Layers.

• to decrease the numerical computation times via a massive parallelization of the code : parallel modal search for the soundboard, parallel dense matrix-vector product for the vibroacoustic equations in the modal basis, parallel resolution of the 3D acoustic propagation, multi-threaded computation of the strings' problem.

• to perform realistic computations, which have provided physically relevant numerical simulations (see Figure 3 ).

Several measurements have also been conducted on a grand piano in order to provide realistic values of parameters and calibrated data to compare simulation with.

Figure 3.