Section: New Results

Synthesis of compact multiplexers and de-embedding of multiplexers

Participants : Martine Olivi, Sanda Lefteriu, Fabien Seyfert.

This work has been done in collaboration with Stéphane Bila (Xlim, Limoges, France), Hussein Ezzedin (Xlim, Limoges, France), Damien Pacaud (Thales Alenia Space, Toulouse, France), Giuseppe Macchiarella (Politecnico di Milano, Milan, Italy, and Matteo Oldoni (Politecnico di Milano, Milan, Italy).

Synthesis of compact multiplexers

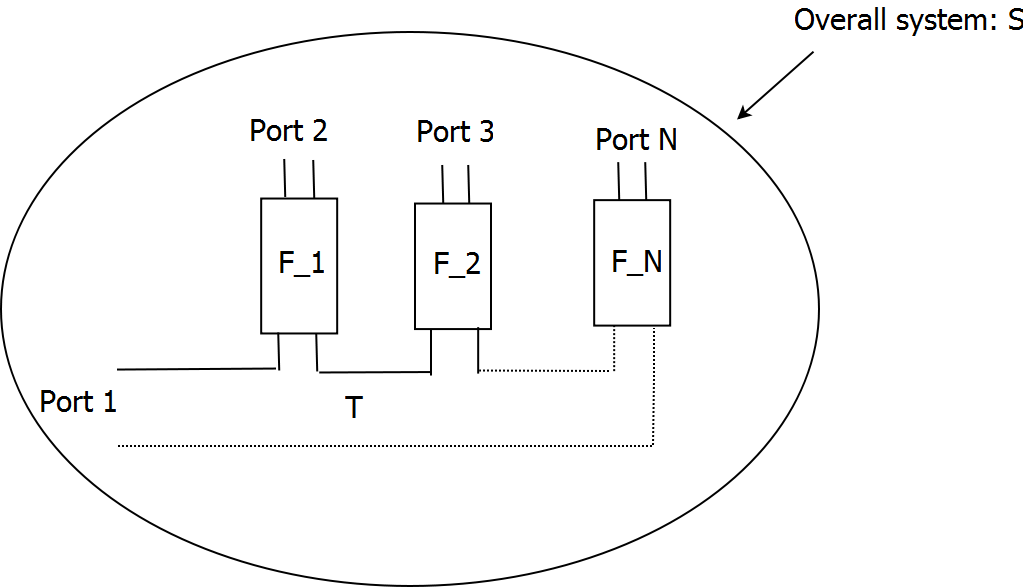
We focused our research on multiplexer with a star topology. These are comprised of a central $N$-port junction, and of filters plugged on all but common ports (see Figure 9 ). A possible approach to synthesis of the multiplexer's response is to postulate that each filter channel has to match the multiplexer at $n_k$ frequencies ($n_k$ being the order of the filter) while rejecting the energy at $m_k$ other frequencies ($m_k$ being the order the transmission polynomial of the filter). The desired synthesis can then be cast into computing of a collection of filter's responses matching the energy as prescribed and rejecting it at specified frequencies when plugged simultaneously on the junction. Whether such a collection exists is one of the main open issues facing co-integration of systems in electronics. Investigating the latter led us to consider the simpler problem of matching a filter, on a frequency-varying load, while rejecting energy at fixed specified frequencies. If the order of the filter is $n$ this amounts to fix a given transmission polynomial $r$ and to solve for a unitary polynomial $p$ meeting interpolation conditions of the form:

where $q$ is the unique monic Hurwitz polynomial satisfying the Feldtkeller equation

This problem can be seen as an extended Nevanlinna-Pick interpolation problem, which was considered in [62] when the interpolation frequencies lie in the open left half-plane. We conjecture that existence and uniqueness of the solution still holds in our case, where interpolation takes place on the boundary, provided $r$ has no roots on the imaginary axis. Numerical experiments based on continuation techniques tend to corroborate our belief: efforts now focus on a mathematical proof. The derived numerical tools have already been used to successfully to design multiplexer's responses in collaboration with CNES and Xlim, thereby initiating a collaboration with Xlim on co-integration of filters and antennas.

De-embedding of multiplexers

Let $S$ be the measured scattering matrix of a multiplexer composed of a $N$-port junction with response $T$ and $N-1$ filters with responses $F_1,\cdots F_{N-1}$ as plotted on Figure 9 . The de-embedding question we raise is the following: given $S$ and $T$, is it possible to retrieve the $F_k$'s ? The answer to this question depends of course of the admissible class of filters. For the simplest case where no assumption is made (except reciprocity), we showed that the problem has a unique solution for $N>3$ and for generic $T$, while for $N=2$ the solution space at each frequency point has real dimension 2. This redundancy can be explained by the existence of "ghost" or "silent" components that can hide behind the junction: when being chained to the junction these components do not affect its response. We also experienced that the generic behaviour for $N>3$ is rather theoretical, as usual junctions are often made of chained T-junctions: in this non generic case (which is rather generic in practice !) some "silent" component still exists for $N>3$. Additional hypotheses, such as rationality with prescribed degree for $F_k$, are currently being studied and already yielded results for the case $N=3$ [21] .

This work is pursued in collaboration with Thales Alenia Space, Politecnico di Milano, Xlim and CNES in particular within the contract CNES-Inria on compact $N$-port synthesis (see section 7.1 ).

Figure 9. Multiplexer made of a junction $T$ and filtering devices $F_1,F_2\cdots F_N$