Section: New Results

Edges, transitions and criticality

Participants : Suman Maji [correspondant] , Hussein Yahia.

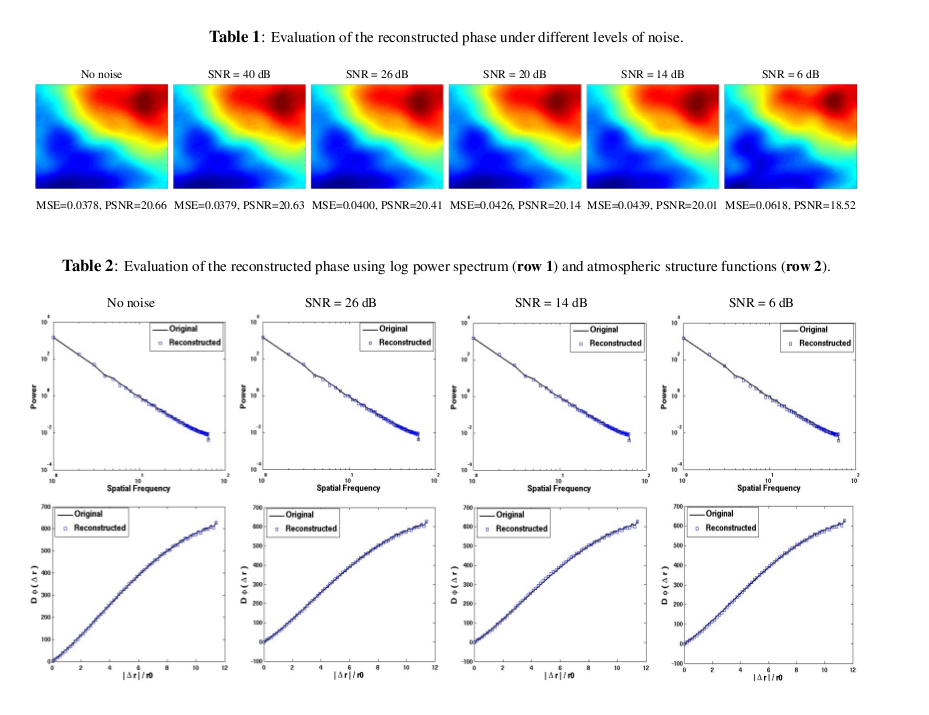
In this work, various notions of edges encountered in digital image processing are reviewed in terms of compact representation (or completion). We show that critical exponents defined in Statistical Physics lead to a much more coherent definition of edges, consistent across the scales in acquisitions of natural phenomena, such as high resolution natural images or turbulent acquisitions. Edges belong to the multiscale hierarchy of an underlying dynamics, they are understood from a statistical perspective well adapted to fit the case of natural images. Numerical computation methods for the evaluation of critical exponents in the non-ergodic case are recalled, which apply for the vast majority of natural images. We study the framework of reconstructible systems in a microcanonical formulation, show how it redefines edge completion, and how it can be used to evaluate and assess quantitatively the adequation of edges as candidates for compact representations. We study with particular attention the case of turbulent data, in which edges in the classical sense are particularly challenged. Tests are conducted and evaluated on a standard database for natural images. We test the newly introduced compact representation as an ideal candidate for evaluating turbulent cascading properties of complex images, and we show better reconstruction performance than the classical tested methods. See figure 8 .

Figure 8. From left to right in each line: an original input image, and the reconstruction performed on the outputs resulting from various edge detection algorithms, showing the superiority of edge pixels computed from the Microcanonical Multiscale Formalism (column MSM). Note that NLFS  [32] , which is based on nonlinear filtering, performs the best after MSM.

Figure 9. Results showing the robustness of the multiscale phase reconstruction algorithm for Adaptive Optics (AO) under various conditions of noise.