Section: New Results
Stability and control design of asynchronous interconnected systems
New approaches for stability analysis of time-delay systems
Participants : A. Seuret [Contact person] , F. Gouaisbaut.
A particular attention has been paid to the stability analysis of time delay systems. Indeed delays represent a classical phenomenon which appears in networked control systems cite. This corresponds to the fact that data are not transmitted instantaneously from one node to its neighbors. In this context some effort has been provided in order to reduce the conservatism of the stability conditions. This works represents some fundamental researches to develop accurate stability conditions to networked control systems. More especially we produced a paper [45] which addresses the stability problem of linear time delay system. In the literature, the most popular approach to tackle this problem relies on the use of Lyapunov-Krasovskii functionals. Many results have proposed new functionals and techniques for deriving less and less conservative stability conditions. Nevertheless, all these approaches use the same trick, the well-known Jensen's inequality which generally induces some conservatism difficult to overcome. In light of those observations, we propose to reduce the conservatism of Lyapunov-Krasovskii functionals by introducing new classes of integral inequalities called Wirtinger's inequalities. This integral type inequality is firstly shown to encompass Jensen's inequality and is then employed to derive new stability conditions. To this end, a slightly modified Lyapunov functional is proposed. Several examples illustrate the effectiveness of our methodology. Further efforts on this topics have been provided and several improved articles are now submitted to servals journals.
Stability and control of asynchronous sampled-data systems
Participants : A. Seuret [Contact person] , C. Briat [ETHZ] , J. Gomes Da Silva Jr. [UFRGS] , M. M. Peet [Illinois Institute of Technology] .
Sampled-data systems have been extensively studied in the literature and the references therein. It is now reasonable to design controllers which guarantee the robustness of the solutions of a closed-loop system under periodic samplings. However the case of asynchronous samplings still leads to several open problems. This corresponds to the realistic situation where the difference between two successive sampling instants is time-varying. Several articles drive the problem of time-varying periods based on a discrete-time approach, input delay approach using the framework of Lyapunov-Krasovskii theorem, using the small gain theorem or the analysis of impulsive systems. These last approaches are very relevant to this problem because they cope with time-varying sampling periods as well as with uncertain systems in a simple manner. Nevertheless, these sufficient conditions are still more conservative than discrete-time approaches. In [24] , we proposed a novel approach to assess stability of continuous linear systems with sampled-data inputs. The method, which is based on a particular type of functionals, called `looped-functionals' provided easy tractable stability conditions for the continuous-time model. This method has been extended to various cases dealing with sampled-data systems. Indeed a method to constructs such class of functionals using the Sum of Squares framework was developed in [23] . Another extensions was also proposed in order to include saturations in the actuators [21] . Extensions to the case of communication delays and asynchronous samplings was also provided in [22] .
Based on this new type of Lyapunov functional, several works have been provided in the more general context of hybrid system. Indeed sampled-data systems can be seen as a particular type of hybrid systems. This has been provided in several study done by A.R. Teel, Dragan Nesic and many other researchers. Thus the idea was to show that the previous approach was also able to provide efficient stability conditions for impulsive systems [16] , [27] , [28] , [54] or switched systems [53] .
Event-based control
Participants : A. Seuret [Contact person] , N. Marchand [Gipsa-Lab] , C. Prieur [GIPSA-Lab] , S. Durand [CINVESTAV] .
Usually feedback laws are implemented in a periodic fashion on digital hardware. The main reason for using this periodicity in the hardware comes from the difficulties to analyze the stability of aperiodic or asynchronous systems. However it also seems natural to hold the same control input longer if the system behaves in a suitable way or shorter if the system requires an updated input. In [9] , an algorithm is suggested to sample the control input based on the behavior of a Lyapunov-like function. This algorithm is called event-triggered since the Lyapunov-like function directly depends on the state of the systems. Using a Lyapunov-like function, two algorithms for the design of event-triggered algorithm are designed. It is assumed that a stabilizing controller for the continuous control system is given. Both event-triggered algorithms need to consider a closed-loop system with a mixed discrete/continuous dynamics (namely this is a hybrid system). Some numerical simulations illustrate the stability properties of both algorithms. In a future work, the performance issue should be analyzed. It is remarked that the event-triggered algorithms have a different performance. The first one seems to ensure a good speed of convergence on numerical simulations, whereas the second event-triggered algorithm allows less jumps and thus needs to compute less often the control variables. The advantages and disadvantages of each algorithm will be studied more precisely in a future work, for a theoretical point of view (e.g. by estimating a priori the number of switches), or on applications (to understand which algorithm is better depending on the application). Regarding this remark a journal paper has been submitted to IMA Journal of Mathematic Control and Information lately in 2012.
Feedback under slacken real-time
Participants : D. Simon [Contact person] , A. Seuret, P. Andrianiaina [AIRBUS] .
Robustness in control usually deals with the plant's parameter uncertainties, but the insensitivity or adaptability w.r.t. timing deviations from the theoretical pattern, such as jitter or deadlines misses can be exploited. The interesting point is that a feedback control system which is robust w.r.t. the plants parameters uncertainties is also robust, to some extent, w.r.t. timing deviations. Hence a feedback control system is not as hard as it is often considered in the literature, but should be better considered as weakly hard, i.e. able to tolerate specified timing deviations without leaving its requested performance [46] .
A weakened implementation scheme for real-time feedback controllers is proposed to reduce the conservatism due to traditional worst-cases considerations. To save wasted computing resources, new real-time scheduling scenarios allowed for reducing the time slots allocated to control tasks below the value of the Worst Case Execution Time which is traditionally used to implement embedded control software. The stability of the control system under occasional deadlines miss is assessed using robustness arguments, using Lyapunov-Krasovskii functionals and LMIs solving based on [10] . The methodology has been successfully assessed for a fighter aircraft pitch controller, which show that the stability of the plant can be kept (and even improved) using the new scheduling schemes using less computing resources than traditional implementations [25] , [11] .
Varying sampling for LPV systems
Participants : D. Simon [Contact person] , O. Sename, E. Roche.
In the context of network-controlled systems the idea of using varying control intervals naturally arises when the available computing power devoted to feedback control is limited, e.g. in embedded systems. It can be easily shown that decreasing the control frequency directly decreases the amount of computing needed for control. However, the stability of the feedback controller under varying sampling must be assessed for all the allowed variations of the sampling intervals [8] .
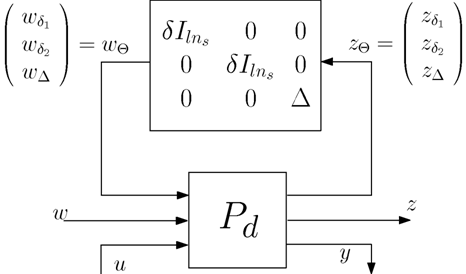
The Linear Fractional Transform (LFR) formulation is widely used in robust analysis to study the influence of the plant's uncertain parameters on the stability and performances of a closed-loop system. Usually it is used to build a parameter dependent model of a dynamical system, depending on a known set of parameters. Here the set of varying parameters has been extended with the sampling interval of the control system, thus allowing to handle both varying sampling and plants uncertainties in a single framework (Figure 6 ).
Here, is a on-line discretized model of the plant, represents the uncertain parameters of the plant and is the variation of the sampling interval around its nominal value. From this model a robust controller can be synthesized, enforcing the control system stability for all variations of the sampling interval inside a predefined range.
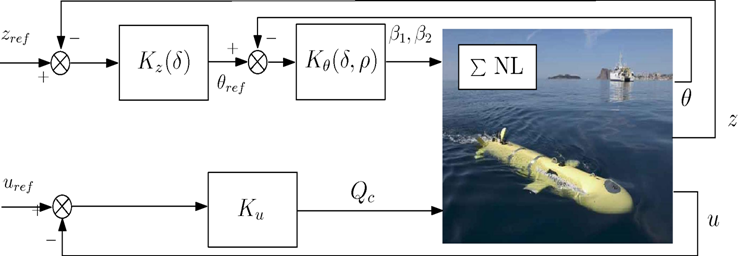
The approach have been successfully applied to the pitch and altitude control of a non-linear autonomous underwater vehicle, where the source of sampling variations comes from the altitude ultrasonics sensors [43] . However the approach still suffers from conservatism for which improvements using full block multipliers, or parameter-dependent Lyapunov functions, have been investigated [58] .