Section: Scientific Foundations
Multi-disciplinary nature of the project
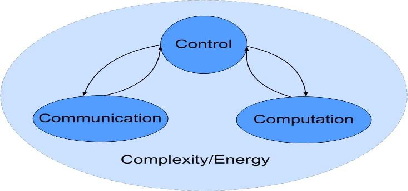
The team's project is to investigate problems in the area of NCS with the originality of integrated aspects on computation, communication and control. The combination of these three disciplines requires the interplay of the multi-disciplinary fields of: communication, real-time computation, and systems theory (control). Figure 2 , shows the natural interaction between disciplines that concern the NeCS project. The arrows describe the direction in which these areas interact, i.e.
Complexity and energy-management are additional features to be considered as well. Complexity here refers to the problems coming from: wireless networks with varying interconnection topologies, multi-agent systems coordination, scaling with respect to a growing number of sensors. Energy management concerns in particular the efficient handling of energy in wireless sensors, and means an efficient way to handle both information transmission and computation.
(a) Control in Communication
This topic is the study of how control-theoretic methods can be applied in order to solve some problems found in the communication field. Examples are: the Power control in cell telephones, and the optimal routing of messages in communication networks (Internet, sensor networks).
(b) Communication in Control
This area concerns problems where communication and information theory interact with systems theory (control). As an example of a classical paradigm we can mention the stabilization problem under channel (communication) constraints. A key result here [75] was to show that it was generically impossible to stabilize a linear system in any reasonable sense, if the feedback channel's Shannon classical capacity was smaller than the sum of the logarithms, base 2, of the unstable eigenvalues. In other words, in order to be able to cope with the stabilization problem under communication constraints, we need that
where the are unstable eigenvalues of the open loop system. Intuitively, this means that the rate of information production (for discrete-time linear systems, the intrinsic rate bits/time equals ) should be smaller than the rate of information that can be transmitted throughout the channel. In that way, a potentially growing signal can be cached out, if the information of the signal is sent via a channel with fast enough transmission rate. In relation to this, a problem of interest is the coding and control co-design. This issue is motivated by applications calling for data-compression algorithms aiming at reducing the amount of information that may be transmitted throughout the communication channel, and therefore allowing for a better resource allocation and/or for an improvement of the permissible closed loop system bandwidth (data-rate). Networked controlled systems also constitute a new class of control systems including specific problems concerned by delays. In NCS, the communication between two agents leads unavoidably to transmission delays. Also, transmission usually happens in discrete time, whereas most controlled processes evolve in continuous time. Moreover, communication can induce loss of information. Our objectives concern the stabilization of systems where the sensor, actuator and system are assumed to be remotely commissioned by a controller that interchanges measurements and control signals through a communication network. Additional dynamics are introduced due to time-varying communication delays, asynchronous samplings, packets losses or lack of synchronization. All those phenomena can be modeled as the introduction of time-delays in the closed loop system. Even if these time-delay approaches can be easily proposed, they require careful attention and more complex analysis. In general, the introduction of delays in a controlled loop leads to a reduction of the performance with respect to the delay-free situation and could even make the systems unstable. Our objective is to provide specific modeling of these phenomena and to develop dedicated tools and methodologies to cope with stability and stabilization of such systems.
(c) Computation in Control
This area concerns the problem of redesigning the control law such as to account for variations due to the resource allocation constraints. Computation tasks having different levels of priority may be handled by asynchronous time executions. Hence controllers need to be re-designed as to account for non-uniform sampling times resulting in this framework. Questions on how to redesign the control laws while preserving its stability properties are in order. This category of problems can arise in embedded systems with low computation capacity or low level resolution.
(d) Control in Computation
The use of control methods to solve or to optimize the use of computational resources is the key problem in this area. This problem is also known as a scheduling control. The resource allocations are decided by the controller that tries to regulate the total computation load to a prefixed value. Here, the system to be regulated is the process that generates and uses the resources, and not any physical system. Hence, internal states are computational tasks, the control signal is the resource allocation, and the output is the period allowed to each task.
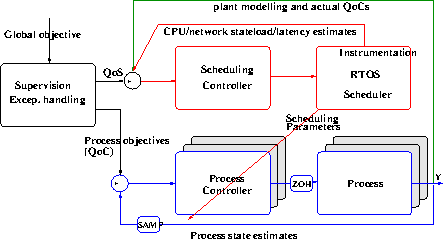
(c + d) Integrated control/scheduling co-design
Control and Computation co-design describes the possibility to study the interaction or coupling between the flows and . It is possible, as shown in Fig. 3 , to re-frame both problems as a single one, or to interpret such an interconnection as the cascade connection between a computational system, and a physical system. In our framework the feedback scheduling is designed w.r.t. a QoC (Quality of Control) measure. The QoC criterion captures the control performance requirements, and the problem can be stated as QoC optimization under constraint of available computing resources. However, preliminary studies suggest that a direct synthesis of the scheduling regulator as an optimal control problem leads, when it is tractable, to a solution too costly to be implemented in real-time applications [64] . Practical solutions will be found in the currently available control theory and tools or in enhancements and adaptation of current control theory. We propose in Fig. 3 a hierarchical control structure: besides the usual process control loops we add an outer control loop whose goal is to manage the execution of the real-time application through the control of the scheduling parameters of the inner loops. Together with the outer loop (working on a periodic sampled time scale) we also need a scheduling manager working on a discrete events time scale to process exception handling and admission control. The task periods directly affect the computing load, they have been chosen as actuators. They can be implemented through software variable clocks. As timing uncertainties cannot be avoided and are difficult to model or measure, we currently design robust control algorithms using the control theory, which have been successfully simulated and experimentally validated [74] . This methodology is supported by the software Orccad (see Section 5.1 ) where a run-time library for multi-rate multitasking has been developed and integrated. It will be further improved using a QoS-based management of the timing constraints to fully benefit from the intrinsic robustness of closed loop controllers w.r.t. timing uncertainties.