Section: New Results

Synthesis of compact multiplexers and de-embedding of multiplexers

Participants : Martine Olivi, Sanda Lefteriu, Fabien Seyfert.

This work has been done in collaboration with Stéphane Bila (XLIM, Limoges, France), Hussein Ezzedin (XLIM, Limoges, France), Damien Pacaud (Thales Alenia Space, Toulouse, France), Giuseppe Macchiarella (Politecnico di Milano, Milan, Italy), and Matteo Oldoni (Siae Microelettronica, Milan, Italy).

Synthesis of compact multiplexers

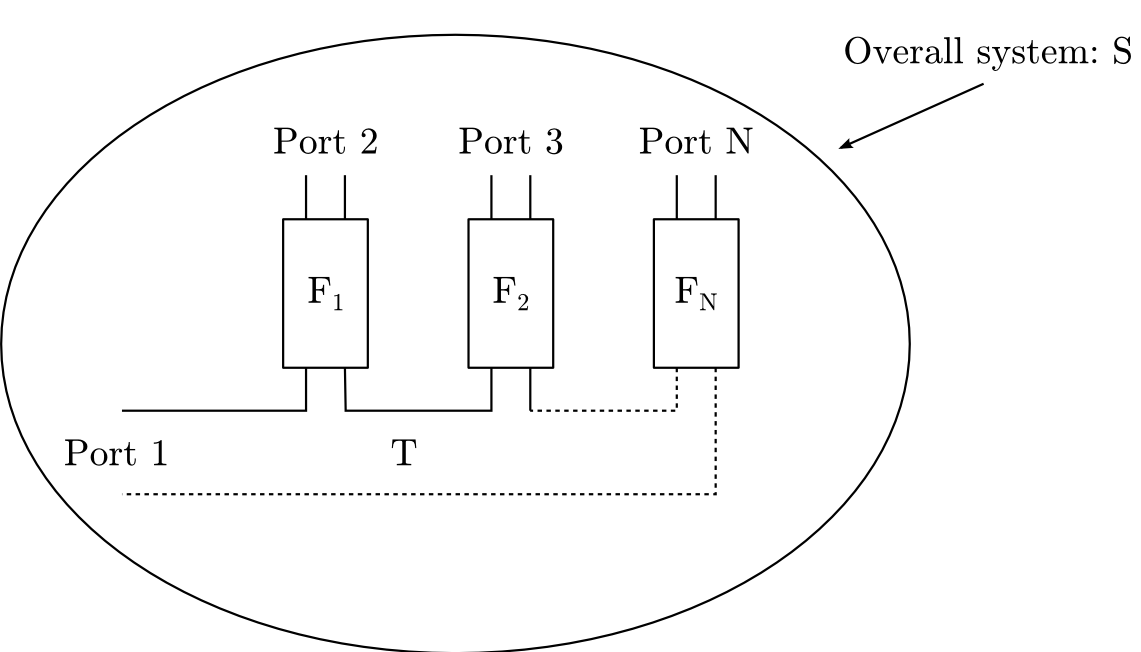
We focused our research on multiplexer with a star topology. These are comprised of a central $N$-port junction, and of filters plugged on all but common ports (see Figure 9 ). A possible approach to synthesis of the multiplexer's response is to postulate that each filter channel has to match the multiplexer at $n_k$ frequencies ($n_k$ being the order of the filter) while rejecting the energy at $m_k$ other frequencies ($m_k$ being the order the transmission polynomial of the filter). The desired synthesis can then be cast into computing of a collection of filter's responses matching the energy as prescribed and rejecting it at specified frequencies when plugged simultaneously on the junction. Whether such a collection exists is one of the main open issues facing co-integration of systems in electronics. Investigating the latter led us to consider the simpler problem of matching a filter, on a frequency-varying load, while rejecting energy at fixed specified frequencies. If the order of the filter is $n$ this amounts to fix a given transmission polynomial $r$ and to solve for a unitary polynomial $p$ meeting interpolation conditions of the form:

where $q$ is the unique monic Hurwitz polynomial satisfying the Feldtkeller equation

This problem can be seen as an extended Nevanlinna-Pick interpolation problem, which was considered in [65] when the interpolation frequencies lie in the open left half-plane. Last year we conjectured the existence and uniqueness of a solution, which were eventually proved true this year when $r$ has no roots on the imaginary axis. We already communicated on the subject ( 9.1 ), and a scientific report as well as an article are being written on this result [30] . The proof relies on the local invertibility of an evaluation map that is established using a differential argument and the structure of particular Pick matrices. The case where $r$ has zeros on the imaginary axis is of great interest, and though existence then holds again uniqueness is still not well-understood: it is conjectured that under minor restrictions on the localization of the ${\gamma }_k^{\text{'}}s$ (typically off an algebraic subvariety) the main results still hold.

This research lies at heart of our collaboration with CNES on multiplexer synthesis and the core of the starting ANR project COCORAM on co-integration of filters and antennas (see Section  8.1.1 ).

De-embedding of multiplexers

Let $S$ be the external scattering parameters of a multiplexer composed of a $N$-port junction with response $T$ and $N-1$ filters with responses $F_1,\cdots F_{N-1}$ as plotted on Figure 9 . The de-embbeding problem concerns the recovery of the $F_k$ and can be considered under different hypotheses. Last year we studied the de-embedding problem where $S$ and $T$ are known [76] but no particular structure on the $F_k$ is assumed. It was shown that for a generic junction $T$ and for $N>3$ the de-embedding problem has a unique solution. It was however observed that in practice the junction's response is far from being generic (as it is usually obtained by assembly of smaller $T$-junctions) which renders the problem extremely sensitive to measurement noise. It was also noticed that in practical applications, scattering measurements of the junction are hardly available.

It was therefore natural to consider following de-embedding problem. Given $S$ the external scattering measurement of the multiplexer, and under the assumptions:

• the $F_k$ are rational of known McMillan degree,

• the coupling geometry of their circuital realization is known,

what can be said about the filter's responses ? It was shown that under the above hypotheses, in particular with no a priori knowledge of $T$, the filter's responses are identifiable up to a constant chain matrix chained at their second port (nearest to the junction) [24] . It was also shown that this uncertainty bears only on the resonant frequency of the last cavity of each filter, as well as on their output coupling. Most of the filters' important parameters can therefore be recovered. The approach is constructive and relies on rational approximation of certain external scattering parameters, and on an extraction procedure similar to Darlington's synthesis for filters. Software developments have been pursued to implement the latter and practical studies are under way with data furnished by Thales Alenia Space and by Siae Microelettronica. A medium term objective is to extend the Presto-HF ( 5.3 ) software to de-embedding problems for multiplexers and more general multi-ports.

This work is pursued in collaboration with Thales Alenia Space, Siae Microelettronica, XLIM and CNES in particular under contract with CNES on compact $N$-port synthesis (see Section  7.1 ).