Section: New Results
3D reconstruction in fluorescence imaging
Participants : Emmanuel Soubies, Laure Blanc-Féraud, Sébastien Schaub.
This work was made in collaboration with Gilles Aubert, Laboratoire J.A. Dieudonné (CNRS,UNS).
We propose a new model for the reconstruction of biological structures using Multiple-Angle Total Internal Reflection Fluorescence Microscopy (MA-TIRFM). This recent microscopy technique allows the visualization of sub-cellular structures around the plasma membrane which is of fundamental importance in the comprehension of exchanges mechanisms of the cell. We present a 3D reconstruction method based on a shape prior information on the observed structures and robust to shot noise and background fluorescence. A novelty with respect to the state of the art is to propose a method allowing the recovery of multiple objects aligned along the axial axis.
TIRFM principle is based on the total internal reflection phenomenon of a light beam at the interface between two mediums of refractive indices (incident) and (transmitted) which produces an evanescent wave capable of exciting fluorophores that are near the coverslip surface. Excited fluorophores emit photons that are then collected by a CCD camera to produce a resulting 2D image (radial dimension). The 2D image formation is formulated as follows [29] :
where is the recorded image for the incident angle , denote the 3D unknown fluorophore density, is the intensity at the interface is the penetration depth (theoretically known) and is the incident light wavelength. The problem is then to determine in (1 ) from acquisitions with different incident angles.
In order to solve this ill-posed inverse problem, we model the 3D unknown fluorophore density by a collection of parametrized objects defined on a state space by their location and their marks (i.e geometric attributes ). The optimization problem can be formulated as a minimization problem where both the number of objects in the model and their parameters have to be estimated. This difficult combinatorial optimization problem is tackled by using a Marked Point Process approach [36] which allows modelling interactions between the objects in order to regularize the inverse problem.
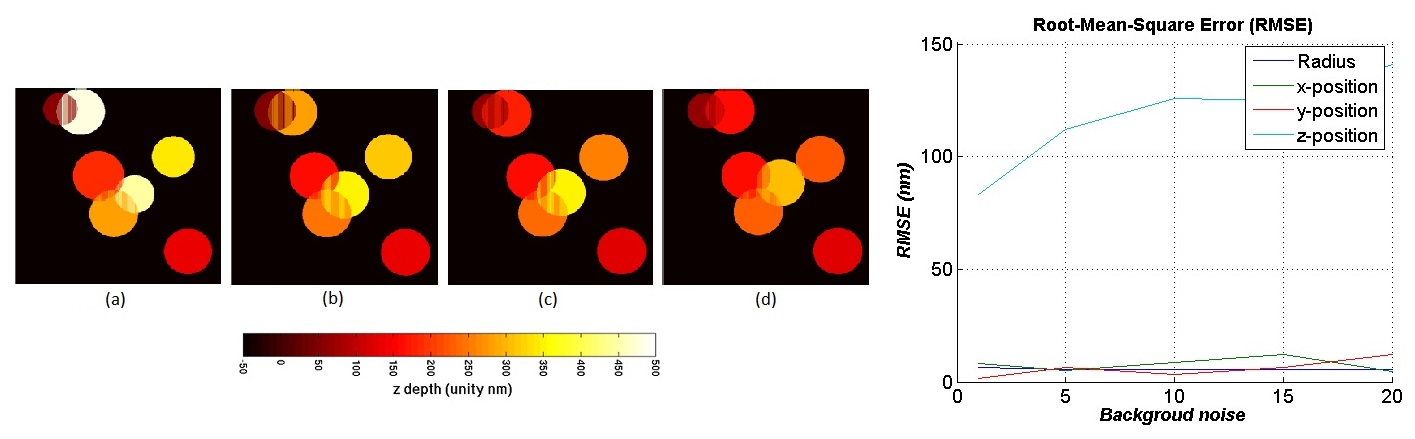
Figure 1 right shows the Root Mean Square Errors (RMSE) of each estimated parameter for different noise levels on simulated data. We obtain a hight accuracy reconstruction with an RMSE less than for the radial position (x,y) and the radius. A larger RMSE (between 80 and , depending on the noise level) is found on the axial position vesicles estimation. As we can see on figure 1 left, the error on the axial position estimation is due to the deepest objects (), objects close to the glass interface are well estimated. Figure 1 right shows also the robustness of the model with respect to shot noise and background fluorescence since the errors remain almost constant with the increasing noise level. The proposed method have also been tested on a real sample of beads of known diameters in order to quantify the quality of the reconstruction. The obtained results are promising for feature estimation of predefined shape structures [17] .