Section: New Results

A Hierarchical, Graph-cut-based Approach for Extending a Binary Classifier to Multiclass – Illustration with Support Vector Machines

Participants : Alexis Zubiolo, Eric Debreuve, Grégoire Malandain.

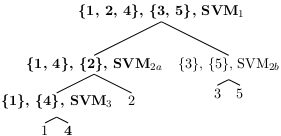
The problem of automatic data classification is to build a procedure that maps a datum to a class, or category, among a number of predefined classes. The building of such a procedure is the learning step. Using this procedure to map data to classes is referred to as classification or prediction. The procedure is therefore a classification, or prediction, rule. A datum (text document, sound, image, video, 3-dimensional mesh...) is usually converted to a vector of real values, possibly living in a high-dimensional space, also called signature. Offline, supervised learning relies on a learning set and a learning algorithm. A learning set is a set of signatures that have been tagged with their respective class by an expert. The learning algorithm input is formed by this set together with some parameters, its output being a prediction rule. Some learning algorithm, or method, apply only to the 2-class case. Yet, adapting such a binary classifier to a multiclass context might be preferred to using intrinsically multiclass algorithms, for example if it has strong theoretical grounds and/or nice properties; if free, fast and reliable implementations are available...The most common multiclass extensions of a binary classifier are the one-versus-all (OVA) (or one-versus-rest) and one-versus-one (OVO) approaches. In any extension, several binary classifiers are first learned between pairs of groups of classes. Then, all or some of these classifiers are called when predicting the classes of new samples. When the number of classes increases, the number of classifiers involved in the learning and the prediction steps becomes computationally prohibitive. Hierarchical combinations of classifiers can limit the prediction complexity to a logarithmic law in the number of classes (at best). Combinatorial approaches can be found in the literature. Because of their high learning complexity, these approaches are often disregarded in favor of an approximation trading optimality for computational feasibility. In our work, the high combinatorial complexity is overcome by formulating the hierarchical splitting problems as optimal graph partitionings solved with a minimal cut algorithm. In fact, as this algorithm performs only few additions and comparisons, its impact on the whole procedure is not significant. A modified minimal cut algorithm is also proposed in order to encourage balanced hierarchical decompositions (see Fig. 11 ). The proposed method is illustrated with the Support Vector Machine (SVM) as the binary classifier. Experimentally, it is shown to perform similarly to well-known multiclass extensions while having a learning complexity only slightly higher than OVO and a prediction complexity ranging from logarithmic to linear. This work has been accepted to the International Conference on Computer Vision Theory and Application (VISAPP 2014) [20] .

Figure 11. Type of tree that the proposed method builds during the learning stage (illustration with 5 classes). An example of classification of a new image signature is also illustrated by showing the visited nodes in boldface (read from root to leaf).