Section: New Results
Discontinuous Galerkin methods for Maxwell's equations
DGTD- method based on hierarchical polynomial interpolation
Participants : Loula Fezoui, Stéphane Lanteri.
The DGTD (Discontinuous Galerkin Time Domain) method originally proposed by the team for the solution of the time domain Maxwell's equations [16] relies on an arbitrary high order polynomial interpolation of the component of the electromagnetic field, and its computer implementation makes use of nodal (Lagrange) basis expansions on simplicial elements. The resulting method is often denoted by DGTD- where refers to the interpolation degree that can be defined locally i.e. at the element level. In view of the design of a -adaptive DGTD method, i.e. a solution strategy allowing an automatic adaptation of the interpolation degree and the discretization step , we now investigate alternative polynomial interpolation and in particular those which lead to hierarchical or/and orthogonal basis expansions. Such basis expansions on simplicial elements have been extensively studied in the context of continuous finite element formulations (e.g. [59] ) and have thus been designed with global conformity requirements (i.e. , or ) whose role in the context of a discontinuous Galerkin formulation has to be clarified. This represents one of the objectives of this study. This year, we have started the development of a new software platform in Fortran 95 implementing DGTD- able to deal with different polynomial basis expansions on a tetrahedral element, for the solution of the 3D time domain Maxwell equations.
DGTD- method on multi-element meshes
Participants : Clément Durochat, Stéphane Lanteri, Raphael Léger, Claire Scheid, Mark Loriot [Distene, Pôle Teratec, Bruyères-le-Chatel] .
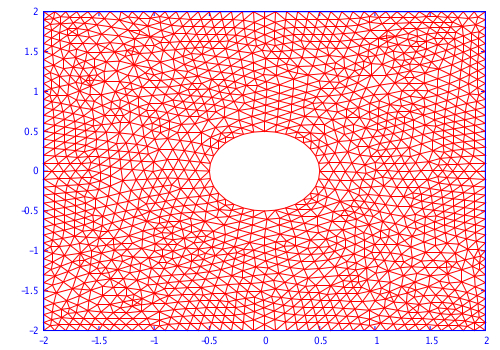
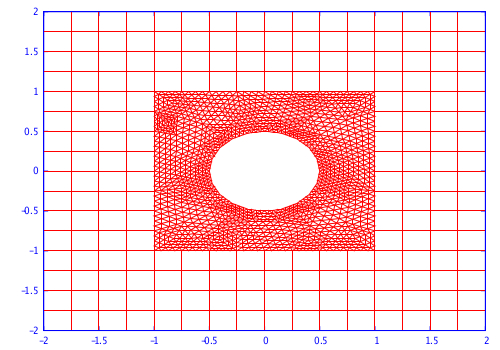
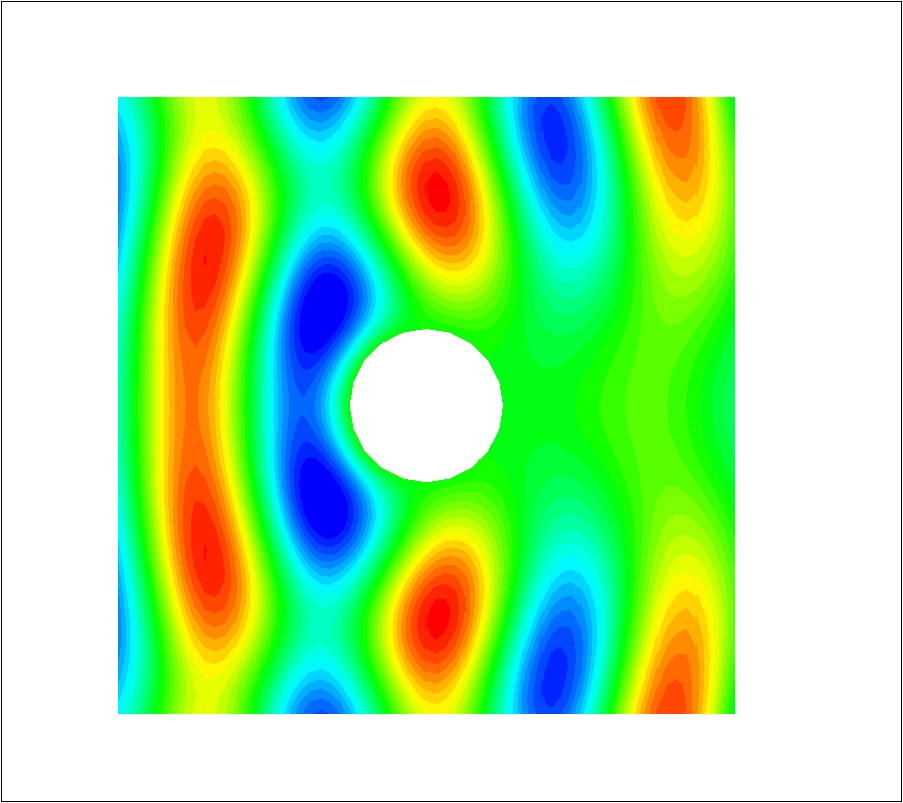
In this work, we study a multi-element DGTD method formulated on a hybrid mesh which combines a structured (orthogonal) discretization of the regular zones of the computational domain with an unstructured discretization of the irregularly shaped objects. The general objective is to enhance the flexibility and the efficiency of DGTD methods for large-scale time domain electromagnetic wave propagation problems with regards to the discretization process of complex propagation scenes. With this objective in mind, we have designed and analyzed a DGTD- method formulated on non-conforming hybrid quadrangular/triangular meshes (2D case) or non-conforming hexahedral/tetrahedral meshes (3D case) for the solution of the time domain Maxwell's equations [23] -[22] .
|
||
|
DGTD- method for Debye media and applications to biolectromagnetics
Participants : Claire Scheid, Maciej Klemm [Communication Systems & Networks Laboratory, Centre for Communications Research, University of Bristol, UK] , Stéphane Lanteri.
This work is undertaken in the context of a collaboration with the Communication Systems & Networks Laboratory, Centre for Communications Research, University of Bristol (UK). This laboratory is studying imaging modalities based on microwaves with applications to dynamic imaging of the brain activity (Dynamic Microwave Imaging) on one hand, and to cancerology (imaging of breast tumors) on the other hand. The design of imaging systems for these applications is extensively based on computer simulation, in particular to assess the performances of the antenna arrays which are at the heart of these systems. In practice, one has to model the propagation of electromagnetic waves emitted from complex sources and which propagate and interact with biological tissues. In relation with these issues, we study the extension of the DGTD- method originally proposed in [16] to the numerical treatment of electromagnetic wave propagation in dispersive media. We consider an approach based on an auxiliary differential equation modeling the time evolution of the electric polarization for a dispersive medium of Debye type (other dispersive media will be considered subsequently). The stability and a priori convergence analysis of the resulting DGTD- method has been studied [25] , and its application to the simulation of the propagation in realistic geometrical models of head tissues is underway in the context of our participation to the DEEP-ER FP7 project.
DGTD- method for nanophotonics
Participants : Claire Scheid, Maciej Klemm [Communication Systems & Networks Laboratory, Centre for Communications Research, University of Bristol, UK] , Stéphane Lanteri, Raphael Léger, Jonathan Viquerat.
Modelling and numerical simulation aspects are crucial for a better understanding of nanophotonics. Media that one encounters are complex and the geometries quite involved, so that while a FDTD method failed to be accurate enough, a non conforming discretisation method seems to be well adapted. In this direction, since the end of 2012, we are actively studying the numerical modeling of electromagnetic wave interaction with nanoscale metallic structures. In this context, one has to take into account the dispersive characteristics of metals in the frequency range of interest to nanophotonics. As a first step in this direction, we have considered an auxiliary differential equation approach for the numerical treatment of a Drude, Drude-Lorentz and a generalized dispersion models in the framework of a DGTD- method [20] -[36] . We performed the corresponding numerical analysis as well as numerical validation tests cases. Some methodological improvements, such as curvilinear elements and higher order time discretization schemes are also underway.
Frequency domain hybridized DGFD- methods
Participants : Stéphane Lanteri, Liang Li [Faculty Member, School of Mathematical Sciences, Institute of Computational Science, University of Electronic Science and Technology of China Chengdu, China] , Ronan Perrussel [Laplace Laboratory, INP/ENSEEIHT/UPS, Toulouse] .
For certain types of problems, a time harmonic evolution can be assumed leading to the formulation of the frequency domain Maxwell equations, and solving these equations may be more efficient than considering the time domain variant. We are studying a high order Discontinuous Galerkin Frequency Domain (DGFD-) method formulated on unstructured meshes for solving the 2D and 3D time harmonic Maxwell equations. However, one major drawback of DG methods is their intrinsic cost due to the very large number of globally coupled degrees of freedom as compared to classical high order conforming finite element methods. Different attempts have been made in the recent past to improve this situation and one promising strategy has been recently proposed by Cockburn et al. [48] in the form of so-called hybridizable DG formulations. The distinctive feature of these methods is that the only globally coupled degrees of freedom are those of an approximation of the solution defined only on the boundaries of the elements. This work is concerned with the study of such Hybridizable Discontinuous Galerkin (HDG) methods for the solution of the system of Maxwell equations in the time domain when the time integration relies on an implicit scheme, or in the frequency domain. We have been one of the first groups to study HDGFD- methods based on nodal interpolation methods for the solution of the 2D and 3D frequency domain Maxwell equations [26] -[27] .
Exact transparent condition in a DGFD- method
Participants : Mohamed El Bouajaji, Nabil Gmati [ENIT-LAMSIN, Tunisia] , Stéphane Lanteri, Jamil Salhi [ENIT-LAMSIN, Tunisia] .
In the numerical treatment of propagation problems theoretically posed in unbounded domains, an artificial boundary is introduced on which an absorbing condition is imposed. For the frequency domain Maxwell equations, one generally use the Silver-Müller condition which is a first order approximation of the exact radiation condition. Then, the accuracy of the numerical treatment greatly depends on the position of the artificial boundary with regards to the scattering object. In this work, we have conducted a preliminary study aiming at improving this situation by using an exact transparent condition in place of the Silver-Müller condition. Promising results have been obtained in the 2D case [30] .