Section: New Results

Time integration strategies and resolution algorithms

Hybrid explicit-implicit DGTD-${\mathbb{P}}_p$ method

Participants : Stéphane Descombes, Stéphane Lanteri, Ludovic Moya.

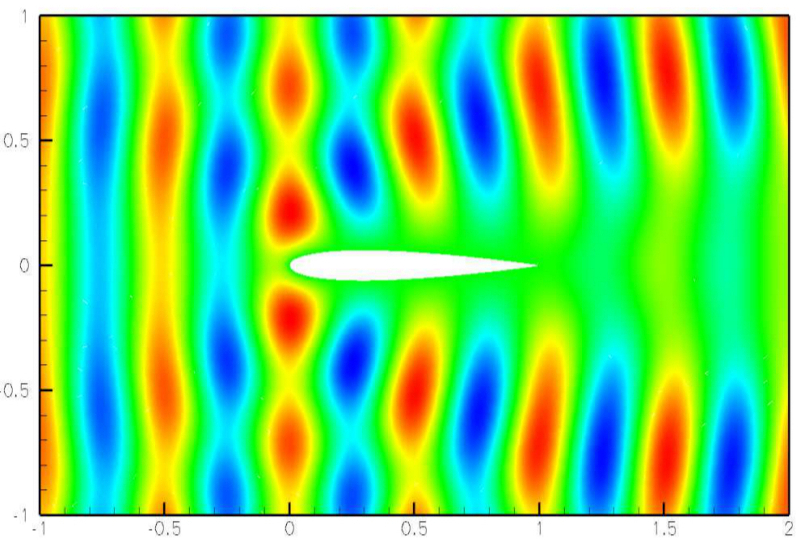
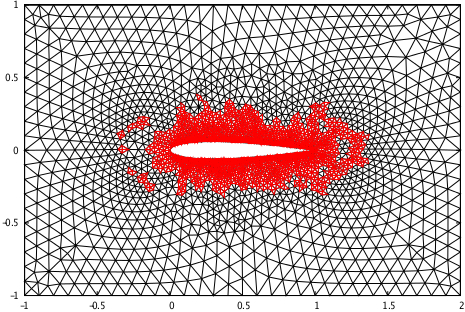
Existing numerical methods for the solution of the time domain Maxwell equations often rely on explicit time integration schemes and are therefore constrained by a stability condition that can be very restrictive on highly refined meshes. An implicit time integration scheme is a natural way to obtain a time domain method which is unconditionally stable. Starting from the explicit, non-dissipative, DGTD-${\mathbb{P}}_p$ method introduced in [16] , we have proposed the use of Crank-Nicolson scheme in place of the explicit leap-frog scheme adopted in this method [5] . As a result, we obtain an unconditionally stable, non-dissipative, implicit DGTD-${\mathbb{P}}_p$ method, but at the expense of the inversion of a global linear system at each time step, thus obliterating one of the attractive features of discontinuous Galerkin formulations. A more viable approach for 3D simulations consists in applying an implicit time integration scheme locally i.e in the refined regions of the mesh, while preserving an explicit time scheme in the complementary part, resulting in an hybrid explicit-implicit (or locally implicit) time integration strategy. In [7] , we conducted a preliminary numerical study of a hyrbid explicit-implicit DGTD-${\mathbb{P}}_p$ method, combining a leap-frog scheme and a Crank-Nicolson scheme, and obtained promising results. More recently, we further investigated two such strategies, both theoretically (especially, convergence in the ODE and PDE senses) [17] and numerically in the 2D case [28] . A last topic is to propose higher order time integration techniques based on the second-order locally implicit method to fully exploit the attractive features of this approach combined with a DG discretisation which allows to easily increase the spatial convergence order. Promising results in 2D reaching high order in time, between $3,5$ and 4, have been obtained in [29] by applying Richardson extrapolation and composition methods.

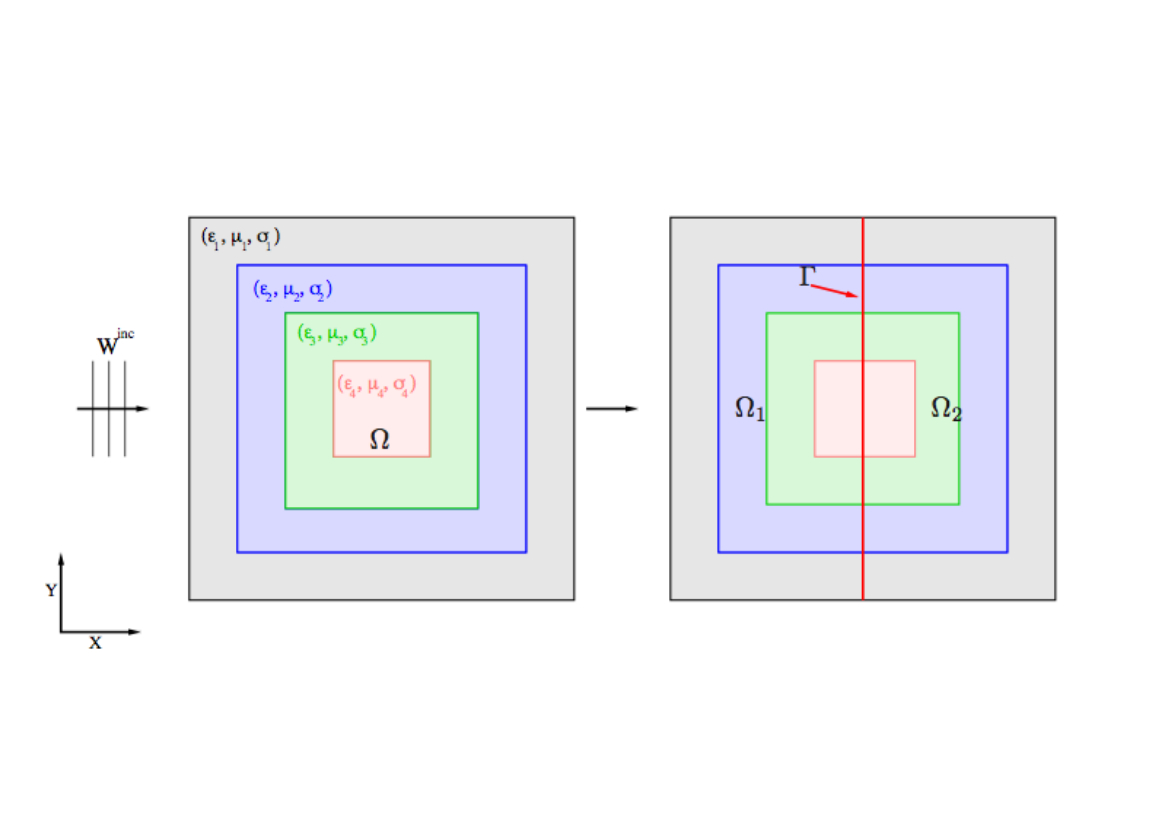
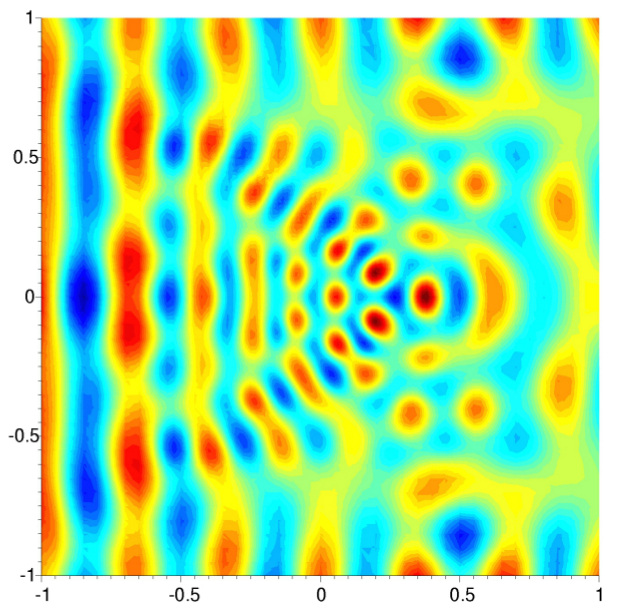
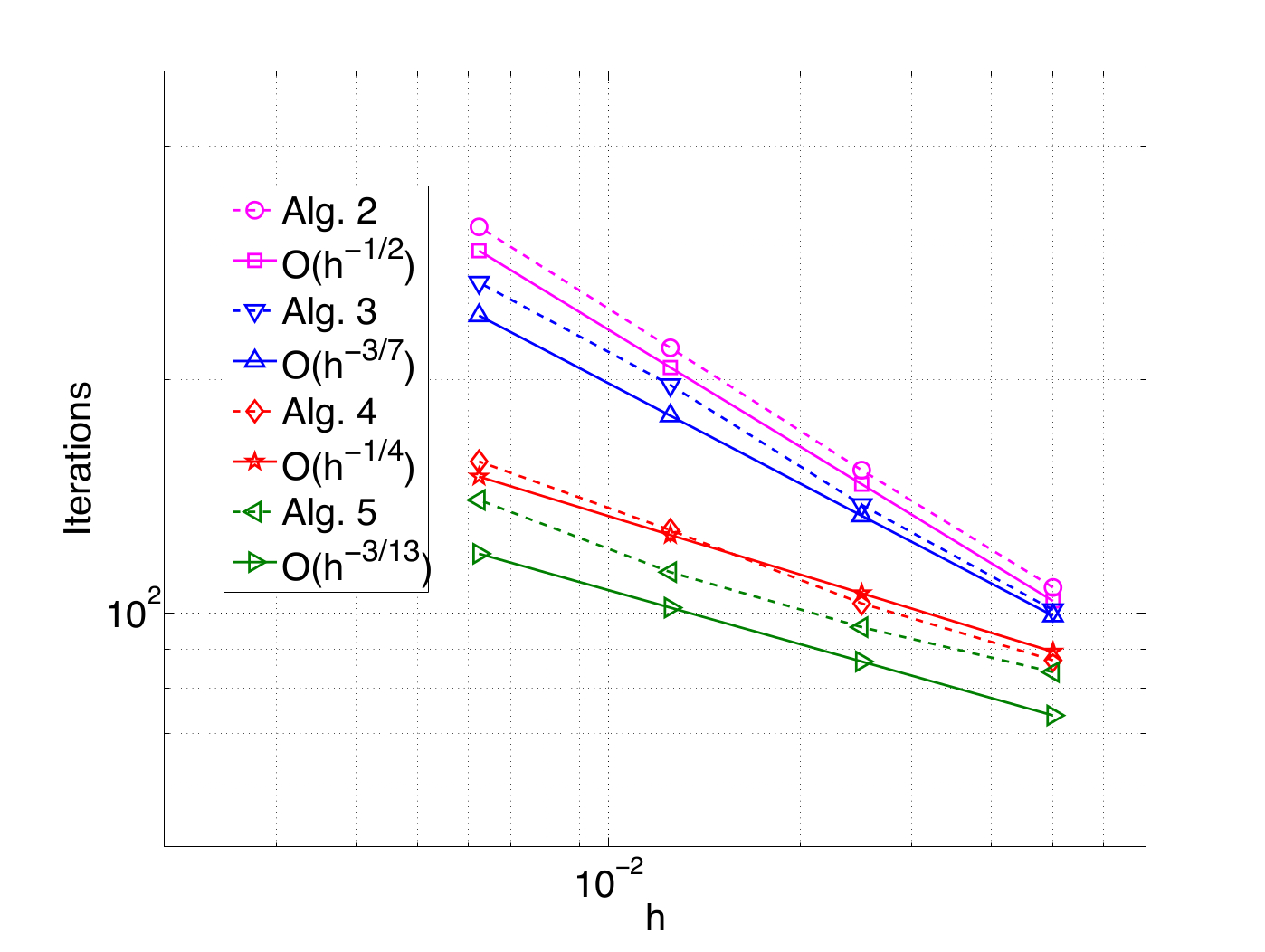
Optimized Schwarz algorithms for the frequency domain Maxwell equations

Participants : Victorita Dolean, Martin Gander [Mathematics Section, University of Geneva] , Stéphane Lanteri, Ronan Perrussel [Laplace Laboratory, INP/ENSEEIHT/UPS, Toulouse] .

Even if they have been introduced for the first time two centuries ago, over the last two decades, classical Schwarz methods have regained a lot of popularity with the developement of parallel computers. First developed for the elliptic problems, they have been recently extended to systems of hyperbolic partial differential equations, and it was observed that the classical Schwartz method can be convergent even without overlap in certain cases. This is in strong contrast to the behavior of classical Schwarz methods applied to elliptic problems, for which overlap is essential for convergence. Over the last decade, optimized versions of Schwarz methods have been developed for elliptic partial differential equations. These methods use more effective transmission conditions between subdomains, and are also convergent without overlap for elliptic problems. The extension of such methods to systems of equations and more precisely to Maxwell's system (time harmonic and time discretized equations) has been studied in [9] . The optimized interface conditions proposed in [9] were devised for the case of non-conducting propagation media. We have recently studied the formulation of such conditions for conducting media [4] . Besides, we have also proposed an appropriate discretization strategy of these optimized Schwarz algorithms in the context of a high order DGFD-${\mathbb{P}}_p$ method formulated on unstructured triangular meshes for the solution of the 2D frequency domain Maxwell equations [42] .