Accessibility setting

Section: New Results

Source recovery problems

Participants : Laurent Baratchart, Sylvain Chevillard, Juliette Leblond, Christos Papageorgakis, Olga Permiakova, Dmitry Ponomarev.

The research in this section is partly joint work with Qian Tao (Univ. Macao).

It was proved in [38] that a vector field with $n+1$ components on ${ℝ}^n$ can be expressed uniquely as the sum of (the trace on ${ℝ}^n$ of) a harmonic gradient in the upper half-space, of (the trace on ${ℝ}^n$ of) a harmonic gradient in the lower half-space, and of a tangential divergence free vector field on ${ℝ}^n$. This decomposition, that we call the Hardy-Hodge decomposition, is valid not only for $L^p$ vector fields as mentioned in Section  3.3.1 , but in much more general distribution spaces like $W^{-\infty ,p}$ which contains all distributions with compact support or $BM{O}^{-\infty }$ which contains all finite sums of derivatives of bounded functions. This year we extended the decomposition to smooth hypersurfaces, where divergence-free distributions may be defined as those annihilating tangential gradient vector fields. We also studied the case where the hypersurface is only Lipschitz smooth, and then we proved the decomposition in $L^p$ provided that $p$ is close enough to 2 (how close depends on the Lipschitz constant of the hypersurface).

The Hardy-Hodge decomposition was used in [38] to find the kernel of the planar magnetization operator, namely a potential of the form (1 ) with $m$ supported in a plane generates the zero field above that plane if, and only if there is no harmonic gradient from below in the Hardy-Hodge decomposition of $m$. The above mentioned generalization is now to the effect that a magnetization supported on a bounded closed surface (e.g. a sphere) is silent in the unbounded component of the complement of that surface if, and only if there is no harmonic gradient from inside in its Hardy-Hodge decomposition. An article is being written on this topic.

We also considered the case where $m$ is compactly supported in the bounded component of the complement of that surface. Then $m$ is silent if and only if it is the sum of a divergence-free distribution and of finitely many derivatives of gradients of Sobolev functions having zero trace on the surface [41] .

These results shed light on the indeterminacy of inverse source problems.

EEG

This work is conducted in collaboration with Maureen Clerc and Théo Papadopoulo from the Athena EPI, and with Jean-Paul Marmorat (Centre de mathématiques appliquées - CMA, École des Mines de Paris).

In 3-D, functional or clinically active regions in the cortex are often modeled by point-wise sources that must be localized from measurements of a potential on the scalp. Inside the cortex, identified to a ball after the cortical mapping step, the potential satisfies a Poisson equation whose right-hand side is a linear combination of gradients of Dirac masses (the sources in EEG). In the work [3] it was shown how best rational approximation on a family of circles, cut along parallel planes on the sphere, can be used to recover the sources when they are at most 2 of them. Later, results on the behavior of poles in best rational approximation of fixed degree to functions with branch points [6] helped justifying the technique for finitely many sources (see section 4.2 ).

The dedicated software FindSources3D (see section 5.6 ), developed, in collaboration with the team Athena and the CMA, dwells on these ideas. Functions to be approximated in 2-D slices turn out to have additional multiple poles at their branch points so that, in the rational approximation step, it is beneficial to consider approximants with multiple poles as well (for EEG data, one should consider triple poles). Though numerically observed in [9] , there is no mathematical justification so far why these multiple poles are attracted more strongly than simple poles to the singularities of the approximated function. This intriguing property, however, definitely helps source recovery [28] . This year we used it to automatically estimate the “most plausible” number of sources (numerically: up to 3 at the moment). Such enhancements were prompted by a developing collaboration with the BESA company, which is interested in automatic detection of the number of sources (which was left to the user until recently).

Soon, magnetic data from MEG (magneto-encephalography) will become available together with EEG data; indeed, it is now possible to use simultaneously the corresponding measurement devices. We expect this to improve the accuracy of our algorithms.

In relation to other brain exploration modalities like electrical impedance tomography (EIT, see [16] ), we also consider identifying electrical conductivity in the head. This is the topic of the PhD of C. Papageorgakis, co-advised with the Athena project-team and BESA GmbH. Specifically, in layered models, we are concerned with estimating conductivity of the skull (intermediate layer). Indeed, the skull consists of a hard bone part, the conductivity of which is more or less known, and spongy bone compartments whose conductivities may vary considerably with individuals.

A preliminary question in this connection is: can one uniquely recover a homogeneous skull conductivity from a single EEG recording when the sources and the conductivities of other layers are known? And if sources are not known, which additional information do we need? These are issues currently under investigation. To put them into perspective, recall the famous Caldèron problem of deducing a bounded (nonconstant) conductivity from the knowledge of all possible pairs consisting of a potential and its current flux at the boundary. In dimension 3, when the conductivity is not smooth (less than $3/2$ of a derivative), it is unknown whether the problem is even injective (i.e. if two conductivities can have the same pairs of boundary potential and flux). A weaker, discrete version of this problem is: if the conductivity takes on finitely many values and the geometry of the level sets is known, does a finite set of pairs of boundary potential and flux allow one to recover it? This is a significant question to be tackled for the purpose of source recovery in EEG with known geometry but unknown conductivities inside the head.

Inverse Magnetization problems

This work is carried out in the framework of the “équipe associée Inria” IMPINGE, comprising Eduardo Andrade Lima and Benjamin Weiss from the Earth Sciences department at MIT (Boston, USA) and Douglas Hardin and Edward Saff from the Mathematics department at Vanderbilt University (Nashville, USA),

Localizing magnetic sources from measurements of the magnetic field away from the support of the magnetization is the fundamental issue under investigation by IMPINGE. The goal is to determine magnetic properties of rock samples (e.g. meteorites or stalactites), from fine field measurements close to the sample that can nowadays be obtained using SQUIDs (superconducting coil devices). Currently, rock samples are cut into thin slabs and the magnetization distribution is considered to lie in a plane, which makes for a somewhat less indeterminate framework than EEG because “less” magnetizations can produce the same field (for the slab has no inner volume). Note however that EEG data consist of both potential and current values at the boundary, whereas in the present setting only values of the normal magnetic field are provided to us.

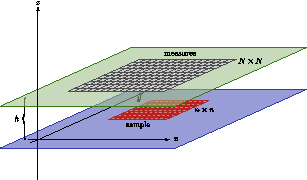
Figure 5 presents a schematic view of the experimental setup: the sample lie on a horizontal plane at height 0 and its support is included in a rectangle. The vertical component $B_z$ of the field produced by the sample is measured on points of a horizontal $N\times N$ rectangular grid at height $h$.

We set up last year a heuristic procedure to recover regularly spaced dipolar magnetizations, i.e. magnetizations composed of dipoles placed at the points of a regular rectangular $n\times n$ grid. The latter seems general enough a model class to approximate magnetizations commonly encountered in samples. However, for reasons of computational complexity, $n$ is significantly smaller than $N$ which limits the power of the model. Each dipole of the $n\times n$ grid is determined by the 3 components of its moment, thus the magnetization can be represented by a real $3n^2$-vector. If we denote by $A$ the matrix of the operator that maps such a vector $X$ to the vector $b$ of measurements (which belongs to ${ℝ}^{N^2}$), we want to find $X$ such that $AX$ is close to $b$. For computational simplicity, we use a Euclidean criterion ${\parallel AX-b\parallel }_2$, which reduces the problem to a singular value decomposition of $A$. The inverse problem being ill-posed, $A$ is poorly conditioned and we must resort to a regularization technique. The one we developed initially has been based on iteratively cropping the support of $b$, using a threshold on the intensity of the dipoles at each step, so as to reduce the number of active components in $b$. Preliminary experiments were performed last year on synthetic data and also on a real example (Lonar spherule).

This year, we performed more systematic experiments on real data (namely Allende chondrules and Hawaian basalt) provided by the SQUID scanning microscope at MIT lab. Cropping the support of $b$ using thresholding has proved efficient to improve ill-conditioning for samples with localized support embedded in the slab (e.g., chondrules). On the other hand, when the support of the sample is spread out (e.g., Hawaian basalt), the reduction of active components of $b$ was insignificant. We used this inversion procedure to estimate the net moment. The importance of the latter has been emphasized by the geophysicists at MIT for at least two reasons: firstly it yields important geological information on the sample in particular to estimate the magnitude of the ambient magnetic field at the time the rock was formed. Secondly, it may to some extent be measured independently, using a magnetometer, thereby allowing one to cross-validate the approach. A third, computational reason is that knowledge of the net moment should pave the way to a numerically stable reconstruction of an equivalent unidirectional magnetization. The support of the latter would provide us with valuable information to test for unidirectionality of the true magnetization, which is an important question to physicists.

When the support can be significantly shrunk while keeping the residue small (i.e., explaining the data satisfactorily), estimates of the net moment based on the dipolar model obtained by inversion seem to be good. They apparently supersede the measurements by magnetometers as well as by dipole fitting procedures set up at MIT. It is interesting to notice that the magnetization obtained by our inversion procedure, either before or after shrinking the support, often does not resemble the true magnetization, even when it yields correct moment and field. This can be seen on synthetic examples and may be surmised on real data, thereby confirming that recovering the net moment and recovering the magnetization are rather different problems, the latter being considerably more ill-posed than the former.

One specific difficulty with chondrule-type examples has been to account for their thickness: they are indeed small spheres and their 3-D character cannot be completely ignored. In order to use the inversion procedure set up in the plane, we investigated the following question. Assume that the sample has some thickness, but small enough that the magnetization at a point $P=(x,y,z)$ inside the sample depends only on $x$ and $y$ (possibly weighted by some function that depends only on $z$), i.e. that it is of the form $m(x,y)\phi \left(z\right)$. If we consider a (truly) planar magnetization with the same distribution $m(x,y)$ but on a plane lying at some nonzero height $\epsilon$, how to choose $\epsilon$ so as to produce a field at height $h$ which is closest to the field produced by the thick magnetization? This has been the object of the internship of Olga Permiakova who used local expansion of the dipole-to-field map (see her report (http://www-sop.inria.fr/apics/IMPINGE/Documents/Report_Permiakova_Olga.pdf )). An article is being written on this subject.

The case where the magnetization is flat but spread out on the sample is more difficult. First of all, the computational effort becomes significant and led us to use the cluster at Inria Sophia Antipolis. We succeeded in obtaining full inversions for the Hawaian basalt. The residue (approximation error) is moderate but not impressively small, which indicates that we reach the limit of modeling magnetizations by a regular grid of dipoles. However the computation of the moment compares favorably with estimates previously obtained by a different technique at MIT lab. Still, using a cluster and two days of evaluation to obtain a coarse estimate of the net moment of a sample is rather inefficient and calls for new investigations.

We also experimented an alternative regularization procedure, based on $L^2$ minimization under $L^1$ penalty as solved by the SALSA algorithm. Such methods are quite popular today for sparse recovery. However, the computational load, as well as the quality of the results, do not differ significantly from those obtained previously.

We now develop new methods in order to estimate the net moment of the magnetization, based on improvements of previously used Fourier techniques, and recently we reformulated the problem with the help of Kelvin transforms. It has been realized that the success of net moment recovery hinges on the ability to extrapolate the measurements. In particular, we managed to considerably improve previous estimates by means of data extension based on dipolar field asymptotics.

In the course of inverting the field map, we singled out magnetizations which are numerically (almost) silent from above though not from below. This illustrates how ill-posed (unstable) the problem, as theory predicts that no compactly supported magnetization can be exactly silent from above without being also exactly silent from below. Although such magnetizations seem to have small moment and therefore do not endanger the possibility of recovering the net moment, their existence is certainly an obstacle to inversion of the field map without extra measurements or hypotheses (e.g., measuring from below or assuming unidirectionality).

In the course of the doctoral work by D. Ponomarev, the study of the 2D spectral decomposition of the truncated Poisson operator has been undertaken. It is a simplified version of the relation between the magnetization and the magnetic potential. We considered several formulations in terms of singular integral equations and matrix Riemann-Hilbert problems, and focused on finding closed form solutions for various approximations of the Poisson operator in terms of a the ratio between the distance $h$ to the measurement plane and the sample support size.

Lately, Apics became a partner of the ANR project MagLune, dealing with Lunar magnetism, a in collaboration with the Geophysics and Planetology Department of Cerege, CNRS, Aix-en-Provence, see section 8.2.2 . The research is just starting, and will focus on computing net moments of lunar rock samples collected by NASA.