Accessibility setting

Section: New Results

Matching problems and their applications - De-embedding of filters in multiplexers

Participants : Laurent Baratchart, Martine Olivi, Sanda Lefteriu, David Martinez Martinez, Fabien Seyfert.

This work has been done in collaboration with Stéphane Bila (Xlim, Limoges, France), Hussein Ezzedin (Xlim, Limoges, France), Damien Pacaud (Thales Alenia Space, Toulouse, France), Giuseppe Macchiarella (Politecnico di Milano, Milan, Italy), and Matteo Oldoni (Siae Microelettronica, Milan, Italy).

Matching problems and their applications

Filter synthesis is usually performed under the hypothesis that both ports of the filter are loaded on a constant resistive load (usually 50 Ohm). In complex systems, filters are however cascaded with other devices, and end up being loaded, at least at one port, on a non purely resistive frequency varying load. This is for example the case when synthesizing a multiplexer: each filter is here loaded at one of its ports on a common junction. Thus, the load is by construction non constant with the frequency, and not purely resistive either. Likewise, in an emitter-receiver, the antenna is followed by a filter. Whereas the antenna can usually be regarded as a resistive load at some frequencies, this is far from being true on the whole working band. A mismatch between the antenna and the filter, however, causes irremediable power losses, both in emission and transmission. Our goal is therefore to develop a filter synthesis method that allows to match varying loads on specific frequency bands.

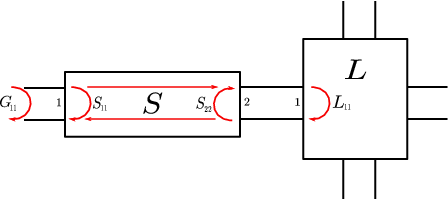
Figure 6 shows a filter with scattering matrix $S$, plugged at its right port on a frequency varying load with reflexion parameter $L_{1,1}$. If the filter is lossless, simple algebraic manipulations show that on the frequency axis the reflexion parameter satisfies:

The matching problem of minimizing $|G_{1,1}|$ amounts therefore to minimize the pseudo-hyperbolic distance between the filter's reflexion parameter $S_{2,2}$ and the load's reflexion $L_{1,1}$, on a given frequency band. For a broad class of filters, namely those that can be modeled by a circuit of $n$ coupled resonators, the scattering matrix $S$ is a rational function of McMillan degree $n$ in the frequency. The matching problem appears therefore as a rational approximation problem in hyperbolic metric. When $n$ is fixed, the latter is non-convex and led us to seek methods to derive good initial guesses for classical descent algorithms. To this effect, if $S_{2,2}=p/q$ we considered the following interpolation problem: given $n$ frequency points $w_1\cdots w_n$ and a transmission polynomial $r$, to find a unitary polynomial $p$ of degree $n$ such that:

where $q$ is the unique monic Hurwitz polynomial of degree $n$ satisfying the Feldtkeller equation

which accounts for the losslessness of the filter. This problem can be seen as an extended Nevanlinna-Pick interpolation problem, that was considered in [67] when the interpolation points $w_j$ lie in the open left half-plane. The method in the last reference does not extend to imaginary interpolation point and we used rather different, differential-topological techniques to prove that this problem has a unique solution, which can be computed by continuation. In the setting of multiplexer synthesis, where this result must e applied recursively to each filter, we showed the existence of a fixed point for the tuning procedure, based on Brouwer's fixed point theorem. These results were presented at the MTNS [18] , at the plenary of session of Ernsi workshop 2014, and they lie at the heart of the ANR Cocoram on co-integration of filters and antennas ( 8.2.1 ). Implementation of the continuation algorithm has been done under contract with CNES and yields encouraging results. Generalizations of the interpolation problem where the monic condition is relaxed are under study in the framework of co-integration of filters and antennas.

De-embedding of multiplexers

This work is pursued in collaboration with Thales Alenia Space, Siae Microelettronica, Xlim and under contract with CNES-Toulouse (see section 7.1 ).

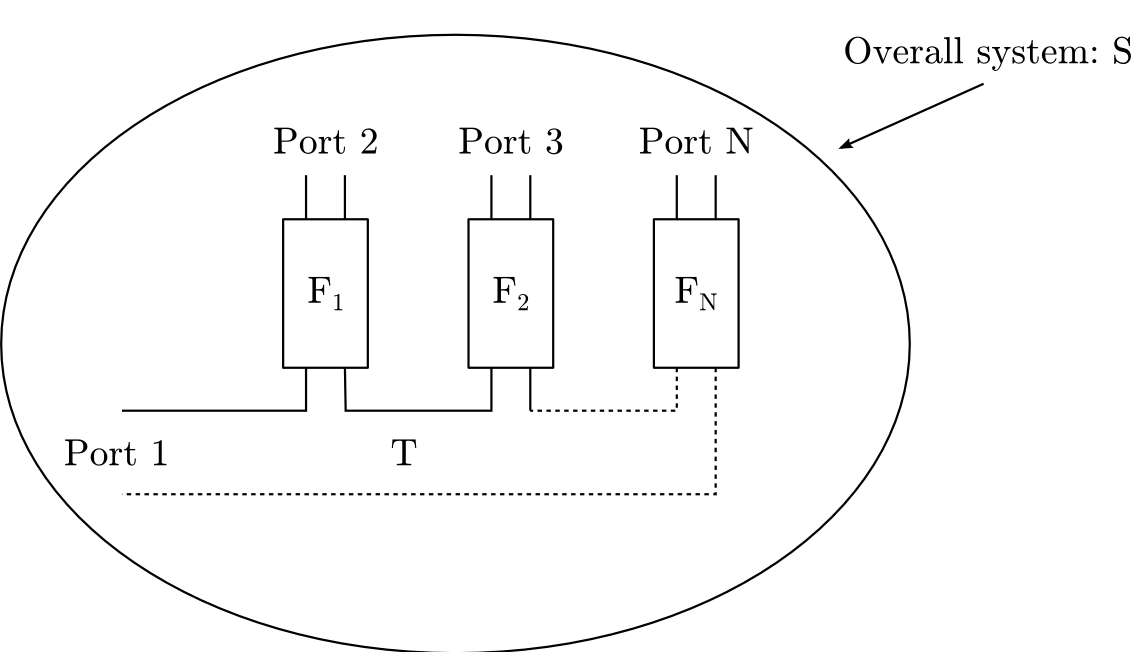
Let $S$ be the scattering parameters of a multiplexer composed of a $N$-port junction with response $T$ and $N-1$ filters with responses $F_1,\cdots F_{N-1}$, as plotted on Figure 7 . The de-embedding problem is to recover the $F_k$ and it can be stated under various hypotheses. Last year we studied this problem when $S$ and $T$ are known [79] but no special structure for the $F_k$ is assumed. It was shown that for generic $T$ and for $N>3$, the de-embedding problem has a unique solution. In practice, however, the junction's response is far from being generic, as it is usually obtained via assembly of T-junctions. This makes the problem extremely sensitive to measurement noise. It was also noticed that in practical applications, scattering measurements of the junction are hardly available.

It is therefore natural to consider the following de-embedding problem. Given $S$, and under the assumption that

• the $F_k$ are rational of known McMillan degree,

• the coupling geometry of their circuital realization is known,

what can be said about the filter's response? Note that the above assumptions do not bear on the junction. Nevertheless, we showed that the filter's responses are identifiable up to a constant matrix chained at their nearest port to the junction [73] . It was proved also that the uncertainty induced by the chain matrix bears only on the resonant frequency of the last cavity of each filter, as well as on their output coupling. Most of the filters' parameters can therefore be recovered in principle. The approach is constructive and relies on rational approximation to certain scattering parameters, as well as on some extraction procedure similar to Darlington's synthesis. Software development is under way and experimental studies have started on data provided to us by Thales Alenia Space and by Siae Microelettronica. A mid-term objective is to extend Presto-HF (see Section  5.3 ) so as to handle de-embedding problems for multiplexers and more generally for multi-ports.